Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
14.4. Проекции плоскости. Плоскость в проекциях с числовыми отметками может быть задана всеми известными в начертательной геометрии способами. Но часто плоскость задается масштабом уклонов (рис. 103 а, б). Такое задание является наиболее наглядным и удобным при решении инженерных задач. Проекции горизонталей плоскости и масштаб уклонов пересекаются под прямым углом. Интервал плоскости равен интервалу ее линии ската. Линия ската плоскости иначе называется линией падения. Она определяет угол наклона или угол падения плоскости (рис. 103а). 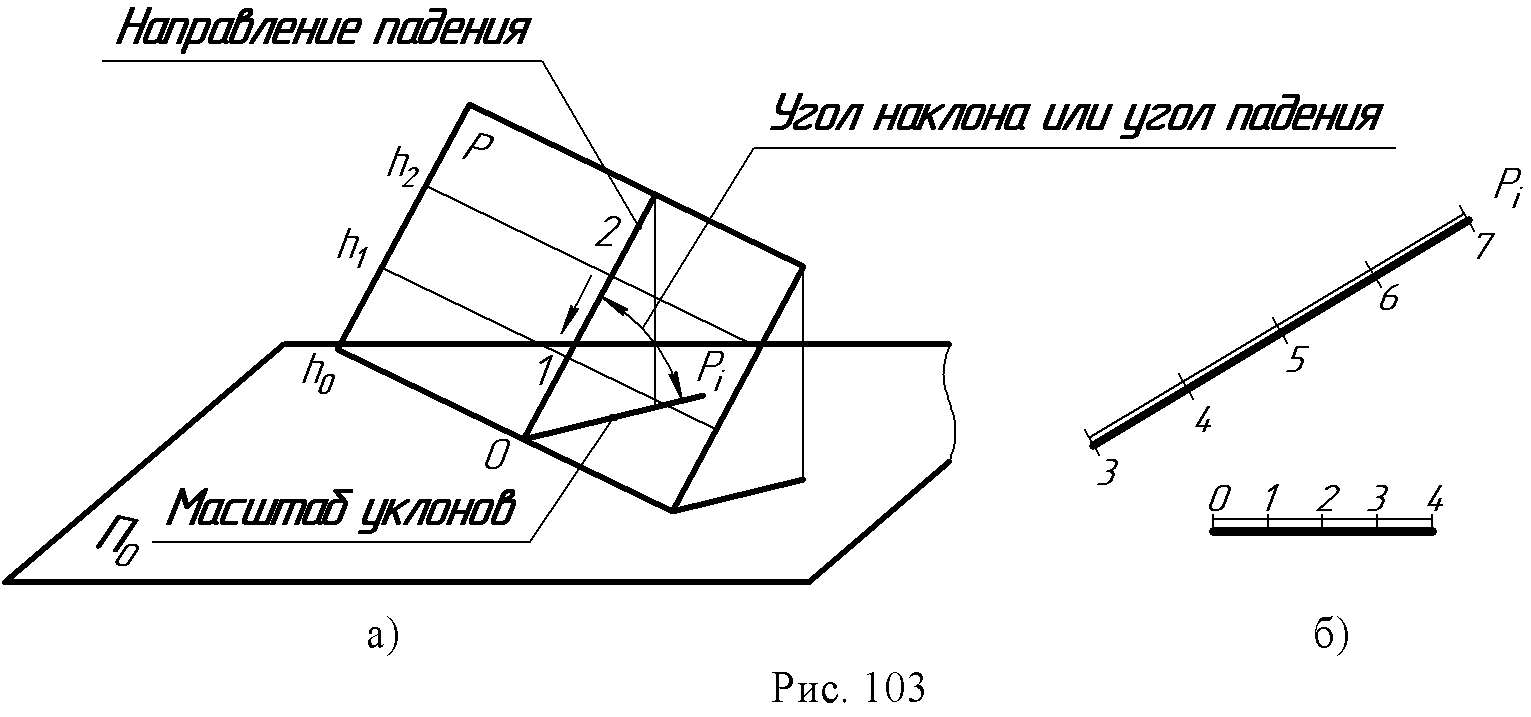 Масштабом уклонов называют проградуированную проекцию линии ската плоскости. Масштаб уклонов изображается на плане двумя параллельными прямыми: толстой и тонкой с нанесенными на ней отметками горизонталей плоскости (рис. 103б). Направление и угол простирания. При проведении проектно – изыскательских и геологических работ возникает необходимость определять положение плоскости относительно сторон света. Это положение определяется такими понятиями как направление простирания и угол простирания. За направление простирания плоскости принимается направление вправо по горизонталям, если смотреть на масштаб уклона плоскости в сторону возрастания отметок (рис. 103 а, в). Углом простирания плоскости называется угол между северным концом меридиана и направлением простирания против хода часовой стрелки (рис. 103в). 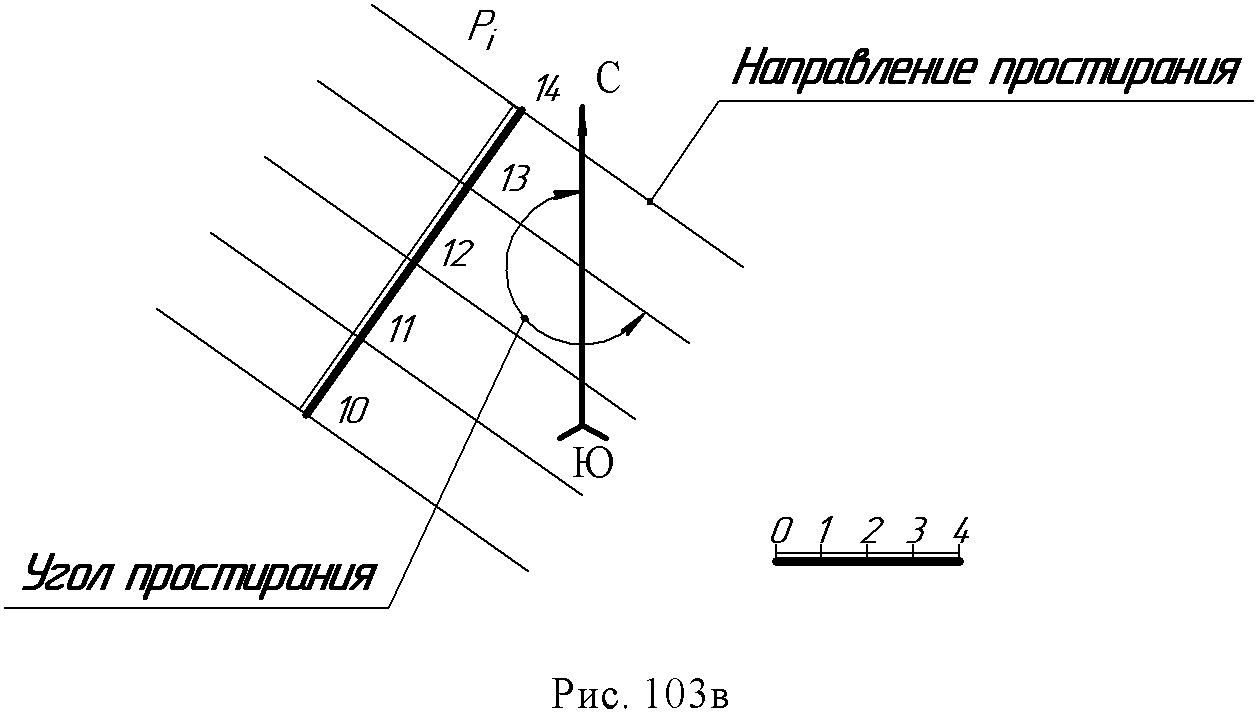 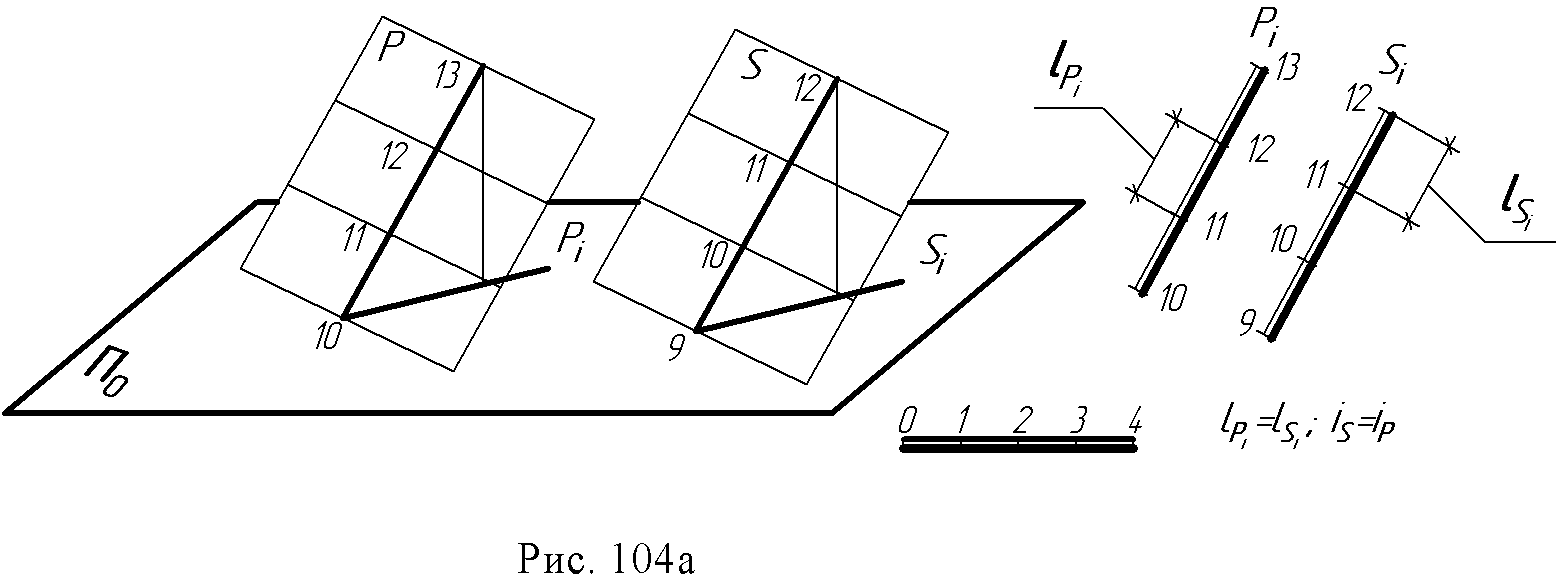 14.5. Взаимное положение плоскостей Если плоскости параллельны, параллельны их масштабы уклонов, интервалы и уклоны равны, отметки возрастают в одну сторону (рис. 104а). Плоскости пересекающиеся Если хотя бы один из признаков параллельности плоскостей отсутствует, плоскости пересекаются. Линии пересечения находятся на основе метода секущих плоскостей – посредников. Решение задачи сводится к нахождению точек пересечения двух пар горизонталей с одинаковыми отметками (рис. 104б). 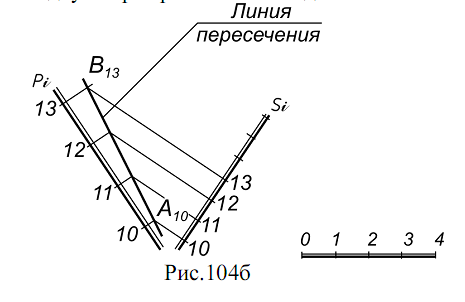 14.6. Точка, прямая и плоскость. Пересечение прямой и плоскости. Для нахождения точки пересечения прямой АВ с плоскостью аiчерез данную прямую проводится вспомогательная плоскость β которую можно задать параллельными прямыми, т.е. горизонталями произвольного направления А8N8 и B6M6. Точки пересечения М6и N8этих горизонталей с однозначными горизонталями плоскости аопределяют линию пересечения двух плоскостей (заданной аи вспомогательной β ). Точка К пересечения этой линии MN с данной прямой АВ - искомая (рис. 105а). 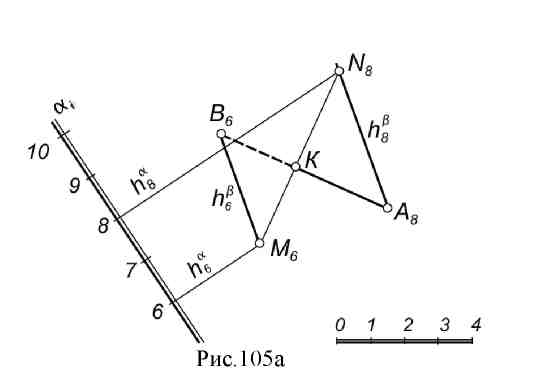 Инцидентность (принадлежность) точки, прямой и плоскости. Задачи на взаимную принадлежность точки, прямой и плоскости решаются обычными методами. Прямая в плоскости строится по двум точкам, отметки которых определяются в местах пересечения проекции прямой с горизонталями плоскости. Точка в плоскости строится с помощью произвольной прямой, проходящей через точку. Для определения отметки точки прямая градуируется (рис. 105б). 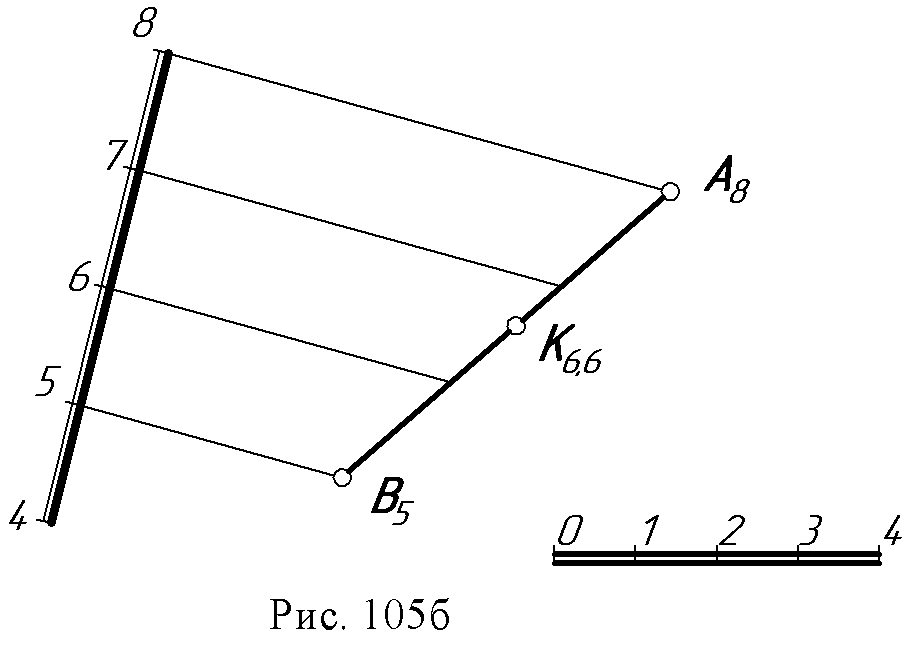 14.7. Вопросы для самопроверки
15. Лекция 15. Проекции с числовыми отметками. 15.1. Поверхности в проекциях с числовыми отметками В проекциях с числовыми отметками форма любых поверхностей достаточно полно характеризуется их горизонталями. Пирамиды Пирамиды можно задать проекциями ребер с указанием отметок вершин (рис. 106а). Точки А, В, С имеют отметки ноль, следовательно, основание пирамиды лежит на нулевой плоскости П0, Произведя градуирование проекций ребер, например, AS можно провести проекции горизонталей 1 и 2 плоскости грани ASB, соединив прямыми линиями точки, имеющие одинаковые отметки. 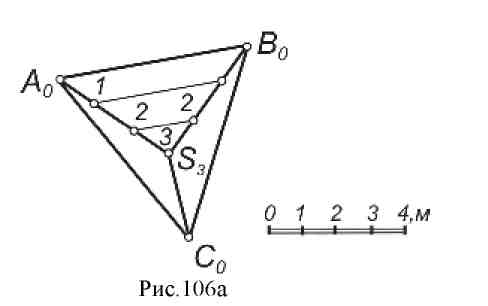 Кривые поверхности Конус. Прямой круговой конус (рис. 106б) как поверхность равного наклона изображается серией концентрических окружностей, проведенных через равные интервалы. 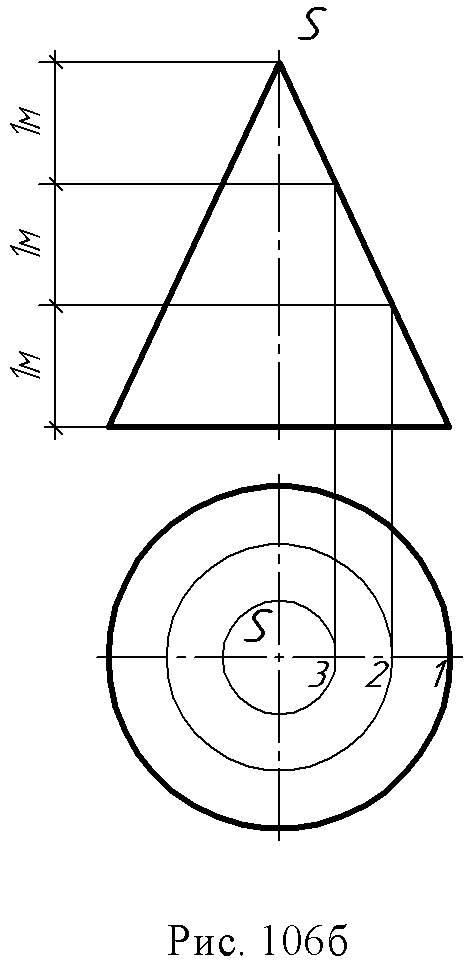 Поверхность равного уклона. Это линейчатая поверхность, все прямолинейные образующие которой составляют с горизонтальной плоскостью постоянный угол (рис. 107а). Такая поверхность может быть образована, если прямой круговой конус с вертикальной осью и образующими заданного уклона перемещать вдоль некоторой направляющей кривой, оставляя ось конуса вертикальной. Поверхность, огибающая конусы во всех положениях, и будет поверхностью равного уклона (рис. 107а). 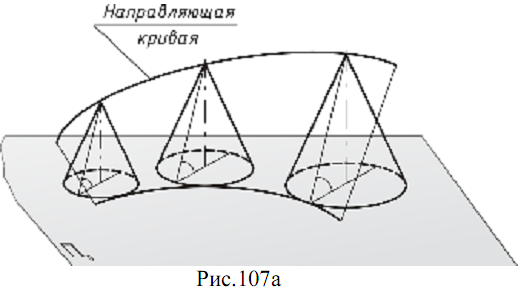 Поверхности откосов насыпей и выемок на криволинейных участках дорог являются поверхностями равного уклона (рис. 107б). 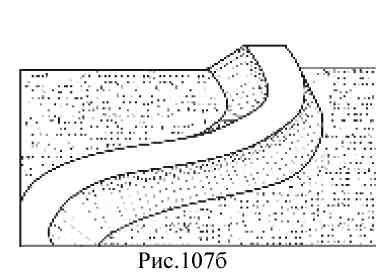 На рис. 107в показано построение проекций горизонталей этой поверхности. Вершина конуса перемещается по градуированной криволинейной направляющей. Из точек деления направляющей, как из центров, проводят концентрические дуги – горизонтали с постоянным интервалом между ними. Строят семейство линий касательно огибающих горизонтали конусов, имеющие одинаковые отметки. Эти линии являются горизонталями поверхности равного уклона. Линии пересечения любой поверхности горизонтальными плоскостями принято называть горизонталями поверхности. 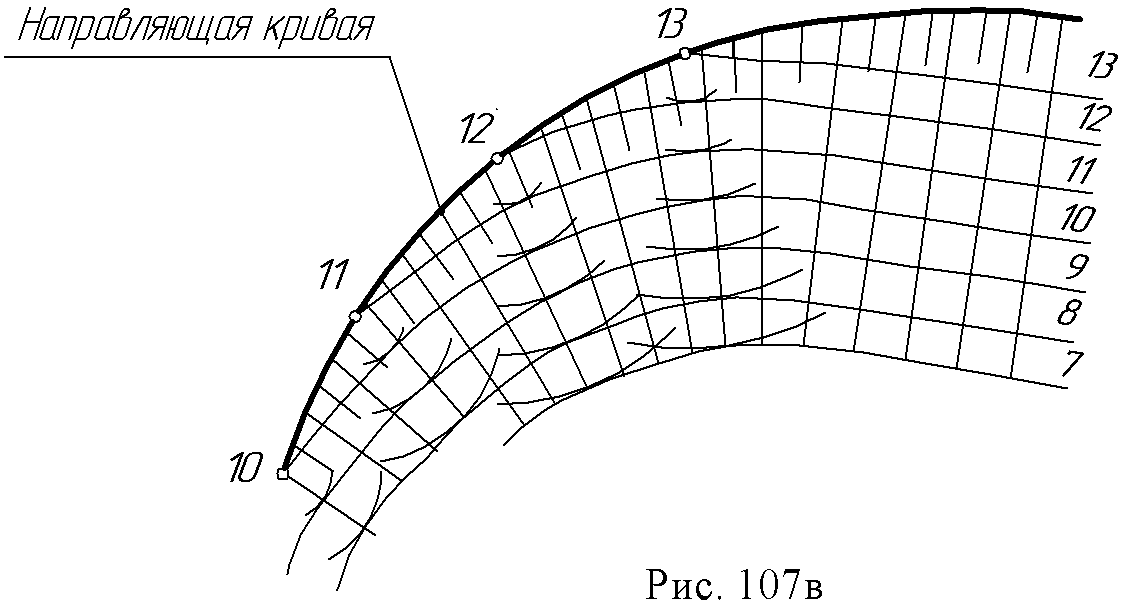 Кривые поверхности задаются проекциями горизонталей (случайного вида) поверхностей, так называемых графических или в применении к земной поверхности – топографических. На рис. 108 при помощи горизонталей изображена котловина, на что указывают форма и отметки горизонталей. 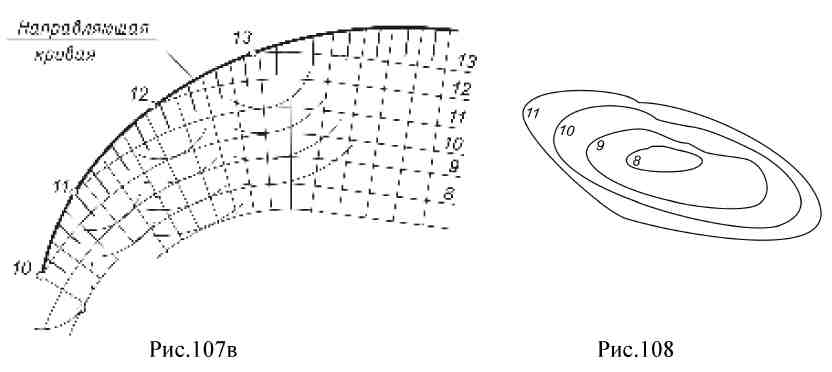 Рис. 108 15.2. Позиционные задачи в проекциях с числовыми отметками. Пересечение поверхности плоскостью Построение линии пересечения поверхности с плоскостью основано на общем для всех типов проекций методе вспомогательных секущих плоскостей. Порядок построения линии пересечения поверхности плоскостью (алгоритм):
Пример (рис. 109). Котлован под сооружение представляет собой усеченную четырехгранную пирамиду, боковые грани которой имеют уклон 2:1. Дно котлована - горизонтальная площадка с отметкой 4. Построить линию пересечения боковых граней (откосов) котлована с наклонной поверхностью земли (плоскостью α), заданной масштабом уклона αi. Решение 1. Перпендикулярно к границам дна котлована как к горизонталям будущих откосов проведем линии масштабов уклонов плоскостей, образующих откосы. Для градуирования этих масштабов вычислим интервал l = 1 / i= 0,5м. Взяв по масштабу чертежа отрезок l=0,5м, последовательно отложим его на линиях масштабов уклонов. Полученные точки обозначим отметками 4, 5, 6 и т.д. (по необходимости).
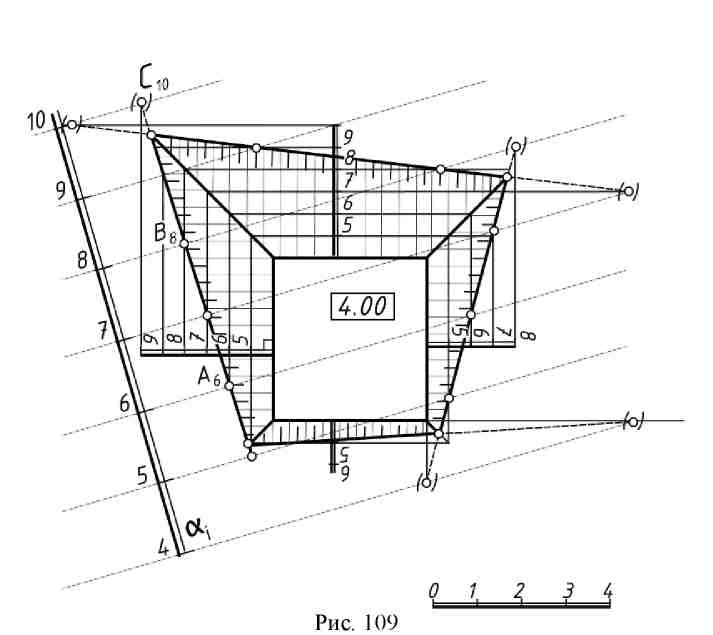 Взаимное пересечение поверхностей. Любая поверхность в проекциях с числовыми отметками определяется семейством горизонталей, которые представляют собой результат сечения поверхности плоскостями уровня. Линия пересечения поверхностей находится как геометрическое место точек пересечения горизонталей с одинаковыми отметками, принадлежащих каждой из пересекающихся поверхностей. Рассмотрим примеры. Пример 1 (рис. 110) Определить границы насыпей и выемок горизонтальной строительной площадки и аппарели (аппарель - пологий въезд или спуск на горизонтальную площадку), с уклоном ia=1 : 3, расположенных на плоском склоне, заданном горизонталями. Уклоны откосов насыпи iH=2 : 3, уклоны откосов выемки iВ=1:1. Решение
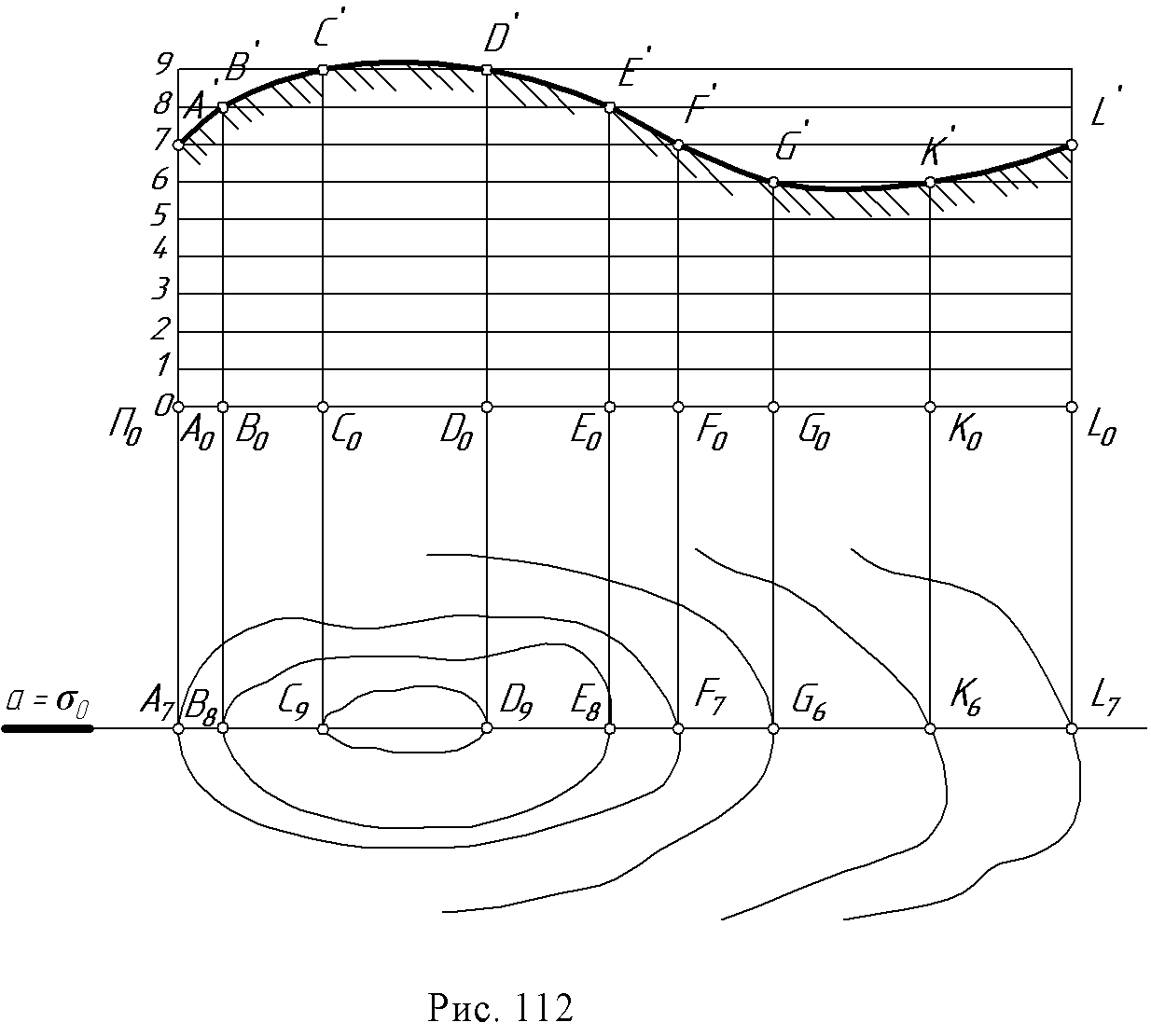
В пересечении одноименных горизонталей находим точки С, D, Е, F, G, K, принадлежащие линиям пересечения откосов со склоном местности. 3. Горизонтали откосов аппарели - прямые линии, но не параллельные бровке дороги. В этом случае горизонтали плоскости каждого откоса строятся как касательные к поверхности прямого кругового конуса. 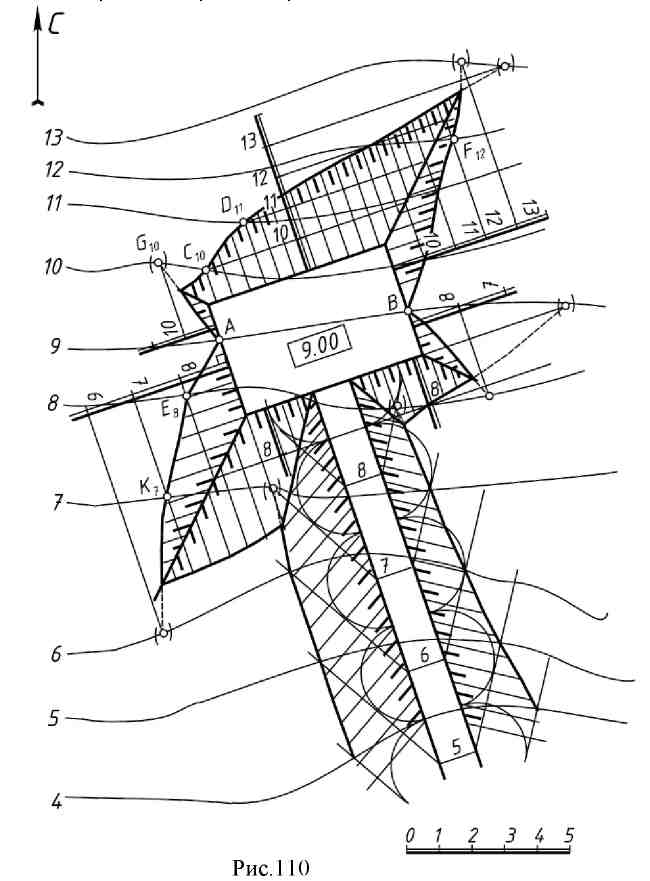 Например, горизонталь 8 откоса аппарели проводится из конца горизонтали 8 самой аппарели (на ее границе) касательно к окружности, проведенной из точки уровня 9. Остальные горизонтали этого откоса параллельны ей, а масштаб уклона откоса перпендикулярен горизонтали 8 как касательная к горизонтали 8 конуса, с вершиной в отметке 9. Пример 2 (рис.111) Построить линии пересечения откосов дорожного полотна с топографической (земной) поверхностью. 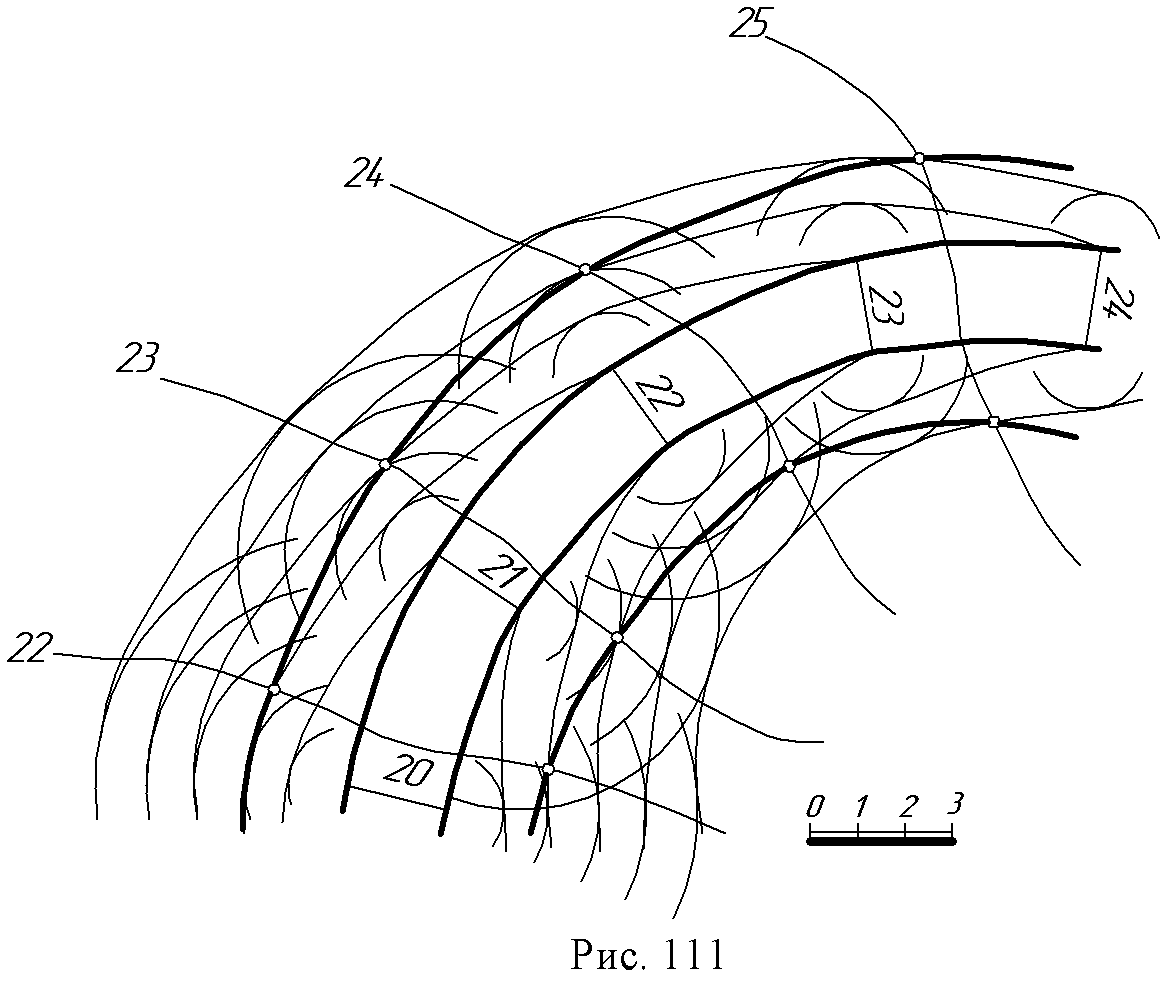 Поверхность откоса является поверхностью одинакового ската. Горизонтали откосов являются огибающими кривыми, проведенными касательно к горизонталям конусов, имеющих одинаковые отметки, аналогично рисунку 107а. Далее находим и соединяем точки их пересечения с равноуровенными горизонталями земли. Пример 3 (рис. 112) Дана топографическая поверхность. Построить ее профиль по линии а. В инженерно – строительном деле профилем называется вертикальное сечение поверхности. Примем прямую а за проекцию σ0плоскости σ, перпендикулярной к нулевой плоскости. Тогда точки А7, В8, С9… L7пересечения σ0с проекциями горизонталей 7, 8, 9, … 7 будут проекциями точек А, В, С, Lпересечения горизонталей поверхности с плоскостью σ. Для построения профиля А', В', …L' совместим плоскость σи ее точки А В… Lснулевой плоскостью.
 15.3. Вопросы для самопроверки
Список литературы
|
