Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
11. Лекция 11. Взаимное пересечение поверхностей. 11.1 Общие положения. При взаимном пересечении поверхностей геометрических тел, следует различать два вида пересечения. К первому виду относятся пересечения, когда все образующие или ребра боковой поверхности одного из тел участвуют в пересечении с поверхностью другого тела. Такой вид пересечения называется полным. Из рис. 78а видно, что все образующие цилиндра G пересекаются с поверхностью цилиндра Ф. 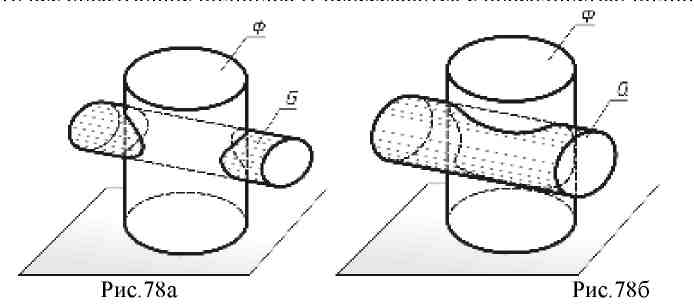 Ко второму виду относятся пересечения, при которых у обоих пересекающихся геометрических тел имеются образующие или ребра боковых поверхностей, не участвующих в пересечении. Такой вид пересечения называется частичным (или неполным) (рис.78б). При полном пересечении образуются две замкнутые линии пересечения (рис. 78а), а при частичном – одна (рис. 78б). Если пересекаются две кривые поверхности, то линия пересечения является замкнутой плавной кривой. При пересечении поверхности гранного тела с кривой поверхностью второго тела линия пересечения представляет собой замкнутую линию, отдельные участки которой являются плавными кривыми, сочлененными друг с другом в точках, расположенных на участвующих в пересечении ребрах гранного тела. В случае пересечения поверхностей двух гранных тел линия пересечения будет представлять собой пространственную замкнутую ломаную линию с точками перелома на ребрах, участвующих в пересечении. Линия пересечения двух поверхностей состоит из ряда точек, принадлежащих одновременно обеим поверхностям (рис. 78в). Нахождение этой линии осуществляется по следующей схеме: 1. Заданные поверхности пересекают вспомогательной плоскостью, называемой посредником - α. Строят линии пересечения посредника с заданными поверхностями: к1 = Ф1 α; к2 = Ф2 α 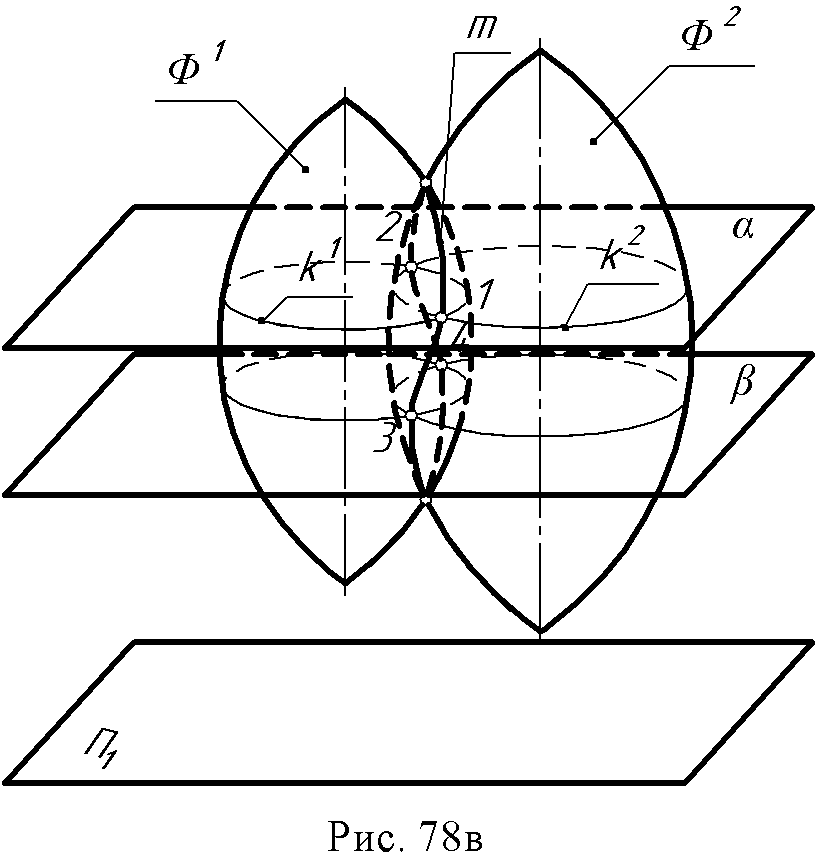 3. Отмечают точки пересечения полученных линий, которые и являются точками линии пересечения заданных поверхностей 1, 2 = к1 к2 Повторив построение с использованием нескольких посредников, определяют ряд точек линии пересечения 3, 4 … Полученные точки соединяют и получают искомую линию пересечения двух поверхностей: m= Ф1 Ф2. Плоскости - посредники выбирают таким образом, чтобы в сечении получались простейшие линии. Это, как правило, для поверхностей вращения - окружности, а для линейчатых поверхностей - образующие. Если с использованием плоскостей - посредников это осуществить невозможно, используют в качестве посредника сферу. В зависимости от вида посредника различают следующие способы построения линий пересечения поверхностей:
Каким бы способом не производилось построение, при нахождении точек линии пересечения двух поверхностей необходимо соблюдать определенную последовательность. Линия будет складываться из опорных и случайных точек. Начинают построения с нахождения опорных точек. Линия пересечения должна находиться в пределах области наложения проекций поверхности. 11.2. Взаимное пересечение многогранников. Линия пересечения многогранников представляет собой одну или две замкнутые ломаные линии. Отрезки ломаной линии являются линиями пересечения граней, а точки излома - точками пересечения ребер одного многогранника с гранями другого и ребер второго с гранями первого. Отсюда два способа решения задачи:
В основе первого способа лежит задача на нахождение точек пересечения прямой (ребра) с плоскостью (гранью) или многогранником; в основе второго способа - построение линии пересечения граней. Второй способ приводит к большому числу графических операций. Найденные точки последовательно соединяют в пределах каждой грани поверхности с учетом видимости. Пример: построить линию пересечения пирамиды SABC с прямой призмой (рис. 79а,б). 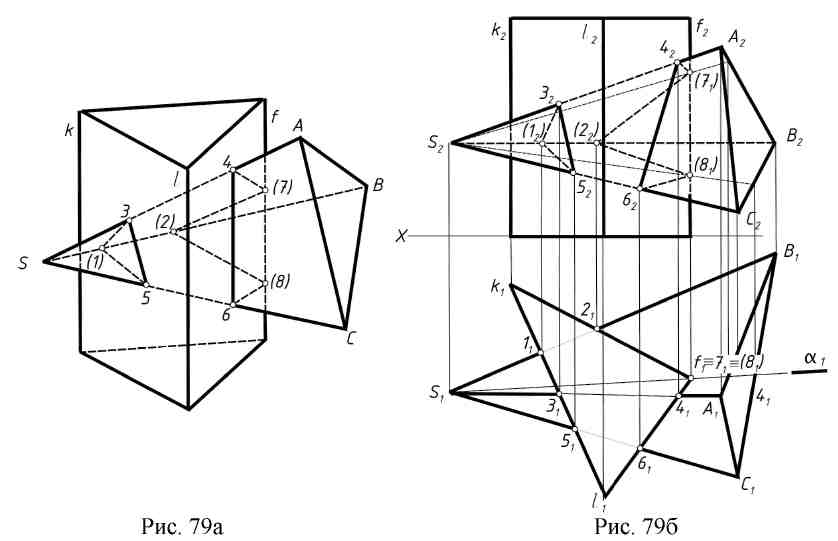 Боковые ребра призмы проецируются в точки, а боковые ее грани являются горизонтально проецирующими отсеками плоскостей. Поэтому эта задача представляет частный случай пересечения, когда одна проекция линии пересечения многогранников известна. Точки пересечения ребер пирамиды с призмой легко определяются на горизонтальной проекции. Отмечают точки 1, 2 как точки пересечения ребра SA соответственно с гранью kl и kf ; точки 3, 4 - пересечения ребра SA с гранями kl и lf; 5, 6 - пересечения ребра SC с гранями kl и lf . Ребра к и l призмы с пирамидой не пересекаются, а для нахождения точек ребра f призмы с пирамидой через него проводим горизонтально - проецирующую плоскость аи, таким образом, получаем точки 7 и 8 соответственно в гранях SAB и SBC. Соединять следует только точки, лежащие в одной грани, например, точки 3 и 5, пересечение грани kl и SAC; 4 и 7 - граней SAB и lf и т.д. Определяем видимость точек на каждой проекции. Условная развертка поверхностей. Для соединения точек можно использовать сетку, в которой каждая линия является ребром поверхности, а промежутки между ними - гранями. Например, точка 1 лежит на ребре SB в грани kl, заносим ее в сетку на линию SB между линиями к и l и т.д. Соединяем точки, в пределах одной клеточки (4-7-2-8-6-4) и (3-1-5-3). Линия пересечения распалась на две части (рис.80). 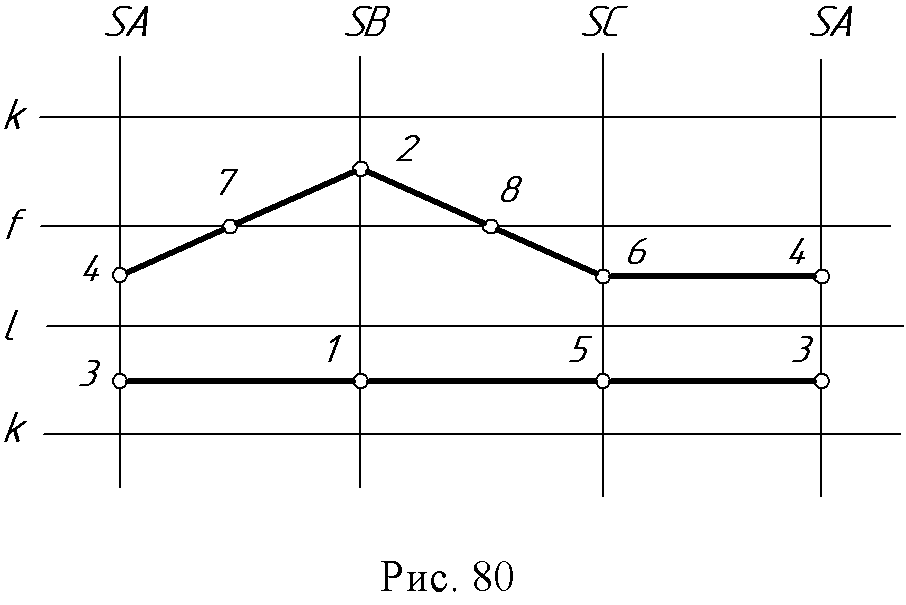 11.3. Пересечение многогранной поверхности с криволинейной. В результате пересечения гранной поверхности с криволинейной получается ломаная линия, состоящая из плоских кривых линий (по числу граней, пересекающих кривую поверхность), сходящихся в точках пересечения ребер с кривой поверхностью. В построениях обязательно нужно определить характерные точки – вершины кривых; точки, которые отделяют видимую часть линии пересечения от невидимой; точки излома, высшую и низшую. Пример: определить линию пересечения конуса и призмы (рис. 81). Горизонтальная проекция линии пересечения совпадает с горизонтальной проекцией призмы, т.к. ее грани - суть горизонтально проецирующие плоскости (рис. 81). Точки пересечения ребер а, в и с призмы с основанием конуса - точки 1, 2 и 3. Высшие точки пересечения каждой грани призмы с конусом являются самыми близкими к оси вращения конуса, и, следовательно, лежат в плоскости β4 ,β5, β6, проходящих через ось конуса, перпендикулярно граням призмы и к П1. Эти точки 4, 5 и 6 лежат одновременно на соответствующих образующих l4, l5, l6 конуса при пересечении его с плоскостями β4 ,β5, β6. Промежуточные точки 7, 8, 9 и 10 найдены при помощи плоскости - посредника а (перпендикулярно оси конуса и параллельно плоскости П1). Промежуточные точки 11, 12, 13, 14, 15, 16 найдены при помощи плоскости - посредника γ (перпендикулярно оси конуса и параллельно плоскости П1). Точка 17 - граница видимости линии пересечения грани bc лежит на правой очерковой образующей конуса. Все полученные точки соединены в пределах каждой грани призмы плавными кривыми с учетом видимости. 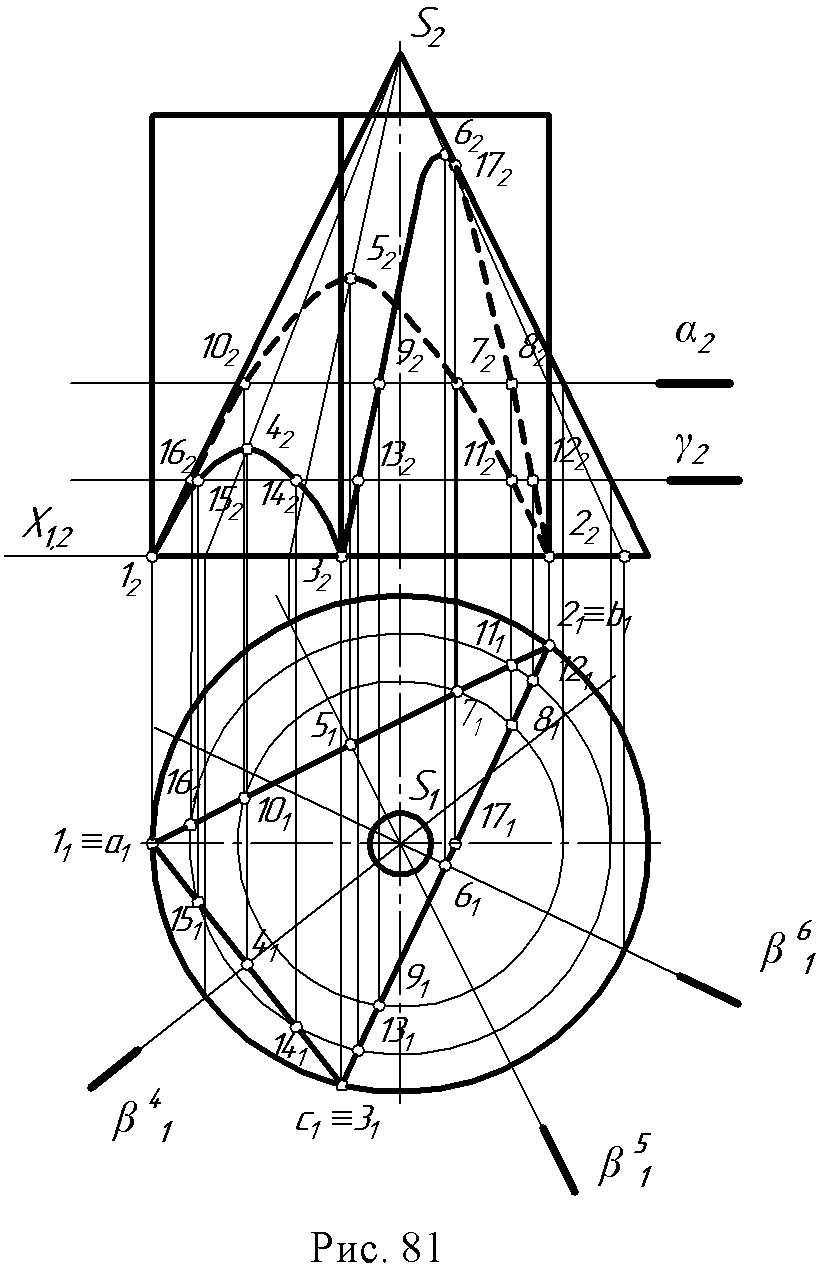 11.4. Вопросы для самопроверки.
12. Лекция 12. Пересечение кривых поверхностей. 12.1. Пример пересечения конуса со сферой. При пересечении двух кривых поверхностей получается пространственная кривая, которая в частных случаях может распадаться на несколько частей. Точки этой линии строятся с использованием основного алгоритма. Пример: определить линию пересечения конуса с частью сферы (рис. 82). 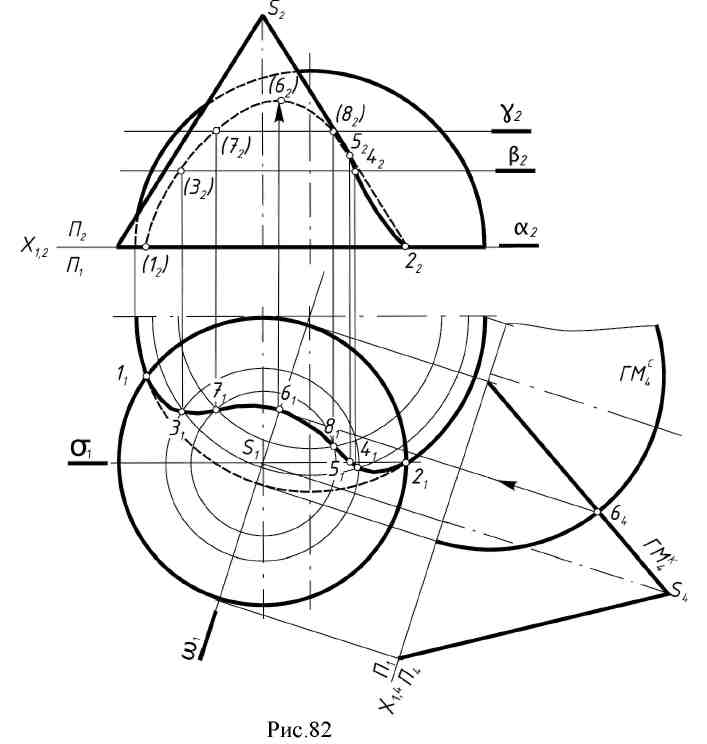 При построении воспользуемся горизонтальными плоскостями - посредниками (а, β, γ) т.к. именно эти плоскости дают в сечении с заданными поверхностями простейшие линии (параллели). От пересечения заданных поверхностей плоскостью а основания конуса и экватора сферы получаем точки 1 и 2, плоскости β- точки 3 и 4, плоскости γ-точки 7 и 8. Точка 5 - точка видимости линии сечения находится при помощи плоскости σ (σ // П2; σS). Для нахождения высшей точки линии сечения проводим через оси заданных поверхностей плоскость ω1, перпендикулярную горизонтальной плоскости проекций. Для упрощения построения заменим плоскость П2на П4, для плоскости П4плоскость ω является плоскостью главных меридианов обеих поверхностей, и следовательно, точка пересечения очерковых линий поверхностей на плоскости П4является высшей точкой (точка 6). Полученные точки соединяют плавной кривой, которая идет через точки 1-3-7-6-8-5-4-2. 12.2. Частные случаи пересечения поверхностей вращения второго порядка. При пересечении поверхностей второго порядка линией пересечения в общем случае является пространственная кривая четвертого порядка. Эта кривая пересекается с плоскостью в четырех точках (действительных и мнимых). Порядок линии пересечения равен произведению порядков пересекающихся поверхностей. Кривая четвёртого порядка может распадаться на две плоские кривые второго порядка. Теорема 1. Если две поверхности пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются (доказательство не приводится). 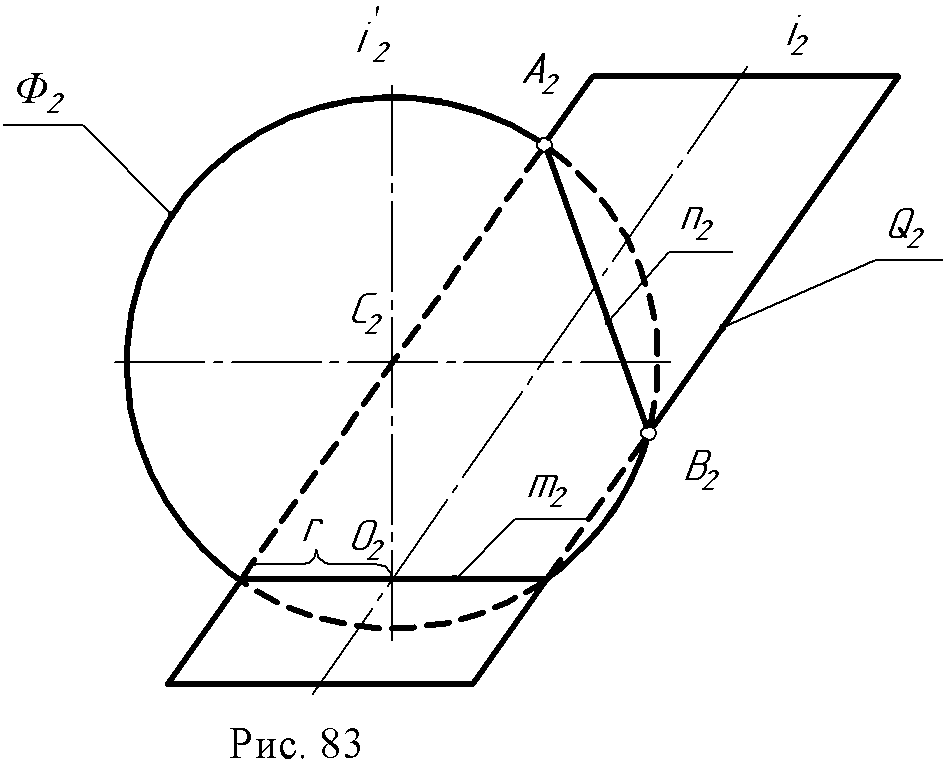 На рис. 83 изображены фронтальные проекции Ф2и Q2сферы Ф и эллиптического цилиндра Q, имеющих общую окружность m с центром (О2). Для данных поверхностей, плоскость, определяемая точкой С и осью I, является плоскостью симметрии (С,i || П2). Общая окружность радиуса r - одна из плоских кривых линии пересечения. Вторая линия пересечения спроецируется на плоскость П2в виде отрезка прямой n2. Для его построения следует воспользоваться точками А2и В2, принадлежащими фронтальным очеркам заданных поверхностей. Теорема 2 (о двойном касании). Если две поверхности имеют касание в двух точках А и В, то линия пересечения распадается на две плоские кривые второго порядка, плоскости которых проходят через отрезок АВ, соединяющий точки касания. Пример: по двум окружностям m и n пересекается сфера Ф с поверхностью эллиптического цилиндра Q (рис. 84). 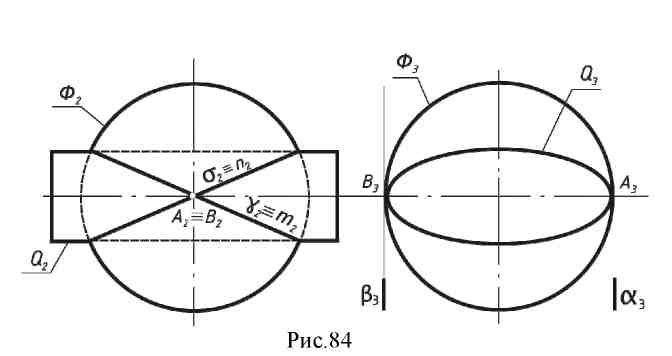 Точки касания и касательные плоскости обозначены соответственно через А, В, аА, βВ. Окружности, на которые распалась линия пересечения поверхностей, расположены во фронтальных проецирующих плоскостях γи σ(γ m, σ n). Теорема 3 (Теорема Г. Монжа). Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую соединяющую точки пересечения линий касания (рис. 85). 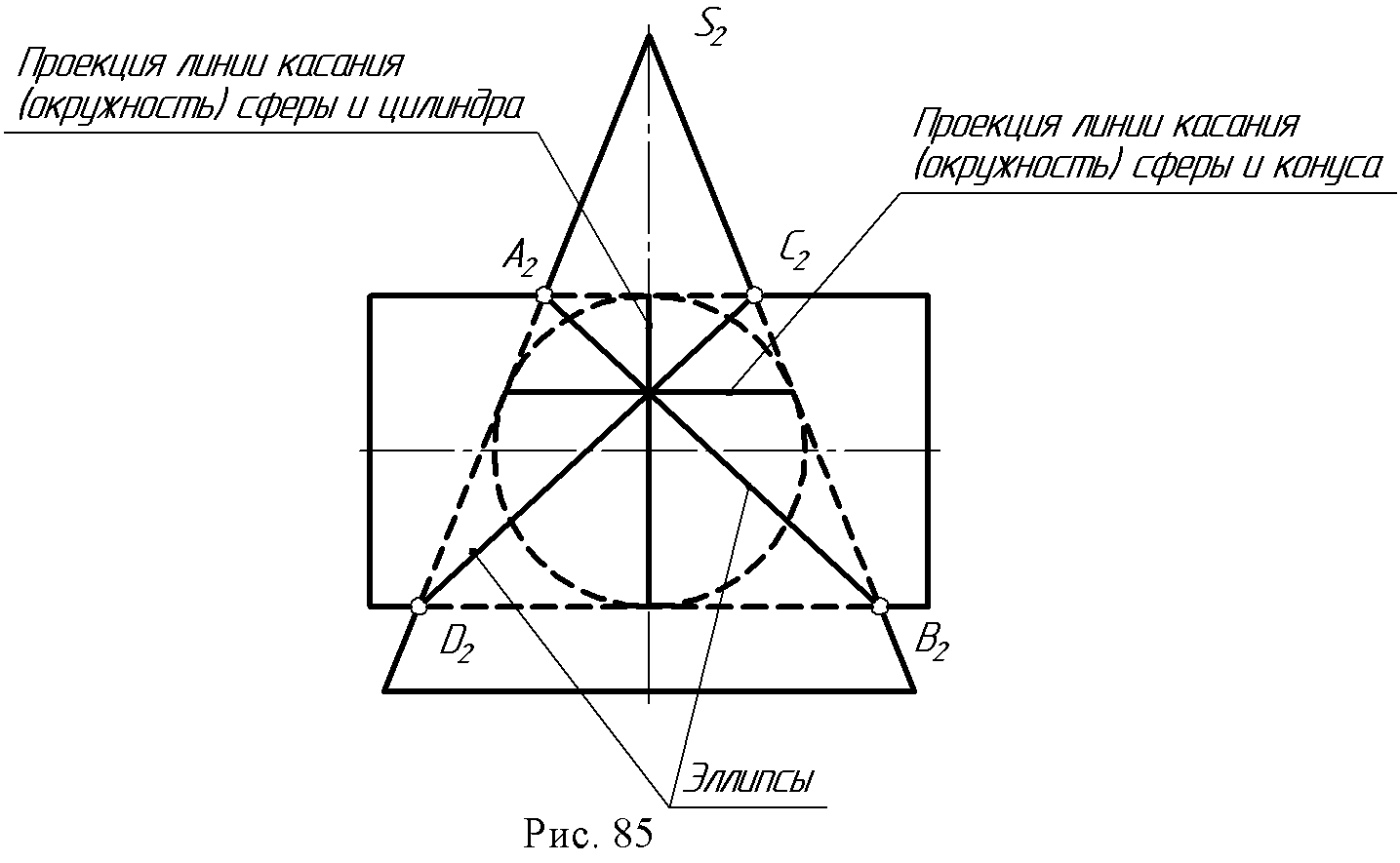 12.3. Метод концентрических сфер. Для построения линии пересечения двух поверхностей вращения, оси которых пересекаются, иногда нецелесообразно использовать вспомогательные секущие плоскости, т.к. они могут не дать вспомогательных линий сечения, которые проецировались бы графически простыми линиями. Прежде чем приступить к построению линии пересечения поверхностей вращения рассмотрим соосные поверхности. Соосными называются поверхности, имеющие общую ось. Две соосные поверхности пересекаются по окружностям, перпендикулярным общей оси. Пример: соосные сфера и конус вращения пересекаются по линиям т и п. Точки А и В, вращаясь вокруг общей оси I, дадут окружности, принадлежащие конусу и сфере, которые и будут линиями их пересечения. Свойство сферы 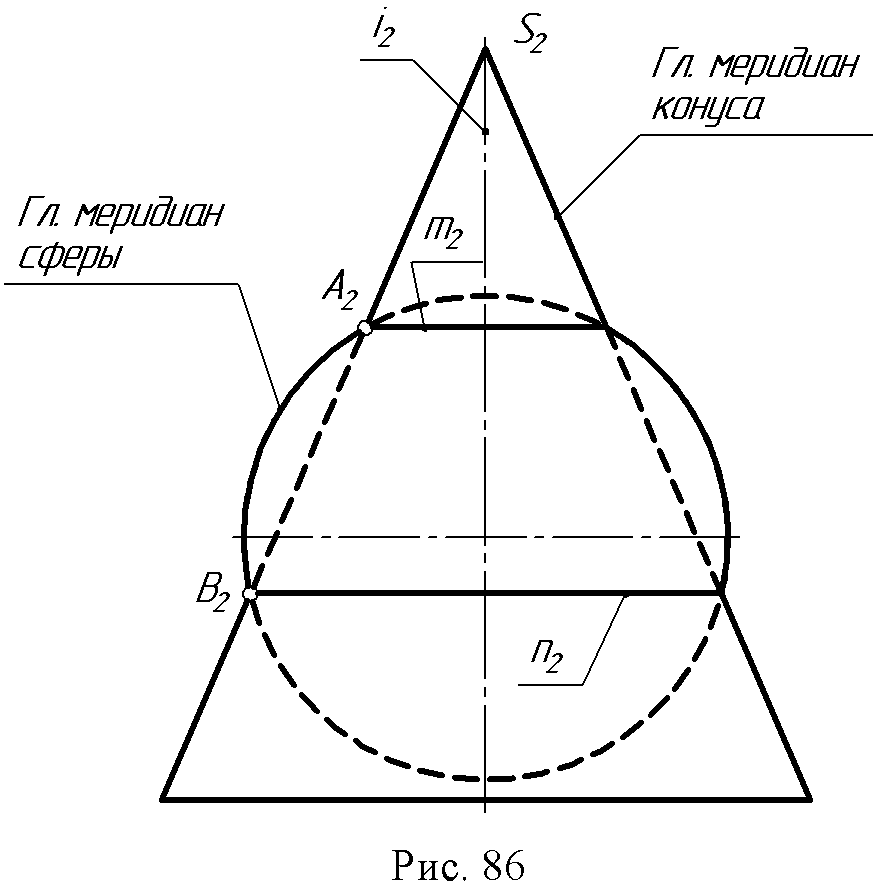 пересекать соосную с ней поверхность вращения по окружностям (параллелям поверхности) положено в основу способа применения сфер как посредников при нахождении линии пересечения поверхностей вращения. Для того чтобы вспомогательная секущая сфера пересекала по параллелям обе заданные поверхности, центр сферы должен лежать в точке пересечения осей заданных поверхностей. Если оси поверхностей вращения параллельны плоскости проекций, то параллели пересечения вспомогательной сферы с этими поверхностями проецируются на эту плоскость в прямые линии. Это - основа метода секущих концентрических сфер. Пример: определить линию пересечения тора и конуса (рис. 87). Заданы поверхности вращения, оси их пересекаются в точке О и по условию лежат в плоскости, параллельной фронтальной плоскости проекций. Из точки О2проведем сферу произвольного радиуса R1,, которая тор пересекает по линиям к2и l2, конус по линиям т2и п2в пересечении которых определены точки А2и В2, которые принадлежат фронтальной проекции линии пересечения тора и конуса. 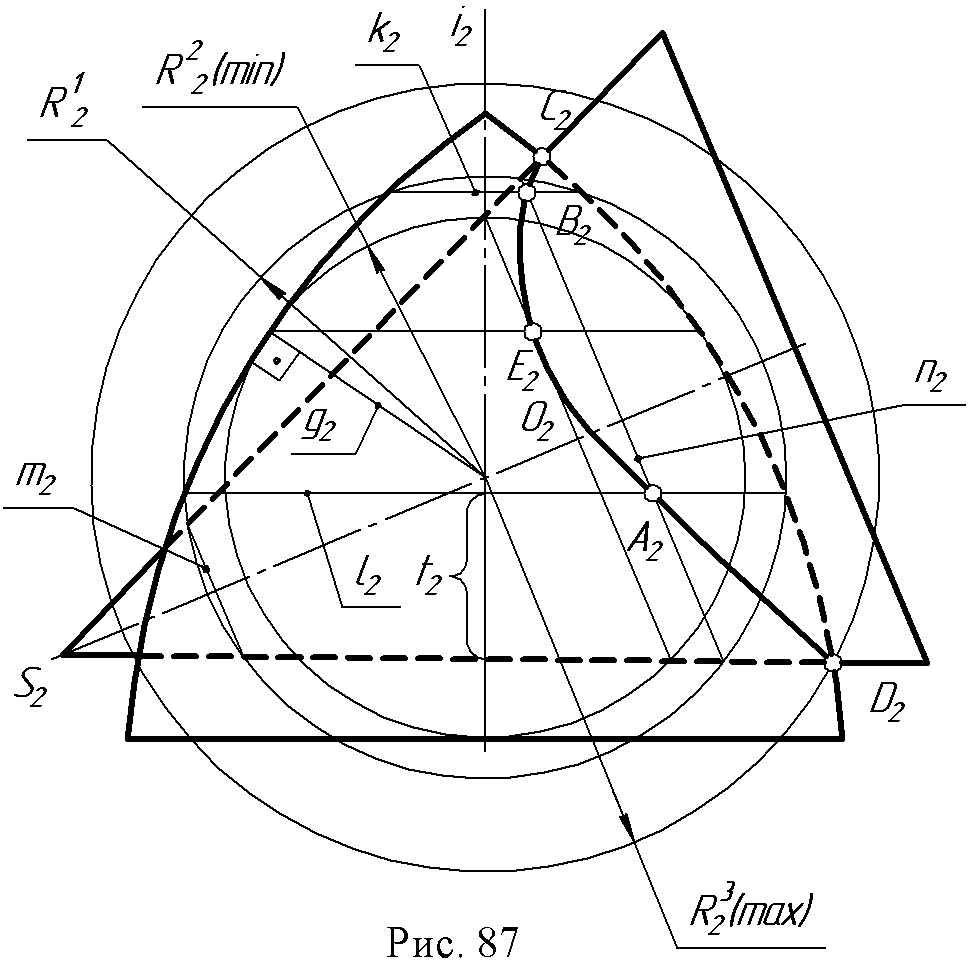 Изменяя радиус вспомогательных сфер, можно получить какое угодно число точек линии пересечения. Для определения максимального радиуса сферы, необходимо отметить точки пересечения очерковых линий, замерить расстояние от точки O2до этих точек и наибольшее из этих расстояний будет максимальным радиусом сферы (R3). Для определения радиуса наименьшей сферы нужно из точки O2провести нормали к очерковым линиям каждой поверхности (g2и t2). Больший из полученных отрезков и будет минимальным радиусом вспомогательной сферы (R2). При помощи этой сферы найдена точка Е2. Именно с нее следует начинать искать точки линии пересечения поверхностей. Найденные точки соединяют плавной линией. Если нужно построить проекции этой линии на другие плоскости проекций, то это легко сделать, связав каждую точку пересечения с окружностью, лежащей на этой или другой поверхности вращения. 12.4. Вопросы для самопроверки.
13. Лекция 13. Развертки поверхностей. 13.1. Общие положения. В инженерной практике развертывание поверхностей находит применение при разработке чертежей для раскроя плоского листового материала. Способы развертки поверхностей используются при проектировании тентовых сооружений, при строительстве резервуаров различной формы, воздуховодов и т.д. Обычно поверхность рассматривают как гибкую нерастяжимую оболочку. Развертыванием поверхности называется такое преобразование ее, в результате которого поверхность совмещается с плоскостью без складок и разрывов, а плоская фигура, полученная в результате этого преобразования, называется разверткой. В противном случае поверхность называется неразвертывающейся, и тогда для построения развертки ее разбивают на части, которые можно приближенно заменить развертывающимися поверхностями, а затем строить развертки этих частей. |
