Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
13.2. Развертывающиеся поверхности и их свойства. Поверхность Q называется развертывающейся (рис. 88) на плоскость Q , если поверхность и ее развертку можно рассматривать как точечные множества, между которыми устанавливается взаимно однозначное соответствие. Это соответствие обладает рядом важных свойств. Свойство 1. Каждой точке поверхности соответствует единственная точка на ее развертке М0 – M0. Свойство 2. Каждой кривой линии на поверхности в общем случае соответствует кривая на ее развертке, длина кривой линии равна длине ее преобразова- ния S (AB )→ S(A B). Свойство 3. Угол между кривыми линиями (угол между касательными к кривым в точке их пересечения) на поверхности равен углу между преобразова- ниями этих кривых линий на развертке φ = φ. Свойство 4. Замкнутая линия на поверхности и соответствующая ей линия на развертке ограничивают одинаковую площадь: площадь F = площадь F. Если какой - нибудь дуге CD, расположенной на поверхности, соответствует на раз- вертке отрезок прямой C D, то дуга CD будет кратчайшей на поверхности и будет называться геодезической линией. 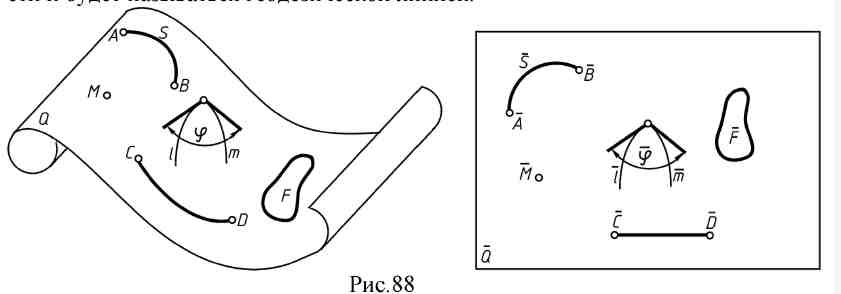 В курсе дифференциальной геометрии доказывается, что линейчатая поверхность – развертывающаяся, если касательная плоскость, проведенная в какой – нибудь точке поверхности, касается ее во всех точках прямолинейной образующей, проходящей через эту точку. Значит, у развертывающейся линейчатой поверхности касательная плоскость во всех точках одной образующей постоянна. К числу развертывающихся поверхностей относятся многогранные поверхности; из линейчатых – цилиндрические, конические, торсовые. Для многогранных поверхностей строят точные развертки, построение которых сводится к определению натуральных величин граней и затем построению их последовательно на чертеже. Для линейчатых поверхностей строят приближенные развертки, при этом заданную поверхность заменяют (аппроксимируют) другой, которая или вписана в данную поверхность, или описана около нее, и которая развертывается. 13.3. Основные графические способы построения разверток поверхностей. 1. Способ треугольников (триангуляции). Этот способ применяют для построения разверток гранных и всех развертывающихся линейчатых поверхностей. Способ триангуляции для этих поверхностей универсален. Сущность способа заключается в том, что кривую линейчатую поверхность заменяют вписанной в нее многогранной с треугольными гранями, нахождению натурального вида их и последовательному построению на чертеже. Пример: Построить развертку эллиптического конуса, заданного круговым основанием с вершиной S (рис. 89а,б). Впишем в заданный конус двенадцатигранную пирамиду, имеющую в основании правильный 12-угольник. Далее заменим дуги основания хордами и определим ошибку этой замены. Она составит: . Поверхность имеет плоскость симметрии, которая проходит через ось конуса параллельно фронтальной плоскости проекций. Поэтому можно построить развертку для половины поверхности. Способом прямоугольного треугольника определяем натуральные величины сторон треугольников S1, S2 … Так как превышение точки S над точками 1, 2, 3 и т.д. постоянная величина ZS, то прямоугольный треугольник строим на фронтальной проекции. Один катет ∆Z=ZS, а второй - длина горизонтальной проекции отрезков (S111, S121 … и т.д.). Гипотенузы прямоугольных треугольников дают натуральные величины отрезков S1, S2 и т.д. Натуральные величины отрезков А1, 12, 23 и т.д. можно замерить на горизонтальной проекции, т.к. они параллельны этой плоскости, т.е. А1 = А111; 12=1121 и т.д. Затем каждый треугольник графически строят по трем сторонам, один примыкает к другому. На произвольной линии откладываем отрезок А0S0= /AS / = A2S2 и на нем достраиваем треугольник со сторонами S1 и А1 (из точки S0проводят дугу радиуса S1, а из точки А0 - дугу радиуса А1, в пересечении этих дуг получена точка 10).  Все последующие треугольники строятся аналогично, после чего через точки развернутого по способу хорд основания конуса проводят по лекалу плавную линию. Надо обратить внимание на одну из опорных точек развертки окружности основания конуса точку 40. Она является точкой перегиба и получается из той точки основания, через которую проходит образующая поверхности, являющаяся линией границы видимого контура по отношению к плоскости основания конуса (рис. 89б). Фактически на рис. 89 построена развертка пирамидальной поверхности. Пример 2. Построить развертку поверхности цилиндроида (рис. 90а,б). Заменяется данная поверхность вписанной в нее многогранной поверхностью, так же состоящей из треугольников: строятся натуральные величины этих треугольников так же, как это было сделано в примере 1, и, проведя через их вершины по лекалу плавные кривые, получаем приближенную развертку поверхности цилиндроида (рис. 90б). 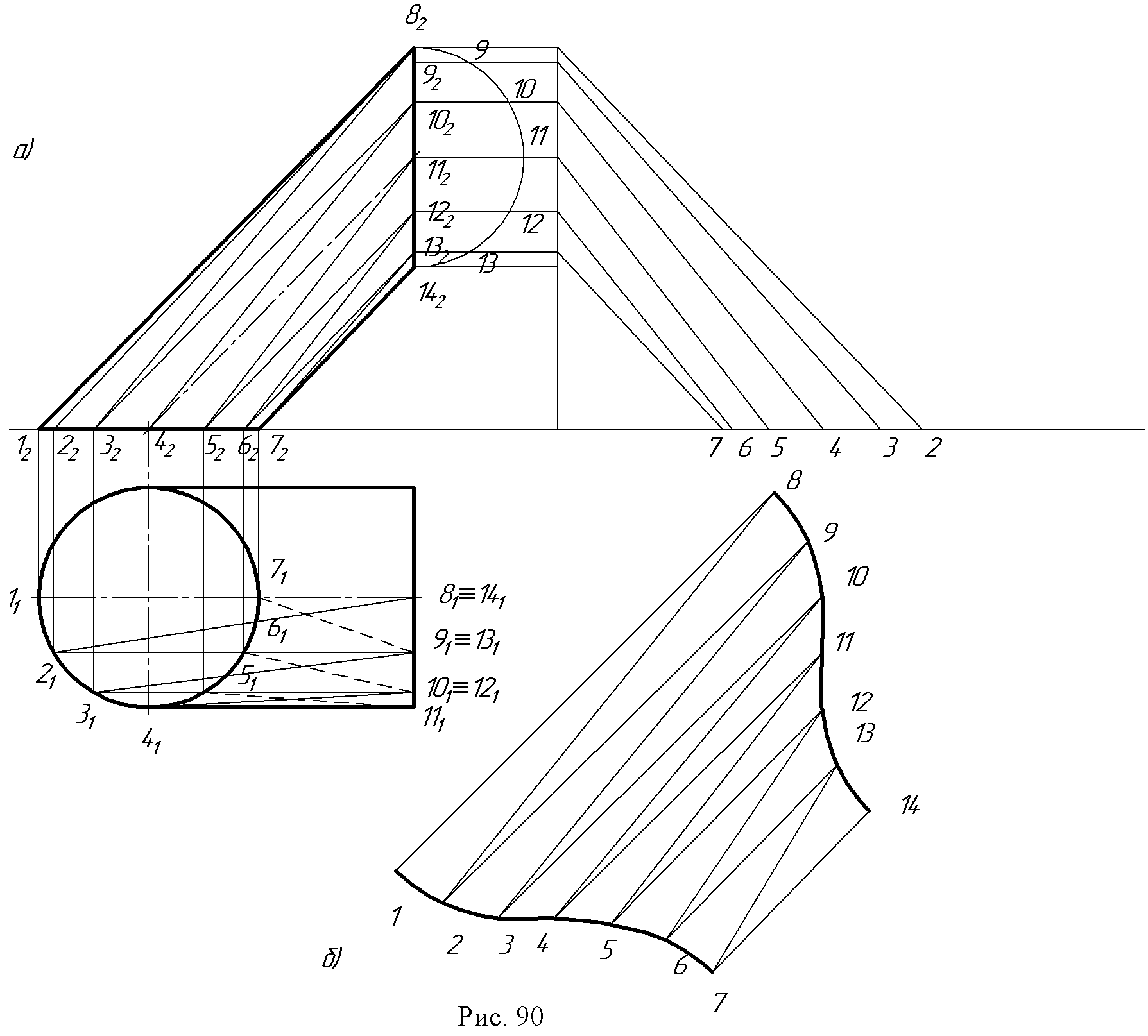 Для развертывания боковой поверхности прямого кругового конуса (рис. 91) используется известное из стереометрии построение с подсчетом угла сектора, представляющего собою искомую развертку φ0 = R/Lx 360º , где R - это радиус основания конуса, L - длина его образующей. Способ нормального сечения (рис. 92) используется для построения развертки призматических и цилиндрических поверхностей. Построение разверток указанных поверхностей приводит, в общем случае, к многократному построению натурального вида трапеций и параллелограммов, из которых состоит данная призматическая поверхность или призматическая поверхность, описанная или вписанная в данную цилиндрическую поверхность и заменяющая её. 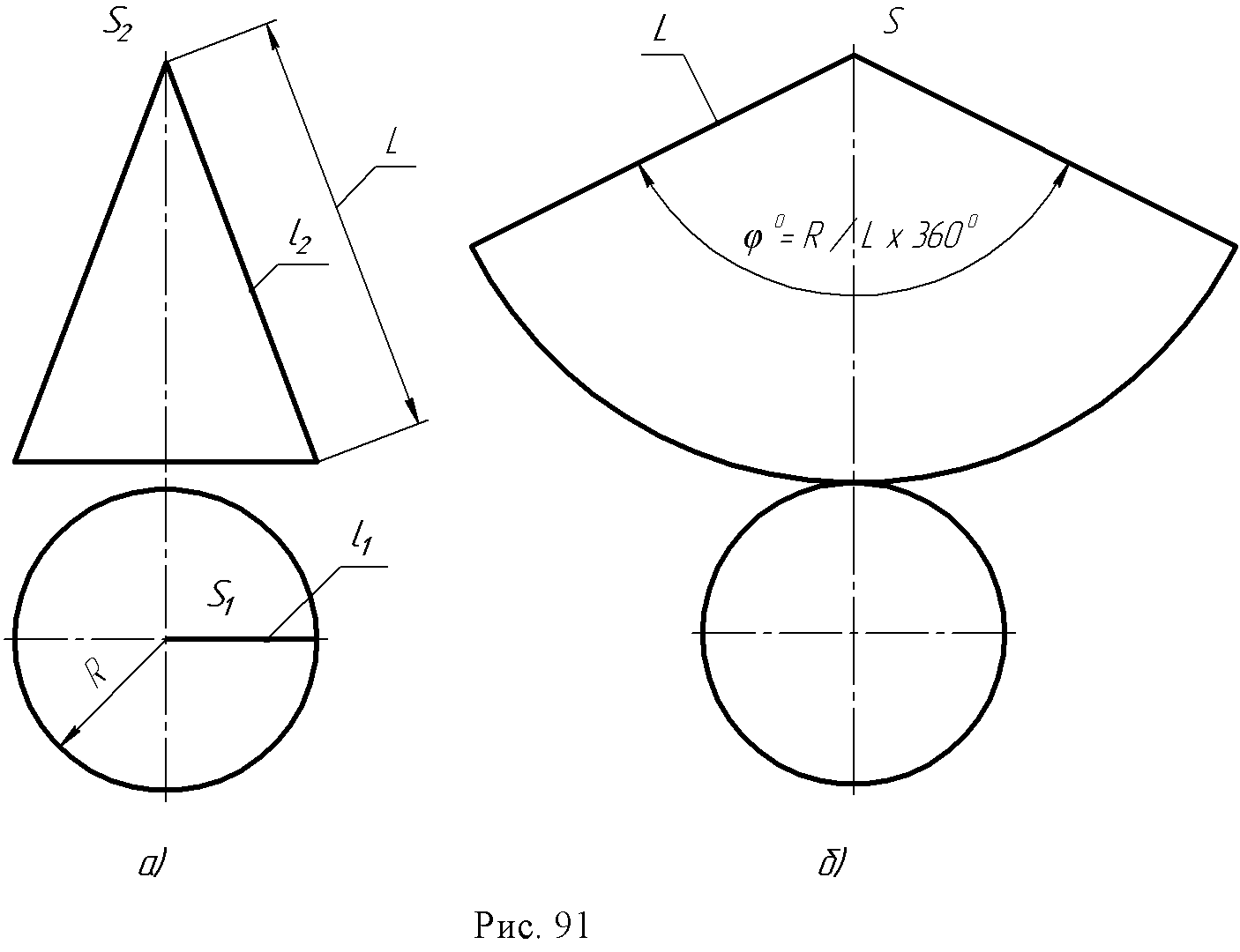 Построение трапеций или параллелограммов производится по их основаниям и высотам, причем необходимо знать отрезки оснований, на которые они делятся высотами (рис. 92). 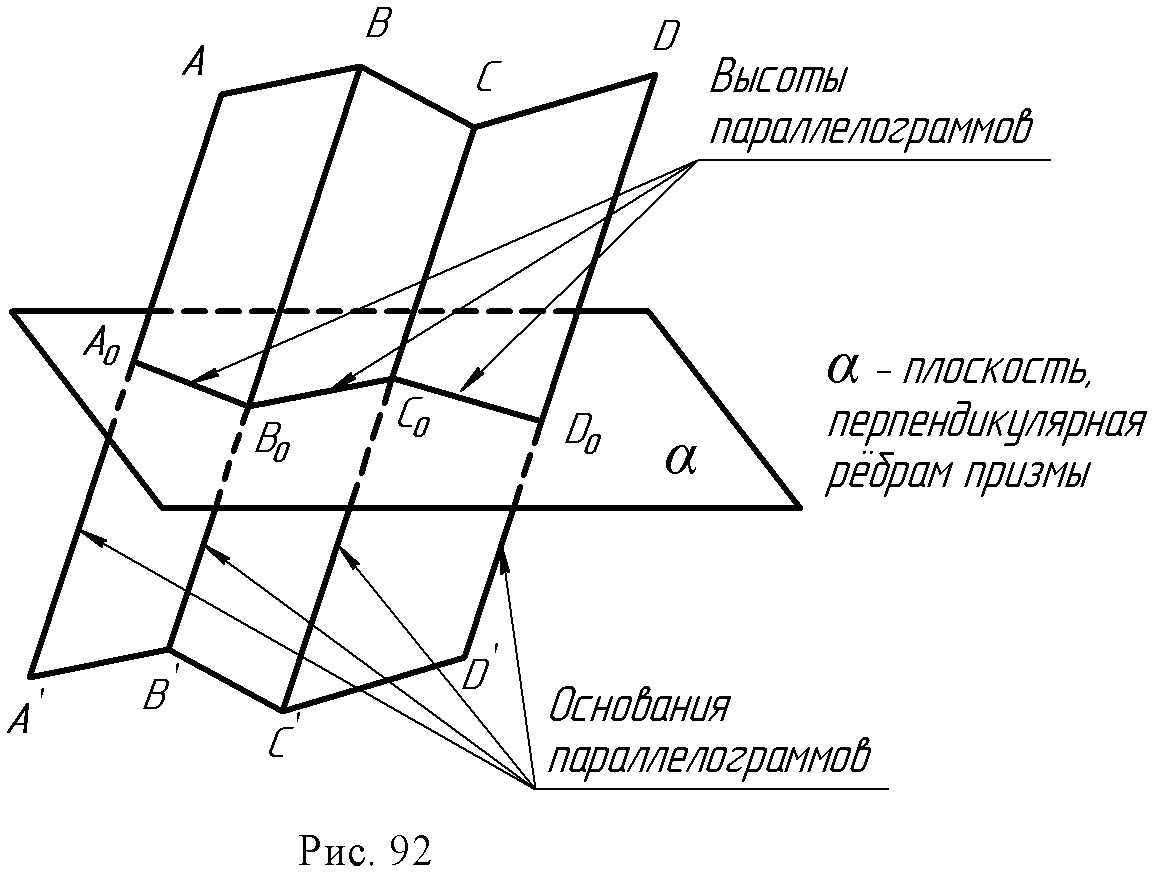 Поэтому для построения развертки необходимо предварительно пересечь поверхность плоскостью, перпендикулярной к ребрам. Стороны этого сечения и будут высотами трапеций или параллелограммов, из которых состоит поверхность. Пример: Построить развертку поверхности эллиптического цилиндра (рис. 93а). 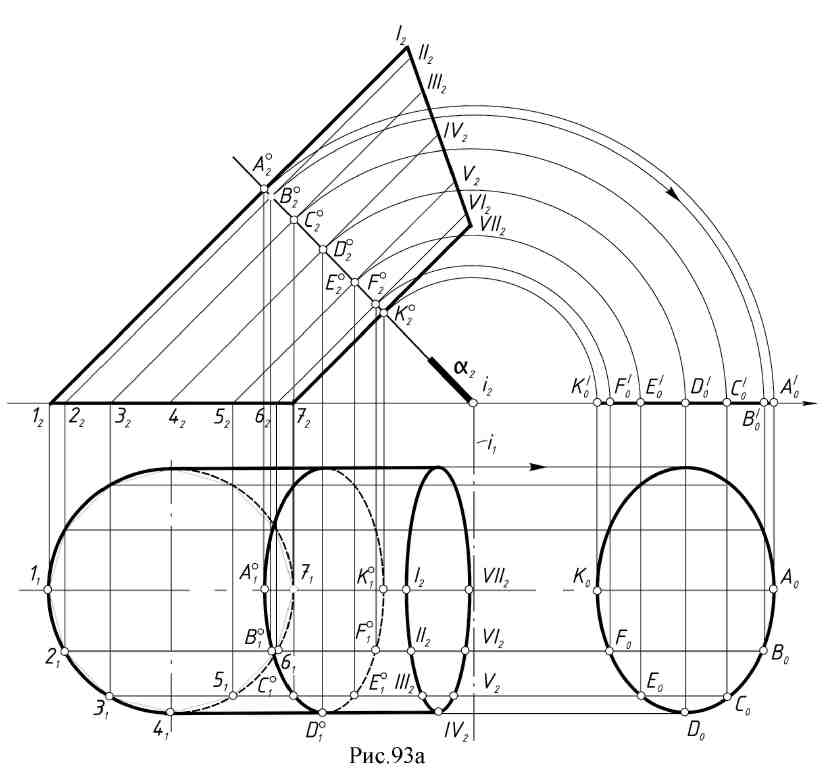 В заданную поверхность вписана 12-угольная призма, для чего основание цилиндра разделено на 12 равных частей и проведены ребра параллельно образующим цилиндра. Проводим плоскость нормального сечения а(а2) перпендикулярно фронтальным проекциям образующих и строим проекции (А1, В1, С1, D1 … и А2, В2, С2) и натуральную величину нормального сечения А0, В0, С0, D0 … (способом вращения вокруг проецирующей оси i). На произвольной горизонтальной линии откладываем отрезки А0В0, В0С0, С0D0, D0Е0 … и т.д. Через полученные точки А0,, В0, С0и т.д. проводим перпендикуляры, на которых откладываем длины ребер (образующих, взятые с фронтальной проекции, так как они являются фронталями (рис. 93б). Точки I0, II0, III0и т.д. - развертка окружности верхнего основания; 10, 20, 30 и т.д. - развертка окружности нижнего основания цилиндра. Полученная фигура является разверткой боковой поверхности цилиндра. Построение разверток призматических поверхностей производится аналогично. 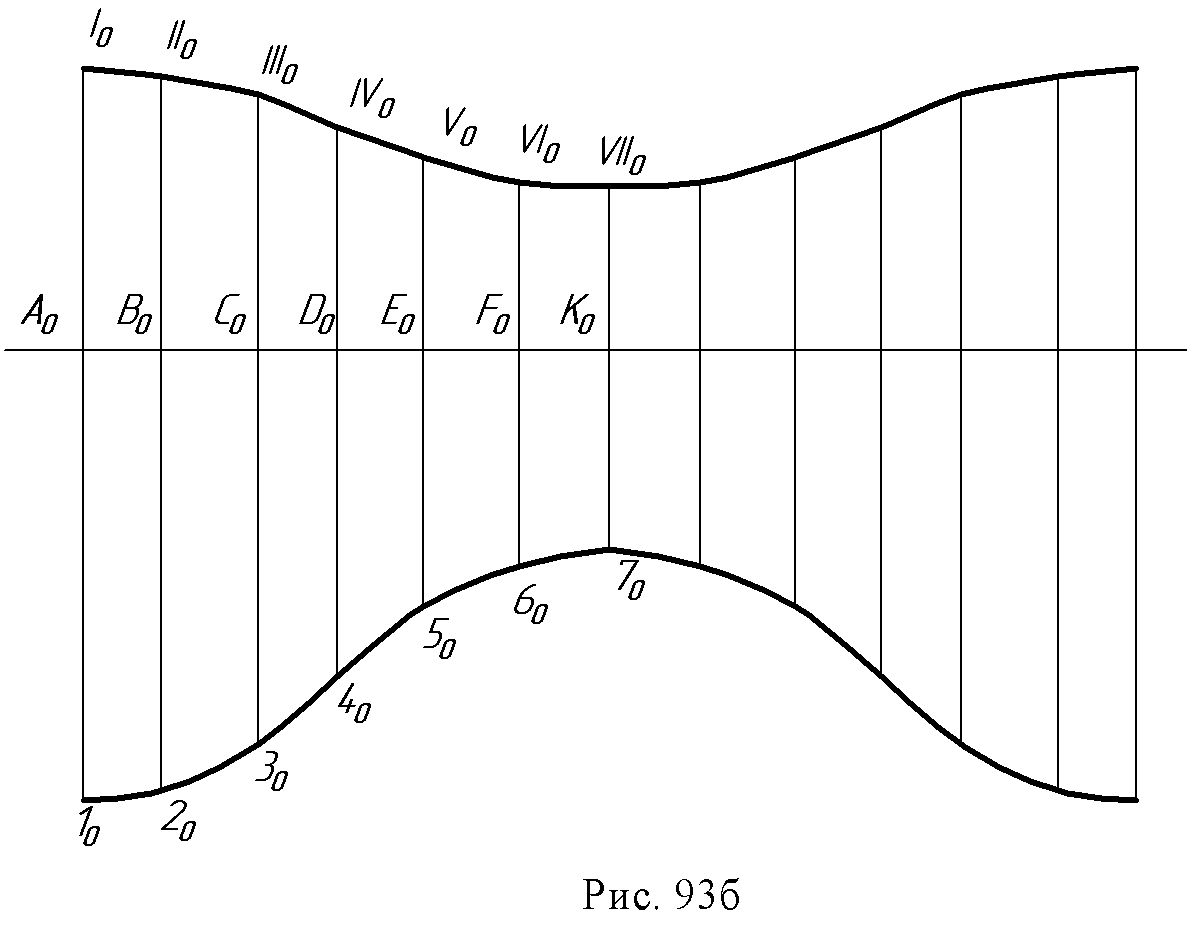 13.4. Построение условных разверток неразвертывающихся поверхностей вращения. Способ построения этих разверток состоит в том, что данная поверхность вращения разбивается с помощью меридианов на сравнительно узкие, равные между собой доли. Каждая такая доля заменяется описанной цилиндрической поверхностью, которая касается данной поверхности в точках среднего меридиана земли. Этот средний меридиан является нормальным сечением цилиндрической поверхности. Границами цилиндрической поверхности будут плоскости меридианов (α1 и β1) ограничивающих рассматриваемую долю. Например, так будет выглядеть развертка долей сферической поверхности (рис. 94). 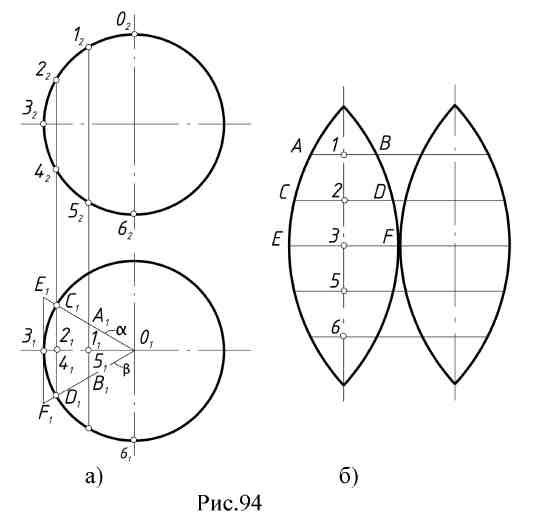 13.4. Вопросы для самопроверки.
4. Укажите последовательность графических построений разверток поверхностей конуса и цилиндра.
14. Лекция 14. Проекции с числовыми отметками 14.1. Сущность метода. Проекции точки. В инженерной практике существуют такие объекты, для которых метод двух изображений непригоден: размеры длины и ширины значительно больше вертикальных размеров, изображения получаются мало наглядными, а точность графических построений на таких чертежах недостаточна для решения позиционных и метрических задач. В строительном деле такими объектами являются участки земной поверхности с различными сооружениями на ней: дорогами, плотинами ГЭС, аэродромами, каналами, строительными площадками и т.п. Высота указанных сооружений обычно весьма мала по сравнению с длиной и шириной. Для изображения рельефа земной поверхности и проектирования на ней инженерных сооружений практика создала более удобный и простой метод – метод проекций с числовыми отметками. Сущность метода проекций с числовыми отметками заключается в том, что данный предмет ортогонально проецируется только на одну горизонтальную плоскость. П0 – плоскость нулевого уровня. При этом для получения изображения, однозначно соответствующего данному предмету, около проекций отдельных точек пишут (справа) числа, указывающие расстояние (обычно в метрах) от данных точек до плоскости П0. Эти числа и называют числовыми отметками. Перед числовыми отметками ставят знак минус, если точка расположена ниже плоскости нулевого уровня; если точка расположена над плоскостью, то ее отметка считается положительной. Отметка точки, инцидентной нулевой плоскости, называется нулевой (рис. 95). 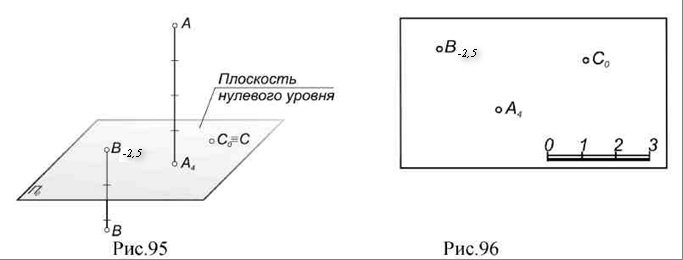 Изображение этих трех точек в проекциях с числовыми отметками дано на рис. 96, где плоскость П0совмещена с плоскостью чертежа. На планах необходимо вычерчивать линейный масштаб, который необходим для чтения чертежа. 14.2. Проекции прямой Прямая общего положения задается проекциями двух принадлежащих ей точек с указанием их отметок. Спроецируем две произвольные точки А и В данной прямой на плоскость П0. Прямая, соединяющая проекции этих точек, будет проекцией данной прямой только тогда, когда проекции точек будут дополнены числовыми отметками, например А5В3. В противном случае эта прямая будет проекцией всех прямых, лежащих в горизонтально – проецирующей плоскости σ, проходящей через данную прямую АВ (рис. 97б). 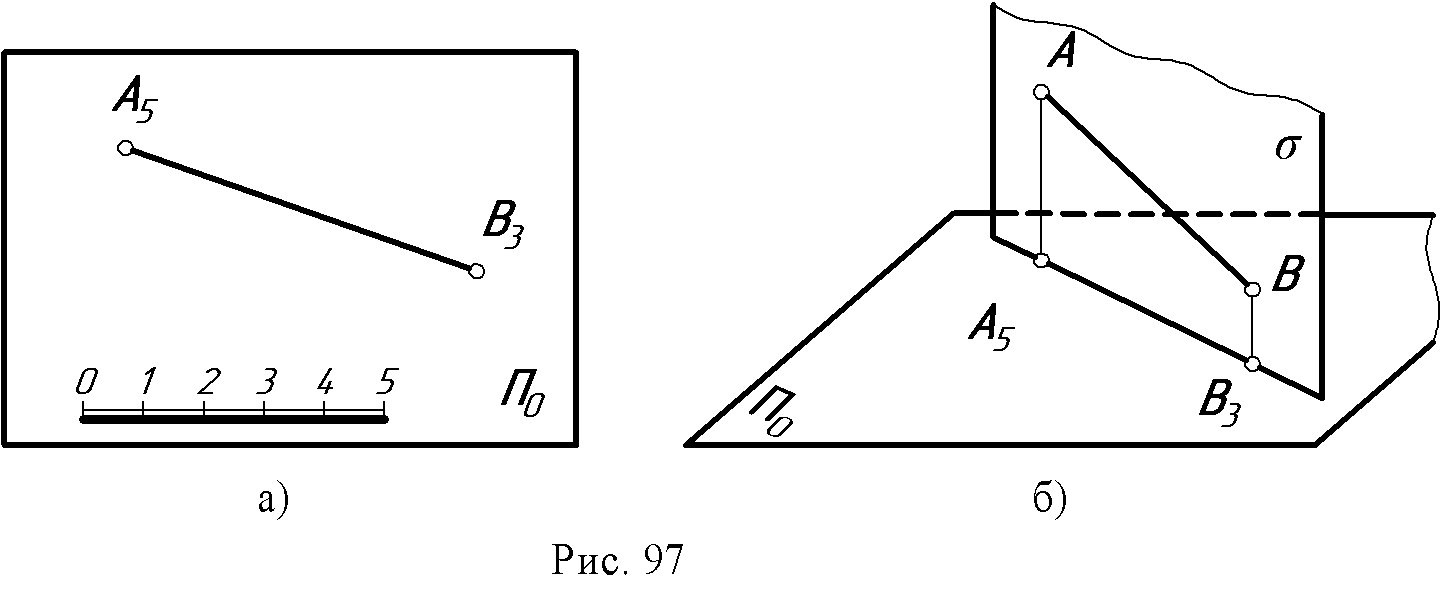 Истинная величина отрезка прямой и угла наклона ее к нулевой плоскости П0. Совмещаем плоскость σ с П0 вращением вокруг проекции А1В4данной прямой АВ (рис. 98). При этом прямая АВ, совместившись с П0, займет положение А1В1. Очевидно, что отрезок А1В1 равен истинной величине АВ, а угол α между проекцией данной прямой и ее совмещенным положением равен истинной величине угла наклона АВ к плоскости П0. 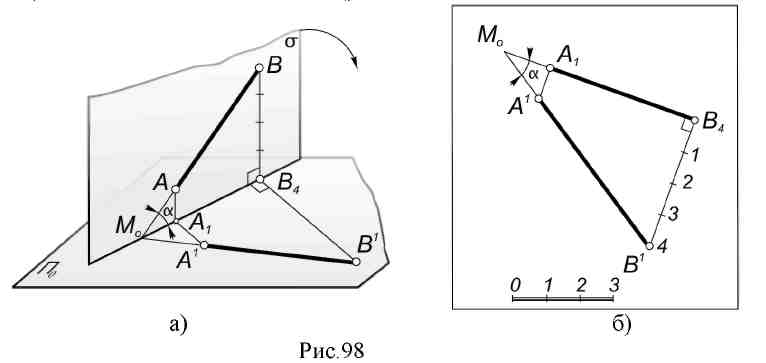 Фигура А1В4 В1А1является трапецией с параллельными сторонами А1А1и В1В4, перпендикулярными А1В4(рис. 98а). Для определения истинной (натуральной) величины отрезка необходимо на плане прибегнуть к построению трапеции (рис. 98б): 1. Через проекции точек, ограничивающих отрезок, провести прямые, перпендикулярные к проекции этого отрезка; 2. В масштабе чертежа отложить на этих перпендикулярах от их основания высоты соответствующих точек; при разных знаках высоты откладываются в разные стороны; 3. Прямая, соединяющая полученные точки, равна истинной величине данного отрезка. Угол между проекцией и прямой равен истинной величине угла наклона прямой к горизонтальной плоскости П0. Следом прямой АВ на нулевой плоскости будет точка М (рис. 98б) - точка пересечения продолжения этой прямой с продолжением ее проекции. Проекция М0 следа совпадает с точкой М и будет иметь ту же отметку, что и основная плоскость. Интервал и уклон прямой. Длина проекции отрезка прямой называется его заложением и обозначается буквой L (рис. 99), разность расстояний концов отрезка до плоскости П0называется превышением и обозначается буквой Н. 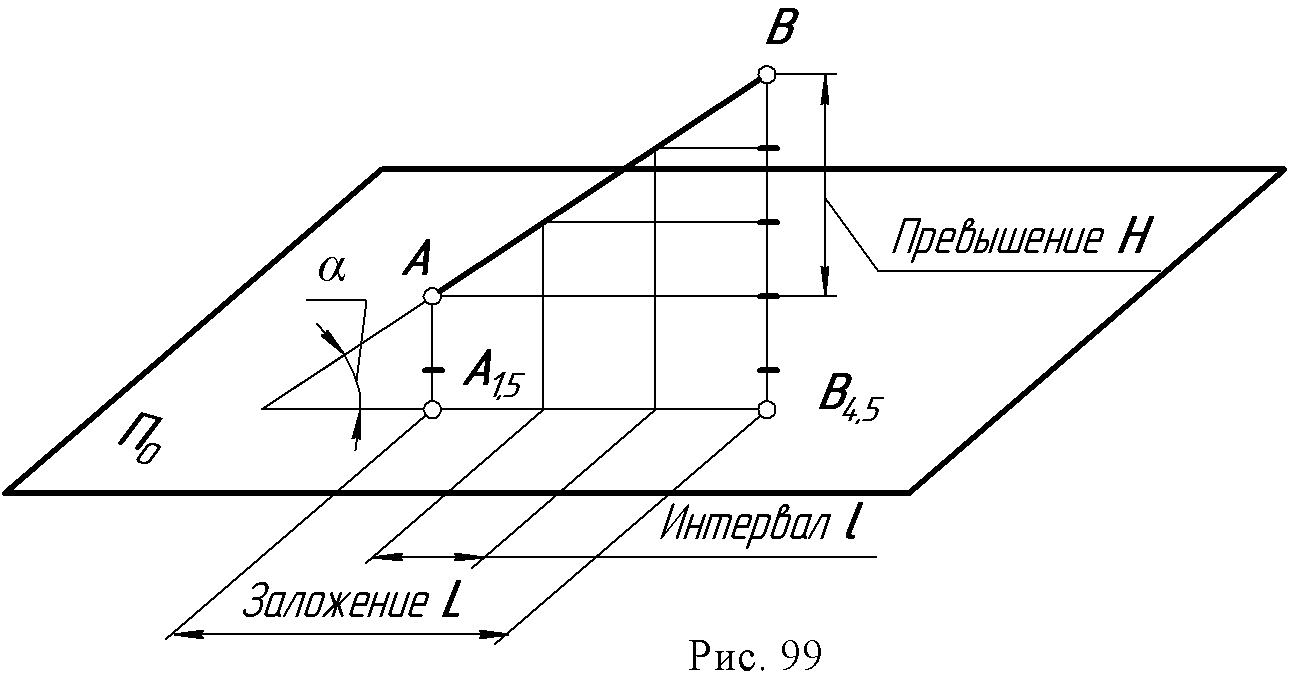 Наклон прямой может быть выражен не только величиной угла α, но также уклоном. Уклон - i - равен тангенсу угла наклона прямой к плоскости П0: i =H / L = tg α. Если превышение равно единице (Н=1), то заложение, ему соответствующее, называется интервалом и обозначается буквой l. Уклон в этом случае равен i=1 / l. Откуда следует, что уклон и интервал прямой - величины, обратные друг другу. Следствие: прямую линию в проекциях с числовыми отметками можно задать направлением ее проекции с проекциями одной точки и интервалом или уклоном (рис. 100). 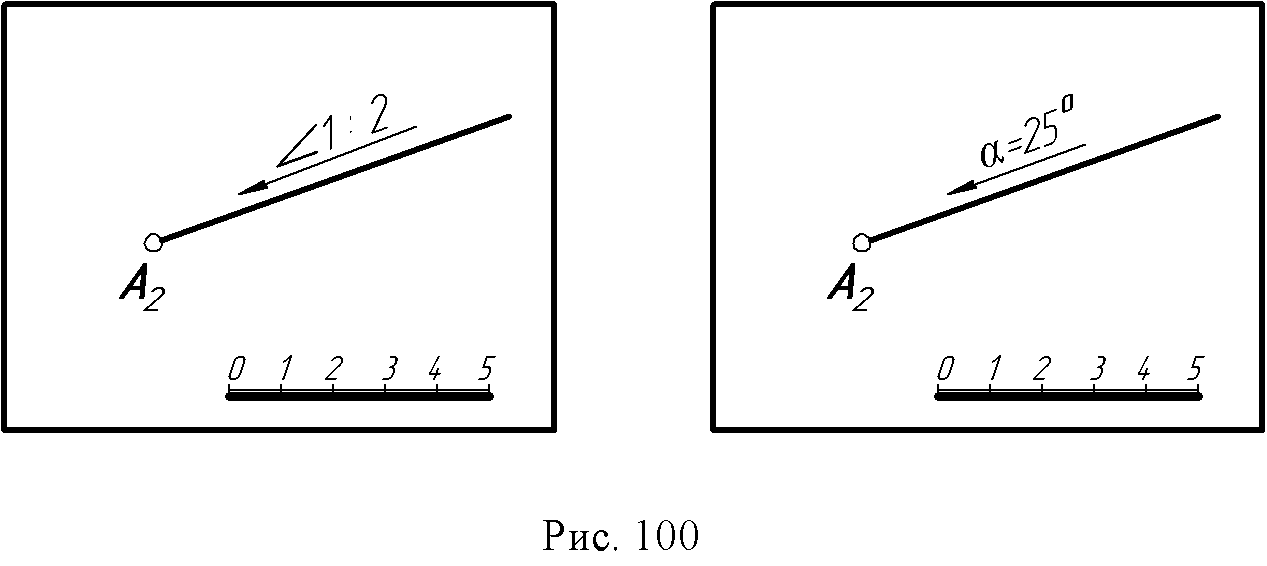 Проградуировать прямую - это значит, определить точки, отметки которых выражены целыми числами. Существует несколько способов градуирования прямой. 1 способ (рис. 101) - проведем через произвольные, но равные интервалы, параллельно отрезку АВ серию параллельных прямых; обозначим их как горизонтали с целыми отметками. На перпендикулярах, восстановленных к проекции прямой АВ из точек А5,8 и В3,5, отметим положение точек А1В1. Точки пересечения ее с построенными горизонталями дают положение искомых точек. 2 способ (рис. 101) - вариант решения задачи делением отрезка в заданном отношении по теореме Фалеса. 3 способ - аналитический - с помощью формул уклона и интервала прямой. Зная длину проекции прямой - заложение L (рис. 101) легко определить величину интервала из отношения: l = L/H, где Н - превышение точки В над точкой А. 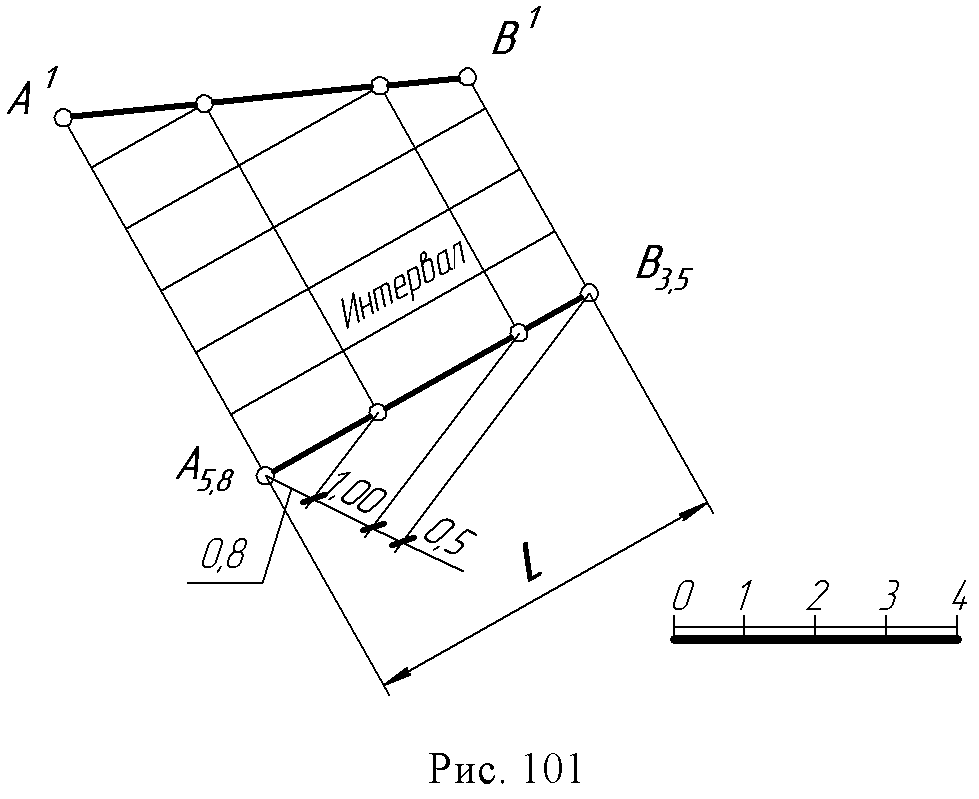 14.3. Взаимное положение двух прямых Параллельные прямые (рис. 102а). Две прямые параллельны между собой, если их проекции также параллельны, интервалы и уклоны равны и числовые отметки возрастают в одну и ту же сторону. ℓAB=ℓCD; ίAB=ίCD 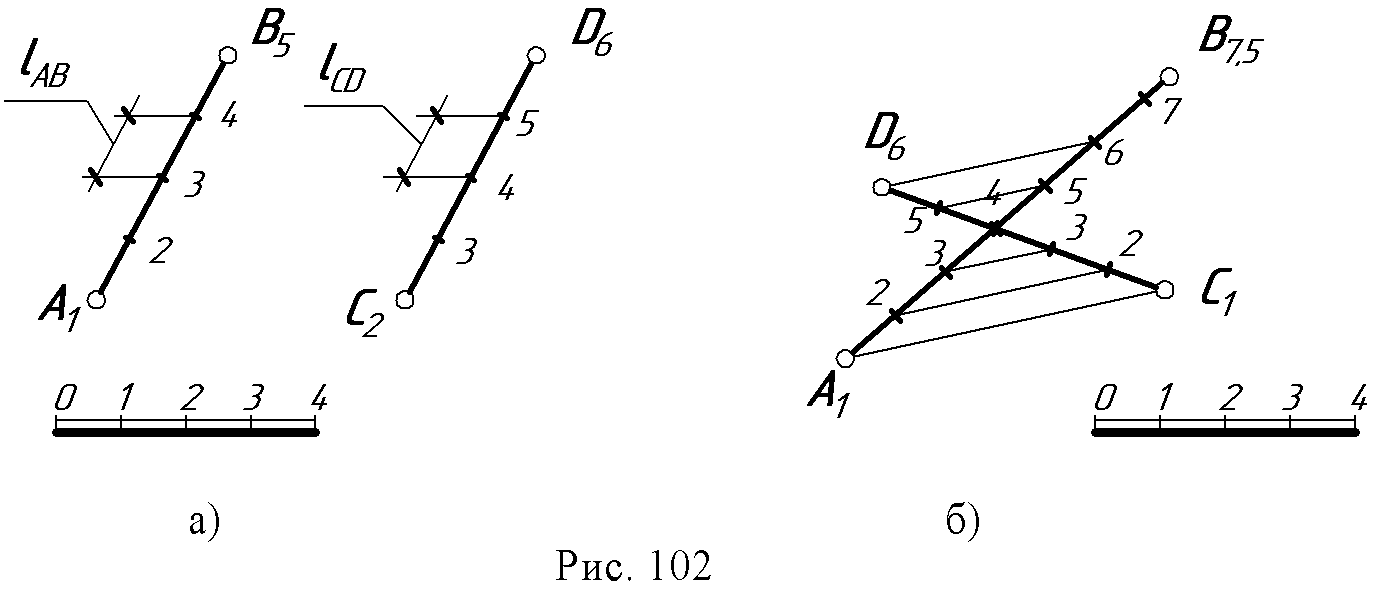 Пересекающиеся прямые (рис. 102б). Точка пересечения пересекающихся прямых имеет одинаковые отметки на первой и второй прямой. Это легко проверить, если прямые проградуированы: прямые, соединяющие точки с одинаковыми отметками, параллельны между собой. Скрещивающиеся прямые (рис. 102в). 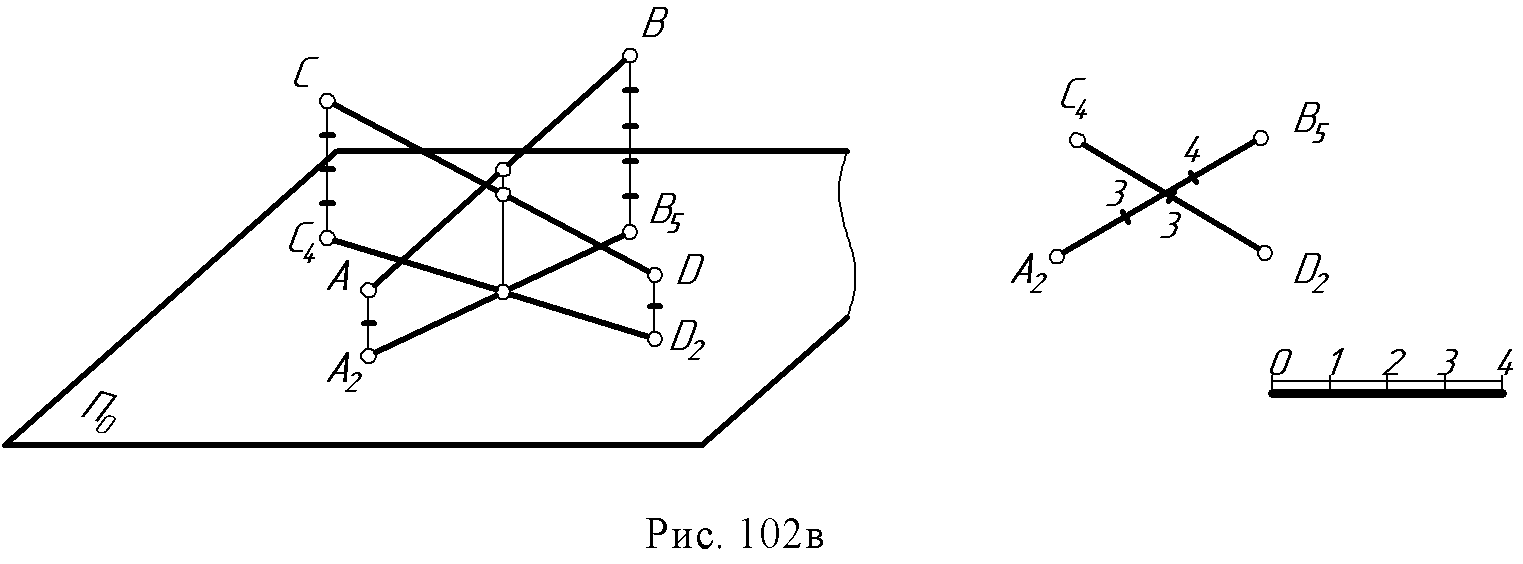 Если признаки параллельности и пересечения прямых отсутствуют, прямые скрещиваются. Отметки прямых в точке пересечения их проекций разные для каждой прямой. |
