Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия
 Скачать 1.98 Mb.
|
|
Вопросы для самопроверки.
6.1. Сущность способа. Сущность способа вращения состоит в изменении положения объекта, заданного на эпюре, таким образом, чтобы определенные его элементы заняли относительно плоскостей проекций частное положение и проецировались без искажения. Начиная преобразование этим способом, надо подготовить аппарат вращения: ось, центр и радиус вращения. По положению оси вращения различают несколько видов этого способа. Вращение вокруг оси, перпендикулярной плоскости проекций. При вращении точки в пространстве вокруг оси, перпендикулярной горизонтальной плоскости проекций, проекции точки перемещаются так: горизонтальная – по окружности, фронтальная – по прямой, параллельной оси проекций (или перпендикулярной оси вращения) (рис.40). 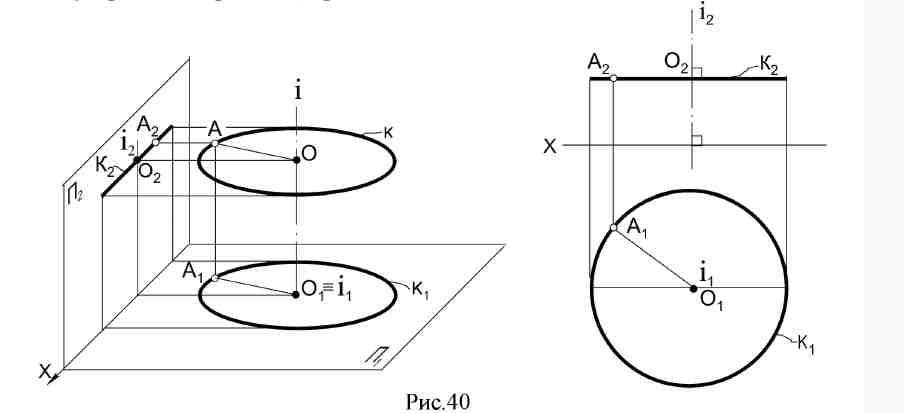 Если ось вращения перпендикулярна фронтальной плоскости проекций, то на эпюре получается обратная картина (рис.41). Чтобы повернуть вокруг оси прямую линию, достаточно вращать ее точки на один и тот же угол. При вращении плоскости следует вращать определяющие ее элементы: три точки, прямую и точку и т.д. Этим способом удобно определять натуральную величину отрезка прямой и угол наклона ее к плоскости проекций, при этом ось вращения рационально провести через одну из точек прямой линии, чтобы избежать лишних построений. 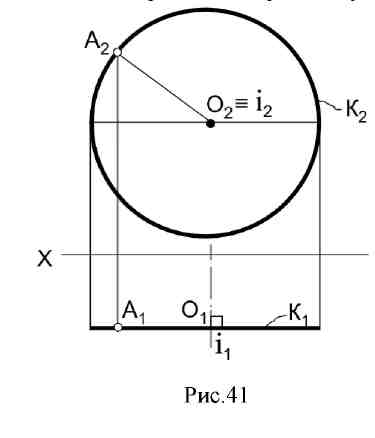 Определить натуральную величину отрезка прямой АВ (рис. 42) Чтобы прямая проецировалась в натуральную величину, она должна располагаться параллельно какой - либо плоскости проекций, а значит, одна ее проекция должна быть параллельна оси проекций: АВ || П1; Â2B2|| ОХ; ось вращения проходит через точку В; Â 1 B 1 - натуральная величина АВ. 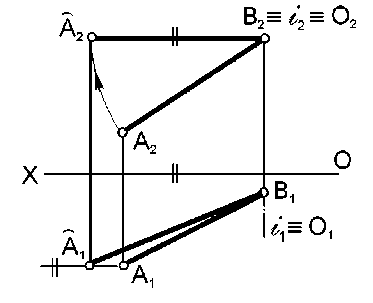 Рис. 42 6.2. Вращение вокруг горизонтали или фронтали. При вращении точки в пространстве вокруг горизонтали горизонтальная проекция точки перемещается по прямой, перпендикулярной проекции горизонтали, а фронтальная - по эллипсу (искаженной проекции окружности вращения). При решении задач этот эллипс не строится. Отрезок О1А0 – натуральная величина радиуса вращения точки А; отложив его на линии, перпендикулярной h1, мы точку перемещаем в плоскость, параллельную горизонтальной плоскости проекций П1(рис.43) 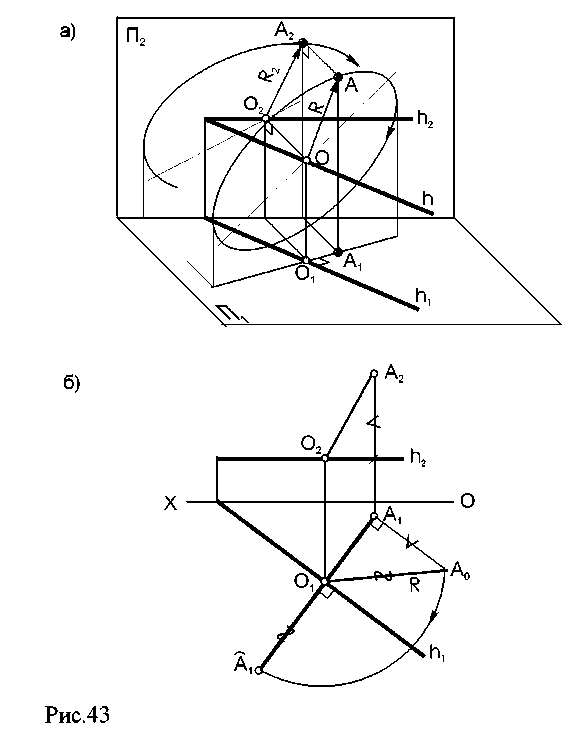 Пример: Определить натуральную величину треугольника АВС (рис. 44). 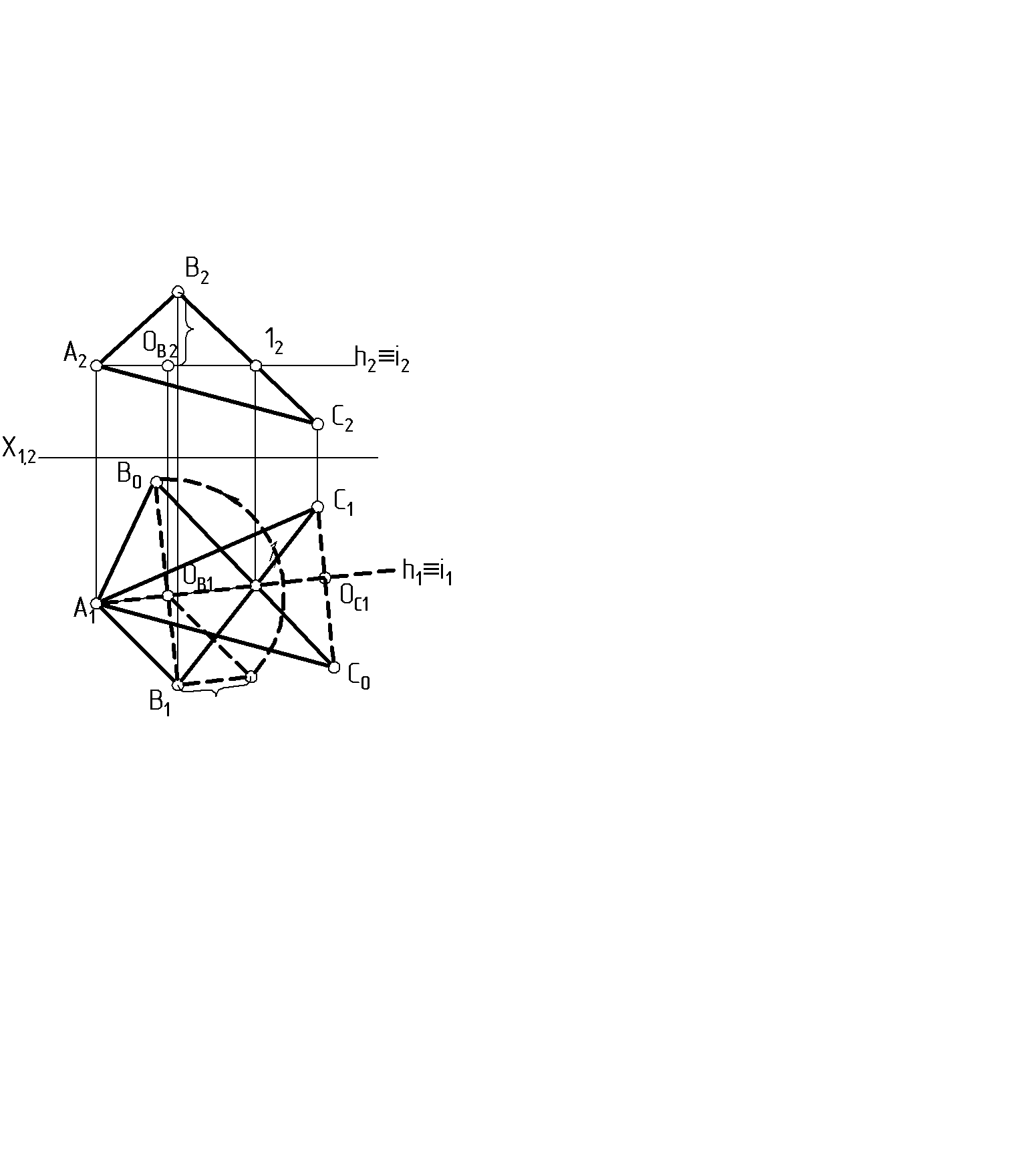 Рис. 44 За ось вращения i примем горизонталь h и повернем треугольник АВС вокруг нее как вокруг оси вращения до положения, параллельного плоскости П1; точки А и 1 остаются неподвижными, а В и С вращаются. Способом прямоугольного треугольника определяем натуральные величины радиусов вращения, а траектории движения на П1перпендикулярны линии i1. Новое положение точки С - С0 можно найти как пересечение двух траекторий вращения С1ОС1 и В011, которая уже лежит в плоскости, параллельной горизонтальной плоскости проекций. A1B0C0 – натуральная величина треугольника АВС. 6.3. Плоскопараллельное перемещение (вращение без указания оси). При вращении прямой линии, плоскости и любого другого объекта, их проекции на плоскости, перпендикулярной оси вращения, сохраняют свою величину и форму. Вторые проекции объекта перемещаются по прямым, перпендикулярным проекции оси вращения (или линиям связи). Эти свойства проекций позволяют перемещать данный объект в частное положение, используя свободное поле эпюра, без нанесения проецирующих осей вращения. 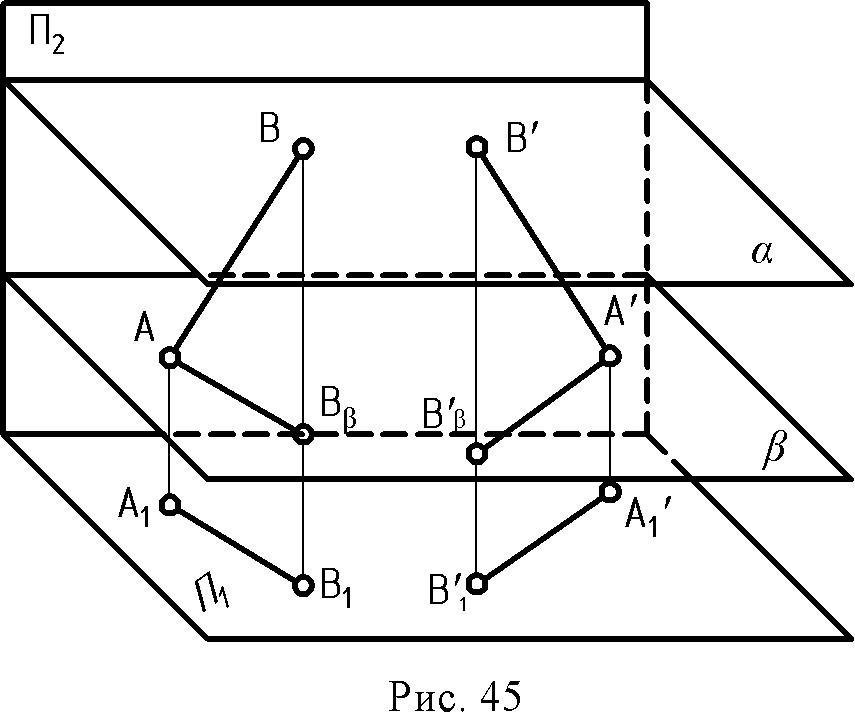 На рис. 45 отрезок АВ повернем на некоторый угол вокруг условной оси, перпендикулярной горизонтальной плоскости проекций. Из положения АВ он переместится в положение А1В1; горизонтальная проекция отрезка А1В1займет положение А11В11; |А1В1|= |А11В11|. Пример. Определить натуральную величину отрезка AB (рис. 46). Одна проекция отрезка AB должна быть расположена параллельно оси Х. Повернем A1B1, до такого положения, при этом фронтальные проекции точек переместятся по линиям, параллельным оси Х, сохраняя проекционную связь. Длина А21В21 равна натуральной величине отрезка AB.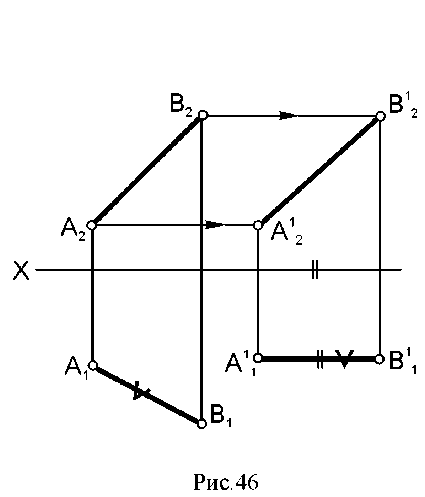 
7. Лекция 7. Кривые линии. Поверхности. 7.1. Общие положения. Классификация кривых линий. Кривой линией называется геометрическое место (непрерывное множество) последовательных положений точки, движущейся в пространстве. Кривые линии широко применяются в различных областях науки и техники, а также для образования поверхностей различных архитектурных деталей и конструкций, зданий и сооружений. Кривые линии по положению точек в пространстве делятся на два вида:
К  ривые линии подразделяются и по другим признакам. Кривая может быть описана аналитически, т.е. уравнением (алгебраическим или трансцендентным), например эллипс, парабола, синусоида и т.д. Если образование кривой не имеет строгой закономерности, то она задается графически, например, горизонтали на плане местности. Степень уравнения, которое выражает алгебраическую кривую, определяет порядок кривой. Геометрически порядок плоской кривой определяется числом ее точек пересечения прямой линией. Примером может служить эллипс, его уравнение - это аналитически; геометрически: следовательно, эллипс - кривая второго порядка. Порядок пространственной кривой определяется числом точек пересечения кривой с плоскостью. Кривая т - кривая четвертого порядка (рис. 47). 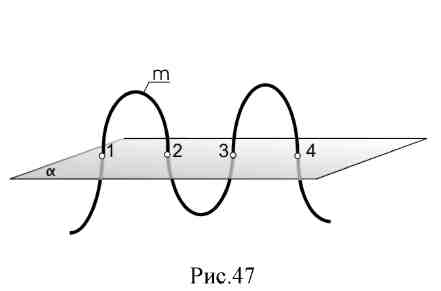  7.2. Особые точки плоских кривых. Точки перегиба (н) - точки, в которых кривая проходит на другую сторону касательной прямой, сохраняя касание. Двойная или узловая точка (А) - это точка, в которой кривая пересекает сама себя. В точке А кривая имеет две различные касательные t1и t2. Точки возврата первого ряда (В), в которой кривая подходит к точке двумя ветвями, имеющими в точке В общую касательную, расположенными по разные стороны от касательной. Точки возврата второго ряда С, в которой кривая подходит к точке двумя ветвями, имеющими в точке С общую касательную, расположенными (вблизи точки С) по одну сторону от обеих ветвей кривой. Все точки кривых сохраняют свои особенности при параллельном проецировании. В начертательной геометрии кривые линии изучаются по их проекциям. Свойства проекций кривой:
7.3. Плоские кривые. Наиболее распространенными являются плоские кривые линии. Касательной в плоскости кривой в некоторой ее точке называется предельное положение секущей, когда две общие с кривой точки сечения, стремясь, друг к другу, совпадут. Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке ее касания. Секущая и касательная проецируются в секущую и касательную к проекции кривой (рис. 48). 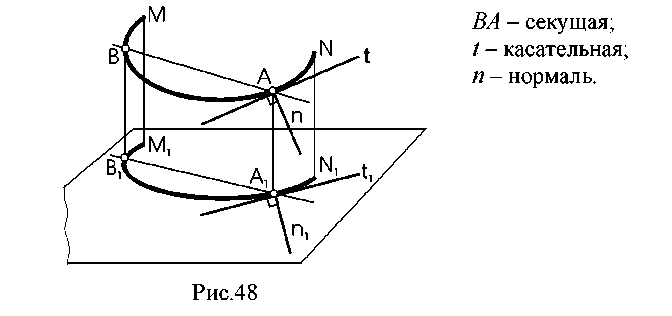 7.4. Поверхности. Общие положения. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых устанавливается определенная зависимость. В начертательной геометрии поверхность рассматривается как непрерывное множество последовательных положений линии, перемещающейся в пространстве по определенному закону. Такой способ называется кинематическим. Линию l, которая при своем движении образует поверхность, называют образующей. Образующая может перемещаться по какой-либо другой неподвижной линии m , называемой направляющей (рис. 49). 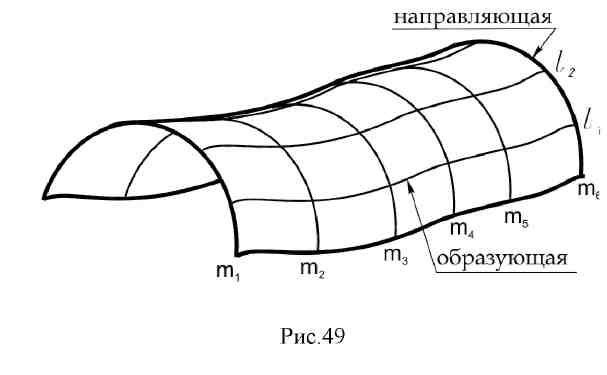 Способы задания поверхности на чертеже: 1. Каркас - это сеть линий, состоящая из двух семейств: семейства образующих l112, ...и семействами направляющих т1,т2… Каждая линия одного семейства пересекает все линии второго семейства (рис. 50). 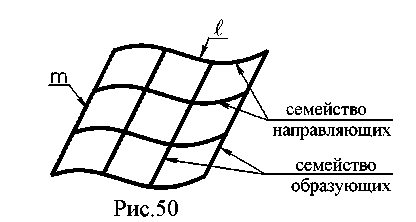 2. Очерк - проекция линии контура поверхности (рис. 51). 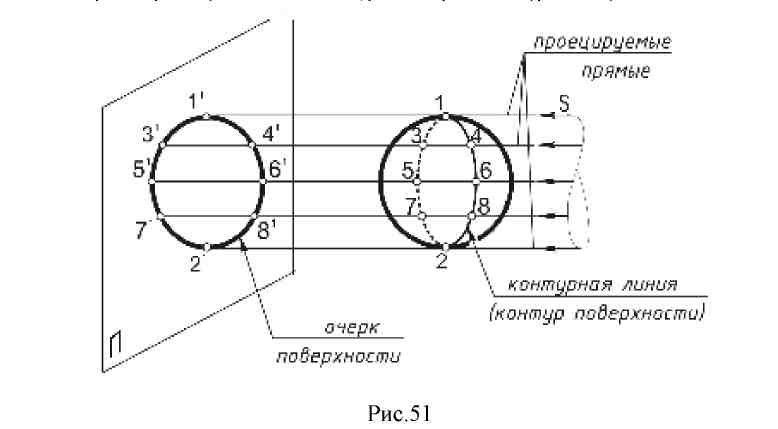 Контуром поверхности называется линия, точки которой являются точками касания к поверхности проецирующих. При изображении поверхности на чертеже проекцию контурной линии (очерк) называют еще линией видимости, которая является границей, отделяющей видимую часть поверхности от невидимой.
 Из сказанного выше можно сделать следующий вывод: поверхность считается заданной, если относительно любой точки пространства однозначно решается вопрос о принадлежности ее к данной поверхности. 7.5. Классификация поверхностей. По виду образующей:
По закону движения образующей: (т.е. по направляющей)
7.6. Линейчатые поверхности. Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим. Возьмем в пространстве три кривые линии l. 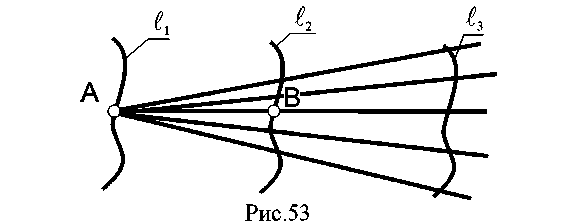 Пусть прямая движется так, что в любом своем положении она пересекает все три кривые l1 l2, l3, тогда при своем движении они описывают линейчатую поверхность (рис. 53). Выберем на направляющей l1точку А. Через нее мы сможем провести бесчисленное множество прямолинейных образующих, пересекающих направляющую l3. Этим самым определяется коническая поверхность с вершиной в точке А. В какой - то момент образующие пересекут линию l2 - это точка В, в которой коническая поверхность пересечет линию l2. В зависимости от вида направляющих получаются различные поверхности. Поверхности с одной направляющей: 1. Коническая - образуется движением прямой линии l (образующей) по некоторой кривой линии m и имеющей неподвижную точку S (рис. 54). 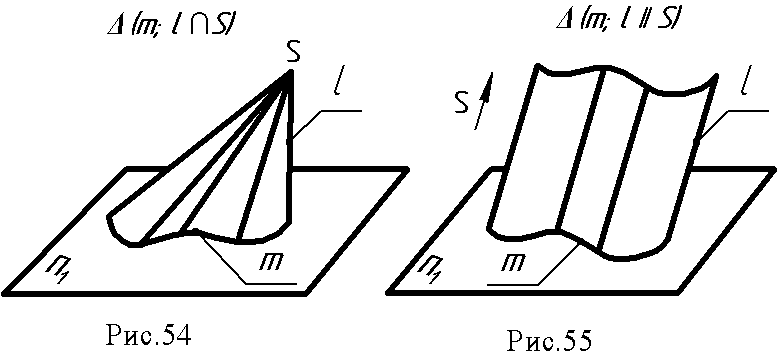 2. Цилиндрическая поверхность образуется движением прямой l (образующей) по некоторой кривой т параллельно самой себе или имеющей постоянное направление S ∆(т,1|| S) (рис. 55). 3. Торсовая поверхность образуется движением прямой l, касающейся во всех своих положениях некоторой пространственной направляющей кривой т, называемой ребром возврата ∆ (т,l) (рис.56). 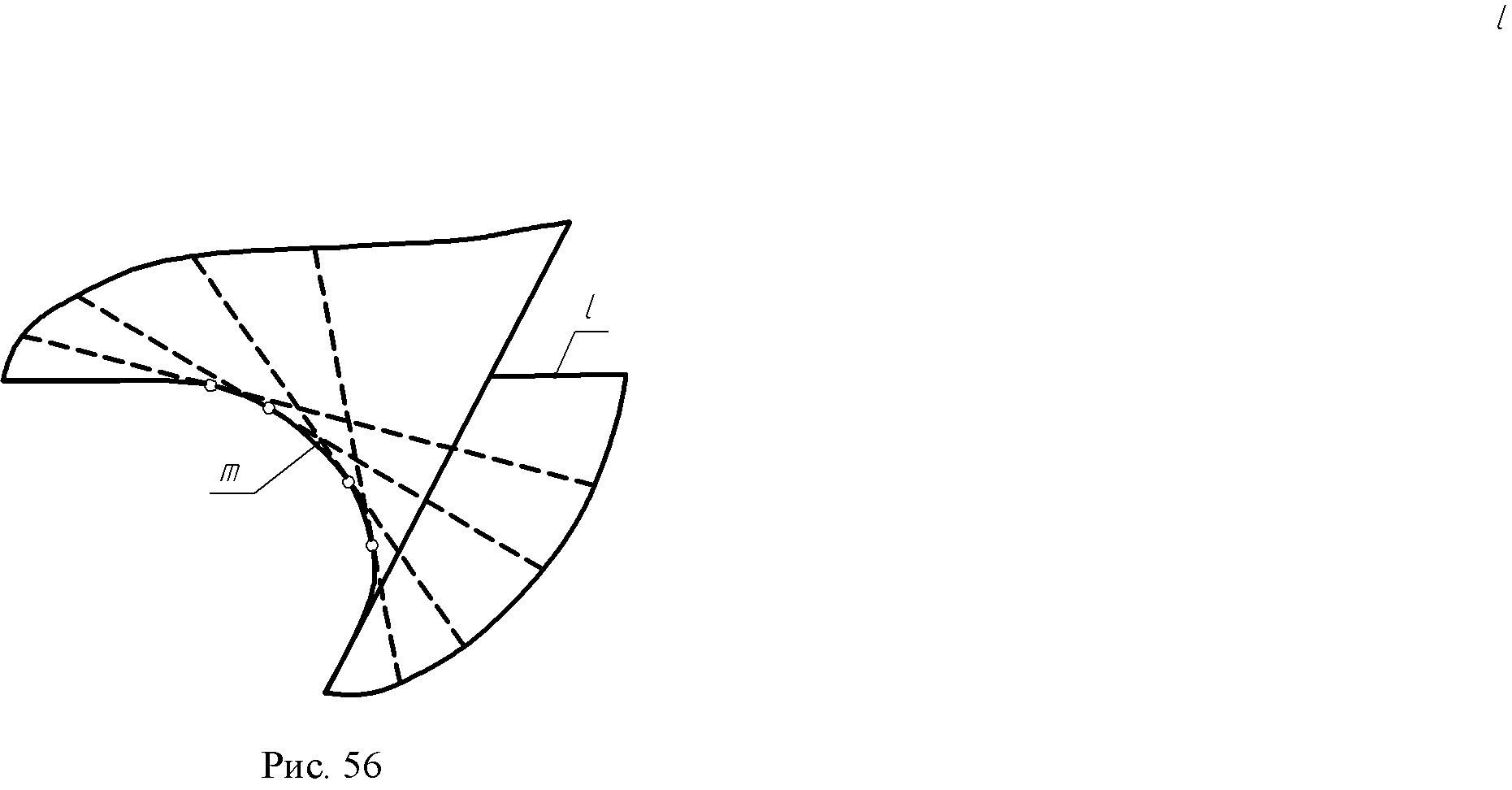 4. Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей. 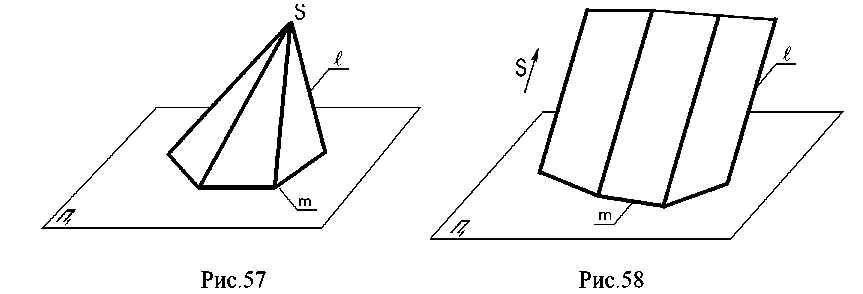 Если направляющая т ломаная, а все образующие l пересекаются в одной точке, такая поверхность называется пирамидальной (рис. 57); если все образующие параллельны - поверхность называется призматической (рис. 58). Многогранником называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников. Отсеки плоскостей называются гранями, а линии их пересечения - ребрами. Точки пересечения ребер называются вершинами. 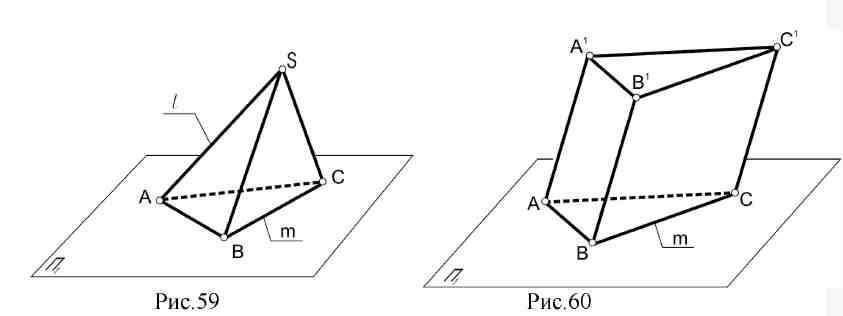 Поверхность с замкнутой ломаной направляющей (m), общей точкой пересечения образующих ребер и граней называется пирамидой (рис.59). Поверхность с замкнутой ломаной направляющей (m) (основанием) и взаимно параллельными ребрами - призма (рис.60). Если ребра призмы перпендикулярны основанию, гранник называется проецирующей призмой (рис.61).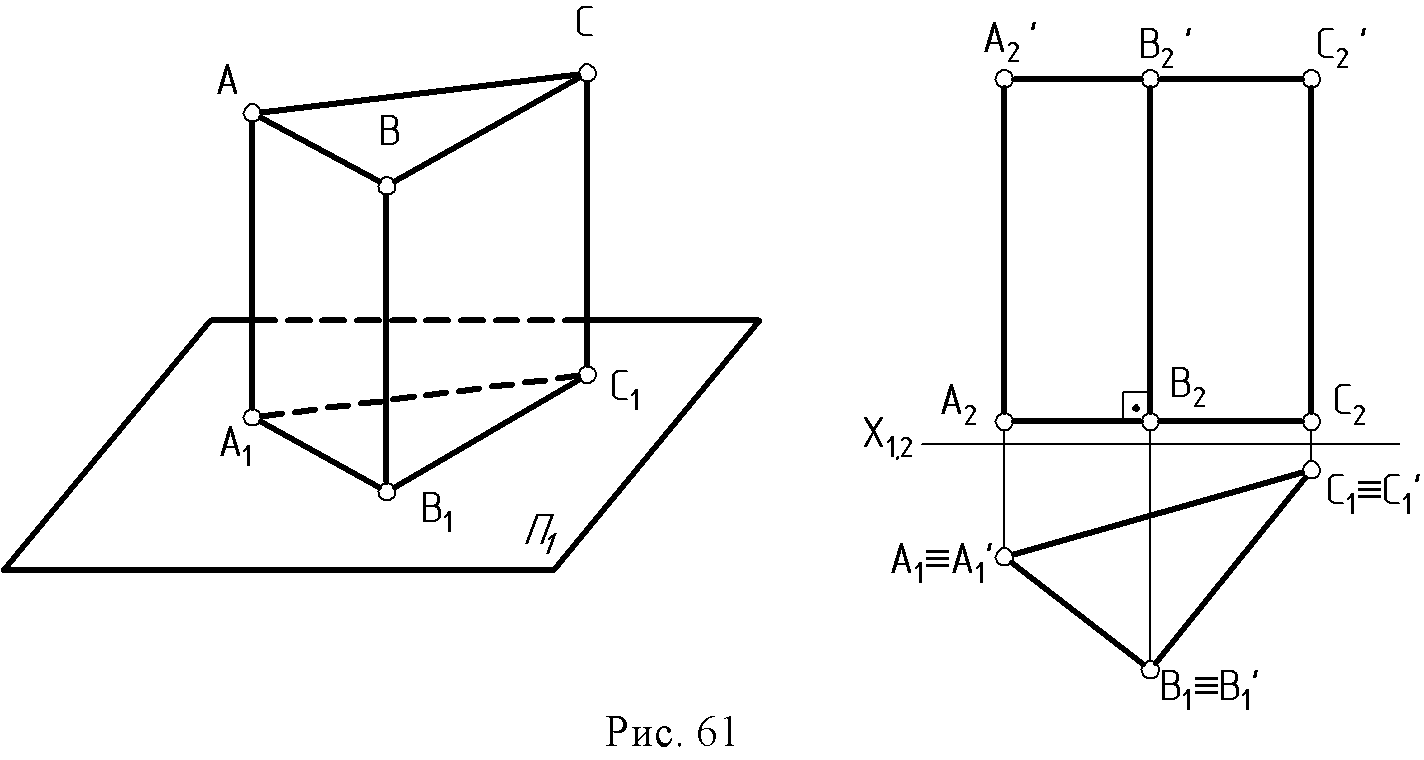 
8. Лекция 8. Поверхности. 8.1. Линейчатые поверхности с двумя направляющими (поверхности Каталана) У этих поверхностей все образующие параллельны неподвижной плоскости, называемой соответственно плоскостью параллелизма. 1. Цилиндроид (l, m, n; П2), (l//П2) - поверхность, образованная движением прямой образующей l по двум криволинейным направляющим m и n; все образующие параллельны плоскости параллелизма П2(рис. 62). 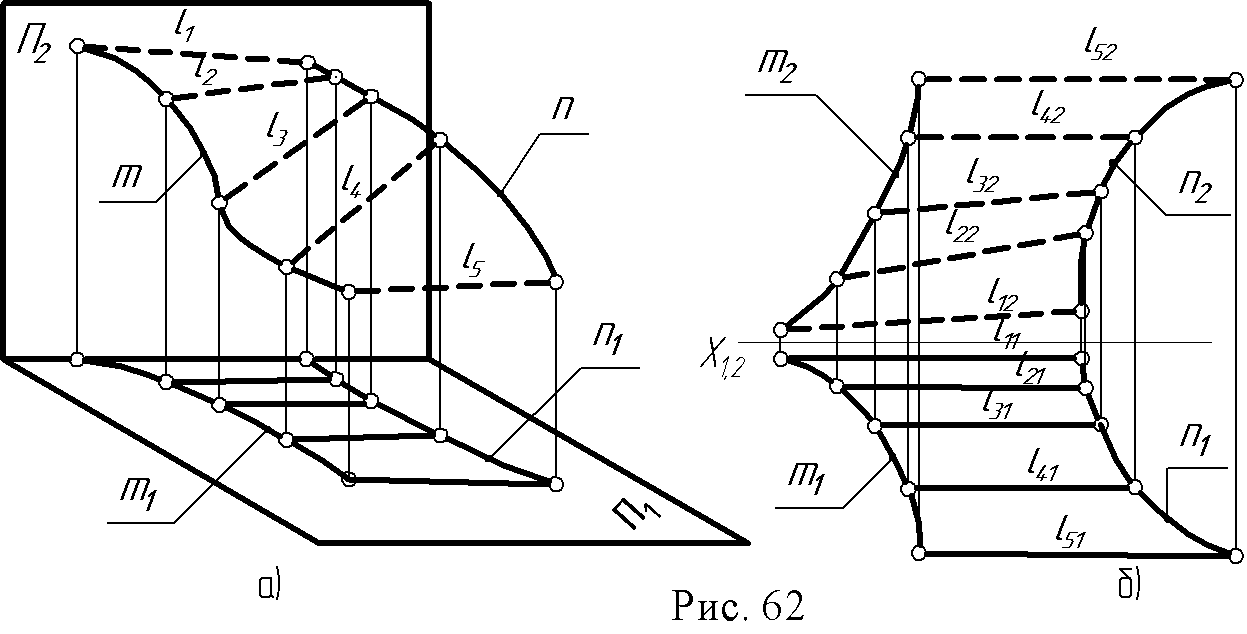 2. Коноид - поверхность, образованная движением прямолинейной образующей по двум направляющим, одна из которых прямая, другая - кривая линия (рис.63). Все образующие параллельны некоторой плоскости П1; )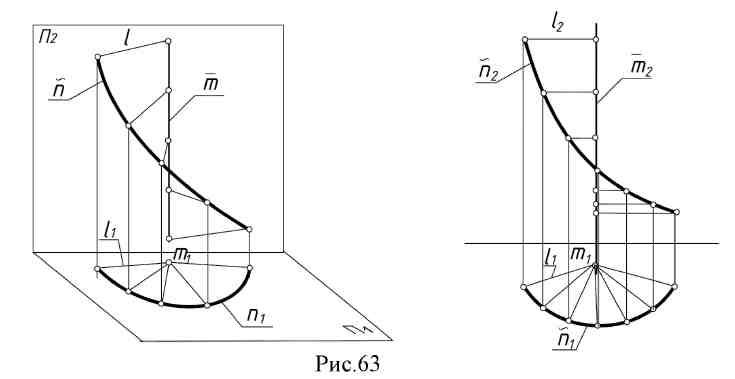  
∆(m, n, П1, l) (m ●n; l // П1) 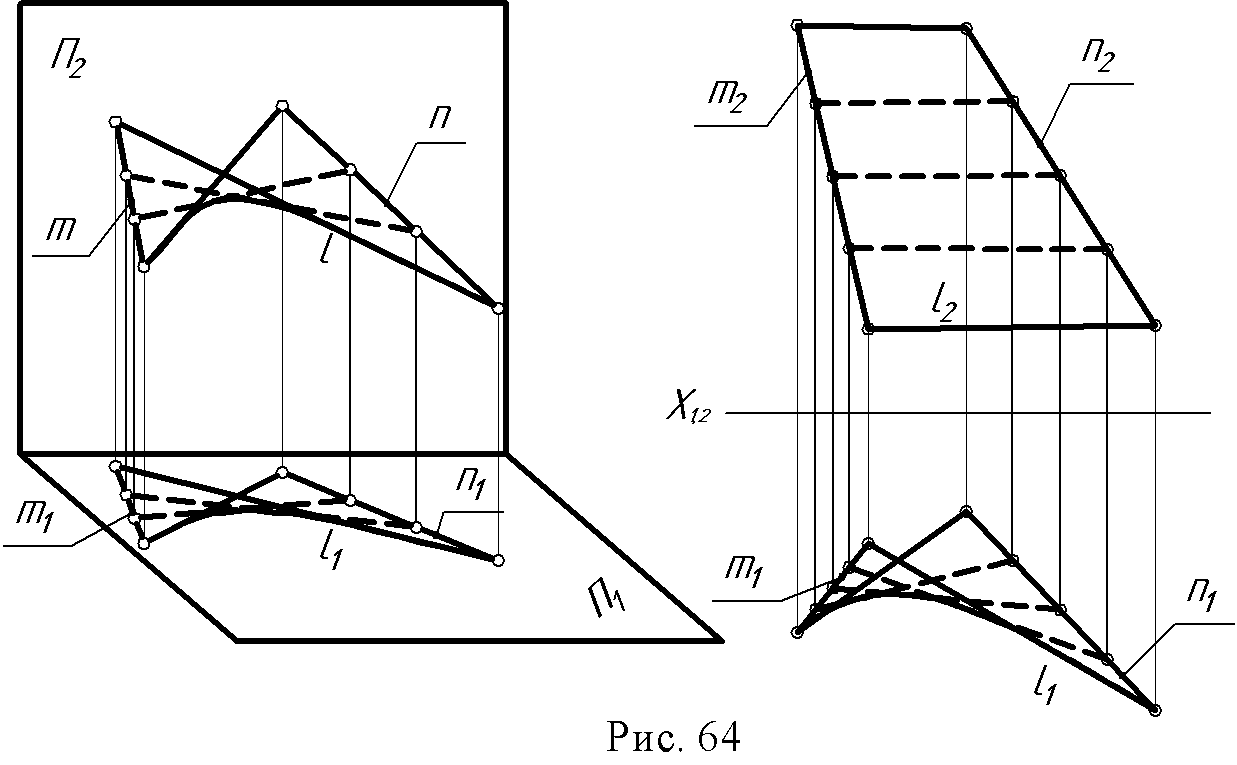 |