Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
1. Содержание и задачи курса начертательной геометрии.Трудно указать такой вид человеческой деятельности, где, решая ту или иную техническую или нетехническую задачу, не приходилось бы прибегать к помощи изображений машин и механизмов, планов строений и т.п. Различны требования, предъявляемые к форме и содержанию изображений. Одни из них должны производить на глаз человека такое же впечатление, какое производит и сам изображаемый предмет, иначе говоря, изображение должно обладать достаточной наглядностью. В другом случае изображение должно быть, в первую очередь, геометрически равноценно оригиналу, оно должно давать полную геометрическую и размерную характеристику изображаемого предмета. Этому требованию должен отвечать, например, всякий машиностроительный чертёж. Наконец, к изображению могут быть предъявлены оба указанных условия одновременно - наглядность изображения должна сочетаться с геометрической равноценностью оригиналу. Изображения различных предметов и объектов не являются самоцелью, они дают возможность решать инженеру по ним различные технические задачи. Однако не всякое изображение может быть использовано для решения технических задач. Для этого оно, в первую очередь, должно быть геометрически равноценно изображаемому объекту, то есть, построено по определённому геометрическому закону. Вопросами исследования геометрических основ построения изображений предметов на плоскости, вопросами решения пространственных геометрических задач при помощи изображений занимается НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ. Методы начертательной геометрии находят самое широкое применение в объектах изучения самой различной природы: в механике, архитектуре и строительстве, химии, геодезии, геологии, кристаллографии и т.д. Но наибольшее значение и применение методы начертательной геометрии нашли в различных областях техники при составлении различного вида технических чертежей: машиностроительных, строительных, различного рода карт и т.д. Начертательная геометрия входит в группу общетехнических дисциплин, составляющих основу всякого инженерного образования. Она учит грамотно владеть выразительным техническим языком - языком чертежа, умению составлять и свободно читать чертежи, решать при помощи чертежей различные инженерно-технические задачи. Кроме того, изучение начертательной геометрии способствует развитию у студентов пространственных представлений и пространственного воображения - качеств, характеризующих высокий уровень инженерного мышления и необходимых для решения прикладных задач. В процессе изучения начертательной геометрии достигаются и другие цели, расширяется общенаучный кругозор студентов, развиваются навыки логического мышления, внимательность, наблюдательность, аккуратность и другие качества, развитие которых является одной из задач обучения и воспитания в высшей технической школе. Предметом начертательной геометрии (в узком смысле) является изучение теории построения плоских моделей пространств и теории и практики решения пространственных задач на таких плоских моделях. Цели курса:
2. Краткая история разработки и развития методов изображений.Сведения и приёмы построений, обуславливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно с древних времён. В течение продолжительного периода плоские изображения выполнялись как изображения наглядные. С развитием техники первостепенное значение приобрёл вопрос о применении метода, обеспечивающего точность и удобство измерений изображений, т.е. возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путём простых приёмов определить размеры отрезков линий и фигур. Постепенно накопившиеся отдельные правила и приёмы построения таких изображений были приведены в систему и развиты в труде французского учёного Монжа, изданном в 1799 году. Изложенный Гаспаром Монжем (1746-1818) метод - метод ортогонального проецирования - обеспечивал выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остаётся основным методом составления технических чертежей. Чертёж - язык инженера, начертательная геометрия - грамматика этого языка. В России начертательную геометрию начали преподавать с 1810 года в первом ВУЗе страны, только что организованном. Лекции там читал Я.А. Севастьянов (1796-1849), с именем которого связано появление первого оригинального труда под названием "Основания начертательной геометрии" (1821 г.), в основном посвящённого изложению метода Монжа. Крупный след в развитии начертательной геометрии в России в XIX веке оставили Н.И. Макаров (1824-1904) (адмирал Макаров, погибший в Порт-Артуре) и В.И. Курдюмов (1853-1904). Если начертательная геометрия как предмет возникла из нужд практики и в середине XIX века она расширила свои разделы, то к началу XX века аналитические методы, применённые в начертательной геометрии, вышли на первый план, точность графических методов не удовлетворялась и начертательная геометрия пошла на убыль. Последними книгами были книги Н.А. Рынина (1877-1942) и В.О. Гордона. С появлением трудов Н.Ф. Четверухина (1891-1973) начертательная геометрия была выведена из застоя. Н.Ф. Четверухин стал рассматривать начертательную геометрию как самостоятельную науку (не связанную с черчением). Он первый увидел, что методами начертательной геометрии можно решать сложные конструктивные задачи. Появилась "Прикладная геометрия" и начался её расцвет. За период с конца 40-х годов начертательная геометрия развивалась и расширялась. В науке большая роль принадлежит И.И. Котову (1905-1975) и его ученикам. Основателем украинской школы начертательной геометрии в теории изображений считается профессор С.М. Колотов. Принятые обозначения
а) совпадение двух геометрических образов ≡ например a≡b, А1≡B1; б) взаимная принадлежность геометрических образов , например А а, а а, Bβ. в) пересечение двух геометрических образов ∩, например t ∩ α, α ∩ β ; г) результат геометрической операции =, например К = l ∩ α . 6. Способ задания геометрического образа указывается в скобках рядом с его буквенным обозначением. Например: а(А, В) - прямая задана двумя точками Аи В; α (А, В, С) - плоскость задана тремя точками А, В, С; β (а, А) - плоскость задана прямой аи точкой А; γ (а∩b) - плоскость задана пересекающимися прямыми аи b; δ (l║ т) - плоскость задана параллельными прямыми l и т.
Прямой угол обозначается точкой внутри сектора.
а) линии уровня: горизонталь - h, фронталь -f; б) следы плоскости обозначаются той же буквой, что и плоскость, с добавлением подстрочного индекса, соответствующего плоскости проекций –аП2,βП1; в) линии уклона - и, касательная прямая - t, нормаль - п, оси вращения – i, j; 9. Последовательность геометрических образов - надстрочным индексом: точек - А1, А2, А3…; прямых - а1, а2, а3…; плоскостей - α1, α2, α3...
горизонтальная - П1; фронтальная - П2; профильная - П3.
на плоскости П1– А1, a1, α1; на плоскости П2 - А2, а2 , α2; на плоскостиП3 - А3, а3, α3.
1. Лекция 1. Метод проекций. Эпюр Монжа. 1.1. Виды проецирования. Начертательная геометрия представляет собой раздел геометрии, в котором геометрические свойства предметов материального мира изучаются при помощи их изображений на плоскости. В основу построения любого изображения положена операция проецирования, которая заключается в следующем. В пространстве выбирают произвольную точку S в качестве центра проецирования (рис. 1) и плоскость П1, не проходящую через точку S, в качестве плоскости проекций. Чтобы спроецировать точку А пространства на плоскость П1, через центр проецирования Sпроводят луч SA до его пересечения с плоскостью П1 в точке А1. Точку А1принято называть центральной проекцией точки А, а луч SA — проецирующим лучом. Широкое применение в практике получил тот случай, когда центр проецирования удален в бесконечность. Проецирующие лучи при этом параллельны между собой и проекции точек, фигур и тел получают название параллельных проекций (рис. 2). Проекцией точки А называют точку А1пересечения проецирующего луча АА1с плоскостью проекций. В свою очередь, параллельные проекции подразделяются на косоугольные и прямоугольные. В первом случае плоскость проекций с направлением проецирования образует угол, не равный 90°, во втором — этот угол равен прямому. 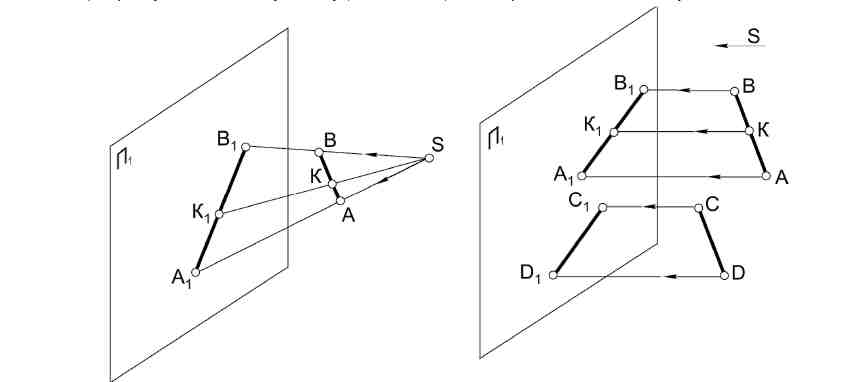 Рис.1 Рис.2 Проекция прямой линии представляет собой совокупность проекций точек этой линии. Такое геометрическое толкование процесса образования изображений соответствует явлениям, имеющим место в природе. Изображения, получающиеся на сетчатке глаза или на пластинке фотоаппарата, являются центральными проекциями с полюсами в оптическом центре глаза или объектива. Тени, падающие от предметов, освещенных солнцем, представляют параллельные проекции этих предметов, так как центр проекций – солнце, практически можно считать бесконечно удаленной точкой. Очевидно, что изображения, выполненные по способу центрального проецирования, обладают большей наглядностью, чем параллельные проекции, потому что в основе процесса зрения лежит центральное проецирование. Центральные проекции используются там, где от изображения в первую очередь, требуется наглядность. Параллельные проекции более удобны, когда необходимо получить изображение с возможно меньшими метрическими искажениями. При параллельном проецировании удается, например, получить проекцию отрезка прямой линии или плоской фигуры в натуральную величину и поэтому они находят наибольшее применение в технике и инженерном деле. 1.2. Свойства (инварианты) центральных проекций:
1.3. Свойства (инварианты) параллельных проекций: Рассмотренные выше 1, 2, 3 свойства центральных проекций присущи и параллельным проекциям, однако есть некоторые свойства только параллельных проекций: 4. Проекции параллельных прямых параллельны: АВ || СD А1В1|| С1D1(рис.2) 5. Проекции отрезков параллельных прямых пропорциональны самим отрезкам, т.е. 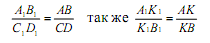 6. Если отрезок параллелен плоскости проекций, то длина проекции равна длине самого отрезка. Чертеж, полученный в результате центрального или параллельного проецирования, называется проекционным чертежом. Он должен быть:
|
