Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
8.2. Поверхности вращения. Поверхностью вращения называется поверхность, образованная вращением образующей вокруг неподвижной прямой оси. Образующая может иметь любой вид. При вращении каждая точка образующей совершает движение по окружности, которая лежит в плоскости, перпендикулярной оси вращения (оси поверхности) и с центром на этой оси. Окружности, по которым перемещаются все точки образующей, называются параллелями; наибольшую параллель называют экватором, наименьшую – горловиной (рис.65). Если ось поверхности вертикальна, то все параллели проецируются на горизонтальной проекции без искажения и наоборот. Плоскости, проходящие через ось вращения, пересекают поверхность по линиям, называемым меридианами. Меридиан, расположенный в плоскости, параллельной плоскости проекций, называется главным и проецируется на эту плоскость проекций очерком поверхности. 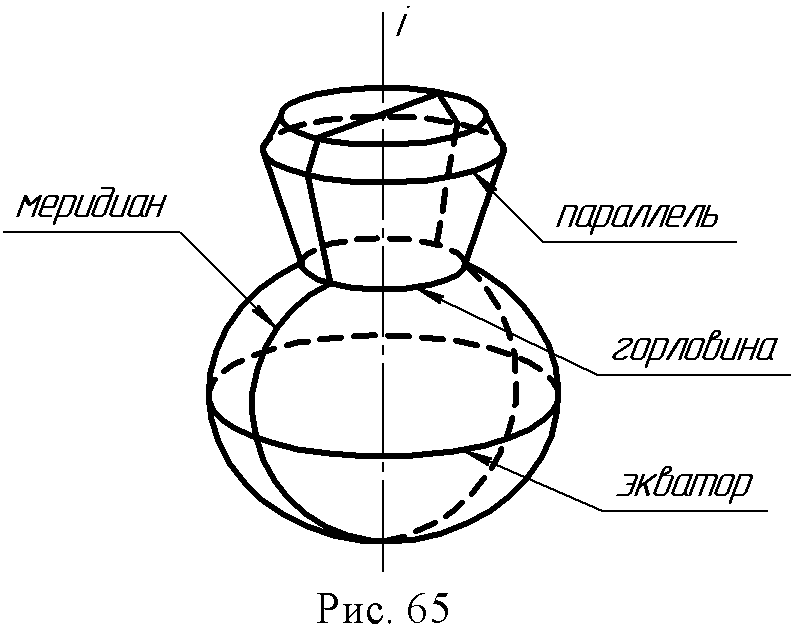 Поверхности, образованные вращением прямой линии - рис. 66, а, б, в.
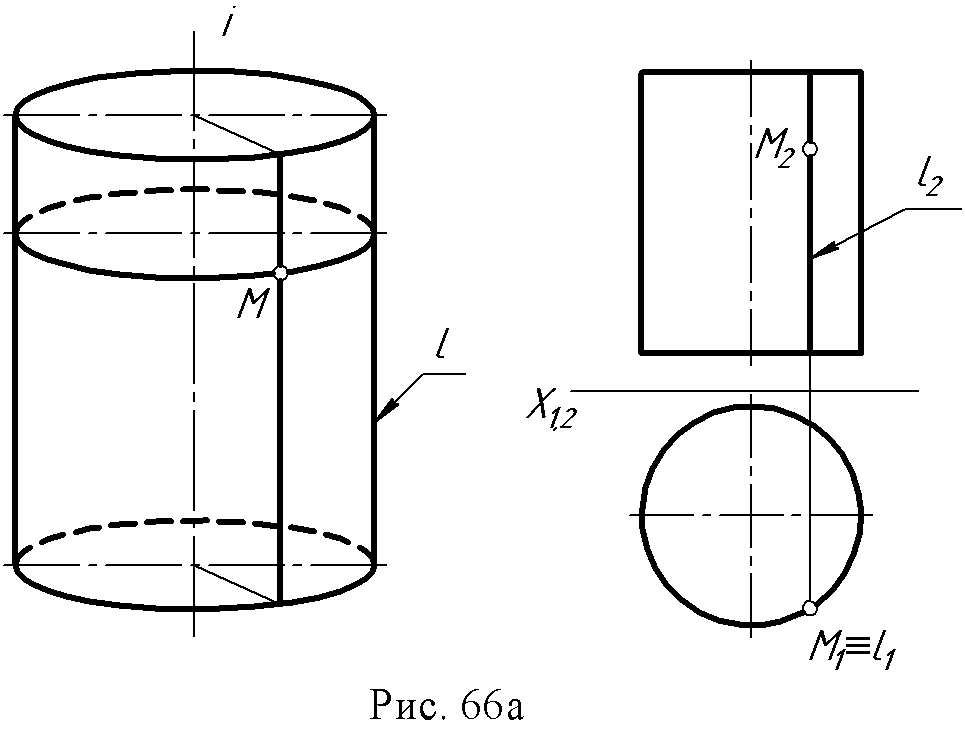 2. Конус вращения: образующая и ось - пересекающиеся в точке S прямые ∆ (i, l∩ i). 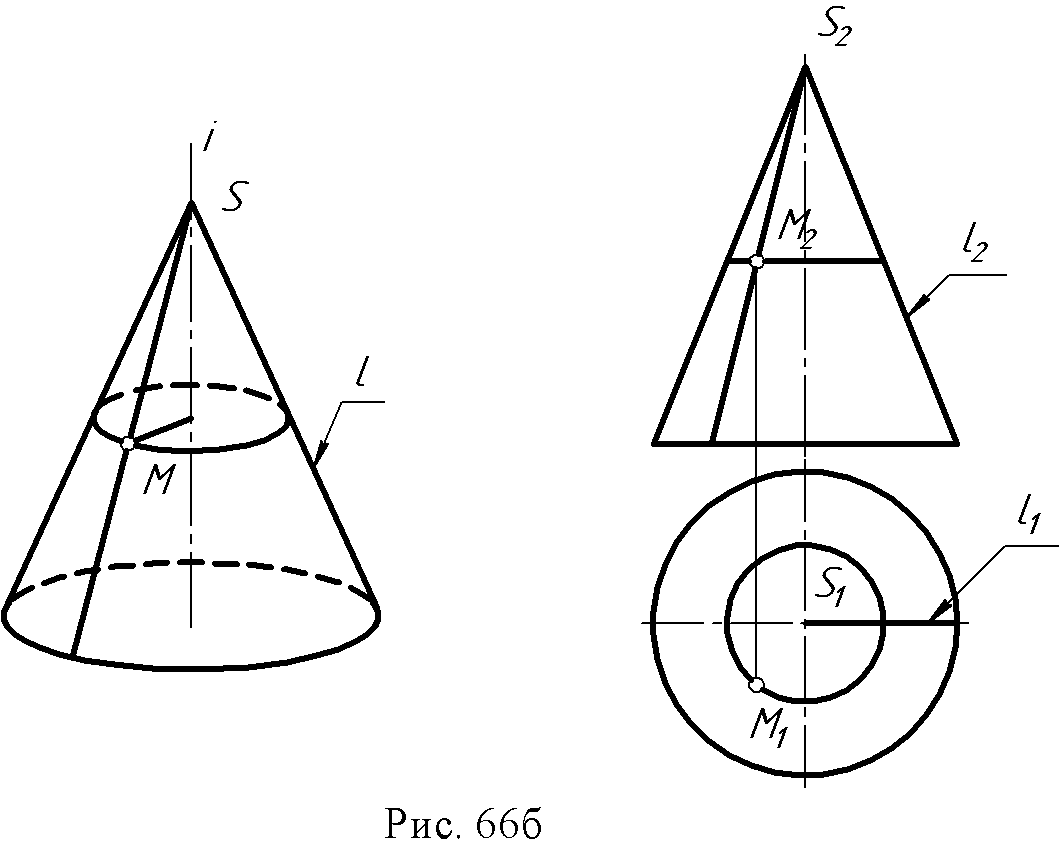 3. Однополостный гиперболоид вращения: образующая и ось – скрещивающиеся прямые ∆ (i, l ● i). 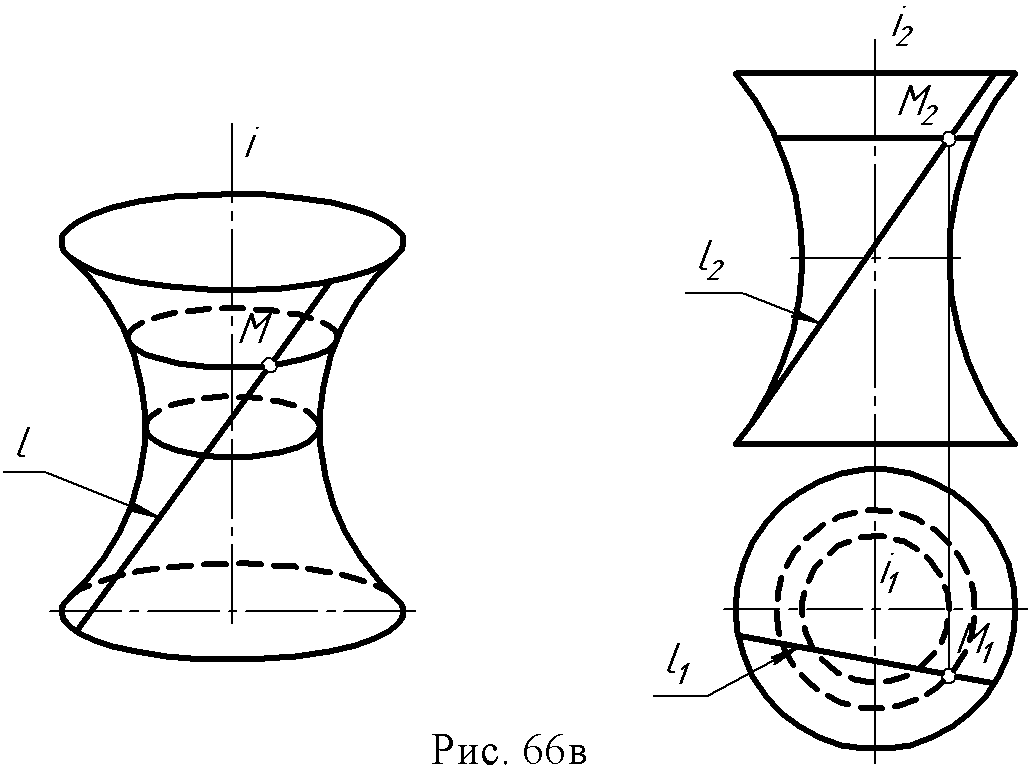 Поверхности, образованные вращением окружности (рис. 67 а, б): 1. Сфера образуется вращением окружности вокруг одного из диаметров. 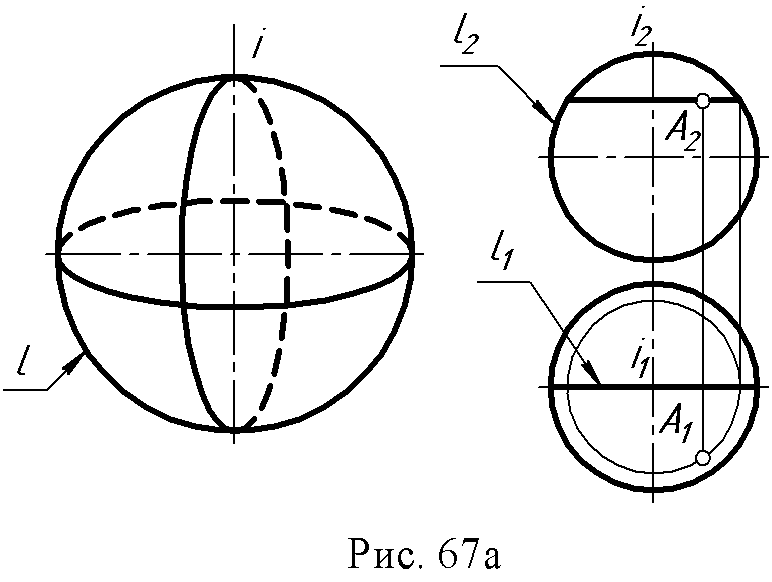 2. Тор образуется вращением окружности вокруг оси i, лежащей в плоскости окружности, но не проходящей через ее центр. 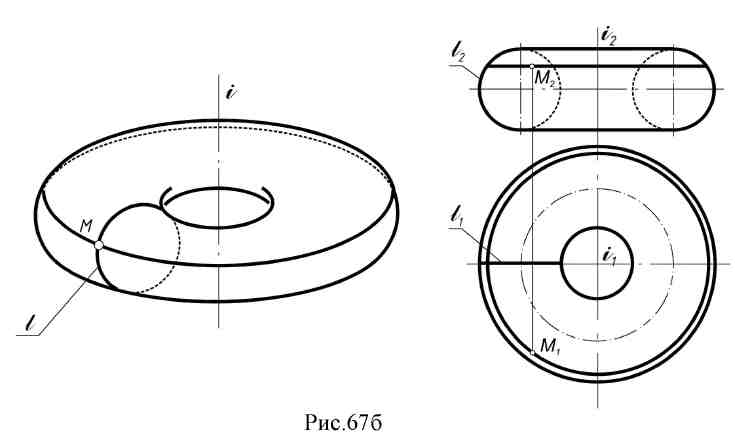 Если ось вращения не пересекает (образующую) окружность, получается поверхность открытого тора, если пересекает – закрытого или самопересекающегося. Поверхности, образованные вращением дуги окружности (рис. 68 а, б): 1. Выпуклый тор. 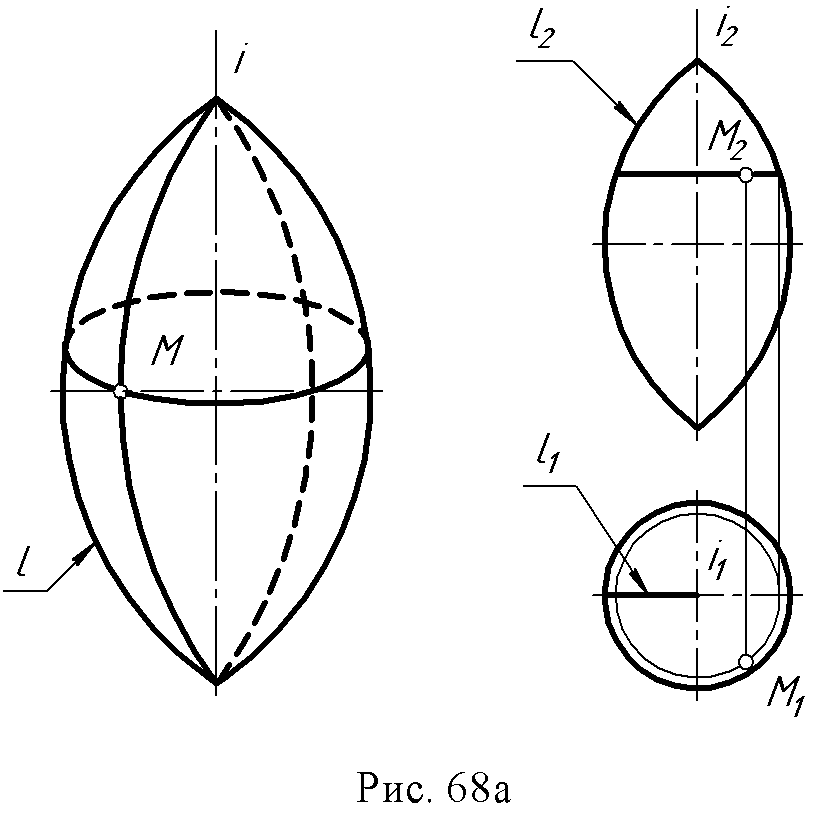 2. Вогнутый тор. 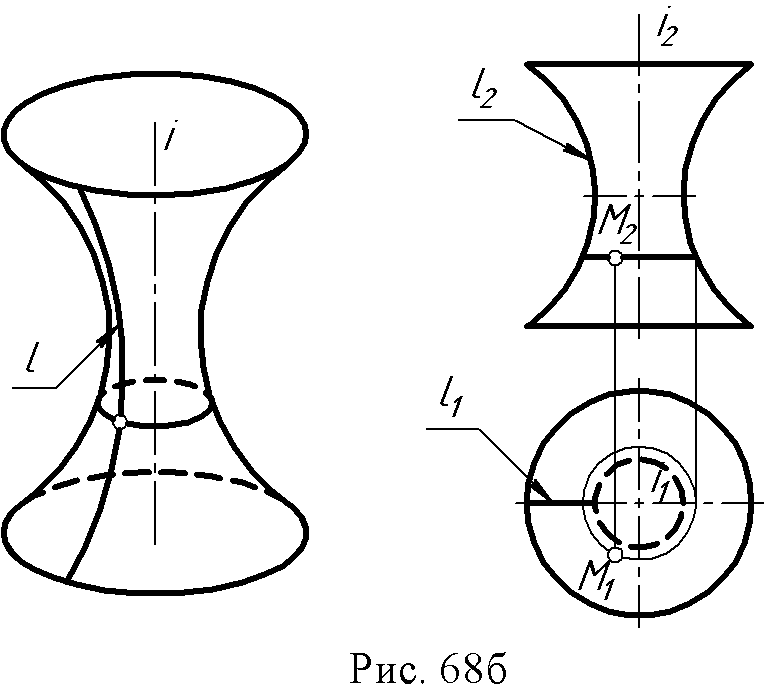 Поверхности, образованные вращением кривых второго порядка (рис. 69, а, б, в, г): 1. Эллипсоид вращения. 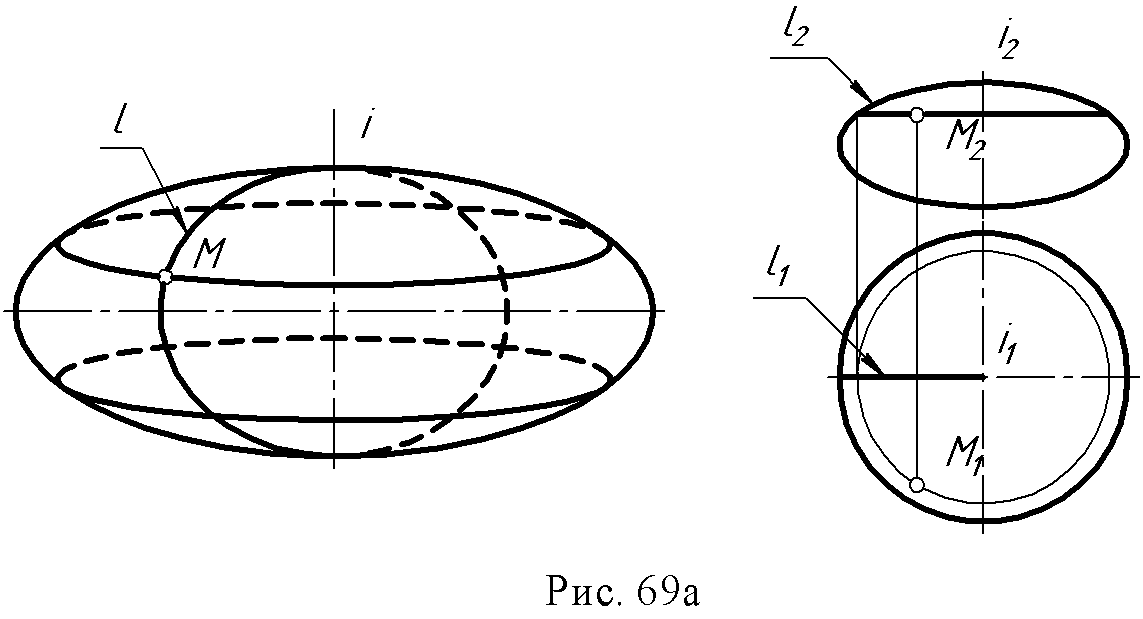 2. Параболоид вращения 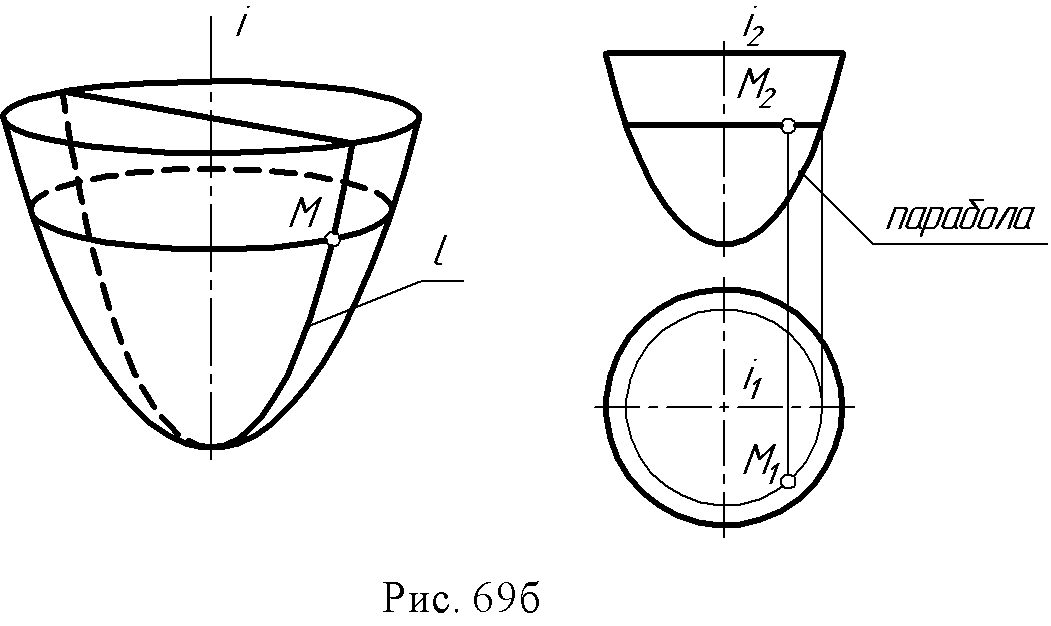 3. Гиперболоид вращения однополостный – образуется вращением гиперболы вокруг её мнимой оси: 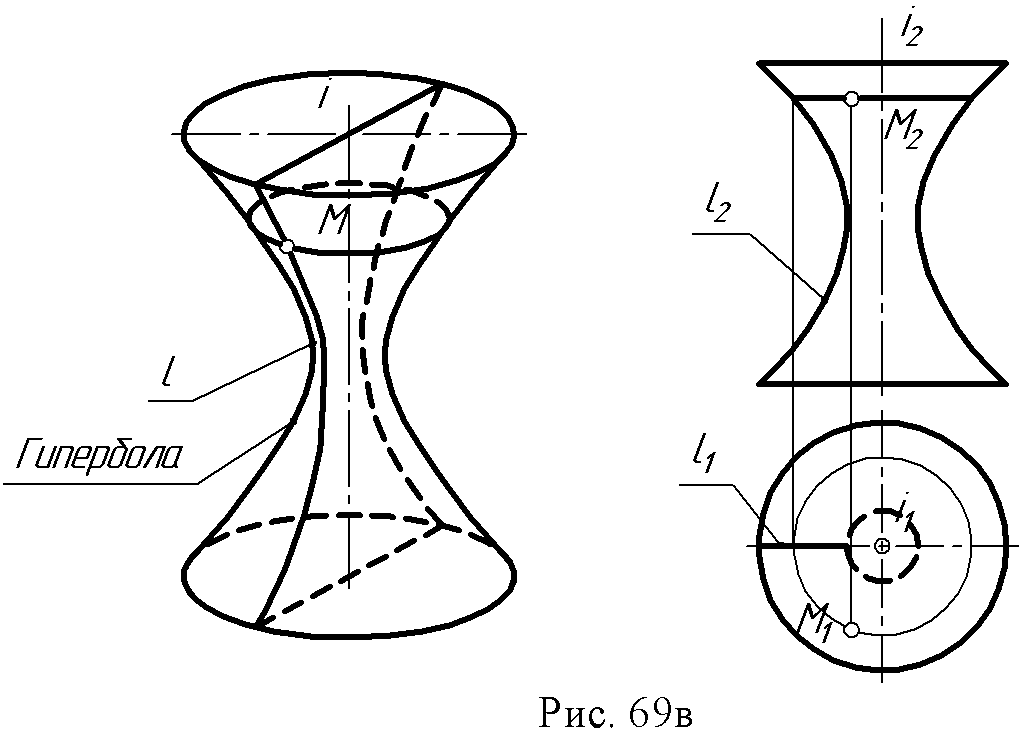 4. Гиперболоид вращения двуполостной - образуется вращением гиперболы вокруг действительной оси: 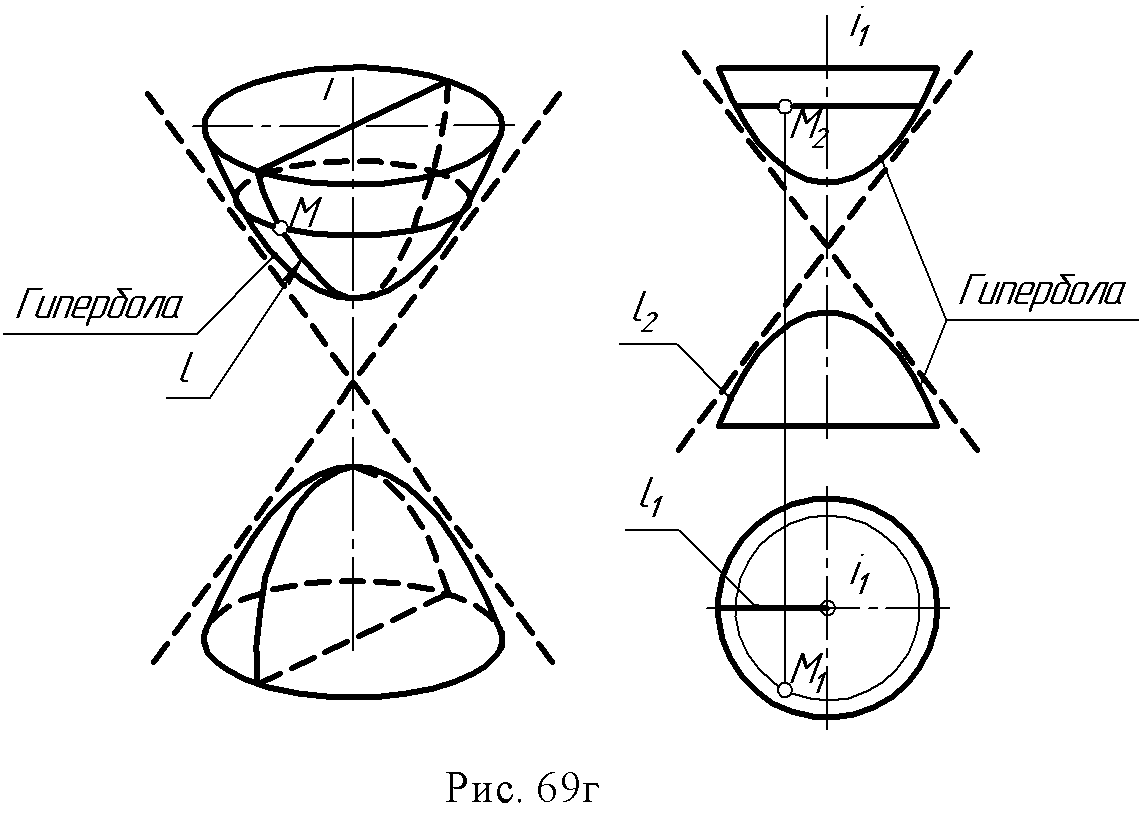 8.3. Принадлежность точки или линии поверхности. Для любой поверхности, если она задана, можно решить задачу на принадлежность точки или линии данной поверхности. Точка принадлежит поверхности, если она лежит на линии, принадлежащей данной поверхности (рис. 70 а, б). Для построения недостающей проекции точки на поверхности вращения через эту точку проводят параллель, для линейчатой поверхности – прямолинейную образующую. Например: 1. На поверхности тора определить горизонтальную проекцию точки А по заданной ее фронтальной проекции. Через точку А2проведена параллель k и на ней, используя линию проекционной связи, найдена точка А1. На этом чертеже показана плоскость главного меридиана. Это - сечение поверхности плоскостью α ||П2, проходящей через ось тора. 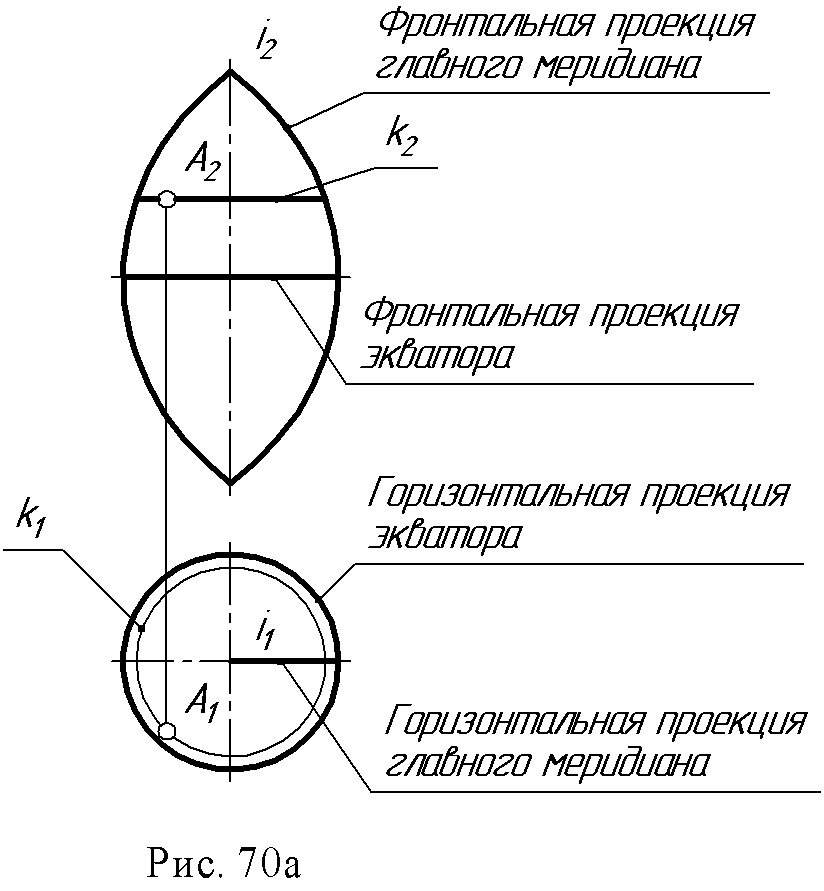 2. На поверхности конуса определить фронтальную проекцию точки В по заданной горизонтальной (рис. 70б). Через горизонтальную проекцию В1 проведена проекция образующей l1, построена фронтальная проекция образующей l2, и на ней лежит недостающая фронтальная проекция В2точки В. 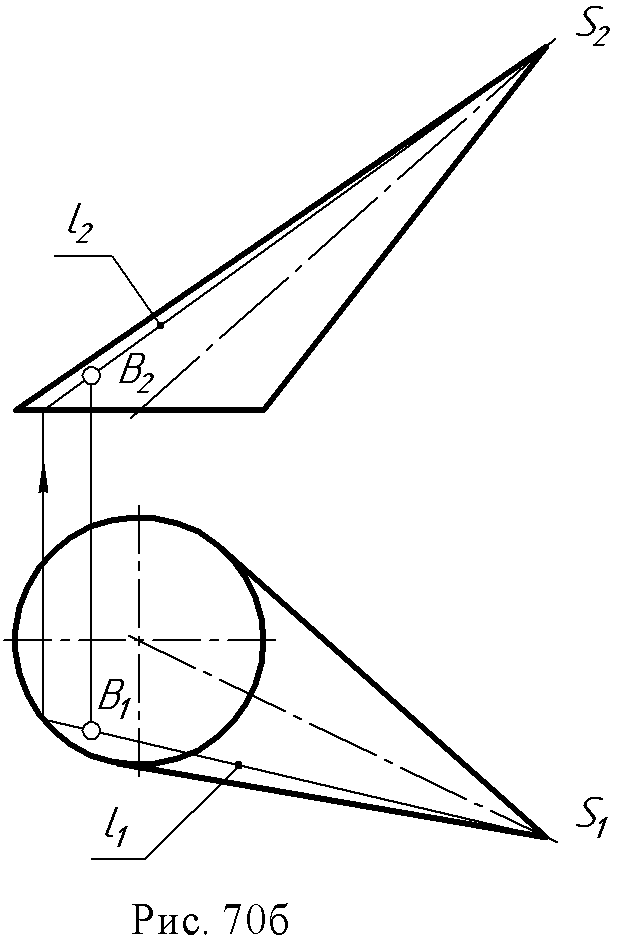 8.4. Вопросы для самопроверки
9. Лекция 9. Пересечение поверхности плоскостью. 9.1. Общие положення В результате пересечения кривой поверхности плоскостью в общем случае может получиться плоская кривая линия, характер которой зависит от вида поверхности и от положения плоскости. Полученная кривая линия складывается из точек, одновременно принадлежащих плоскости и поверхности. Пусть задана поверхность произвольного вида Ф и плоскость φ (рис.71). 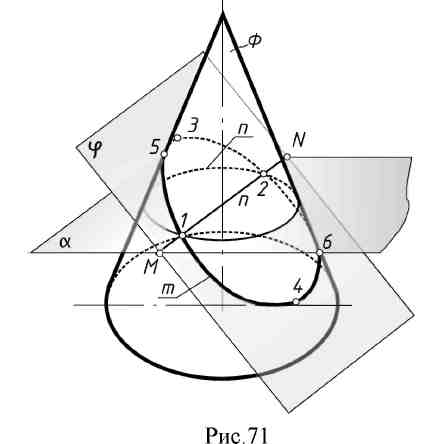 Алгоритм решения. 1. Поверхность и плоскость пересекают вспомогательной плоскостью посредником α. 2.Находят линию пересечения плоскости - посредника α с поверхностью Ф: n = Ф ∩ α 3. Находят линию пересечения плоскости - посредника с заданной плоскостью φ: MN= φ ∩ α. 4. Отмечают точки, в которых эти линии пересекутся: 1, 2 = (MN ∩ n). Точки 1 и 2, являясь общими для данных поверхности и плоскости, будут точками искомой линии пересечения.
9.2. Пересечение поверхности вращения плоскостью. Рассмотрим примеры построения линии пересечения поверхностей вращения плоскостью. При построении сечений следует выделить частный случай, когда секущая плоскость является проецирующей или пересекаемая поверхность занимает проецирующее положение. Пример 1. Построить пересечение конуса проецирующей плоскостью α(рис. 72а). Секущая плоскость является фронтально – проецирующей, поэтому фронтальная проекция линии пересечения лежит на следе плоскости (α2) и полученный в сечении эллипс проецируется на плоскость П2отрезком прямой 12 – 22. Горизонтальная проекция точек эллипса строится с помощью параллелей конуса. 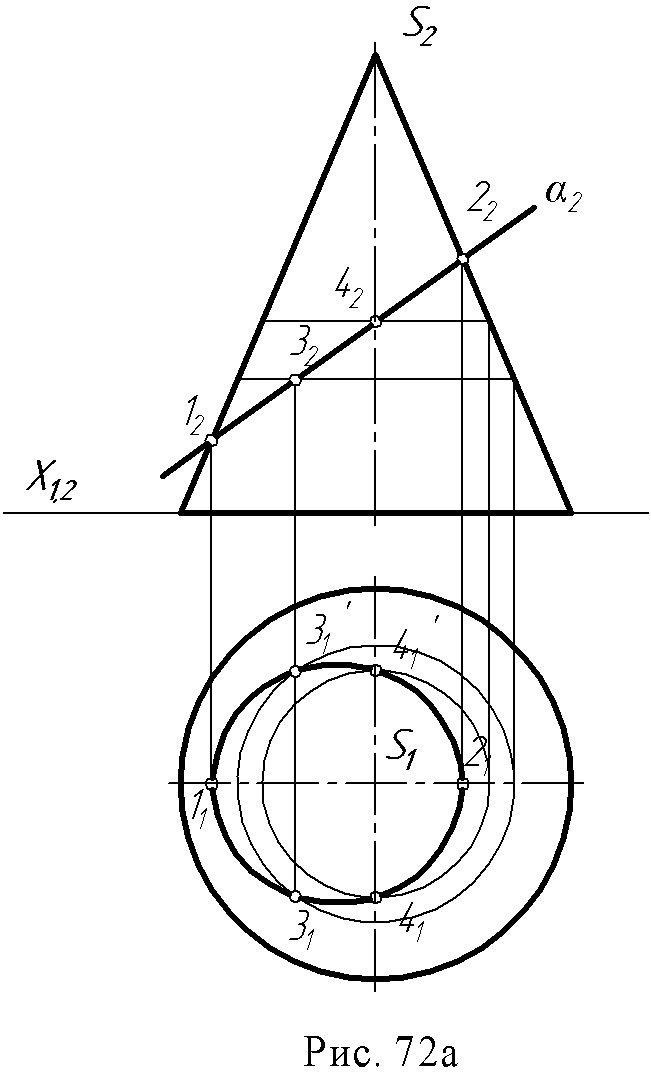 Пример 2. Построить линию пересечения конуса плоскостью общего положения (рис. 72б). Эта задача сложнее предыдущей, так как здесь отсутствуют проецирующие элементы, поэтому необходимо построить обе проекции линии сечения. Решение этой задачи может быть выполнено двумя способами. Первый способ (рис. 72б) – рассекаем поверхность и плоскость плоскостями посредниками частного положения, применяя изложенный выше алгоритм. 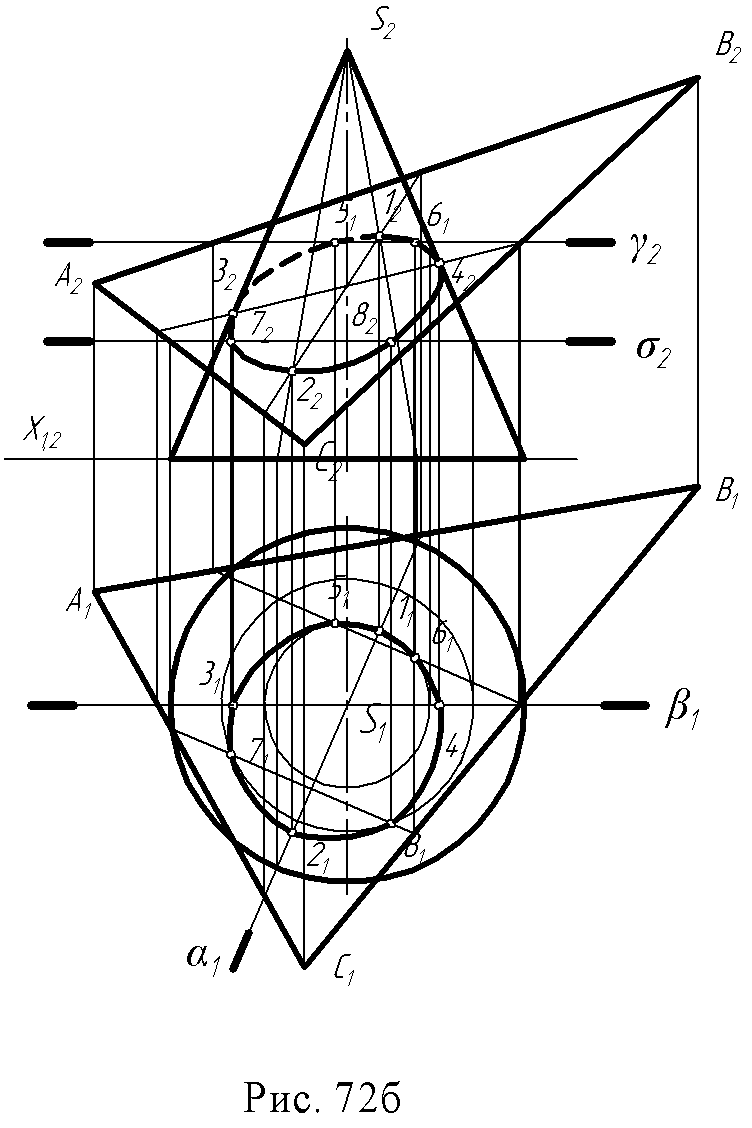 Сначала необходимо определить характерные (опорные) точки сечения: 1. Точки высшую и низшую (1 и 2), лежащие на оси симметрии сечения, определяют, рассекая плоскость и поверхность плоскостью α (α1), проходящей через линию ската (линию наибольшего наклона) заданной плоскости и через ось конуса; 2. Точки видимости, лежащие на очерковых образующих и разделяющие видимую и невидимую часть линии сечения – это точки 3 и 4, полученные с помощью секущей плоскости β (β1), проходящей параллельно плоскости П2 и через ось конуса; 3.Промежуточные точки – 5, 6, 7, 8 – которые получаются при рассечении поверхности и данной плоскости горизонтальными плоскостями - посредниками γ (γ2), σ (σ2). Через построенные проекции точек линии сечения проводится плавная кривая – эллипс. Рассмотренный пример дает представление об общем методе построения линии пересечения поверхности плоскостью. Второй способ (рис. 72в). 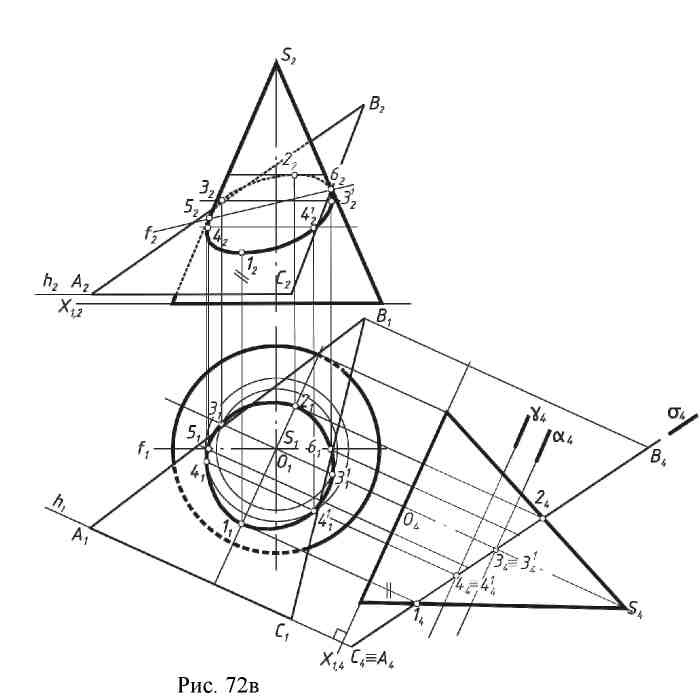 Он заключается в преобразовании чертежа замененной фронтальной плоскости проекций, при котором заданная плоскость общего положения преобразуется во фронтально - проецирующую. Новая ось Х1,,4и плоскость П4проводится перпендикулярно горизонтальной проекции горизонтали заданной плоскости (Х1,4 h1). Высшая и низшая точки 14и 24определяются на пересечении плоскости, вырожденной в линию σ4с новым очерком конуса. Часто заранее известен вид кривой, получающейся в сечении поверхности плоскостью. Так, сфера пересекается плоскостью всегда по окружности, цилиндр вращения пересекается плоскостью, в общем случае по эллипсу. Если же секущая плоскость параллельна или перпендикулярна оси цилиндра, то в сечении получается соответственно две образующие или окружность (рис. 73а). 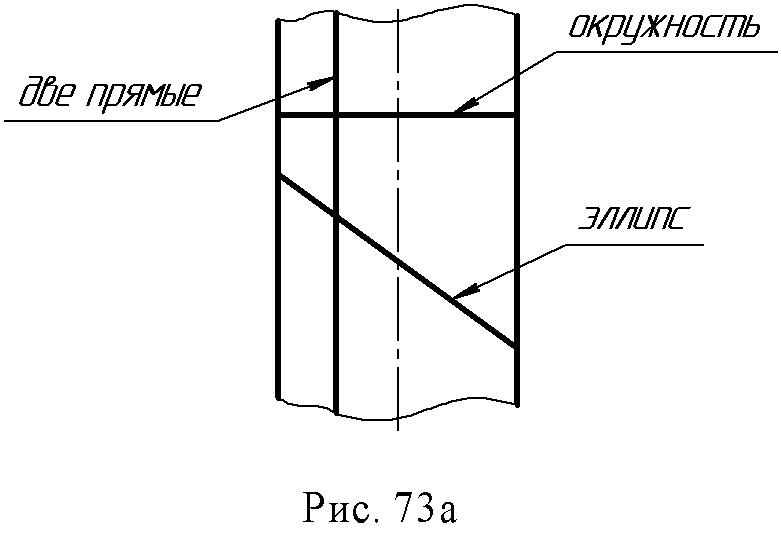 В сечении конуса вращения получаются все виды кривых второго порядка (конические сечения). Если секущая плоскость не параллельна ни одной из образующих конуса, т.е. пересекает все образующие, то в сечении получается эллипс. Если секущая плоскость перпендикулярна оси конуса, то получится окружность. Если секущая плоскость параллельна одной образующей конуса, то в сечении получается парабола. Если секущая плоскость параллельна двум образующим, то в сечении получается гипербола. В частности, если плоскость проходит через вершину конуса, в сечении получаются две образующие (рис. 73б). 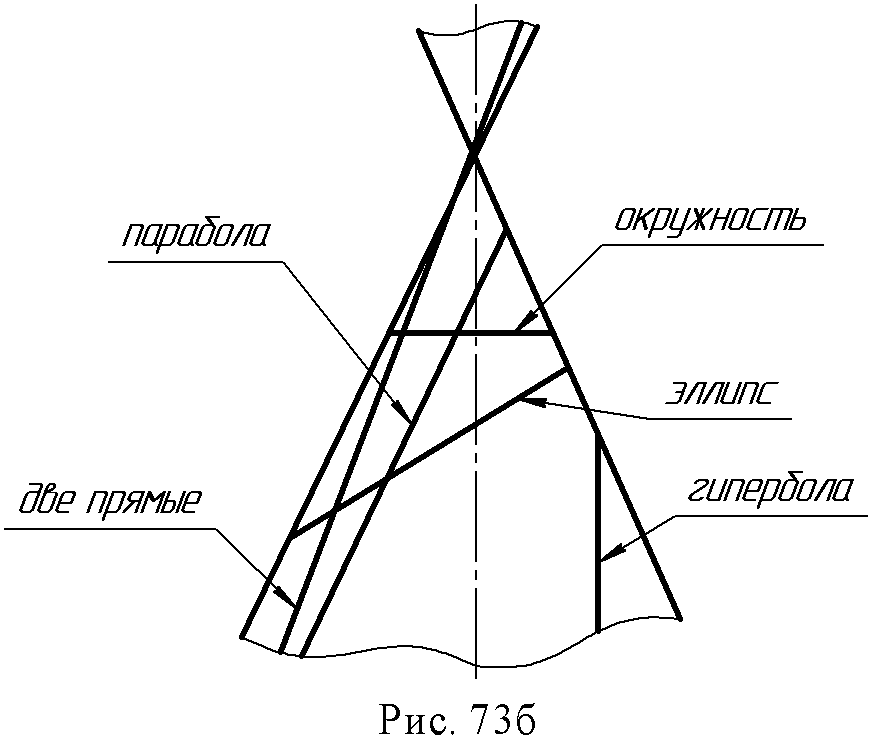 9.3. Пересечение гранной поверхности с плоскостью. Результатом пересечения гранной поверхности плоскостью является плоская ломаная линия; вершины этой ломаной можно определить как пересечение данной плоскости с ребрами гранной поверхности. Пример: Определить линию пересечения пирамиды SАВС с плоскостью ∆DEF (рис. 74). Находят точки пересечения ребер пирамиды с плоскостью. Например, через ребро SА (S1A1) проведена горизонтально - проецирующая плоскость α (α1), которая пересечет плоскость ∆DEF по линии 1-2 (11 - 21 12 - 22) на фронтальной проекции отмечена точка М (М2) - как пересечение S2A2 с линией (12 - 22); проекция М1 лежит на проекции S1A1. Такие построения выполнены с каждым ребром пирамиды. Получены точки К (К1 К2) и N (N1 ,N2). Соединив их, следует определить видимость. 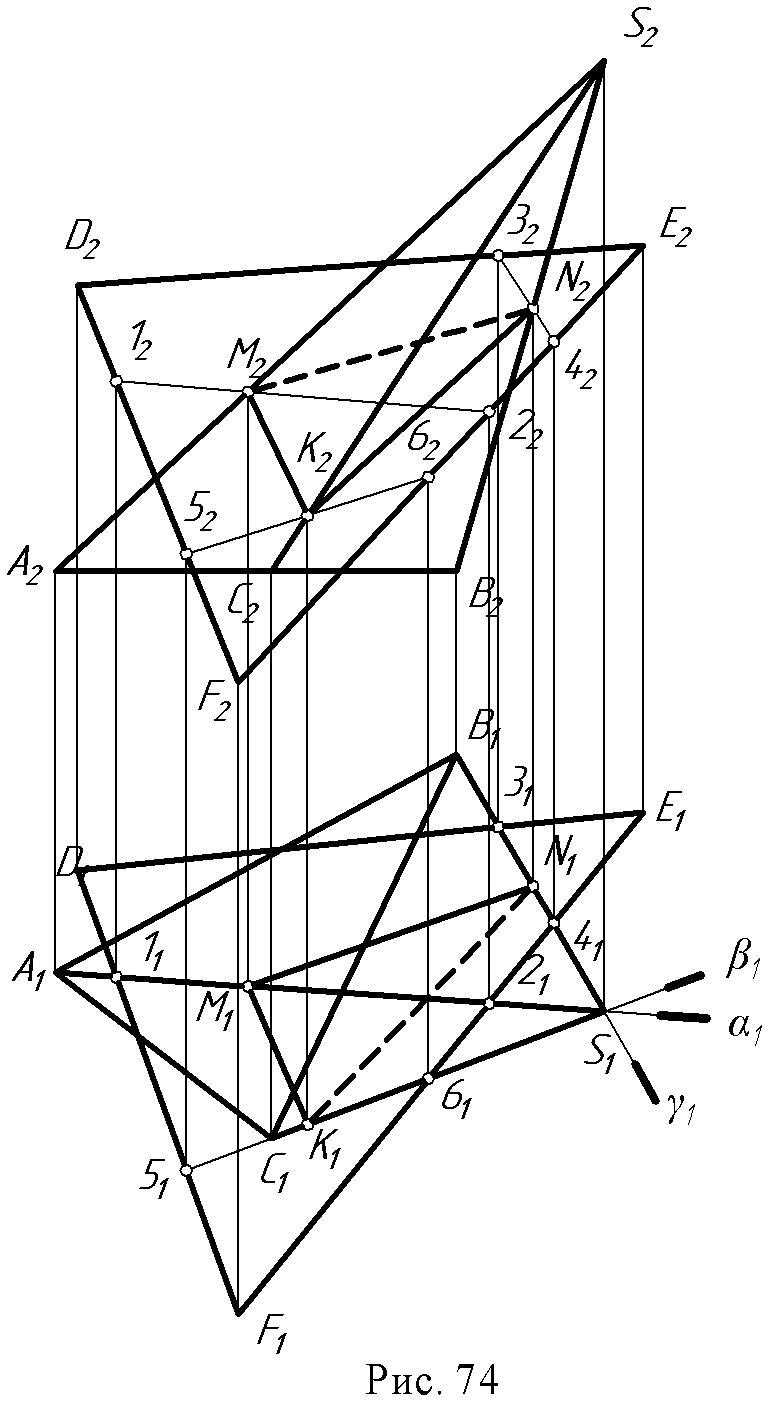 9.4. Вопросы для самопроверки
10.1. Общие положения Прямая линия может пересекать поверхность в одной, двух и более точках, может касаться ее. Если прямая не имеет общих точек с поверхностью, это означает, что она не пересекает поверхность. Этапы решения этой задачи аналогичны описанному ранее алгоритму на определение точки пересечения прямой с плоскостью. Через прямую АВ проводят вспомогательную плоскость – посредник α (рис. 75а). Находят линию пересечения поверхности с плоскостью α– (к). Отмечают точки пересечения линии АВ с линией К, точки 1 и 2. Количество точек пересечения прямой с поверхностью определяет порядок последней. 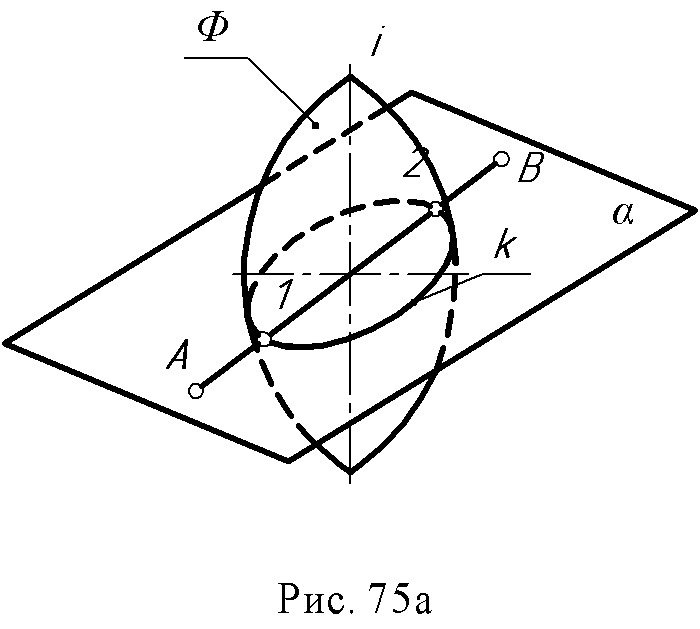 Решение задачи на комплексном чертеже (рис. 75б). Через прямую АВ проводят плоскость α П2; линию к строят, как это было описано выше. Отмечают точки пересечения линии к1 с А1В1 – точки 11 и 21 и находят их на фронтальной проекции. В качестве плоскости – посредника можно использовать и плоскость общего положения. Это применяют в том случае, когда заданная поверхность линейчатая, тогда при построении линии сечения вспомогательной плоскости – посредника с поверхностью избегают построения сечения как кривой линии. 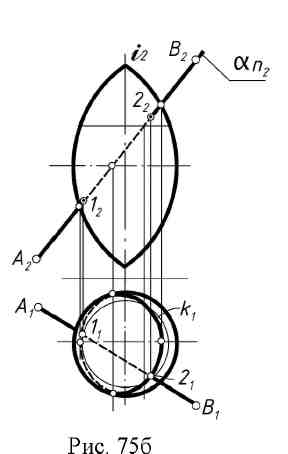 10.2. Примеры построения точек пересечения прямой с поверхностью Пример: Построить точки пересечения прямой АВ с конусом (рис. 76 а, б). Через прямую АВ проводят плоскость α общего положения, из условия, чтобы она пересекла конус по образующим. Следовательно, она должна пройти через вершину конуса. 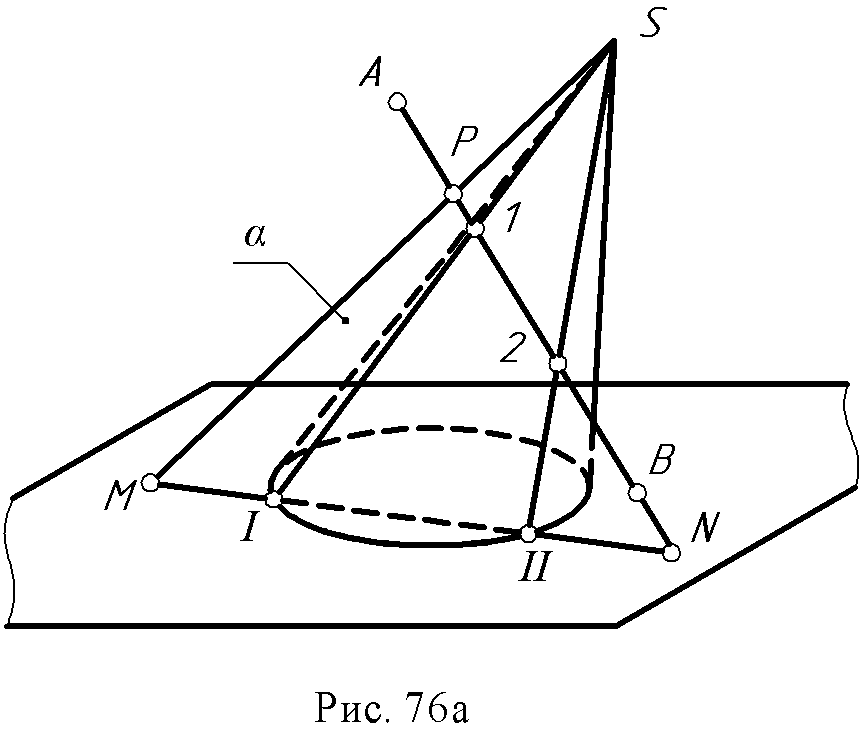 Введенная плоскость определяется пересекающимися прямыми АВ и РS, точка Р взята произвольно на АВ. Линия сечения плоскости с конусом - это образующие SI и SII, которые находят при помощи линии MN, являющейся линией пересечения (следом) плоскостей аи П1, т.е. с той плоскостью, в которой расположено основание конуса. Точки 1 и 2 - точки пересечения линии АВ с конусом - определяют как пересечение образующих SI и SII с прямой АВ. Решение задачи на комплексном чертеже (рис. 76б).
В случае, когда один из геометрических образов, участвующих в пересечении является проецирующим, задача сводится к задаче на принадлежность. 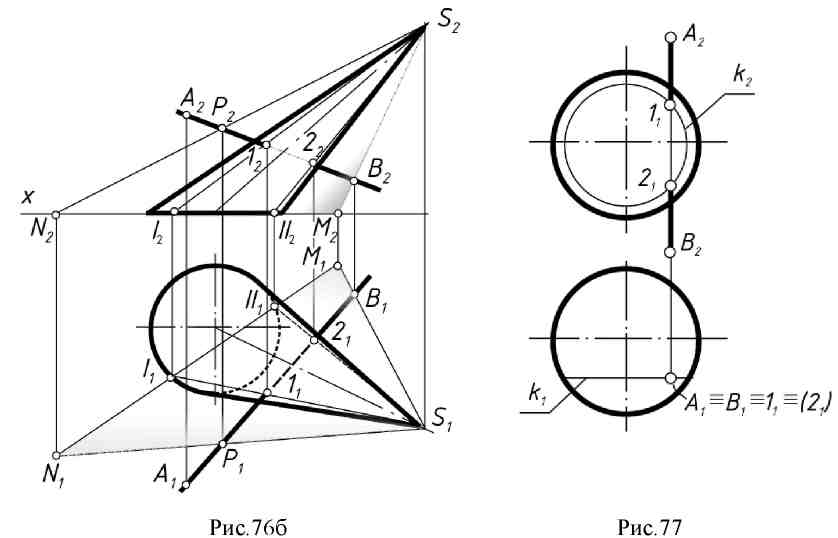 Пример: Определить точки пересечения прямой АВ со сферой (рис. 77). Прямая АВП1, следовательно, точки пересечения АВ со сферой на горизонтальной проекции совпадут с проекцией прямой - это точки 11и 21. Определить фронтальные их проекции можно с помощью окружности к. 10.3. Вопросы для самопроверки.
|
