39_tot (1)-конвертирован. Курс лекций по дисциплине теоретические основы теплотехники удк 621 016 Краткий курс лекций по дисциплине "Теоретические основы теплотехники" Учеб пособие А. А. Джамалуева, 2020. 127 с
 Скачать 0.66 Mb.
|
|
dq = du = Cv dT , (1.26) или для конечного изменения температуры и произвольной массы газа:  U = m Сv (T2 - T1). (1.27)Все тепло, которое подводится к газу в изохорном процессе, расходуется на увеличение внутренней энергии газа, т.е. газ нагревается. Изменение энтропии в изохорном процессе можно определить следующим образом: S2 – S1 = Cv ln (Р2/Р1) = Cv ln (T2/T1) . (1.28) Зависимость энтропии от температуры имеет логарифмический характер. Изобарный процесс Изобарным называют процесс, протекающий при постоянном давлении, p=const, dp=0. Связь между конечными и начальными параметрами выражается законом Гей – Люссака: в изобарном процессе объем газа прямо пропорционален его абсолютной температуре:
Количество теплоты, затраченное на расширение газа при постоянном давлении, равно изменению энтальпии газа:  q = = Сp (T2 - T1). (1.31)Изменение энтропии можно определить, зная изменение температур или объемов рабочего тела: S2 – S1 = Cр ln (v2/v1) = Cp ln (T2/T1) . (1.32) 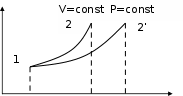 ТРисунок 1.3 – ТS - диаграмма изобарного и изохорного процессов Сравним на TS -диаграмме два процесса (рис.1.3) – изохорный (линия 1-2) и изобарный (линия 1-2’). Из рис.1.3 видно, что при нагревании газа до одной и той же температуры при постоянном давлении требуется затратить больше тепла , чем при постоянном объеме. Изотермический процесс Изотермическим называют процесс, протекающий при постоянной температуре, Т=const, dT=0. Связь между конечными и начальными параметрами выражается законом Бойля-Мариотта: при изотермическом сжатии давление газа возрастает, а при расширении –падает: Р2 / Р1 = V1 /V2 или РV = const . (1.33) Изменение внутренней энергии равно нулю, т.к. Т= const. В изотермическом процессе все тепло, подводимое к газу, расходуется на выполнение полезной работы. Работа изотермического процесса определяется : l = p1 v1 ln (v2 / v1) = R T ln (v2 / v1). (1.34) Изменение энтропии можно определить по формуле S2 – S1 = R ln (v2/v1) = R ln (P1/P2) . (1.35) Адиабатный процесс Адиабатным называют процесс, происходящий без теплообмена с окружающей средой, q=const, dq=0. Для осуществления такого процесса следует либо теплоизолировать газ, либо провести процесс настолько быстро, чтобы изменение температуры газа, обусловленное теплообменом, было пренебрежительно мало по сравнению с изменением температуры, вызванным расширением или сжатием газа. Уравнение адиабаты имеет следующий вид: р vк = const или p1v1к = p2 v2к, (1.36) где к - показатель адиабаты, зависящий от природы газа. 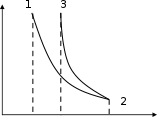 Сравним изотермический и адиабатный процессы на PV- диаграмме (рис. 1.4). Графиком изотермического процесса в pv- координатах, как показывает уравнение (1.33), является равнобокая гипербола, для которой оси служат асимптотами. Поскольку к >1, то линия адиабаты (2-3) идет круче линии изотермы (2-1).Р Рисунок 1.4 – РV-диаграмма изотермического и адиабатного процессов Для определения связи между основными параметрами адиабатного процесса решим совместно уравнение Клапейрона и уравнение адиабаты для 2 состояний. В результате получим:  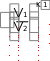 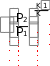 T2 .T1 Работа расширения при адиабатном процессе согласно 1-му закону термодинамики совершается за счет уменьшения внутренней энергии:   q = + l = 0 ; l = - u = Cv (T1 - T2). (1.37)Работу расширения в адиабатном процессе можно вычислить и по другой формуле: l = R (T1 – T2) / (к- 1) = (p1 v1 – p2v2) / (к -1). (1.38) Энтропия рабочего тела в адиабатном процессе не изменяется, т.к. dq=0. Следовательно, на TS-диаграмме адиабатный процесс изображается вертикальной линией. Политропные процессы Имеется группа процессов, которые протекают при постоянной теплоемкости. Условились эти процессы называть политропными. Они описываются уравнением вида р vn = const , где n –показатель политропы, может принимать любое численное значение в пределах от - ∞ до + ∞, но для данного процесса эта величина постоянная. Учитывая внешнее сходство уравнений политропы и адиабаты, можно связь между основными параметрами представить в следующем виде: 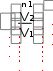 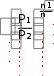 T1 T2 . Работа расширения в политропном процессе определяется по формуле l = R (T1 – T2) / (n- 1) = (p1 v1 – p2v2) / (n -1). (1.39) Количество подведенного (или отведенного) тепла можно определить с помощью 1-го закона термодинамики: q = Cv (n - к) (T2 –T1) / (n -1) = Cn (T2 – T1), где Cn- теплоемкость идеального газа в политропном процессе. Изменение энтропии в политропном процессе: S2 – S1 = Сn ln (T2 / T1). Политропный процесс имеет обобщающие значения, т.к. охватывает всю совокупность основных термодинамических процессов. Рассмотрим это на диаграммах рис.1.5. 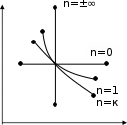 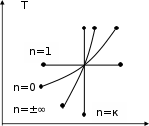 PV S Рисунок 1.5 – Частные случаи политропного процесса Из рис. 1.5 видно: для изобарного процесса - n=0, Сn = Cp; для изотермического процесса - n=1, Сn = ∞; для адиабатного процесса - n = к, Cn = 0; для изохорного процесса - n = ±∞, Cn=Cv. Процессы, находящиеся правее изохоры, характеризуются положительной работой, процессы, расположенные левее изохоры – отрицательной работой. Процессы, расположенные правее и выше адиабаты, идут с подводом теплоты к рабочему телу, процессы, лежащие левее и ниже адиабаты, протекают с отводом теплоты. Для процессов, расположенных над изотермой,характерно увеличение внутренней энергии; процессы, расположенные под изотермой, сопровождаются уменьшением внутренней энергии. Вопросы для самоконтроля Охарактеризуйте равновесные и неравновесные, обратимые и необратимые термодинамические процессы. Каким образом можно определить работу расширения? Какими свойствами обладает PV-диаграмма? Что характеризует внутренняя энергия рабочего тела и как ее можно рассчитать? В чем заключается сущность 1-го закона термодинамики? В чем заключается особенность 1-го закона термодинамики применительно к потоку газа? Что характеризует энтропия рабочего тела и каким образом ее можно определить? Свойства TS-диаграммы. Какие этапы включает в себя исследование термодинамических процессов идеальных газов? Дать характеристику изохорных процессов. Какова особенность изобарных процессов? Сравните эти процессы на TS-диаграмме. Охарактеризуйте изотермические процессы. Какова особенность адиабатных процессов? Сравните изотермический и адиабатный процесс на p-v-диаграмме. Покажите на диаграммах обобщающее значение поли- тропного процесса. Реальные газы Свойства реальных газов Реальные газы отличаются от идеальных тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой силами взаимодействия, имеющими электромагнитную и квантовую природу. Отличие свойств реальных газов от идеальных исключило возможность применения к ним в чистом виде законов идеального газа. При практических расчетах различных свойств реальных газов находит широкое применение отношение (1.40), которое получило название коэффициента сжимаемости (с): с = рv / R T. (1.40) Коэффициент сжимаемости характеризует отклонение свойств реального газа от свойств идеального. Для идеальных газов при любых условиях с=1, для реальных газов значение коэффициента сжимаемости в зависимости от давления и температуры может быть больше или меньше 1 и только при очень малых давлениях и высоких температурах оно практически равно единице. Одной из первых попыток аналитически описать свойства реальных газов является уравнение Ван-дер-Ваальса (1873 г.). Им было введено две поправки в уравнение Клапейрона:   a (v b) RTv2 , где a и b - постоянные для данного газа.   Слагаемое а / v2 в первом множителе учитывает влияние сил взаимодействия молекул; во втором множителе b учитывает влияние объема молекул. Легко видеть, что применительно к идеальному газу это уравнение принимает вид уравнения состояния Клапейрона. Практически пользоваться уравнением Ван-дер- Ваальса нельзя, т.к. оно дает результаты, недостаточно точные для нужд современной техники. Наиболее точным является в настоящее время уравнение состояния реальных газов, разработанное М.П.Вукаловичем и Н.И.Новиковым (1939 г.) При выводе своего уравнения авторы учитывали влияние ассоциации и диссоциации молекул под влиянием межмолекулярных сил взаимодействия: (P )(v b)RT 1 , где a,b - постояные уравнения Ван-дер-Ваальса, приведенные в справочных таблицах; c,m - коэффициенты, зависящие от природы газа, определяются экспериментально и приводятся в справочных таблицах. Однако для практических целей пользоваться этим, как и другими уравнениями состояния реального газа, неудобно вследствие сложности их и необходимости выполнения трудоемких вычислений. Обычно пользуются готовыми данными, например для водяного пара существуют таблицы водяного пара и энтальпийно- энтропийные диаграммы водяного пара. Во многих отраслях народного хозяйства в качестве рабочих тел используются пары различных веществ (воды, аммиака, углекислого газа, фреонов и др.) и атмосферный воздух. Наиболее часто используемые - это водяной пар и атмосферный воздух. Водяной пар Процесс превращения вещества из жидкого состояния в газообразное называют парообразованием. Испарением называют парообразование, которое происходит всегда при любой температуре со свободной поверхности жидкости или твердого тела. Сущность процесса испарения: отдельные молекулы, имеющие большие скорости, преодолевают притяжение соседних молекул и вылетают в окружающее пространство. Интенсивность испарения возрастает с увеличением температуры. Процесс кипения заключается в том, что если к жидкости подводить теплоту, то при некоторой температуре, зависящей от физических свойств рабочего тела и давления, наступает процесс парообразования как на свободной поверхности жидкости, так и внутри. Переход вещества из газообразного состояния в жидкое называется конденсацией. Процесс конденсации, так же как и процесс парообразования, протекает при постоянной температуре, если при этом давление не меняется. Если воду поместить в закрытый сосуд, то молекулы, испаряющиеся со свободной поверхности, будут заполнять пространство над жидкостью. Одновременно часть молекул будет снова возвращаться в жидкость. В некоторый момент количество молекул, вылетающих из жидкости, будет равно количеству молекул, возвращающихся в жидкость. В этот момент в пространстве над жидкостью будет находиться максимально возможное количество молекул. Пар в этом состоянии имеет максимальную плотность при данной температуре и называется насыщенным водяным паром, т.е. паром, соприкасающимся с жидкостью и находящимся в термическом с ней равновесии. С изменением температуры жидкости равновесие нарушается, вызывая соответствующее изменение плотности и давления насыщенного пара. Насыщенный пар, в котором отсутствуют взвешенные высокодисперсные частицы жидкой фазы, называется сухим насыщенным паром. Состояние сухого насыщенного пара определяется только одним параметром - давлением, или удельным объемом, или температурой. Насыщенный пар, в котором содержатся взвешенные высокодисперсные частицы жидкой фазы, равномерно распределенные по всей массе пара, называется влажным насыщенным паром. Отношение массы сухого насыщенного пара к суммарной массе влажного насыщенного пара называется степенью сухости пара или паросодержанием (х): для кипящей жидкости - х = 0; для сухого насыщенного пара - х = 1; для влажного насыщенного пара - 0 < x < 1. Массовая доля кипящей жидкости во влажном паре, равная (1- х), называется степенью влажности пара. Состояние влажного пара определяется двумя параметрами: температурой (или давлением) и степенью сухости пара. Если сухому насыщенному пару сообщить некоторое количество теплоты при постоянном давлении, то температура его будет возрастать. Такой пар называют перегретым, он при данном давлении имеет более высокую температуру и удельный объем, чем сухой насыщенный пар. Теперь, вспомнив основные понятия, можно приступить к рассмотрению PV– диаграммы процесса парообразования. Фазовая PV- диаграмма системы, состоящей из жидкости и пара, представляет собой график зависимости удельных объемов воды и пара от давления ( рис. 1.6). 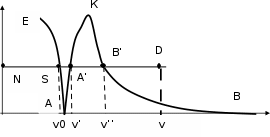 Р, ПаP А Рисунок 1.6 – PV-диаграмма водяного пара Пусть вода при 0оС и некотором давлении Р занимает удельный объем v0 (отрезок NS). Вся кривая АЕ выражает зависимость удельного объема воды от давления при температуре 00С. Кривая АЕ практически параллельна оси ординат, т.к. вода - вещество практически несжимаемое. Если при P=const сообщать воде теплоту, то ее температура и удельный объем будут расти. При некоторой температуре tн вода закипает, а ее удельный объем v` в точке A’ достигнет при данном давлении максимального значения. Кривая АК - зависимость удельного объема кипящей воды от давления, ее называют пограничной кривой жидкости (нижняя пограничная кривая). Характеристикой кривой АК является степень сухости х=0. При дальнейшем подводе теплоты при P=const начнется процесс парообразования. При этом количество воды уменьшается, а количество пара растет. В момент окончания парообразования в точке В’ пар будет сухим насыщенным. Если процесс парообразования протекает при P=const, то температура его не изменяется и процесс А’В’ является одновременно изобарным и изотермическим. Кривая КВ выражает зависимость удельного объема сухого насыщенного пара от давления, называется пограничной кривой газа (верхняя пограничная кривая). Характеристикой кривой КВ является степень сухости х=1. Точка А соответствует состоянию кипящей жидкости в тройной точке (t0=0.01о C), а изобара АВ соответствует состояниям равновесия всех трех фаз, она практически сливается с осью абсцисс (Р0=0.00611 бар). Если к сухому насыщенному пару подводить теплоту при P=const, то его температура и объем будут расти, а пар из сухого насыщенного перейдет в перегретый (точка D). На диаграмме можно выделить следующие характерные зоны: между осью ординат и изотермой ЕА - "вода + лед"; между ЕА и нижней пограничной кривой АК - "жидкость"; между нижней и верхней пограничными кривыми АК и КВ - "вода + пар"; вправо и вверх от КВ - "перегретый пар". Точку А (вода находится одновременно в жидком, твердом и газообразном состояниях) называют тройной точкой воды, ее параметры: Р0 = 0.00611 бар, Т = 0.01о C, V0 = 0.001 м3 / кг. Верхняя и нижняя пограничные кривые сходятся в одной точке К, которую называют критической точкой. Критическая точка является конечной точкой фазового перехода «жидкость – пар», начинающегося в тройной точке воды. Выше этой точки существование вещества в двухфазном состоянии невозможно. Параметры критической точки для воды: Tк = 374.12о С; vк = 0.00314 м3/кг; pк = 22.15 МПа. Для практических расчетов теплоэнергетических процессов, в которых используется водяной пар, требуются термодинамические параметры кипящей воды и сухого насыщенного пара. Эти данные берут из таблиц теплофизических свойств воды и водяного пара, которые получены расчетами по уравнению Вукаловича- Новикова. В этих таблицах величины со штрихом относятся к воде, нагретой до температуры кипения, а величины с двумя штрихами - к сухому насыщенному пару. За нулевое состояние, от которого отсчитываются величины энтальпии и энтропии, условно принято состояние воды в тройной точке. Количество теплоты, затраченное на парообразование 1кг воды при температуре кипения до сухого насыщенного пара, называется удельной теплотой парообразования и обозначается - r, кДж/кг. Состояние кипящей воды и сухого насыщенного пара определяется только одним параметром, поэтому по известному давлению или температуре по таблице можно определить все эти значения. Удельная внутренняя энергия определяется из общей формулы для энтальпии: |