39_tot (1)-конвертирован. Курс лекций по дисциплине теоретические основы теплотехники удк 621 016 Краткий курс лекций по дисциплине "Теоретические основы теплотехники" Учеб пособие А. А. Джамалуева, 2020. 127 с
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
l p*dv v1В общем случае, когда масса газа не равна 1 кг, полная работа (L), совершаемая системой, определяется по формуле L = l m . Работу, совершаемую системой над окружающей средой, (расширение) принято считать положительной (полезной), а работу, совершаемую окружающей средой над системой, (сжатие) - отрицательной. Единицами измерения полной работы в системе СИ является джоуль (Дж), удельной работы – Дж / кг. Работа всегда связана с перемещением тел в пространстве, поэтому она характеризует упорядоченную форму передачи энергии от одного тела к другому и является мерой переданной энергии. Поскольку величина работы пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую, целесообразно выбирать такие, которые допускают значительные увеличения объема. Этим качеством обладают газы и пары жидкостей. Внутренняя энергия газа Внутренняя энергия системы включает в себя: кинетическую энергию поступательного, вращательного и колебательного движения частиц; потенциальную энергию взаимодействия частиц; энергию электронных оболочек атомов; внутриядерную энергию. В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в дальнейшем под внутренней энергией мы будем понимать энергию хаотического движения молекул и атомов, а также потенциальную энергию сил взаимодействия между молекулами. Кинетическая энергия молекул является однозначной функцией температуры, значение потенциальной энергии зависит от среднего расстояния между молекулами, следовательно, от занимаемого газом объема. Внутренняя энергия зависит только от основных параметров газа, поэтому является 4-м параметром состояния газа. Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодействия между молекулами, не зависит от объема газа или давления, а определяется только его температурой. Обозначим полную внутреннюю энергию газа U (джоуль), а удельную, отнесенную к 1 кг газа, - u (джоуль на килограмм). В термодинамике определяют не абсолютное значение внутренней энергии, а ее изменение. Поэтому условно за нулевую точку отсчета произвольно взята температура Т = 273 К. ∆U = U2 – U1, где U1 – внутренняя энергия в начальном состоянии, Дж; U2 – внутренняя энергия в конечном состоянии, Дж. Для бесконечно малого изменения состояния: du =Cv dT. Изменение полной внутренней энергии для конечного интервала изменения температуры можно определить по формулам: ∆u = Сv(T2–T1); ∆U = m Сv (T2–T1). В этих формула Аналитическое выражение 1-го закона термодинамики. Энтальпия Первый закон термодинамики представляет собой частный случай всеобщего закона сохранения и превращения энергии применительно к тепловым процессам. Этот закон является фундаментальным законом природы, который получен на основе обобщения огромного количества экспериментальных данных и применим ко всем явлениям природы. Он утверждает, что энергия не исчезает и не возникает вновь, она лишь переходит из одной формы в другую, причем убыль энергии одного вида дает эквивалентное количество энергии другого вида. Рассмотрим некоторое рабочее тело (газ) с объемом V и массой m, имеющее температуру Т и давление Р. Газу сообщается извне определенное количество тепла Q. В результате подвода теплоты газ будет нагреваться и расширяться. С энергетической точки зрения повышение температуры тела свидетельствует о увеличении внутренней энергии. Поскольку рабочее тело окружено средой, которая оказывает на него давление, то при своем расширении оно производит полезную работу против его внешнего давления. Так как никаких других изменений в системе не происходит, то по закону сохранения энергии можно записать: dQ = dU + dL (1.12) или, если масса равна 1кг, - dq = du + dl = du + p dv, (1.13) т.е. теплота, сообщаемая системе, идет на приращение ее внутренней энергии и на совершение полезной работы. Полученное уравнение является математическим выражением первого закона термодинамики. Рассмотрим уравнение (1.13): работу запишем как произведение давления на изменение объема (dl=pdv) и, используя математический прием (прибавление и вычитание одной и той же величины vdp), проведем математические преобразования: dq=du+pdv+vdp-vdp=du+d(pv)-vdp=d(u+pv)-vdp. Обозначим величину u+pv буквой h (энтальпия) и получим: dq = dh – v dp. (1.14) Энтальпия представляет собой полную энергию термодинамической системы, равную сумме внутренней энергии системы и потенциальной энергии, которая обусловлена тем, что газ находится под давлением. Единицы измерения полной энтальпии (Н) - джоуль, удельной энтальпии (h) – джоуль на килограмм. Рассмотрим элементарное изменение энтальпии: dh = du + d(pv). Подставим в это уравнение dU=Cv dt и рv=RT: dh = Cv dt + R dt = dT (Cv + R) = Cp dT или для конечного процесса при произвольной массе газа:  H = m Сp (T2 - T1). (1.15) H = m Сp (T2 - T1). (1.15)Энтальпия – это теплота, подводимая к телу в процессе нагрева его при постоянном давлении. Энтальпия является функцией основных параметров (u,p,v) и принята за 5-й основной параметр состояния рабочего тела. Первый закон термодинамики для потока газа Рассмотрим схематичную работу теплового двигателя. Поток газа массой 1 кг с параметрами - давление р1, удельный объем v1 и  скорость - через входной патрубок поступает в тепловой скорость - через входной патрубок поступает в тепловойЗапишем 1-й закон термодинамики в общем виде:  q = + l. (1.16) q = + l. (1.16)Проанализируем каждый член уравнения (1.16). Теплота q состоит из 2 частей: теплоты, подводимой к потоку извне, qн и теплоты, возникающей за счет трения подвижных частей о неподвижные, qтр.  Изменение внутренней энергии определяется разностью Изменение внутренней энергии определяется разностьювнутренней энергии газа в конечном и начальном состоянии. Работа расширения газа состоит из 5 составных частей : работа по вталкиванию порций газа во входном патрубке - работа выполняется за счет внешнего источника энергии, считается отрицательной, эта работа вталкивания равна р1v1 ; работа, которую выполняет газ после агрегата по выталкиванию предыдущей порции газа из патрубка - эта работа положительная и равна р2v2 ; часть работы расходуется на трение – lтр ; полезная (техническая) работа, которая выполняется в агрегате – lт ; работа, которая расходуется на увеличение кинетической энергии потока газа. Подставим полученную информацию в уравнение (1.16) : qн+qтр= u2-u1 - p1v1 + p2v2 + lтр+ lт + (ω22 – ω12) / 2. В данном выражении qтр= lтр (согласно закону сохранения энергии), u2 + p2v2 = h2 и u1 + p1v1 = h1 , тогда qн = h2 - h1 + lт + (ω22 – ω12) / 2 . (1.17) Уравнение (1.17) является математическим выражением 1-го законa термодинамики для потока газа. В дифференциальном виде уравнение имеет вид  dqн = dh + dlт + d (1.18) dqн = dh + dlт + d (1.18)Количество теплоты, подводимое к потоку газа извне, расходуется на увеличение энтальпии потока газа, увеличение кинетической энергии и на выполнение технической работы. Энтропия газов Клаузиусом для более полного исследования термодинамических процессов был введен 6-й параметр состояния энтропия. Величина dq=du+pdv не является полным дифференциалом. Действительно, чтобы проинтегрировать правую часть, нужно знать зависимость давления от объема, т.е. процесс, который совершает газ. В математике есть прием превращения в полный дифференциал путем умножения ( или деления) на интегрирующий множитель (или делитель). Для элементарного количества теплоты dq интегрирующим делителем является абсолютная температура Т. Рассмотрим это на примере идеального газа. Подставим в уравнение (1.13) выражения для внутренней энергии,а давление выразим через параметры газа: dq = Cv dT + R T dv / v. (1.19) Для превращения в полный дифференциал разделим обе части уравнения (1.19) на абсолютную температуру Т: dq / T = Cv dT / T + R dv / v. (1.20) Величина dq /T при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния и называется энтропией (ds). Единицы измерения полной энтропии (S) – джоуль на кельвин, удельной энтропии (s) – джоуль на килограмм-кельвин . Энтропия – функция состояния термодинамической системы, которая характеризует хаотичность (неупорядоченность) системы. Энтропию часто называют приведенной теплотой, т.к. она показывает отношение теплоты до абсолютной температуры газа. После интегрирования уравнения (1.20) получим : S2 S1 C ln T2  v T1 R ln v2  v1 v1. (1.21) Используя уравнение Клапейрона, можно легко получить выражения изменения энтропии через другие параметры рабочего тела: 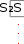 1 Cv 1 Cvln P2  P1 P1ln v2  C v1 C v1; (1.22) S2 S1 C ln T2  v T1 R ln v2  v1 v1. (1.23) Энтропия есть функция состояния рабочего тела, поэтому уравнениями (1.21) – (1.23) можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями. Понятие энтропии позволяет ввести удобную для термодинамических расчетов TS-диаграмму, на которой состояние системы изображается точкой, а равновесный процесс – линией (рис.1.2). Из определения энтропии можно записать: dq=TdS. (1.24) Из уравнения (2.12) видно, что тепло и энтропия изменяются в одном и том же направлении, т.к. абсолютная температура всегда положительна: при нагревании тела (dq>0) его энтропия возрастает (dS>0), при охлаждении тела (dq<0) его энтропия убывает (dS<0). 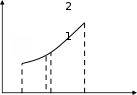 Т, К Т, КТ2 Т1 S1 dS S2 S, Дж/(кг К) Рисунок 1.2 – TS-диаграмма Выделим на TS-диаграмме элементарное изменение энтропии dS. Произведение TdS характеризует площадь прямоугольника и равно элементарной теплоте. Проинтегрируем уравнение (1.24). Геометрический смысл интеграла - это сумма элементарных площадей dST , т.е. получим площадь, ограниченную линиями S2=const, S1=const и линией процесса 1-2 (см. рис. 1.2):  S 2 S 2q TdS S1 . Таким образом, на TS-диаграмме площадь, ограниченная линий процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса. Термодинамические процессы идеальных газов 1-й закон термодинамики устанавливает связь между теплотой, изменением внутренней энергии и механической работой. При этом количество теплоты, подводимое к рабочему телу, зависит от способа подвода теплоты или характера термодинамического процесса. Выделяют следующие методы подвода теплоты к рабочему телу: изохорный - V = const; изобарный - P = const; изотермический - T = const; адиабатный - q = const; политропный - С = const. При исследовании термодинамических процессов необходимо: Построить процесс на PV- и TS-диаграммах. Определить начальные и конечные параметры рабочего тела. Вывести уравнение процесса, устанавливающее связь между начальными и конечными параметрами рабочего тела в данном процессе. Определить изменение внутренней энергии, энтропии и величину работы изменения объема газа. Рассмотрим по данной схеме основные термодинамические процессы. Изохорный процесс Изохорным называют процесс, протекающий при неизменном объеме рабочего тела, V=const , dV=0. Связь между конечными и начальными параметрами выражается законом Шарля: при постоянном объеме давление газа прямо пропорционально его абсолютной температуре: Р2 / Р1 = Т2 / Т1. (1.25) Работа расширения в изохорном процессе равна нулю, так как изменение объема равно нулю. Следовательно, согласно 1-му закону термодинамики можно записать: |
