39_tot (1)-конвертирован. Курс лекций по дисциплине теоретические основы теплотехники удк 621 016 Краткий курс лекций по дисциплине "Теоретические основы теплотехники" Учеб пособие А. А. Джамалуева, 2020. 127 с

• Название: Курс лекций по дисциплине теоретические основы теплотехники удк 621 016 Краткий курс лекций по дисциплине "Теоретические основы теплотехники" Учеб пособие А. А. Джамалуева, 2020. 127 с
• Дата: 28.12.2021
• Размер: 0.66 Mb.
• Имя файла: 39_tot (1)-конвертирован.docx
• Тип: Курс лекций; #320815
• страница: 6 из 11

const A _.

После вторичного интегрирования получаем: t = Ax + B.

При постоянной теплопроводности это уравнение прямой линии. Следовательно, закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.

Найдем постоянные интегрирования А и В.

При х=0 <sup>t

t</sup>ст

^В; при х = δ ^t

t_ст А

^tст

Тогда ^A

(t_ст t_ст) / _{.
dt t} // _t /

Таким образом мы нашли градиент температуры: A

dx

cm cm _.

δ

Согласно закону Фурье:
q = - grad t = -

dn dx

// /


t t
cm cm

δ

или q =
^λ (t^/ t ^// ) . (2.5)

_δ cт cт

Зная плотность теплового потока, можно вычислить общее количество теплоты, которое передается через поверхность стенки f за время

(2.6)


.
Полученное уравнение справедливо для случая, когда теплопроводность - постоянная величина. В действительности = f(t). В большинстве практических задач приближенно предполагается, что коэффициент не зависит от температуры и одинаков по всей толщине стенки. Значение находят в

cm
справочниках при температуре t = 0,5 (t^/

_t // ₎ cm

Отношение λ/δ называют тепловой проводимостью стенки, а обратную величину δ/λ - тепловым или внутренним термическим сопротивлением стенки и обозначают R_λ.

В тепловых аппаратах часто встречаются стенки, состоящие из нескольких плоских слоев различных материалов. Для получения уравнения для этого случая необходимо записать уравнение теплопроводности для каждого отдельного cлоя и учесть, что тепловой поток, проходящий через любую изотермическую поверхность, один и тот же. Рассмотрим для случая 3-слойной стенки (рис. 2.3).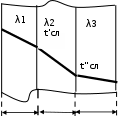

t’_ст
t’’_ст

δ₁ δ₂ δ₃

, - толщина слоев; ₁ , ₂ ,

- коэффициент

теплопроводности слоев; поверхностей стенки;

^tст <sup>,

t</sup>ст

• 
  температуры наружных
  

^tсл <sup>,

t</sup>сл

- температуры между слоями

Рисунок 2.3 – Теплопроводность многослойной плоской стенки


*
Запишем тепловой поток для каждого слоя:

ст
Q^* F(t

ст ^{) ; Q}*

F(t_сл

сл ^{) ; Q}

F(t_сл

ст ^{) .}

Решим эти уравнения относительно разности температуры:

^tст сл

^{; t}сл сл

; ^tсл ст .

Просуммируем эти три уравнения:

	1	2	3
F	1	2	3

^tст сл ^.
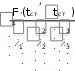Выразим из полученного уравнения тепловой поток:




_Q*

. (2.7)

Для любого числа слоев формула (2.7) имеет вид

Q
^{* F(t}ст^tст n

)

. (2.8)

i
^{i 1} i
Величину называют полным внутренним термическим
сопротивлением многослойной стенки. Распределение температур в пределах каждого слоя линейное, однако в различных слоях

крутизна температурной зависимости различна (крутизна больше в слоях с меньшей теплопроводностью).

Рассчитав тепловой поток через многослойную стенку, можно определить падение температуры в каждом слое и найти температуру на границе всех слоев.

6. 
   Теплопроводность через цилиндрическую стенку при стационарном режиме и
   

граничных условиях 1-го рода

Очень часто теплоносители движутся по трубам и требуется рассчитать тепловой поток, передаваемый через цилиндрическую стенку трубы. Эта задача также одномерная, если ее рассматривать в цилиндрических координатах (рис. 2.4). Температура изменяется только вдоль радиуса (по координате r), а по длине трубы и ее периметру остается неизменной. В этом случае grad t = dt / dr.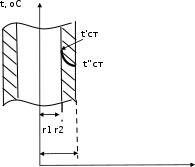





r, м

Рисунок 2.4 – Теплопроводность цилиндрической стенки

Запишем закон Фурье в общем виде (2.1) и подставим в него выражения для площади цилиндрической стенки (F = 2 π r l) и градиента температуры (qrad t = dt / dr):

Q^* (2

rl) ^dt _.

dr

Разделим переменные величины dt и dr и проинтегрируем обе части уравнения:

1
_; t ^Q ln^r2
. (2.9)

^tст

^ст2  r

Из уравнения (2.9) видно, что изменение температуры при прохождении теплоты через цилиндрическую стенку имеет логарифмический характер.

Умножим обе части уравнения (2.9) на (-1) и выразим тепловой поток:

_Q*




r₁

где d – диаметр трубы, м.

, (2.10)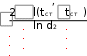


d₁

Внутреннее термическое сопротивление цилиндрической стенки рассчитывается по следующей формуле:

R ln ^{d 2} _.

d₁
Для многослойной цилиндрической стенки (например, теплоцентраль) уравнение для определения теплового потока будет иметь следующий вид:

_Q* _.

6. 
   Теплопроводность при стационарном режиме и граничных условиях 3-го рода
   

(теплопередача)

Граничные условия 3-го рода задаются температурами стенки и окружающей среды и условиями теплообмена - уравнение Ньютона

– Рихмана (2.4).

Процесс теплообмена между поверхностью твердого тела и жидкостью (газом) называют теплоотдачей.

Процесс переноса теплоты от одной подвижной среды (горячей) к другой (холодной) через разделяющую их стенку называется теплопередачей. Разделяющая стенка может служить проводником теплоты (в этом случае она изготавливается из материала с высоким коэффициентом теплопроводности ) и изолятором для уменьшения потерь теплоты (изготавливается из материала с хорошими изоляционными свойствами).

Теплопередача представляет собой сложный процесс.

Рассмотрим наиболее простые случаи.

1-й случай - теплопередача через плоскую стенку. Примером является передача теплоты из помещения в окружающую среду.

Рассмотрим однослойную плоскую стенку (рис. 2.5).

λ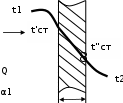










2
α₂
δ

Рисунок 2.5 – Теплопередача через плоскую стенку

Процесс теплопередачи осуществляется в 3 этапа:

теплоотдача от горячей среды (t₁) к стенке – уравнение Ньютона-Рихмана:


*
Q ₁F(t ) _,

где

- коэффициент теплоотдачи, Вт/(м² К); теплопроводность через плоскую стенку:

ст ст
Q^* F(t t ) _;
теплоотдача от внешней поверхности стенки к холодному теплоносителю – уравнение Ньютона-Рихмана:


*
Q ₂ F(t_ст t₂ ) _.

Величины тепловых потоков во всех 3 уравнениях одинаковы, т.к. процесс стационарный – сколько тепла стенка воспринимает, столько же и отдает. Выразим из каждого уравнения разность температур: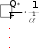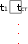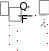
; ; .
Сложим левые и правые части и выразим тепловой поток:
^Q* . (2.11)

Обозначив

^k , получим:

Q Fk(t<sub>1

2</sub> ⁾ .

*
Соответственно, можно записать уравнение для плотности теплового потока:

q = к (t₁ – t₂). (2.12)

Полученное уравнение (2.12) называют уравнением теплопередачи. Рассмотрим физическую суть коэффициента теплопередачи, Вт/(м² К):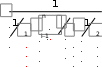

^k . (2.13)

Числовое значение коэффициента теплопередачи выражает количество теплоты, проходящей через единицу поверхности стенки в единицу времени от горячего к холодному теплоносителю при разности температур между ними в 1 ^оС.

Исходя из уравнения (2.13) можно предложить следующие

способы интенсификации теплопередачи:

повысить коэффициенты теплоотдачи;

уменьшить толщину стенки, разделяющей среды;

заменить материал стенки на более теплопроводный.

Величина, обратная коэффициенту теплопередачи называется общим термическим сопротивлением однослойной плоской стенк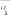и:

где ¹ и

R _,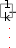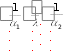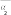
¹ - внешние термические сопротивления; -

внутреннее термическое сопротивление стенки.

Общее термическое сопротивление через многослойную плоскую стенку соответственно равно:

R _.
Рассмотрим 2-й случай теплопередачи - теплопередачу через цилиндрическую стенку. Процесс передачи тепла от горячей

^{воды, движущейся по цилиндрической трубе (с температурой} t₁ ^и

коэффициентом теплоотдачи ₁ ) к холодному теплоносителю (с

^{температурой} t₂

рис. 2.6.

и коэффициентом теплоотдачи ₂ ), изображен на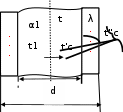

t

d₁ и d ₂

- внутренний и наружный диаметр трубы

Рисунок 2.6 – Теплопередача через цилиндрическую стенку Тепловой поток от воды к внутренней стенке равен:

Q ₁ d₁l(t₁ t_ст ) _.

Тепловой поток по стенке трубы

(t t ^* )

_Q^* ст ст _.

ln d ₂ / d₁

Тепловой поток от наружной стенки к воздуху

*
^{Q d2l(tст t2 )} .
Решим эти уравнения относительно разности температур, а затем сложим левые и правые части: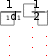

d 1

( ln² ) _.

Определим тепловой поток:

_Q*

^d1 2 ^d2


. (2.14)

Коэффициент теплопередачи для цилиндрической стенки или

линейный коэффициент теплопередачи, Вт/(м К):
K

ц ,

В общем случае для многослойной цилиндрической стенки, имеющей n слоев,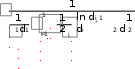

^Kц ^{. (2.15)}


Числовое значение линейного коэффициента теплопередачи (К_ц ) равно количеству теплоты, проходящей через 1м трубопровода в единицу времени от горячего теплоносителя к холодному при разности температур между ними в 1 ^оС.

Тогда можно записать следующее уравнение для теплового потока:

*
Q K_ц

l(t₁

t₂ )

(2.16)

Величину, обратную линейному коэффициенту теплопередачи, называют общим тепловым сопротивлением цилиндрической стенки:

К
R_ц ln

ц

. (2.17)

Необходимо рассмотреть понятие «критический диаметр изоляции». Тепловой изоляцией называют всякое покрытие

горячей поверхности, которое способствует снижению потерь теплоты в окружающую среду. Для тепловой изоляции используют материалы с низкой теплопроводностью – асбест, пробку, слюду, шлаковую и стеклянную вату, шерсть, опилки и т.д.

Анализ формулы полного термического сопротивления цилиндрической стенки (2.17) показывает, что тепловые потери уменьшаются пропорционально толщине изоляции. Для уменьшения расходов необходимо выбирать оптимальную толщину слоя изоляции. Для этого необходимо определить критический диаметр изоляции:

^dкр ^dиз ^,
где λ_кр - коэффициент теплопроводности изоляции, Вт/(м К);

- коэффициент теплоотдачи от наружной поверхности изоляции к окружающей среде, Вт/(м² К);

d_из ^{- наружный диаметр слоя изоляции, м.}

Практика эксплуатации тепловых аппаратов требует наилучших условий передачи теплоты от горячего теплоносителя к холодному. Для интенсификации теплопередачи необходимо стремиться уменьшить наибольшее сопротивление.

6. 
   Вопросы для самоконтроля
   

1. 
   Сформировать сущность закона Фурье.
   
2. 
   Что характеризует коэффициент теплопроводности и от каких факторов он зависит?
   
3. 
   Что такое условия однозначности?
   
4. 
   Что характеризует коэффициент температуропроводности?
   
5. 
   Охарактеризовать основные особенности процесса теплопроводности через плоскую и цилиндрическую стенку.
   
6. 
   Как определить общее термическое сопротивление многослойной стенки?
   
7. 
   Какова сущность коэффициентов теплоотдачи и теплопередачи, их отличие?
   
8. 
   Охарактеризовать основные особенности процесса теплопередачи через плоскую и цилиндрическую стенки.
   
9. 
   Что называют тепловой изоляцией?
   
10. 
    Что такое критический диаметр изоляции и как его можно определить?
    

2. 
   Конвективный теплообмен
   
   1. 
      Общие положения
      

Второй вид теплообмена – конвекция – происходит только в газах или жидкостях и состоит в том, что перенос теплоты осуществляется перемещающимися в пространстве объѐмами среды. Передача теплоты конвекцией всегда сопровождается теплопроводностью (при контакте, столкновении). Совместный процесс конвекции и теплопроводности называется конвективным теплообменом.

Интенсивность конвективного теплообмена, в первую очередь, зависит от режима движения жидкости или газа. Различают 3 режима движения:

ламинарный, когда частицы жидкости (газа) движутся параллельными потоками без поперечных перемещений, (например, спокойная равнинная река);

турбулентный режим, когда частицы жидкости (газа) движутся в разных направлениях и осуществляется интенсивное

перемешивание (например, горная река или сильно открытый водопроводный кран);

переходный режим.

Для определения режима движения используют безразмерный комплекс – число Рейнольдса: