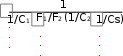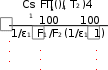39_tot (1)-конвертирован. Курс лекций по дисциплине теоретические основы теплотехники удк 621 016 Краткий курс лекций по дисциплине "Теоретические основы теплотехники" Учеб пособие А. А. Джамалуева, 2020. 127 с

• Название: Курс лекций по дисциплине теоретические основы теплотехники удк 621 016 Краткий курс лекций по дисциплине "Теоретические основы теплотехники" Учеб пособие А. А. Джамалуева, 2020. 127 с
• Дата: 28.12.2021
• Размер: 0.66 Mb.
• Имя файла: 39_tot (1)-конвертирован.docx
• Тип: Курс лекций; #320815
• страница: 8 из 11

100

где Сs=5.77 Вт/(м² К⁴) – коэффициент излучения абсолютно черного тела.

Тела, с которыми мы имеем дело на практике, излучают меньше тепловой энергии, чем абсолютно черное тело при той же температуре. Для характеристики реальных тел ввели понятие серого тела и серого излучения. Серое тело, как и абсолютно черное тело излучает энергию во всем диапазоне спектра длин волн, но интенсивность излучения меньше. Для сравнения используют коэффициент – степень черноты (ε):

ε = I_s / I_sλ = 0.004…0.96.

Степень черноты это отношение интенсивности излучения серого тела к интенсивности излучения абсолютно черного тела при той же температуре. Она показывает, какую часть энергии от абсолютного черного тела излучает реальное тело. Соответственно,

коэффициент излучения серого тела (С) всегда меньше коэффициента излучения абсолютно черного тела и определяется:

С = Е С_s.

Закон Стефана – Больцмана для реальных тел имеет следующий вид:

Е = ε E_s = ε C_s (T / 100)⁴ = C (T / 100)⁴.

Степень черноты изменяется для различных тел от 0 до 1 в зависимости от типа материала, состояния поверхности, температуры.

Закон Кирхгофа

Закон Кирхгофа устанавливает количественную связь между энергиями излучения и поглощения для серого и абсолютно черного тел.

Рассмотрим лучистый теплообмен между двумя параллельными поверхностями: абсолютно черной с температурой Ts и серой с температурой Т (рис. 2.17). Абсолютно черная поверхность излучает на серую энергию плотностью Еs. Часть этой энергии поглощается (А Еs), а часть – отражается на абсолютно черную (Еs – A E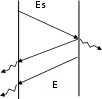s).
A Еs

Ts ^T
Рисунок 2.17 – Взаимный обмен энергией между черной и серой поверхностями

В свою очередь, серая поверхность излучает энергию плотностью Е, которая полностью поглощается абсолютно черной поверхностью.

Запишем баланс теплоты для серой поверхности: принятая энергия равна Es A, отданная - Е. Тогда плотность результирующего потока теплоты от серой поверхности

q = E – Es A .

Через некоторое время температуры поверхностей выравниваются, система тел находится в термодинамическом равновесии, тогда Ts=Т и q=0:

Е – Еs A = 0 или Е / А = Еs. (2.25)

Отношение энергии излучения к коэффициенту поглощения не зависит от природы тела и равно энергии излучения абсолютно черного тела при той же температуре.

Другой поверхностью может быть любое реальное тело, т.е. полученное уравнение справедливо для всех реальных тел и является математическим выражением закона Кирхгофа.

Из уравнения (2.25) видно: чем больше коэффициент поглощения, тем больше для этого тела и энергия излучения. Если тело мало излучает, то оно и мало поглощает. Абсолютно белое тело не способно излучать и поглощать энергию.

Из закона Кирхгофа также следует, что коэффициент черноты серого тела равен численно коэффициенту поглощения:

E/A = Es; E/Es = A; E/Es = ε; ε = A. Закон Ламберта

Количество энергии, излучаемой телом по всем направлениям, определяет закон Стефана – Больцмана. Однако интенсивность потока энергии зависит от направления. Эту зависимость

устанавливает закон Ламберта: максимальное излучение Ен имеет место в направлении нормали к поверхности.

Количество энергии, излучаемой под углом к нормали, Е пропорционально косинусу угла

Е =Ен cos (2.26)

Анализ уравнения (2.26) показывает, что максимальное излучение наблюдается при направлении лучей перпендикулярно к поверхности ( = 0; cos 0 = 1); интенсивность излучения вдоль поверхности равна нулю ( = 90; cos90 = 0).

3. 
   Теплообмен излучением между твердыми телами
   

При расчете лучистого теплообмена обычно рассматривается 2 случая:

теплообмен между двумя параллельными поверхностями; теплообмен между телами, когда одно из них находится

внутри другого.

Рассмотрим теплообмен между двумя параллельными поверхностями. Возьмем две серые параллельные пластины, разделенные прозрачной средой. Размеры пластин значительно больше расстояния между ними, так что излучение одной из них будет полностью попадать на другую. Первая пластина излучает на вторую поток энергии; вторая пластина часть этого потока поглощает, а часть отражает обратно на первую, где снова первая пластина часть энергии поглощает и часть излучает обратно на вторую и т.д.

Для упрощения расчетов необходимо использовать понятие эффективного (фактического) лучистого потока излучения, а точнее плотности интегрального излучения (Еэф):

Еэф = Е + R Епад.

Эффективное излучение - это сумма собственного и отраженного потоков энергии, испускаемых поверхностью данного тела. Оно зависит не только от физических свойств и температуры данного тела, но и от физических свойств, температуры и спектра излучения других окружающих тел. Кроме того, он зависит от формы, размеров и относительного расположения тел в пространстве.

Используя понятие эффективного излучения, легко определить плотность лучистого потока между параллельными поверхностями:

q C_пр

[( ^T1 )⁴

100

^{( T2 )4 ]}, (2.27)

100

где

^Cпр - приведенный коэффициент излучения, а

С₁,С₂, Сs- коэффициенты излучения 1-го, 2-го и абсолютно черного тела.

Вместо приведенного коэффициента излучения в расчетах можно применять приведенный коэффициент черноты системы тел (ε):

^Спр ^{= ε}пр ^Сs.

В этом случае уравнение (2.27) имеет вид

Cs[( ^T1 )⁴ ( ^T2 )⁴ ]

_q 100 100 _.

1/ε/ 1/ε/ 1

Полный тепловой поток соответственно равен:

F[( ^T1 ) ⁴

₍ T₂

) ⁴ ]

Cs F[( ^T1 ) ⁴

) ⁴ ]

_Q 100 100

100 _.

1/C₁ 1/C₂ 1/Cs

1/ε₁ 1/ε ₂ 1

Полный поток теплоты, передаваемой излучением от горячего тела более холодному, пропорционален поверхности тела, приведенному коэффициенту теплового излучения системы и разности четвертых степеней абсолютных температур тел.

Рассмотрим теплообмен между телами, когда одно из них (площадь поверхности F₁) находится внутри другого (площадь поверхности F₂). В этом случае часть излучения 2-й поверхности попадает на 1-ю поверхность; остальная энергия воспринимается самой же поверхностью. Количество излученной внутренним телом внешнему телу теплоты можно определить по предыдущему уравнению, если вместо F подставить поверхность меньшего тела F1, а приведенный коэффициент черноты системы определить по формуле
^ε пр
или приведенный коэффициент излучения системы:
С

пр .
Таким образом, полный поток теплоты можно определить следующим образом:






Q _.
Если 1-я поверхность мала по сравнению со 2-й поверхностью, то выражение F₁/ F₂ приближается к нулю, а уравнение теплообмена принимает вид:

1

1
Q C F [(^T1 ₁₀₀)⁴ (^T2 ₁₀₀)⁴ ] _.

Теплообмен между двумя произвольно расположенными телами может быть рассчитан по формуле

Q = φ ε_пр Сs F [(Т₁/100)⁴-(Т₂/100)⁴],

где φ - коэффициент облученности тела, учитывающий долю излучения первого тела, которая воспринимается вторым (приводятся в справочниках). Если все излучение одного тела попадает на другое, то φ = 1.

В приближенных расчетах величину приведенного коэффициента степени черноты (ε_пр) допустимо рассчитывать по формуле

ε_пр = ε₁ ε₂.

В различных областях техники довольно часто встречаются случаи, когда требуется уменьшить передачу теплоты потоком излучения. В этом случае используют установку экранов. Обычно экран представляет собой тонкий металлический лист с большой отражательной способностью.

Рассмотрим защитное действие экрана на примере. Две поверхности параллельны, причем Т₁>Т₂. Площади поверхностей и экрана считаем одинаковыми. Допускаем, что коэффициенты излучения поверхностей и экрана равны между собой. Тогда приведенные коэффициенты излучения между поверхностями без экрана, между 1-ой поверхностью и экраном и 2-ой поверхностью и экраном равны между собой.

Определим: плотность лучистого потока, передаваемого от 1-й поверхности ко 2-й без экрана, [уравнение ( 2.27)] -

q С [( ^T1 )⁴

₍ T₂

⁾4 ^] ; (2.28)

0 пр

100

100

плотность лучистого потока, передаваемого от 1-й поверхности к экрану -

q С [( ^T1 )⁴ ( ^Tэк )⁴ ] _;

1. 
   пр
   

100

100

плотность лучистого потока, передаваемого от экрана ко 2-й поверхности, -

q С [( ^Tэк )⁴

₍ T₂

)⁴ ] _.

2. 
   пр
   

100

100

При установившемся тепловом равновесии q₁ = q₂. Можно определить температуру экрана:
(Тэк/100)⁴=[(Т₁/100)⁴+(Т₂/100)⁴]/2.
Подставляя температуру экрана, получаем:

q С [( ^T1 )⁴

₍ T₂

⁾4 ^]/2 . (2.29)

1-2

^пр 100

100

Сравнивая уравнения( 2.28) и (2.29) находим, что установка одного экрана уменьшает передачу теплоты излучением в 2 раза:

q_1-2 = q₀ / 2 .

3. 
   Излучение газов
   

Излучение газообразных тел резко отличается от излучения твердых и жидких тел. Рассмотрим эти различия.

Излучение твердых и жидких тел зависит, в первую очередь, от состояния поверхности тела, а газы излучают энергию по всему объему, т.е. все частицы газа принимают участие в излучении.

Одно- и двухатомные газы (О₂, N₂, Ar, He и др.) обладают ничтожно малыми излучательной способностью и коэффициентом поглощения. Эти газы считаются прозрачными для тепловых лучей. Трех- и многоатомные газы (H₂O, CO₂, NO₂, SO₂ и др) обладают

значительной излучательной способностью, а следовательно, и коэффициентом поглощения.

В отличие от твердых тел газы излучают и поглощают энергию только на определенных длинах волн, т.е. излучение имеет селективный характер и спектр излучения несплошной (рис. 2.18). Это явление используют для определения состава газов.

Газы не подчиняются закону Стефана-Больцмана: их плотность излучения зависит от температуры не в 4-й степени, а во 2-й, 3-й и даже в дробной степени.

^Isλ


λ

Рисунок 2.18 – Селективный характер излучения газов Интенсивность излучения газов зависит от парциального

давления газа и толщины газового слоя. Расчет теплообмена излучением между газом и стенками канала очень сложен и выполняется с помощью целого ряда графиков и таблиц. Более простой и вполне надежный метод расчета разработан Шаком, который предложил уравнения для поверхностной плотности лучистого потока газов в среде с температурой 0 К:

q 8.78 ³

PS( ^T

₎3 .5_;

СО₂

100