39_tot (1)-конвертирован. Курс лекций по дисциплине теоретические основы теплотехники удк 621 016 Краткий курс лекций по дисциплине "Теоретические основы теплотехники" Учеб пособие А. А. Джамалуева, 2020. 127 с

• Название: Курс лекций по дисциплине теоретические основы теплотехники удк 621 016 Краткий курс лекций по дисциплине "Теоретические основы теплотехники" Учеб пособие А. А. Джамалуева, 2020. 127 с
• Дата: 28.12.2021
• Размер: 0.66 Mb.
• Имя файла: 39_tot (1)-конвертирован.docx
• Тип: Курс лекций; #320815
• страница: 7 из 11

wl

Re=
, (2.18)

где w - средняя скорость жидкости или газа, м/с;

l - характерный размер, для круглой трубы это диаметр d, для канала – эквивалентный диаметр d _экв = 4F/ П (F – площадь поперечного сечения канала, П - полный периметр сечения, независимо от того, какая часть этого периметра участвует в теплообмене);

ν - коэффициент кинематической вязкости, м²/с.

При числах Рейнольдса (Re), меньших 2000, режим считается ламинарным, при значениях числа Рейнольдса, больших 10000, – режим движения турбулентный; при 200 Re 10000 – режим переходный.

Большое влияние на теплообмен оказывают следующие физические параметры теплоносителей: коэффициент теплопроводности, теплоемкость, плотность, температуропроводность, вязкость. В конвективном теплообмене большое значение имеет вязкость. Все реальные жидкости обладают вязкостью: между частицами или слоями, движущимися с различными скоростями, всегда возникает сила внутреннего трения

, ускоряющая движение более медленного слоя и тормозящая движение более быстрого. Вязкость – это способность жидкости или газа противостоять движению (перемещению) одного слоя жидкости (газа) относительно другого.

Теоретическое рассмотрение задач конвективного теплообмена основывается на использовании теории пограничного слоя, разработанной австрийским физиком Прандтлем.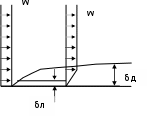

Рассмотрим движение жидкости вдоль какой-либо поверхности со скоростью , одинаковой по всей толщине (рис. 2.7).





Рисунок 2.7 – Образование динамического пограничного слоя при обтекании поверхности

При перемещении жидкости вдоль поверхности за счѐт вязкости частицы жидкости прилипают к поверхности и тормозят движение жидкости, что приводит к изменению скорости движения жидкости по толщине слоя. Скорость изменяется от начальной w до нуля (возле стенки). Слой жидкости возле поверхности, в котором происходит изменение скорости жидкости от исходного значения вдали от стенки до нуля непосредственно возле стенки, называют динамическим пограничным слоем. Толщина этого слоя δ_д возрастает вдоль по потоку. Толщина слоя зависит от скорости движения жидкости или газа и от вязкости.

Режим течения жидкости в пограничном слое может быть и турбулентным и ламинарным (характер определяется числом Re). Но в любом случае непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Его называют ламинарным подслоем – δ_л.

Если температуры стенки и жидкости неодинаковые, то вблизи стенки образуется тепловой пограничный слой , в котором происходят все изменения температуры: от начальной t_ж до температуры стенки t_ст (рис. 2.8)._. Пограничный слой уменьшает интенсивность теплообмена, т.к. тепло распространяется в нѐм преимущественно за счѐт теплопроводности, которая у жидкостей и газов мала. Для интенсификации необходимо, в первую очередь, увеличить скорость движения жидкости или газа, при этом мы перейдѐм от теплопроводности к конвенции.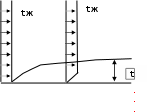





ние те
^tст

Рисунок 2.8 – Образова плового пограничного слоя

В общем случае толщины теплового и динамических слоѐв могут не совпадать. Соотношение толщины динамического и теплового пограничных слоѐв определяется безразмерным числом Прандтля:

Pr = /а, (2.19)

где а – коэффициент температуропроводности, м²/с, – коэффициент кинематической вязкости, м²/с.

Для вязких жидкостей с низкой теплопроводностью (например, масел) Pr > 1 и, следовательно, δ_д > δ_т; для газов - Pr 1, δ_д δ_т; для жидких металлов - Pr < 1 и δ_т > δ_д.

2. 
   Моделирование конвективного теплообмена
   

Конвективный теплообмен, в отличие от теплопроводности, описывается несколькими дифференциальными уравнениями с большим количеством переменных параметров. Поэтому решение вопросов конвективного теплообмена вызывает большие трудности. В связи с этим чаще всего используют изучение процесса путѐм проведения эксперимента. По экономическим или техническим причинам это тоже не всегда возможно. Поэтому используют исследование процессов на уменьшенных моделях – т.е. моделирование процесса. Для получения достоверных результатов при моделировании необходимо выполнить 2 условия:

Процессы, которые осуществляются в натуральном агрегате и модели, должны иметь одинаковую физическую природу и описываются подобными дифференциальными уравнениями. Например, теплопроводность хорошо моделируется электрическим током (электропроводностью), т.к. физическая природа одинакова – электроны;

Необходимо соблюдение геометрического подобия модели и натурального агрегата, а также подобия температур и скоростей.

Геометрическое подобие осуществляется легко путем уменьшения в масштабе, а остальные виды подобия достичь намного сложнее, необходимо локальное моделирование.

Для выполнения этих условий используют теорию подобия. Теория подобия объединяет положительные стороны математического и экспериментального методов исследования процессов. Понятие подобия впервые было введено в геометрии. В дальнейшем оно было расширено и нашло применение при изучении физических явлений. Геометрическое подобие является обязательной предпосылкой подобия физических явлений.

Рассмотрим подобие скоростей на примере трубы, по которой движется газ (рис. 2.9).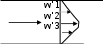





Рисунок 2.9 – Подобие скоростей

Скорости потоков считаются подобными, если выполняется соотношение,

w

w
/ /

1 2


w

w
// //

1 2

/ /


w

w
3 4


w

w
// //

3 4
...

/


w
n _.


w
// n

Таким же образом устанавливается подобие и других параметров конвективного теплообмена: плотности, вязкости и т.д.

Два процесса конвективного теплообмена считаются подобными, если подобны все параметры, характеризующие конвективный теплообмен. Для упрощения процесса установления подобия используют безразмерные комплексы физических параметров. Если эти комплексы для модели и натурального агрегата одинаковы, то процессы считаются подобными. Эти комплексы называют числами или критериями подобия и им присвоили имена известных учѐных. Чисел подобия много. Для конвективного теплообмена используют пять чисел подобия. Рассмотрим эти числа подобия.

Число Рейнольдса

Число Рейнольдса [уравнение (2.18)] характеризует режим течения жидкости или газа и выражает отношение сил инерции (скоростного напора) к силам вязкостного трения.

При малых значениях числа Рейнольдса преобладают силы вязкости и режим течения ламинарный (отдельные струи потока не перемешиваются, двигаясь параллельно друг другу, и всякие

случайные завихрения быстро затухают под действием сил вязкости). При турбулентном течении в потоке преобладают силы инерции, поэтому завихрения сильно развиваются.

Число Прандтля

Число Прандтля [уравнение (2.19)] устанавливает соотношение между толщиной динамического и теплового пограничных слоѐв.

Число Нуссельта

Число Нуссельта характеризует интенсивность конвективного теплообмена между жидкостью (газом) и поверхностью твѐрдого тела:
^Nu , (2.20)

где α- коэффициент теплоотдачи, Вт/(м² К); l – характерный размер, м;

- коэффициент теплопроводности газа или жидкости, Вт/(м К).

Число Грасгофа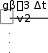

Число Грасгофа характеризует интенсивность свободного конвективного теплообмена, который обусловлен тем, что более нагретые частицы жидкости (газа) выталкиваются холодными вверх за счѐт влияния силы тяжести:
Gr

, (2.21)
где g = 9,81 м/с² – ускорение свободного падения;

• 
  коэффициент температурного расширения, 1/ К: для жидкостей приведены в справочниках, для газов - = 1/Т;
  

l – характерный размер, м;

t – разница температур частиц жидкости (газа);

• 
  кинематическая вязкость, м²/с.
  

Число Грасгофа характеризует отношение подъѐмной силы, возникающей вследствие теплового расширения жидкости (газа), к силам вязкости.

Число Эйлера

Число Эйлера характеризует отношение перепада давления к скоростному напору:
^Еu , (2.22)
Р – перепад давления на рассматриваемом участке канала, Па;

• 
  плотность жидкости (газа), кг/м³; скорость жидкости (газа), м/с.
  

При проектировании теплообменных аппаратов необходимо

определить два параметра: коэффициент теплоотдачи и перепад давления p.Они входят в числа Нуссельта и Эйлера, т.е. это определяемые числа подобия. Числа Рейнольдса Re, Грасгофа Cr и Прандтля Pr являются определяющими.

Уравнения подобия – зависимость между определяемым числом подобия и определяющими числами подобия. Таким образом, при моделировании основной целью является нахождение уравнений:

Nu = f₁(Re,Pr,Gr),

Eu = f₂(Re,Pr,Gr).

Рассмотрим некоторые частные случаи:

Если теплообмен вынужденный и режим движения турбулентный, то свободная конвекция практически не влияет на теплообмен, поэтому исключают число Грасгофа Gr:

Nu=f₃(Re, Pr).

Если вынужденный теплообмен осуществляется между газом и телом, то исключают число Прандтля Pr, т.к. для газов он равен единице:

Nu=f₄(Re).

Если теплообмен естественный (свободный), то из уравнения исключается число Рейнольдса, поскольку скорость естественного движения теплоносителя вдоль поверхности неизвестна и число Рейнольдса переходит в разряд определяемых:

Nu=f₅(Gr, Pr).

Исследованиями установлено, что при одинаковой разности температур интенсивность теплообмена (значение коэффициента теплоотдачи α) зависит от направления теплового потока: к телу или от тела (нагрев или охлаждение). Академик Михеев М.А. предложил учитывать направление теплового потока отношением

₍ ^Prж ₎^0.25 _,

Pr_ст

где Pr_ж – число Прандтля для жидкости при еѐ температуре; Pr_ст – число Прандтля для жидкости при температуре стенки.

Тогда общее уравнение подобия для конвективного теплообмена принимает вид

Nu = c Reⁿ Pr^m Gr^d (Pr_ж / Pr_ст)^0.25, (2.23)
где c, n, m, d – коэффициенты, которые определяются экспериментальными исследованиями.

3. 
   Теплообмен при ламинарном режиме течения жидкости в круглых трубах
   

Изучение процесса теплоотдачи в трубах представляет большой практический интерес, т.к. трубы являются элементом различных теплообменных аппаратов.

Рассмотрим особенности движения жидкости в трубе при ламинарном режиме – Re < 2000.

При движении жидкости вдоль трубы у стенок образуется динамический пограничный слой, толщина которого по течению возрастает и становится равной радиусу трубы. В этом месте пограничный слой заполняет собой всѐ сечение трубы и в ней устанавливается постоянное распределение скоростей, характерное для данного режима течения (см. рис. 2.10).




^wmax

Рисунок 2.10 – Изменение скорости при ламинарном режиме движения
В расчѐтах используют среднюю скорость, которая равна половине от максимальной:

= ½ _max.

Участок трубы, на котором устанавливается толщина пограничного слоя и, соответственно, постоянное распределение

скоростей, называется участком стабилизации течения. Его величина составляет:

l_ст = 50 d.
Аналогично изменяется и толщина теплового пограничного слоя, что приводит к уменьшению коэффициента теплоотдачи: у входа в трубу он имеет максимальное значение, затем убывает и на участке стабилизации принимает определѐнное среднее значение, которое остаѐтся неизменным по всей длине трубы, т.к. влияние отдельных факторов по длине сглаживается (рис. 2.11).

Возможны 2 вида ламинарного течения: вязкостное;

вязкостно-гравитационное.

α


^lст
Рисунок 2.11- Изменение коэффициента теплоотдачи по длине трубы
Вязкостный режим наблюдается в жидкостях с большим коэффициентом вязкости, при этом режиме нет перемешивания слоѐв, свободная конвекция не влияет на теплообмен, перенос теплоты осуществляется теплопроводностью (например, мазут).

Вязкостно-гравитационный режим характерен для маловязких жидкостей и газов; наблюдается перемешивание слоѐв, т.е. имеет место свободная конвекция. Важное значение при этом имеет направление свободной и вынужденной конвекции. Возможны 3 случая:

направления совпадают – теплообмен улучшается за счѐт увеличения скорости жидкости;

направления противоположные – теплообмен ухудшается за счѐт уменьшения скорости жидкости;

направления взаимно перпендикулярны – теплообмен улучшается за счет перемешивания жидкости.

Уравнение подобия для вязкостного режима –

Nu = 0.15 Re^0.33 Pr^0.43 (Pr_ж / Pr_ст)^0.25.
Уравнение подобия для вязкостно-гравитационного режима –
Nu = 0.15 Re^0.33 Pr^0.43 Gr^0.1 (Pr_ж / Pr_ст)^0.25
или в случае, когда теплоносителем является не жидкость, а газ, для которого число Прандтля примерно равно единице (Pr = 0,7), уравнение принимает вид
Nu = 0.13 Re^0.33 Gr^0.1.
Вязкостно-гравитационный режим имеет место при величине (Gr Pr) > 8*10⁵. Параметры теплоносителя выбираются при

температуре t = 0,5 (t₀ + t_ст), где t₀ – температура жидкости на входе в трубу.

Формулы справедливы при отношении l / d > 50. Для труб, имеющих длину l < 50d, значение коэффициента теплоотдачи α, полученное из данных формул, следует умножить на поправочный коэффициент ε_l (табл. 2.1).
Таблица 2.1 - Поправочный коэффициент для расчета теплообмена в трубах длиной менее 50 диаметров

l/d	1	4	5	10	15	20	30	40	50
εl	1.9	1.7	1.44	1.28	1.18	1.13	1.05	1.02	1

По рассмотренным формулам определяется число Нуссельта, а по нему – коэффициент теплоотдачи α:


,
где λ – коэффициент теплопроводности, Вт/(м К);

^ - характерный размер, м.

4. 
   Теплообмен при турбулентном и переходном режимах
   

При турбулентном режиме ( Re >10000) также устанавливается пограничный слой и размеры участка стабилизации такие же, как и при ламинарном движении. Но в связи с более сложным строением потока изменение скорости потока по сечению трубы сильно изменяется: наиболее резко скорость потока изменяется вблизи стенки, а в средней части сечения скорость почти не изменяется. В расчѐтах пользуются средними скоростями:

= 0,8 … 0,9 _max,

где max – максимальная скорость, которая наблюдается на оси трубы.

При турбулентном потоке жидкость весьма интенсивно перемешивается и естественная конвекция практически не оказывает влияния, поэтому из уравнения подобия исключено число Грасгофа.

Для определения среднего коэффициента теплоотдачи при развитом турбулентном режиме (Re > 10⁴), когда l/d > 50, М.А. Михеев рекомендует следующее уравнение подобия:

Nu = 0.021 Re^0.8 Pr^0.43 (Pr_ж / Pr_ст)^0.25.

Для воздуха (при Pr 0,7) эта формула упрощается:

Nu=0.18Re^0.8.

Для труб, имеющих отношение l/d < 50, коэффициент теплоотдачи выше, поэтому значение α, полученное из данных уравнений, следует умножить на поправочный коэффициент, зависящий от числа Рейнольдса и отношения l/d / 1 /.

При теплообмене в изогнутых трубах (змеевиках) вследствие центробежного эффекта в поперечном сечении трубы возникает вторичная циркуляция, наличие которой приводит к увеличению

коэффициента теплоотдачи. Поэтому коэффициент α, полученный по данным уравнениям, следует умножить на поправочный коэффициент:

ε_зм = 1.0+3.6 d/D,

где d – диаметр трубы, м;

D – диаметр спирали змеевика, м.

Переходный режим движения характеризуется: 2000 < Re < 1000. Теплоотдача при этом режиме зависит от очень многих величин, трудно поддающихся учѐту, и поэтому не может быть описана одним уравнением подобия. В этом случае используют комплекс К_о:
K_o=Nu Pr^{- 0.43}(Pr_ж / Pr_ст)^{- 0.25}. (2.24)
Величина комплекса К_о зависит от чисел Рейнольдса Re и Грасгофа Gr. Эта зависимость представлена на рис. 2.12.

Ко

Gr =10⁶
Gr = 10⁴

Gr = 10²

Gr = 10⁰

Re
Рисунок 2.12 – Зависимость комплекса Ко от чисел Рейнольдса и Грасгофа

Как видно из рис.2.12, в области переходного режима опытные точки не объединяются единой зависимостью. С увеличением Re теплоотдача возрастает, причем существенное влияние оказывает естественная конвекция. Чем больше число Грасгофа, тем больше комплекс К_о и, следовательно, коэффициент теплоотдачи. При развитом турбулентном режиме все кривые сливаются в одну линию.

В связи с тем, что до сих пор удовлетворительного метода расчѐта теплоотдачи для переходной области нет, определение коэффициента теплоотдачи α может быть произведено только приближенно с помощью уравнения подобия (2.24) и графика (см. рис. 2.12).

5. 
   Теплообмен при поперечном омывании одной трубы и пучка труб
   

Процесс теплоотдачи при поперечном потоке жидкости, омывающей одиночную трубу, характеризуется рядом особенностей. Плавное, безотрывное омывание поверхности круглой трубы наблюдается только при Re < 5. При больших значениях Рейнольдса условия омывания лобовой и кормовой половины трубы совершенно различны. При этом важную роль

играет угол атаки. Угол атаки ( – угол между направлением

движения основного потока и радиусом, который соединяет точку на поверхности трубы с центром трубы. При Re > 5 в лобовой части трубы (при = 0) поток раздваивается, толщина пограничного слоя практически равна 0. При движении потока по периметру трубы развивается пограничный слой, толщина его увеличивается и достигает max при = 90⁰. Потом этот слой начинает разрушаться (смывается потоком жидкости), толщина слоя уменьшается. В

кормовой части омывание носит сложный вихревой характер, при этом происходит разрушение пограничного слоя.

Такая своеобразная картина движения при поперечном обтекании трубы в значительной мере отражается на коэффициенте теплоотдачи по окружности трубы (рис. 2.13).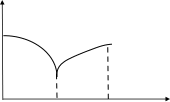
α_φ/α_ср

0 90 180 φ^о
- коэффициент теплоотдачи в данной точке; – средний

коэффициент теплоотдачи по поверхности трубы, Вт/м² К Рисунок 2.13 – Изменение коэффициента теплоотдачи по

периметру трубы

Максимальный коэффициент теплоотдачи при угле атаки = 0⁰ (т.к. в лобовой части жидкость непосредственно контактирует с трубой). Потом α уменьшается, т.к. увеличивается толщина пограничного слоя. Затем α увеличивается, т.к. пограничный слой исчезает и кормовая часть омывается вихревыми потоками.

Средний коэффициент теплоотдачи определяется из следующих уравнений подобия:

а) при Re = 5…1000 –

Nu = 0.5 Re^0.5 Pr^0.38 (Pr_ж / Pr_ст)^0.25,
если теплоноситель - воздух (газ),

Nu=0.43 Re^0.5;
б) при Re = 1000…200000 –

Nu = 0.25 Re^0.6 Pr^0.38 (Pr_ж / Pr_ст)^0.25,
если теплоноситель - воздух (газ),

Nu=0.216 Re^0.6.
Сложная гидродинамическая картина омывания одиночной трубы делается ещѐ более сложной при омывании пучка круглых труб. Теплообменные аппараты, состоящие из пучка труб и омывающиеся поперечным потоком жидкости, имеют в технике большое распространение. Применяются в основном два вида расположения труб в пучках: коридорный и шахматный.

Основными характеристиками пучка труб являются:

• 
  внешний диаметр трубы – d;
  
• 
  количество труб в одном ряду – n_ш;
  
• 
  количество рядов труб - n_p;
  
• 
  отношение расстояния между осями труб по ширине пучка к внешнему диаметру труб – S₁/d;
  
• 
  отношение расстояния между осями двух соседних рядов к внешнему диаметру труб – S₂/d.
  

От расположения труб в значительной степени зависят характер движения жидкости, омывание труб каждого ряда и в целом теплообмен в пучке. Если в канале было турбулентное

движение жидкости, то оно будет турбулентным и в пучке труб, причѐм степень турбулизации будет возрастать от ряда к ряду, т.к. пучок труб является очень хорошим турбулирующим устройством. Если в канале перед пучком режим течения был ламинарный, то в зависимости от числа Рейнольдса в пучке труб может быть как ламинарное, так и турбулентное течение жидкости.

Рассмотрим характер обтекания труб при различных расположениях труб в пучке. Омывание труб первого ряда, независимо от расположения труб в пучке, практически не отличается от омывания одиночной трубы и зависит от начальной турбулентности потока. Характер омывания следующих рядов труб в обоих пучках изменяется. При коридорном расположении трубы любого ряда затеняются трубами предыдущего ряда, что ухудшает омывание лобовой части, и большая часть поверхности находится в слабой вихревой зоне. При шахматном расположении загораживание одних труб другими не происходит для всех последующих рядов. Трубы третьего ряда при коридорном расположении также изменяют характер теплообмена, а после третьего ряда характер не изменяется, т.е. наступает стабилизация. Коэффициент теплоотдачи в зависимости от угла атаки для любого ряда шахматного расположения в лобовой части имеет максимальное значение и изменения его мало отличаются от изменения коэффициента α для одиночной трубы. Такое же изменение коэффициента теплоотдачи имеет место и для первого ряда коридорного расположения пучка (рис. 2.14). Для труб второго ряда максимум приходится на φ = 50 – 60⁰. Теплообмен как лобовой, так и кормовой части трубы меньше, чем теплообмен

одиночной трубы.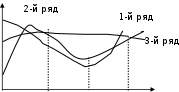

При любом расположении труб каждый ряд вызывает дополнительную турбулизацию потока, поэтому α для труб второго ряда больше, чем для первого, а для третьего - выше, чем для второго. Начиная с третьего ряда, поток жидкости стабилизируется и коэффициент α для всех последующих рядов остается const.

α_φ/α_ср

0 90 180 φ
Рисунок 2.14 – Изменение коэффициента теплоотдачи для различных рядов пучка труб
Если теплоотдачу третьего ряда принять за 100%, то теплоотдача первого ряда коридорного и шахматных пучков составляет лишь 60%; теплоотдача второго ряда коридорного пучка составляет 90%, шахматного – 70%. В целом теплоотдача в шахматных пучках за счет лучшей турбулизации потока выше, чем в коридорных. Это свойство широко используют при конструировании теплообменных аппаратов. Недостаток шахматной схемы – трудность изготовления.

При расчете теплообменных аппаратов используют уравнения подобия:

Nu = f (Re, Pr, E_s),

где E_s – поправочный коэффициент, учитывающий расстояние между трубами: для коридорного расположения -E_s = (S₂/d)^-0,15; для шахматного расположения пучка труб - при S₁/S₂ < 2 E_s = (S₁/S₂)^0,166; при S₁/S₂ 2 E_s = 1,12.

6. 
   Теплообмен при свободном движении теплоносителя (естественная конвекция)
   

Свободным называется движение жидкости (газа), возникающее вследствие разности плотностей нагретых и холодных еѐ частей. Теплообмен при свободном движении, или естественная конвекция, возникает у нагретых стен печей, у нагревательных приборов систем отопления, при кипении в большом объеме и др. Естественная циркуляция (а соответственно и естественный теплообмен) будет проходить тем интенсивнее, чем больше температурный напор ( t = t_ст - t_ж) и больше длина (высота) поверхности, вдоль которой происходит теплообмен.

Рассмотрим некоторые особенности теплообмена при свободном движении, протекающего между нагретой вертикальной плитой и жидкостью. При движении жидкости вдоль плиты возникает, как известно, пограничный слой. Его толщина растет по направлению движения жидкости. В начале движения толщина его мала и движение имеет ламинарный характер. На некотором расстоянии от нижнего края плиты ламинарный слой начинает разрушаться, движение становится неустойчивым, а затем переходит в турбулентное. В соответствии с изменением пограничного слоя и характера движения жидкости изменяется коэффициент теплоотдачи.

Около нагретой горизонтальной плиты движение жидкости имеет иной характер и зависит от положения и размеров плиты.

Михеев М.А., изучая теплоотдачу в неограниченном пространстве для тел любой формы и размера, расположенных горизонтально и вертикально, получил уравнение подобия:

Nu = C (Gr Pr)ⁿ,

где с, n – коэффициенты, зависящие от величины комплекса Gr Pr (табл.2.2).

Таблица 2.2 -Значения коэффициентов в уравнении Михеева

Gr Pr	10-3…5 102	5 102…2 107	2 107
c	1.18	0.54	0.135
n	1/8	1/4	1/3

Физические константы, входящие в состав чисел подобия, определяют по средней температуре t = 0,5 (t_ж + t_cт). В качестве определяющего размера в числах Нуссельта и Грасгофа приняты для труб и шаров их диаметр, для плит, пластин, вертикальных труб

– высота.

Для расчета теплообмена от горизонтальной плиты, обращенной греющей стороной вверх, значение коэффициента теплоотдачи α увеличивают на 30%. Если греющая сторона обращена вниз, то значение α следует уменьшить на 30%. В обоих случаях определяющим является наименьший размер плиты в плане.

При ламинарном движении около горизонтальных труб рекомендуется формула Михеевой (при 10³ < Gr Pr <10⁸):

Nu = 0,5 (Gr Pr)^0,23 (Pr/Gr_ст)^0,25.

Определяющим размером является диаметр трубы, определяющей температурой – температура газа или жидкости вдали от трубы.

Довольно часто приходится рассчитывать теплообмен естественной конвекцией в узких глухих каналах (например, перенос тепла между оконными стеклами,. Типичные случаи теплоотдачи приводятся в справочниках, там же приведены данные по их расчету /1/.

При (Gr Pr) < 10³ естественную конвекцию можно не учитывать.

7. 
   Вопросы для самоконтроля
   

1. 
   Как определить режим течения жидкости или газа?
   
2. 
   Какое влияние на теплообмен оказывает образование динамического и теплового пограничных слоев?
   
3. 
   Чем вызвана необходимость моделирования конвективного теплообмена?
   
4. 
   Охарактеризовать условия для получения достоверных результатов при моделировании процесса.
   
5. 
   Какие числа подобия описывают конвективный теплообмен?
   
6. 
   Что такое уравнения подобия и как их получают?
   
7. 
   Охарактеризовать основные особенности теплообмена в круглых трубах при ламинарном и турбулентном режимах.
   
8. 
   Как проводится расчет теплообмена в круглых трубах при переходном режиме?
   
9. 
   Охарактеризовать особенности теплообмена при омывании одиночной трубы и пучка труб.
   
10. 
    Какая схема расположения труб в пучке наиболее эффективна и почему?
    
11. 
    При каких условиях происходит естественная конвекция? Какие особенности она имеет?
    
12. 
    Как производится расчет процессов теплообмена при свободном движении жидкости или газа?
    

3. 
   Теплообмен излучением
   
   1. 
      Общие положения
      

Теплообмен излучением (лучистый теплообмен) свойственен всем телам, температура которых не равна абсолютному нулю. Источником излучения является внутренняя энергия тела. Тепловое излучение есть результат превращения внутренней энергии тела в энергию электромагнитных колебаний. Излучение осуществляется в 3 этапа:

превращение внутренней энергии в энергию электромагнитных

волн;


распространение электромагнитных волн в пространстве; поглощение электромагнитных волн другим телом.

Тепловое излучение, как процесс распространения

электромагнитных волн, характеризуется длиной волны (в метрах) и частотой колебаний (в герцах). При этом волны распространяются со скоростью света с=3*10⁸ м/с, а частота колебаний и длина волны связаны между собой - =с/

Все виды электромагнитного излучения имеют одинаковую природу, поэтому классификация излучения по длинам волн в зависимости от производимого ими эффекта носит лишь условный характер. При температурах, с какими обычно имеют дело в технике, основное количество энергии излучается при =0,8…40

(80) мкм. Эти лучи принято называть тепловыми (инфракрасными). Большую длину волны имеют радиоволны, меньшую – волны видимого (светового) излучения - =0,4…0,8 мкм; если <0,4 мкм, излучение называют ультрафиолетовое.

Энергия, излучаемая всем телом по всем направлениям и длинам волн, называется интегральным излучением, обозначается Q и измеряется в ваттах.

Интегральное излучение, приходящееся на единицу поверхности, называется плотностью интегрального излучения, Вт/м²:
E _.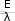

Интенсивность интегрального излучения – это отношение плотности интегрального излучения к длине волны, Вт/м³:

I _.
Все тела не только излучают энергию (способность излучать энергию определяется природой данного тела и его температурой), но и поглощают, отражают и пропускают через себя падающие лучи от другого тела (рис. 2.15).

_QR Q





Рисунок 2.15 – Распределение энергии излучения, падающей на тело
Часть энергии излучения (Q), падающей на тело, поглощается (Q_A), часть отражается (Q_R), а часть протекает сквозь него (Q_D). Таким образом, можно записать:

Q = Q_A + Q_R + Q_D.

Разделим полученное уравнение на Q:

A + R + D = 1,

где A = Q_A/Q - поглотительная способность тела, это отношение энергии, поглощенной телом, ко всей падающей энергии; величину А называют коэффициентом поглощения;

R = Q_R/Q - отражательная способность тела, это отношение энергии, отраженной телом, ко всей падающей энергии; величину R называют коэффициентом отражения;

D = Q_D/Q - способность тела пропускать энергию излучения; величину D называют коэффициент пропускания.

Тело, поглощающее все падающее на него излучение, называется абсолютно черным:

А = 1; R = D = 0.

Тело, отражающее все падающее на него излучение, называется абсолютно белым:

R = 1; A = D = 0.

Тело, пропускающее все падающее на него излучение, называется абсолютно прозрачным:

D = 1; A = R = 0.

В природе абсолютно черных, белых и прозрачных тел не существует, тем не менее понятие о них является очень важным для сравнения с реальными поверхностями.

Если поверхность поглощает тепловые лучи, но не поглощает световые, она не кажется черной. Более того, наше зрение может воспринимать такую поверхность как белую, например снег, для которого А=0,98. Стекло, прозрачное в видимой части спектра, почти не прозрачно для тепловых лучей (А=0,94). Свойство тел поглощать или отражать тепловые лучи зависит в основном от состояния поверхности, а не от цвета.

2. 
   Основные законы лучистого теплообмена
   

Закон Планка

Интенсивность излучения абсолютно черного тела I_s и любого реального тела I зависит от температуры и длины волны:

_C 5

_Is 1 <sub>,

e</sub>C₂ T₁
где I_sλ – интенсивность излучения абсолютно черного тела, Вт/м³; С₁=3,74*10^-16 Вт/м² – первая постоянная Планка;

С₂=1,44*10^-2 м К – вторая постоянная Планка;

- длина волны, м;

Т – абсолютная температура, К;

е– основание натурального логарифма.

Графически этот закон представлен на рис. 2.16.


I_s

λ, м
Рисунок 2.16 – Зависимость интенсивности излучения от длины волны при различных температурах
Из рис. 2.16 видно, что при увеличении длины волны интенсивность излучения сначала растет, достигая максимальной величины, а потом уменьшается; для каждой длины волны с увеличением температуры увеличивается интенсивность излучения; при увеличении температуры максимумы кривых смещаются в сторону более коротких волн. Длина волны в микрометрах,

отвечающая максимальному значению интенсивности излучения, определяется законом смещения Вина:

max = 2,9 / Т, где Т – абсолютная температура, К. Закон Стефана – Больцмана

На основании опытных данных Стефан установил, что плотность интенсивности излучения абсолютного черного тела (Е_s) пропорциональна четвертой степени абсолютной температуры. Больцман получил этот закон теоретическим путем, исходя из 2-го закона термодинамики:

Е_s = σ T⁴,

где ζ - постоянная Стефана-Больцмана; ζ =5,77*10^-8 Вт/(м² К⁴). Для технических расчетов закон Стефана-Больцмана обычно записывают в виде

Es Cs(

T _{)4 ,}