Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов

• Название: Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов
• Дата: 08.07.2018
• Размер: 2 Mb.
• Имя файла: Lektsii_diskr_matem_konspekt.doc
• Тип: Документы; #48405
• страница: 4 из 8

(См. задачи к Гл. 1 из Зверовича (файл zvtrovich1.pdf в папке «дискретная математика) на стр. 26)

3. 
   Соответствия и отношения.
   

1. 
   Соответствия.
   

Пусть даны множества X и Y. Будем говорить, что задано соответствие R из X в Y, если для каждого элемента x множества X указано подмножество R(x)⊂Y соответствующих ему элементов множества Y (возможно, пустое).

Формально соответствие R из множества X в множество Y можно определить как подмножество декартова произведения X×Y, считая, что (x,y)∈R, если y∈R(x).

На основании этого определения можно записать
R={(x;y)|xA, yB}(A×B).
Иногда правило соответствия удобно записывать в операторной форме r:АВ, где r-оператор соответствия.
Область определения соответствия из множества X в множество Y – это множество всех первых компонент упорядоченных пар из R:
δ_R =
Область значения соответствия R – это множество всех вторых компонент упорядоченных пар из R:

ρ_R =
Из определения вытекает, что δ_R, ρ_R. Соответствие из X в Y называется всюду определенным, если его область определения совпадает с множеством А: δ_R = Х.
Сечением соответствия для фиксированного элемента называется множество . Эта формула читается так: множество всех «образов» элемента х при данном соответствии.
Сечением соответствия R по множеству будем называть множество
П р и м е р 4.1.1. Рассмотрим множество программистов А={И,П,С} и множество программ В = {n₁, n₂, n_3, n_4, n₅}. Зададим соответствие R из А и В, связывающее программистов и разрабатываемые ими программы:

R = {(И, n₁), (И,n₃), (И, n₅), (П,n₂), (П,n₄), (С,n₂), (С,n₅)}⊆ А×В.

Область определения соответствия R в этом примере есть все множество А, а область значения – все множество В. Сечением соответствия R по элементу П будет множество

R(П) = {n₂, n₄}.
На рис. 2 наглядно показан пример соответствия из A={x₁, x₂,..x₆}в B={y₁, y₂,..y₆} для пар {(x_i, y_j)| x_iA, y_jB}. Проекция на первую компоненту пары 1{(x, y)} формирует область определения A0={x₁, x₃, x₄, x₅, x₆}A, а на вторую компоненту 2{(x, y)} - область значений B0={y₁, y₂, y₄, y₆}B. Элементы y_jB называют образом элемента х_iA, а элемент х_iA - прообразом элемента y_jB.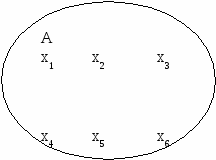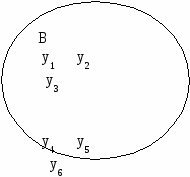












Рис. 2 Отображение элементов множества A на множество B.
Например, на рис.2 образом для x₁ является y₁, для x₂ - , для x₃ – {y₁, y₂}, для x₄ - y₆, для x₅ – y₄, для x₆ – y₄, прообразом для y₁– {x₁, x₃}, для y₂ – x₃, для y₃ = , для y₄ – {x₅, x₆}, для y₅ - , для y₆ – x₄.

Примером соответствия может служить также англо-русский словарь:

capacity – способность, мощность, емкость.

Понятие соответствия обобщает понятие функции. Если каждое множество R(x) содержит ровно один элемент, то соответствие R называется функциональным. Всякое функциональное соответствие R определяет отображение множества X в множество Y, при котором произвольному элементу x множества X соответствует единственный элемент множества R(x). Допуская небольшую вольность, будем обозначать это отображение также через R.
П р и м е р ы 4.1.2.
1) Натуральному числу x поставим в соответствие совокупность его простых делителей. Тем самым определяется соответствие R из множества натуральных чисел в множество простых чисел. Имеем R(10)={2, 5}, R(30)={2, 3, 5}, R(7)={7}, R(1)=∅.

2) Пусть A – множество участников рынка, а T – множество товаров. Для каждого товара t указана его цена p, для каждого участника ранка a – его бюджет b. Назовем возможным планом потребления участника рынка набор товаров, суммарная стоимость которых не превосходит его бюджета. Сопоставим каждому участнику рынка a множество возможных планов потребления. Этим определяется соответствие R из A в множество всех подмножеств множества Т. Например, пусть T={t₀, t₁, t₂, t₃}, p₀=–2, p₁=1, p₂=2, p₃=3 (отрицательную цену имеет товар, который может быть продан на рынке, например, труд); A={a₁, a₂, a₃}, b₁=0, b₂=2, b₃=10. Тогда

R(a₁)={{t₀}, {t₀, t₁}, {t₀, t₂}},

R(a₂)={{t₀}, {t₁}, {t₂}, {t₀, t₁}, {t₀, t₂}, {t₀, t₃}, {t₀, t₁, t₂}, {t₀, t₃}},

R(a₃)=2^T

Рассматривая соответствия из X в Y как подмножества множества X×Y, можно говорить о том, что одно соответствие является частью другого, можно образовывать пересечение и объединение соответствий и т. п. Пусть S, R⊂X×Y – пара соответствий из X в Y. Непосредственно из определений вытекают следующие свойства соответствий:

1. 
   1) S⊂R в том и только том случае, если S(x) ⊂R(x) для всех x∈R;
   
2. 
   2) (S∩R)(x)=S(x) ∩R(x);
   
3. 
   3) (S∪R)(x)=S(x) ∪R(x).
   

Пусть R⊂X×Y – соответствие из X в Y.

Соответствие из Y в X, определяемое формулой

R^–1={(y,x)|(x,y)∈R},

называется обратным к соответствию R. Очевидно, x∈ R^–1(y) тогда и только тогда, когда y∈ R(x). Непосредственно из определений следует, что

(R^–1)^–1=R; D(R^–1)= B(R); B(R^–1)=D(R).

Для произвольного множества X обозначим через E_X соответствие, определяющее тождественное отображение множества X в себя, при этом соответствии каждому элементу множества X соответствует лишь сам этот элемент, то есть E_X(x)={x}. Соответствие E_X задается диагональю декартова квадрата множества X:

E_X = {(x,x) | x∈X} ⊂ X×X.

Мы будем называть соответствие E_X тождественным или диагональным.

Например, для бинарного отношения R = {(3,1), (4,1), (4,2)} на множестве А = {1, 2,3,4} графы самого отношения R, обрат­ного отношения R-1, композиций R◦R^-1и R^-1◦R представлены на рис. 3.

R R^-1 R◦R^-1 R^-1◦R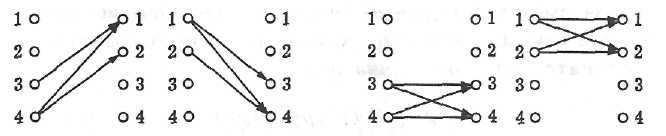



Рис. 3.
Композиция соответствий.

Следуя аналогии с композицией отображений, композицией (произведением) соответствий и называют соответствие

Читается так: множество всех упорядоченных пар (x,y) таких, что существует множество , для которого и .
П р и м е р 4.1.3.

1) Для двух соответствий r₁: АВ иr₂: ВС можно найти их композицию, т.е. сформировать новое соответствие r=(r_1r₂): АС

Например, если А={1;3;5}, В={2;4;6}, С={7;9} и

r₁:АВ имеем R₁={(1;2);(1;4);(3;4);(5;6)}(А×В),

r₂:ВС имеем R₂={(2;9);(4;7);(4;9);(6;7)}(В×С), то

для r:АС имеем R={(1;9);(1;7);(3;7);(3;9);(5;7)}(А×С).
П р и м е р 4.1.4.

Рассмотрим множество программистов {И,П,С}множество компьютерных программ {n₁, n₂, n₃, n₄, n₅} и множество заказчиков программного обеспечения {З₁, З₂, З₃, З₄, З₅}.

Зададим соответствия: R₁ = {(И, n₁), (И,n₃), (И, n₅), (П,n₂), (П,n₄), (С,n₂), (С,n₅)} и

R₂ = {(n₁, З₃), (n₁, З₄), (n₂, З₁), (n₃, З₂), (n₄, З₄), (n₅, З₅)}.

Рассмотрим процесс построения композиции соответствий R₁ и R₂. Начнем с элемента «И». Имеем сечение R₁(И) = {n₁, n₃, n₅}, в свою очередь для каждого элемента множества {n₁, n₃, n₅} имеем следующие сечения соответствия R_{2 :} R₂(n₁) = {З₃,З₄}, R₂(n₃) = {З₂},R₂(n₅) = {З₃}. Отсюда получаем :

(R₁◦R₂)(И) = R₂(n₁) UR₂(n₃)U R₂(n₅) = {З₂,З₃,З₄} – сечение композиции по элементу И. Рассуждая аналогично, получим (R₁◦R₂)(П) = {З₁,З₄} и (R₁◦R₂)(С) = {З₁,З₃}.

Построение графа композиции R₁◦R₂показано на рис. 4.

R₁ R₂ R₁◦R₂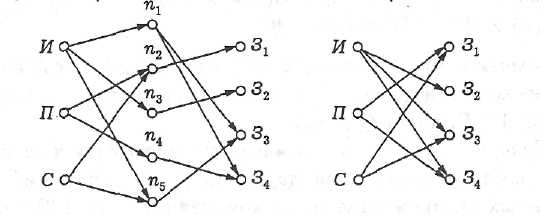


Рис.4. Графическое представление композиции R1◦R2.
Отметим, что область определения композиции соответ­ствий содержится в области определения первого соответ­ствия, а область значений композиции соответствий — в обла­сти значений второго соответствия. Из приведенных рассу­ждений следует, что для того, чтобы композиция соответствий была отлична от пустого соответствия, необходимо и достаточ­но, чтобы пересечение области значений первого соответствия и области определения второго соответствия было не пусто: δ_R1 ∩ ρ_R2 ≠ ∅ .
П р и м е р 4.1.5.

Рассмотрим соответствие



из множества А = {1,2, 3} в множество В = {а, b, d} и соответ­ствие



из множествав множество . В данном

случае но, поскольку , и ∅

П р и м е р 4.1.6.

Пусть T – множество наборов товаров такое же, как в примере из предыдущего пункта. Будем считать, что набор товаров улучшается, если к нему добавляется один из товаров с положительной ценой или из него выводится товар с отрицательной ценой. Будем говорить, что набор товаров V лучше, чем набор товаров U, если V может быть получен из U несколькими последовательными улучшениями. Например, наборы {t₀,t₁}, {t₀,t₁,t₂}, {t₁,t₂} получаются последовательными улучшениям. Обозначим через P(U) множество тех наборов, которые получаются из набора U путем его однократного улучшения. Например, P({t₀,t₁})={{t₀,t₁,t₂}, {t₀,t₁,t₃}, {t₁}}; P({t₁,t₂,t₃})=∅. Тогда P²(U) – это множество наборов, которые получаются из U двумя последовательными улучшениями, P³(U) – это множество наборов, которые получаются из U тремя последовательными улучшениями и т.д. Очевидно, P⁵(U)= ∅ для любого набора U. Положим S=P∪P²∪P³∪P⁴. Тогда S(U) – это множество наборов, которые лучше, чем набор U.

Приведем некоторые свойства композиции соответствий.

Пусть на некотором множестве заданы соответствия ρ, σ и τ. Тогда справедливы следующие тождества:
1)

2) для любого соответствия имеет место

з)

4) для любого бинарного отношения на множестве А имеет место равенство
Эти свойства нетрудно доказать методом двух включений. Рассмотрим в качестве примера доказательство свойства 3. Пусть некоторая упорядоченная пара (х, у)принадлежит ком­позиции. Тогда, согласно формуле для композиции соответствий (см п. 4.1), найдется такой эле­мент z, что и Последнее означает, что или . Таким образом, для элемента zимеем и или и Пер­вая альтернатива имеет место при, а вторая — при , что означает Тем самым включениедоказано.

Доказательство включениязапишем

коротко, используя логическую символику: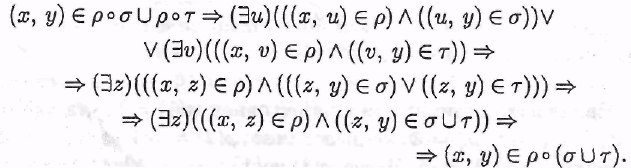



В данном случае доказательства двух включений не совсем симметричны: элементы и и v во второй части доказательства не обязаны совпадать.

Замечание.

В тождестве, выражающем свойство 3, нельзя вместо объединения поставить пересечение, так как в этом случае тождество нарушится. Можно доказать, что сохранится лишь включение



а обратное включение в общем случае не имеет места.

Анализ свойств 2 и 4 показывает, что роль пустого со­ответствуя аналогична роли нуля при умножении чисел, а диагональ множества Л играет роль, аналогичную роли еди­ницы, на множестве всех бинарных отношений на А.

Если— отображение, то оно является соответствием. Обратное к f соответствие из В в A в общем случае не является отображением. Действительно, соответствие, обратное к , состоит из всех упорядоченных пар вида . Поскольку в общем случае могут найтись такие два раз­личных элемента х и х', что, то соответствие в общем случае не будет функционально по второй компоненте и поэтому не будет отображением. Если отображениеинъективно, то обратное соответствие есть частичное отображение из В в А. Если отображениебиективно, то обратное соот­ветствие является отображением из В в А, причем имеют место равенства/