Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов
 Скачать 2 Mb.
|
ПримерМножество чётных целых чисел Eимеет такую же мощность, что и множество целых чисел Z. Определим f : E→Zтак:  . f — биекция, поэтому |E| = |Z|.Ясно, что понятие мощности конечных множеств позволяет сравнивать их по количеству элементов. Так, если A = {1, 3, 5, 7, 9}, а B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4 и потому m (A) > m (B). Однако если мы имеем дело с бесконечными множествами, то пересчитать элементы множества уже не удастся. Но иногда можно, как говорят, установить взаимно однозначное соответствие между двумя бесконечными множествами Множества, между которыми установлено взаимно однозначное соответствие, содержат одинаковое количество элементов. Пример 2 Множество натуральных чисел равномощно множеству нечётных чисел, так как между ними можно установить взаимно однозначное соответствие, например, по следующему правилу:
Так как множество нечётных чисел является подмножеством натуральных чисел, то этот пример показывает, что бесконечное множество может быть равномощно своему подмножеству. Пример 3. Любой отрезок [a; b] равномощен отрезку [0; 1]. Взаимно однозначное соответствие между ними устанавливает формула y = (b − a) · x + a, где  ,  Пример 4. Множества  и  счётны и потому равномощны. В самом деле, установим взаимно однозначное соответствие между ними по следующему правилу:
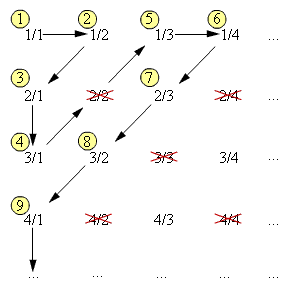
5.2. Счетные множества. “Простейшим” среди бесконечных множеств является множество натуральных чисел. Пересчитывая что-то мы используем целые (положительные) числа 1, 2, 3 ... Их еще называют "натуральными". Мы знаем, что этих чисел нам хватит для пересчета чего угодно. Мы также знаем, что это множество бесконечное. Кантор назвал это множество СЧЕТНЫМ и его мощность - мощностью счетного множества. Мощность этого множества Кантор взял за эталон и стал сравнивать ее с мощностями других множеств. Мощность множества натуральных чисел Nобозначается символом א0(«алеф-нуль»). Множество называется бесконечным, если его мощность ≥ א, таким образом, счётные множества это «самые маленькие» из бесконечных множеств. Следующие кардинальные числа в порядке возрастания обозначаются א1, א2,…. Приведем несколько равнозначных определений счетного множества. Счетное множество — это множество, эквивалентное множеству натуральных чисел. Множество, равномощное множеству всех натуральных чисел, называется счётным множеством. Счетным множеством называется всякое множество, элементам которого можно поставить во взаимно однозначное соответствие множество натуральных чисел. Отсюда, счетное множество - это бесконечное множество, элементы которого перенумеровать натуральными числами, записав их в виде последовательности a1, ..., ап, ... или  Другими словами, счетное множество есть область значений некоторой функции натурального аргумента.Примерами счетных множеств, кроме множества натуральных чисел, являются: - множество целых чисел Z={ 0, -1, 1, -2, 2, -3, 3,...,}.Соответствие между целыми и натуральными числами можно осуществить по схеме n 2n+1 при n 0, n 2|n| при n<0. - множество всех четных положительных (отрицательных) чисел, соответствие по формуле n ↔2n. - множество натуральных степеней числа 2, Множество чисел 2n. Соответствие осуществляется по формуле n 2n. - множество рациональных чисел Q, - множество алгебраических чисел и т.д. - множество положительных рациональных чисел счётно. Действительно, если представить каждое рациональное число в виде несократимой дроби и записать его в следующую таблицу, а затем пронумеровать, как указано на рисунке, то окажется, что множество рациональных положительных чисел действительно счётно.
Мощность счётных множеств есть наименьшая мощность, которую может иметь бесконечное множество. Кантор доказал, что множество всех рациональных и даже всех алгебраических чисел счётно, тогда как множество всех действительных чисел несчётно. Очевидно, что все счетные множества эквивалентны множеству натуральных чисел, а тем самым они все эквивалентны между собой. Кантором было выдвинуто определение бесконечности как такого множества, в котором части и целое могут быть равномощны6, т.е. характеризоваться одним трансфинитным кардинальным числом. Например, мощность счетного множества не изменяется в результате прибавления любого конечного числа элементов. Поскольку каждому конечному или бесконечному множеству соответствует определенная мощность (кардинальное число), то операции над множествами сводятся к действиям над кардинальными числами. Покажем, например, счетность множества алгебраических чисел. Число а называется алгебраическим, если оно является корнем некоторого многочлена с целыми коэффициентами.Так как множество целых чисел счетно, то занумеруем их, например, следующим образом: если целое число n неотрицательно, то поставим ему в соответствие номер 2n+1, если целое число n отрицательное, то поставим ему в соответствие номер 2|n|. Каждому уравнению вида :  (2)поставим в соответствие натуральное число:  , где 2,3,...,p - простые числа, а  - номер целого числа  (коэффициента уравнения (1)), полученного после приведенной нумерации (1).Таким образом можно перенумеровать все уравнения типа (2). Так как каждое уравнение (2) имеет не более n различных корней, то тем самым доказывается счетность множества алгебраических чисел. Таким образом, множество алгебраических чисел (как это было показано ранее) счетно. Свойства счетных множеств. Свойство 1. Всякое подмножество счетного множества конечно или счетно. Действительно, если А - счетное множество, то его элементы можно перенумеровать. Пусть В - подмножество множества А. Тогда, если среди элементов множества В есть элемент с наибольшим номером, то множество В является конечным, в противном случае множество В будет счетным. Свойство 2. Объединение любого конечного или счетного числа счетных множеств, есть счетное множество. Для доказательства этого свойства используется так называемая Канторовская диагональная процедура. Свойство 3. Всякое бесконечное множество содержит счетное подмножество. Действительно, если А - бесконечное множество, то в нем есть хотя бы один элемент а. Внесем его в строящееся подмножество В, присвоив этому элементу номер 1. Так как А - бесконечное множество, то в нем после удаления элемента а, останутся элементы. Возьмем любой элемент, присвоим ему номер 2, удалим его из множества А и включим его в множество В, и т.д. Построенное таким образом множество В будет счетным. 5.3. Континуум. Мощность континуума. Кантор доказал, что если взять бесконечное множества счетной мощности, например, множество целых положительных чисел и построить (разумеется, умозрительно) множество, содержащее в качестве элементов все подмножества этого множества, то получим мощность БОЛЬШУЮ, чем счетная мощность. В принципе не существует способа пересчитать (пусть в бесконечности) такое множество. В нем всегда больше элементов. Эта новая бОльшая мощность называется мощностью КОНТИНУУМА. Континуум (от лат. Слова continuum – непрерывное) теории множеств — кардинал или класс множеств, равномощных множеству вещественных чисел. Например, совокупность всех точек отрезка на прямой или множество всех иррациональных чисел. Говорят: «множество мощности континуум» или «континуальное множество». Бесконечное множество, не являющееся счетным, называется несчетным. Теорема 1 Кантора о существовании несчетных множеств. Множество действительных чисел, заключенных между нулем и единицей, несчетно. Доказательство. Пусть все действительные числа, заключенные в интервале от нуля до единицы, можно перенумеровать. Представим каждое такое действительное число в виде бесконечной десятичной дроби (дополнив, если это необходимо, их нулями). Покажем, что существует такое действительное число из интервала от нуля до единицы, которого нет среди перенумерованных чисел. Это число строится так:  , где десятичный знак этого числа отличен от десятичного знака первого перенумерованного числа, сотый знак - отличается от сотого знака второго перенумерованного числа и т.д. Полученное противоречие и доказывает теорему.
Множеству всех действительных чисел равномощны:
Про множества, эквивалентные множеству действительных чисел отрезка [0,1], говорят, что они имеют мощность континуума. Эта мощность обозначается c или א1. Приведем примеры несчетных множеств. Пример 12.
Итак, самыми “маленьким” из бесконечных множеств являются счетные множества. Более высокий “порядок” у бесконечных множеств составляют множества мощности континуум. Континуум – не самая большая из бесконечных мощностей. Так, мощность множества всех подмножеств точек числовой оси больше, чем мощность самого множества всех точек оси. Она обозначается 2c и называется гиперконтинуумом. На вопрос о существовании множеств более высокого порядка, чем континуум отвечает следующая теорема, так же принадлежащая Кантору. Теорема 2 Кантора о существовании множеств мощности более континуума. Пусть M - некоторое множество и B(M) - булеан множества M. Тогда |B(M)|>|M|. Доказательство Если множество M - конечно и |M|=n, то теорема верна, т.к. |P(M)|=  >n.Очевидно, что для бесконечного множества M выполняется |P(M)|  |M|, так как множество P(M) содержит по крайней мере все одноэлементные подмножества из элементов множества M. Покажем что |P(M)|  |M|. Доказательство будем проводить от противного.Пусть |M|=|P(M)|, т.е. множества M и P(M) эквивалентны, а это означает, что между элементами этих множеств можно установить взаимно однозначное соответствие. Установим такое соответствие: Элементу a из множества M поставим во взаимно однозначное соответствие множество A - элементы булеана P(M); элементу в поставим во взаимно однозначное соответствие множество В (элемент множества (M)); элементу с - множество С и т.д. Постоим следующее множество X элементов из M: для пары соответствующих членов (а,А) элемент а мы поместим в множество X тогда и только тогда, если элемент а не принадлежит множеству А, и элемент а мы не поместим в множество X , если а принадлежит множеству А; алогично, элемент в помещаем в множество X , если этот элемент не принадлежит множеству В и не помещаем в множество X , если этот элемент принадлежит множеству В; так по всем элементам множества A. Так как множество X будет состоять из элементов множества M, то это множество является элементом булеана множества M и ему, как и любому другому элементу из множества P(M), должен взаимно однозначно соответствовать некоторый элемент x из множества M. Покажем, что этого не может быть. Действительно, если элемент x принадлежит соответствующему ему множеству X, то этот элемент мы в множество X включить не должны, если же элемент x не принадлежит множеству X, то мы должны этот элемент включить в множество X. Полученное противоречие доказывает теорему. Теорема Кантора - Бернштейна. Пусть даны два произвольных множества A и B. Если можно установить взаимно-однозначное соответствие, между множеством A и некоторым подмножеством множества B и, наоборот, между множеством B и некоторым подмножеством множества A, то множества A и B - равномощны. Доказательство существования иррациональных и трансцендентных чисел. Классификация чисел: Действительные или вещественные числа (R) включают в себя рациональные (разумные) и иррациональные числа. Рациональные (Q) - это десятичные периодические дроби, представимые в виде p\q, q>0, p и q - целые числа. Иррациональные (J), это десятичные непериодические дроби, например, e,  , и т.д. |
1