Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов
 Скачать 2 Mb. Скачать 2 Mb.
|
|
П р и м е р на дополнение множества: Пусть С = {(x,y): x2 + y2 ≤ 1} – множество точек плоскости, находящихся в круге радиуса 1, тогда 2.2. Диаграммы Венна. Свойства операций над множествами. Наглядно операции над множествами можно проиллюстрировать с помощью диаграмм Эйлера – Венна. Сами множества представлены кругами, а результаты операций выделены штриховкой. 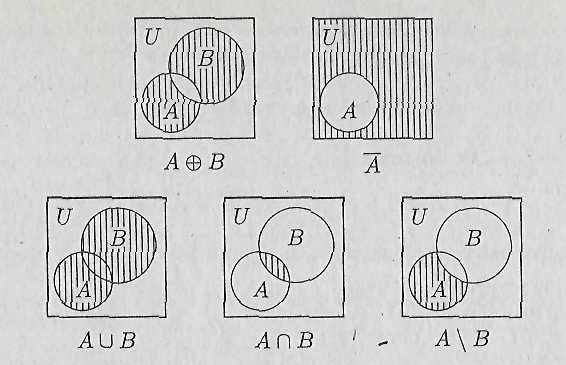 Рис. 1. Графическое изображение алгебраических операций над множествами А и В. Введенные нами ранее операции над множествами обладают следующими свойствами:  11. А\В=А 12. 13. 14. 15. Любое из этих тождеств может быть доказано методом двух включений. Докажем, например, тождество 11. Сначала установим , что А\В=А В качестве другого примера докажем тождество 12. Пусть 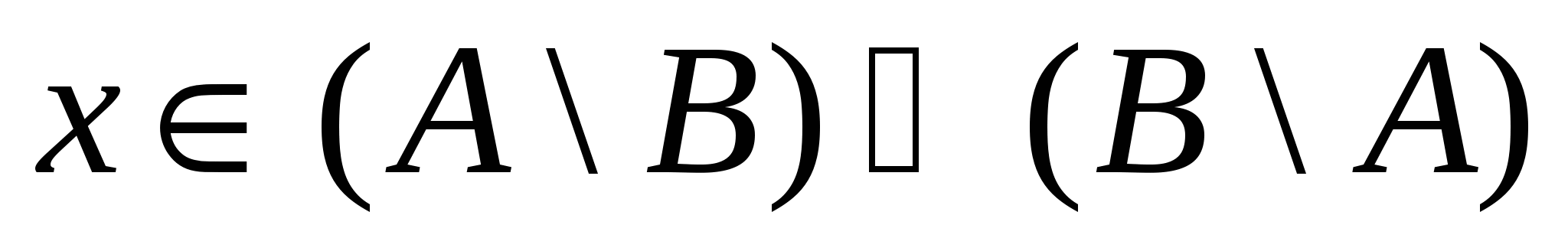 . Это означает, что . Это означает, что или 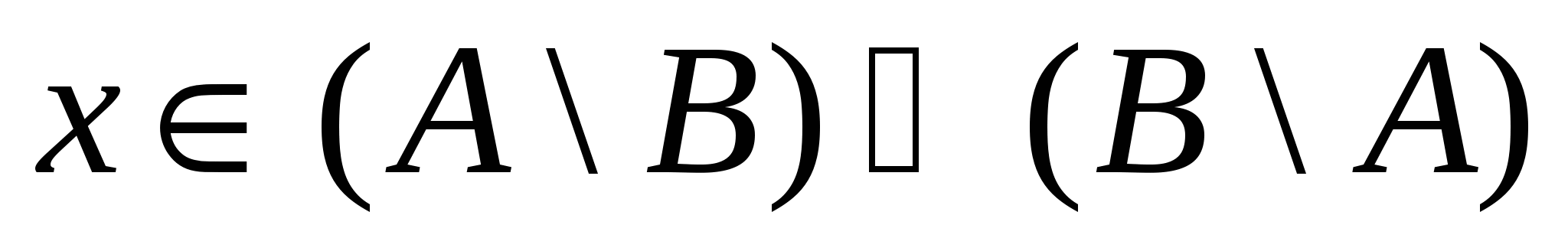 следует следует Покажем теперь обратное включение Пусть Оба включения имеют место, и тождество 12 доказано. Метод двух включений является универсальным и наиболее часто применяемым методом доказательства таких тождеств. Кроме того эти тождества можно доказывать, используя ранее доказанные тождества для преобразования левой части к правой или наоборот. Такой метод доказательства часто называют методом эквивалентных преобразований. Докажем методом эквивалентных преобразований тождество 15, пользуясь тождествами 1-12. Преобразуем левую часть к правой: Тождество доказано.
Пусть А и В произвольные множества. Неупорядоченная пара на множествах А и В – это любое множество {a,b}, где Упорядоченная пара на множествах А, В обозначается как (a,b) и определяется не только самими элементами Простейший и важнейший пример упорядоченной пары дает аналитическая геометрия. Если на плоскости введена некоторая прямоугольная система координат, то каждая точка плоскости однозначно задается упорядоченной парой действительных чисел – координатами этой точки. (Точка, заданная координатами (1,3), совсем не то же самое, что точка с координатами (3,1). Обобщением понятия упорядоченной пары является упорядоченный n-набор, или кортеж. В отличие от конечного множества {a1,a2,…,an} кортеж (a1,a2,…,an) на множествах А1,А2,…,Аn характеризуется не только входящими в него элементами Определение. Два кортежа (a1,a2,…,an) и (b1,b2,…,bn)на множествах А1,А2,…,Аn равны, тогда и только тогда, когда a1=b1, a2=b2,…, an=bn. Последнюю систему равенств более коротко принято записывать так ai=bi, i= Проекцией кортежа на i-ую компоненту называется его i-ая компонента, что принято обозначать так: Прi(x1;x2;...;xn)=(xi) Проекцией кортежа на i-ую, j-ую,m-ую компоненты называется кортеж, компоненты которого принимают значения i-ой, j-ой,m-ой компонент исходного кортежа, что принято обозначать так: Прi;j;...m (x1;x2;...xi;...xj;...xm;...xn)=(xi;xj;...xm). Определение. Декартовым (прямым) произведением множеств А и В и называется множество всех упорядоченных пар (a,b) таких, что В частности, если А=В то обе координаты принадлежат множеству А и такое произведение обозначается А2. П р и м е р. Пусть A={1,2,3} и B={2,3,4}. Тогда множество A×B состоит из следующих девяти элементов: (1,4), (2,4), (3,4), (1,3), (2,3), (3,3), (1,2), (2,2), (3,2). Графически элементы произведения множеств A.B удобно помещать на «координатной плоскости», считая, что первый множитель A расположен на горизонтальной полуоси, а второй множитель B – на вертикальной. Например, (1,4) (2,4) (3,4) (1,3) (2,3) (3,3) (1,2) (2,2) (3,2) Аналогично, можно дать определение декартова произведения множеств А1,А2,…,Аn. Определение. Декартовым произведением множеств А1,А2,…,Аn называется множество всех упорядоченных наборов (кортежей) (a1,a2,…,an) длины nтаких, что Если же все множества Аi, i = Заданное множество кортежей всегда является подмножеством прямого произведения множеств, т.е. {(a1; a2;...; an)| a1A1, a2A2, ...,anAn}(A1×A2×...×An). По определению полагают, что первая декартова степень любого множества А есть само множество А, т.е. А1 = А. Т е о р е м а 1. Пусть Доказательство. Для доказательства применим метод математической индукции. Для п = \ теорема верна. Предположим, что теорема верна для п= k. Докажем, что утверждение теоремы справедливо для п = k+1. По предположению Припишем справа к нему элемент ak+1из Ak+1. Это можно сделать тk+1разными способами. При этом получится mk+1 различных наборов из A1 х А2х... х Ak+1. Таким образом, из всех Таким образом, |А1×А2×…×Аn|=m1m2...mn, что определяет максимальное число кортежей. Следствие. При обработке данных на компьютере прямое произведение множеств широко используют в формировании составных типов данных. Например, на алгоритмическом языке Фортран предложение INTEGER*2VECT(10) описывает составное данное (кортеж) с именем VECT, содержащим 10 компонент типа INTEGER, причем для каждой компоненты в памяти выделено поле размером 2 байта. В базах данных такой кортеж называют записью(record). Свойства декартова произведения : 1) 2) 3) Эти свойства нетрудно доказать методом двух включений. Докажем, например, первое тождество. Если Доказательство обратного включения аналогично. Обратим теперь внимание на третье тождество. Из него вытекает, что пустое множество при построении декартовых произведений множеств играет ту же роль, что и нуль при умножении чисел. Докажем справедливость этого тождества. В самом деле, множество ∅ |
