|
Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов
Отношения.
Соответствие заданное между элементами одного множества Х, называют отношением.
Таким образом отношение является частным случаем соответствия.
Понятие отношенияслужит в математике для выражения на теоретико-множественном языке связей между объектами.
Например, между объектами математической природы такими отношениями могут быть “быть равным”, “быть большим”, “быть неравным” и т.п.. Все множество отношений между числами может быть {=; ; <; }, а между объектами “нематематической” природы такими отношениями могут быть: “быть родственником”, “быть соседом”, “находиться рядом с ...”, “быть частью” и т.п.
Формальная запись отношения не отличается от записи для соответствий, если принять вместо Y множество Х. Множество пар отношений обозначают символом R. Например,
R={(x1; x2)| x1X, х2 Х} X2- бинарное отношение, или двухместное отношение; Х} X2- бинарное отношение, или двухместное отношение;
Таким образом, бинарное отношение на множестве Х это всякое подмножество декартова произведения Х×Х.
Опираясь на понятие соответствия можно дать еще одно определение бинарного отношения :
О п р е д е л е н и е. Всякое соответствие 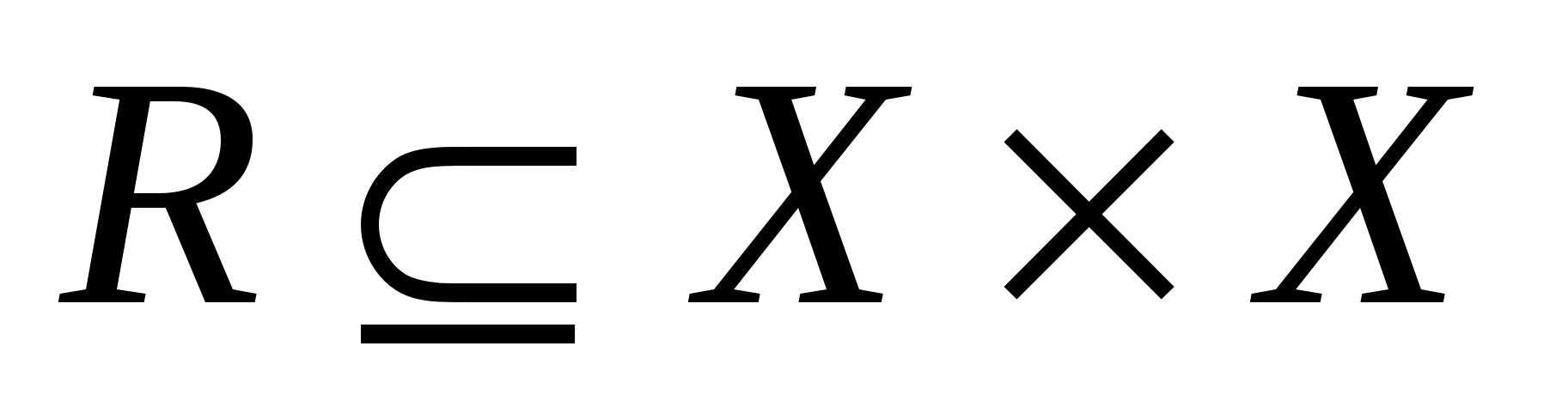 из множества Х в себя, т.е. подмножество множества Х2, называется бинарным отношением на множестве Х. из множества Х в себя, т.е. подмножество множества Х2, называется бинарным отношением на множестве Х.
Т.к.бинарное отношение на множестве Х - это всякое подмножество декартова произведения Х×Х, то для бинарных отношений на множестве X определены булевы операции (объединение, пересечение и др.).
О п р е д е л е н и е. Бинарное отношение на множестве Х, состоящее из всех пар (х,х), т,е, пар с совпадающими компонентами, называют диагональю множества Х и обозначают idХ.
Нетрудно понять, что диагональ Х есть тождественное отображение Х на себя.
Подмножество R⊂Xn называется n-местным или n-арным отношением на множестве X.
При n=1 отношение называется унарным. Унарное отношение на множестве X – это просто некоторое подмножество R множества X. Унарное отношение можно трактовать как свойство: элемент x∈X обладает свойством R, если x∈R.
Наиболее часто в приложениях используются двухместные, или бинарные отношения, которые в основном и будут изучаться в дальнейшем.
Правила отношений также удобно представить в операторной форме:
r:XX или r: XnX.
Способы задания бинарного отношения.
Отношения можно задавать перечислением всех его элементов, т.е. формированием списков. Так {(1,1),(1,2),(2,2),(3,4)} – пример задания бинарного отношения на множестве А = {1,2,3,4} с помощью списка.
Задание отношения с помощью предикатов. Например, на множестве целых чисел можно задать предикат Р1(х):“х – четное число”. Префикс «1» указывает на то, что предикат формирует унарное отношение. В результате будет сформировано множество R(x)={2;4;6;8;...}, являющееся унарным отношением. Можно привести задания бинарных отношений. Например, на множестве целых чисел Z опираясь на вычисление предикатов Р12(x1; x2):-” x1 >x2”, Р22(x1; x2):-” x1 =x2”, Р32(x1; x2):-” x1 < x2”, Р42(x1; x2):”x1 и х2 имеют общий делитель” будут, соответственно сформированы следующие подмножества:
R1(x1; x2)={(10;6);(8;5);(3;1);...} Z×Z;
R2(x1; x2)={(10;10);(8;8);(5;5);(3;3);...} Z×Z;
R3(x1; x2)={(6;10);(5;8);(3;5);(1;3);...} Z×Z;
R4(x1; x2)={(10;2);(10;5);(8;4);(6;3);...} Z×Z.
3) С помощью матриц. При матричном описании бинарного отношения удобно воспользоваться квадратной матрицей (Х×Х), строки и столбцы которой есть элементы множества Х, а на пересечении i-ой строки и j-го столбца ставят знак “1”, если предикат Р2(xi; xj)=“истина” и знак “0”, если предикат Р2(xi; xj)=”ложь”, т.е.
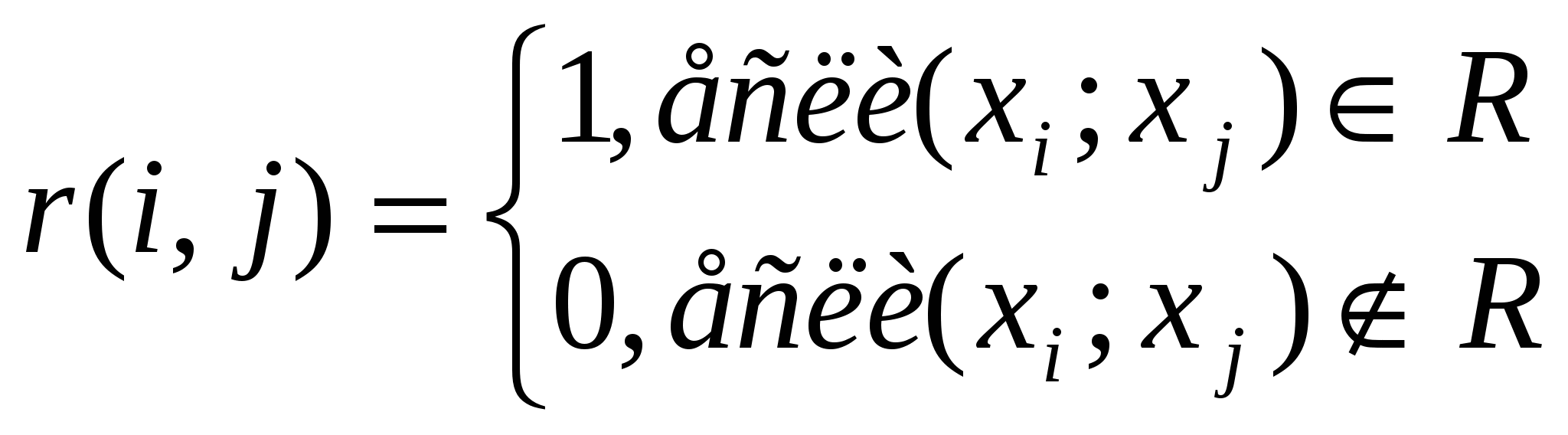
Например, для множества целых чисел Z и предиката P4(x1;x2):-” имеют общий делитель”, заданном на множестве целых чисел матрица выделена в таблице 2 прямоугольными скобками [ ].
Т а б л и ц а 2.
    r4 r4
|
2
|
3
|
4
|
5
|
6
|
8
|
10
|
2
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
3
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
4
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
5
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
6
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
8
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
  10 10
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
5).
П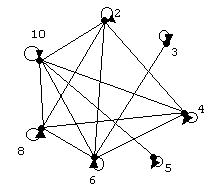 ри графическом представлении отношения все элементы множества Х изображаются точками на плоскости листа и называются вершинами графа, а отношения между i-ым и j-ым элементами множества Х-линиями, которые называют ребрами ( или дугами) графа. В целом фигура, полученная на плоскости листа, называется графом. На рис.5 представлен граф для заданного множества целых чисел и отношения R4(xi;xj) ⊆Z. ри графическом представлении отношения все элементы множества Х изображаются точками на плоскости листа и называются вершинами графа, а отношения между i-ым и j-ым элементами множества Х-линиями, которые называют ребрами ( или дугами) графа. В целом фигура, полученная на плоскости листа, называется графом. На рис.5 представлен граф для заданного множества целых чисел и отношения R4(xi;xj) ⊆Z.
Рис. 5. Граф отношения R4(xi;xj) на Х={2;3;4;5;6;8;10}.
6) Для наглядного изображения соответствий из А в В и, в частности бинарных отношений используется также способ, состоящий в интерпретации отношения как подмножества декартова произведения, которое можно изображать примерно так же, как на плоскости можно изображать подмножества декартова квадрата числовых множеств. Например, множество точек окружности x2 + y2 = 1 есть график бинарного отношения на множестве действительных чисел, состоящего из всех таких упорядоченных пар (х,y), что 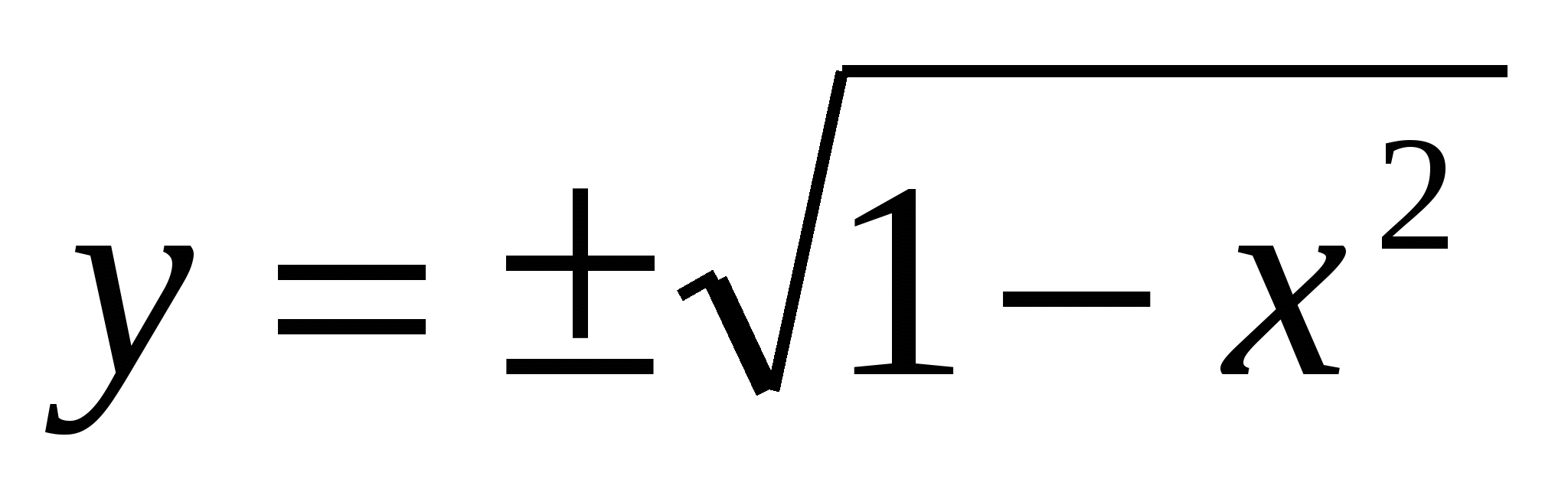 , или, что равносильно, компоненты пар удовлетворяют уравнению x2 + y2 = 1. Область определения этого бинарного отношения есть отрезок [-1,1], область значений – также отрезок [-1,1]. , или, что равносильно, компоненты пар удовлетворяют уравнению x2 + y2 = 1. Область определения этого бинарного отношения есть отрезок [-1,1], область значений – также отрезок [-1,1].
Простейшим примером бинарного отношения является отношение нестрогого неравенства (например, 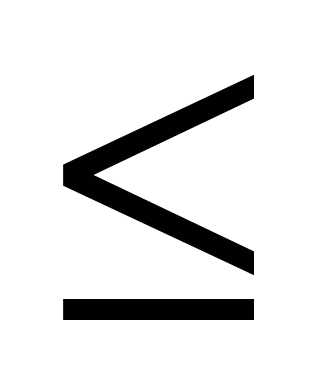 ) на множестве действительных чисел R. Здесь каждому ) на множестве действительных чисел R. Здесь каждому 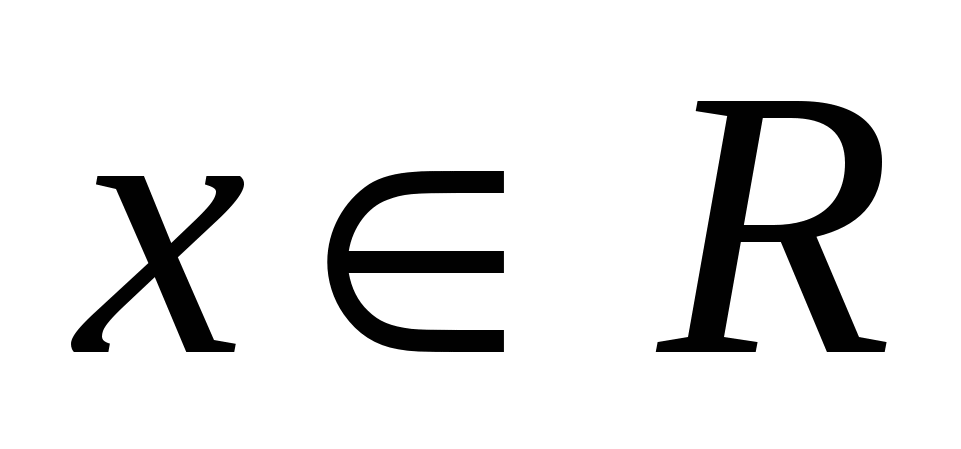 поставлены в соответствие такие поставлены в соответствие такие 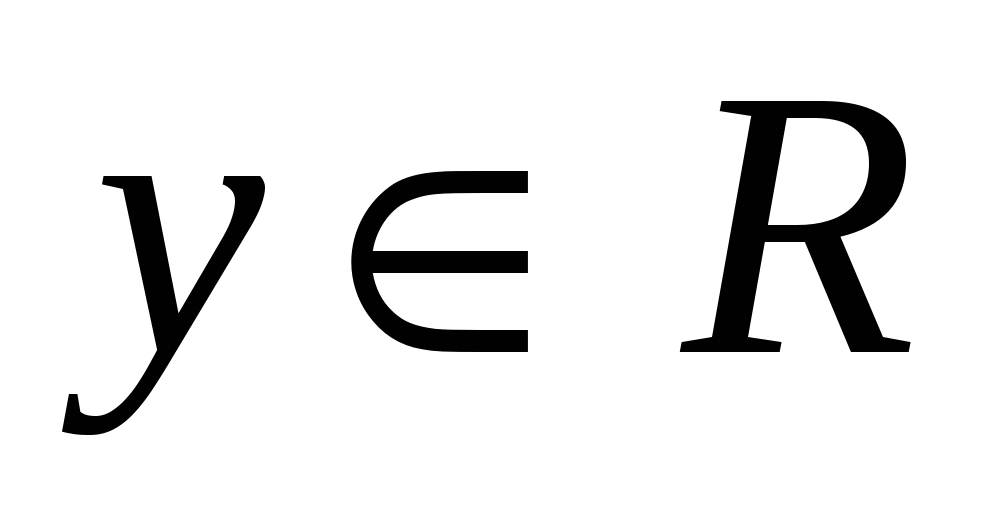 , для которых справедливо , для которых справедливо 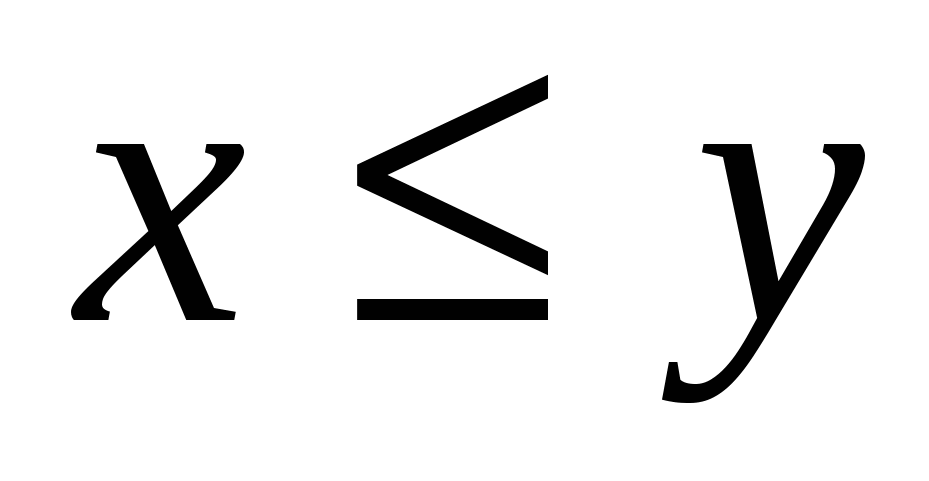 . .
П р и м е р ы .
1) Пусть А= В = N . Рассмотрим отношение “<”, тогда множество натуральных чисел, задаваемых этим отношением можно записать как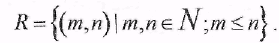 Это отношение выполняется, например, для пар (5, 7), (2, 2), но не выполняется для пары (5,4). Это отношение выполняется, например, для пар (5, 7), (2, 2), но не выполняется для пары (5,4).
2) Пусть A = B = N. Отношение «иметь общий делитель, отличный от единицы» выполняется для пар (2,4), (З,15), но не выполняется, например, для любой пары (n, n +1).
Если (x1; x2) R, то говорят, что элементы x1 и x2 находятся в отношении R. Часто этот факт записывают следующим образом х1Rх2, говоря при этом об элементах, связанных бинарным отношением R. Так, пишут 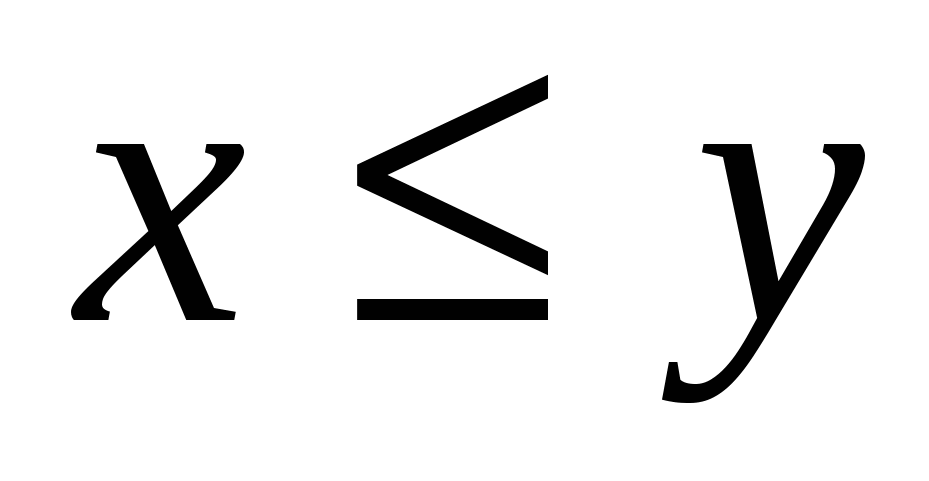 , а не , а не 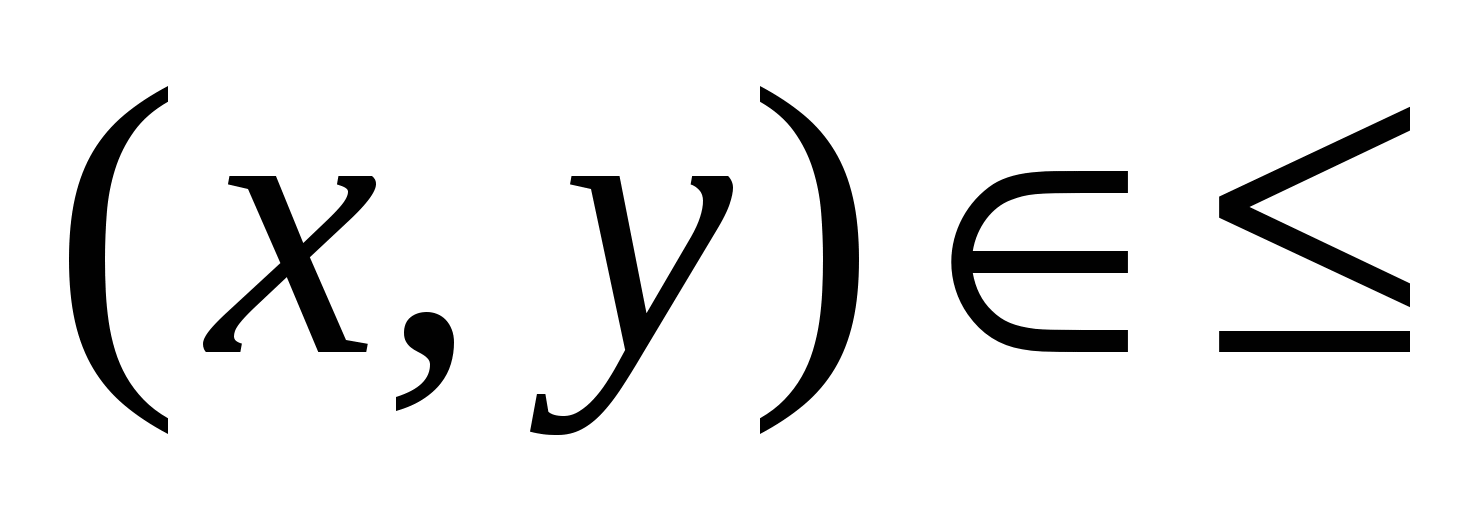 . .
В приложениях двухместные, или бинарные отношения используются наиболее часто.
Приведем теперь несколько важных определений относящихся к бинарным отношениям.
Областью определения бинарного отношения Rназывается множество
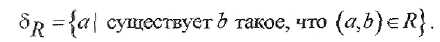
П р и м е р ы.
1) Пусть 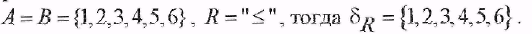
2) Пусть 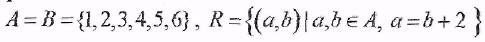 , тогда , тогда 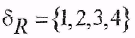
Областью значений бинарного отношения Rназывается множество
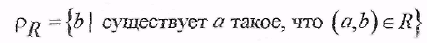
П р и м е р ы.
1) Пусть 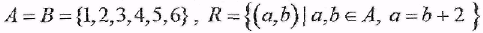 , тогда , тогда 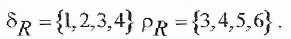
2) Пусть 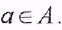 Множество Множество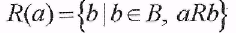 называется образом элемента а в В. называется образом элемента а в В.
3) Пусть 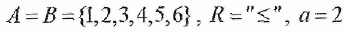 , тогда , тогда 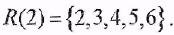
Обратным отношением для бинарного отношения Rназывается бинарное отношение
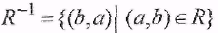
П р и м е р ы.
1) 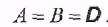 Обратным для Обратным для 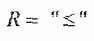 является является 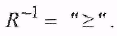
2) 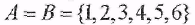 . Обратным для отношения двух чисел «иметь общий делитель ≠ 1» будет оно само. . Обратным для отношения двух чисел «иметь общий делитель ≠ 1» будет оно само.
Пусть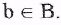 Множество Множество 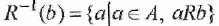 называется прообразом элемента bв А. называется прообразом элемента bв А.
П р и м е р.
Пусть 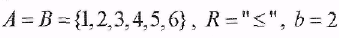 , тогда , тогда 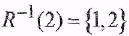
Пусть 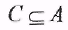 . Образом множества С относительно бинарного отношения Rназывается объединение образов всех элементов С . Образом множества С относительно бинарного отношения Rназывается объединение образов всех элементов С
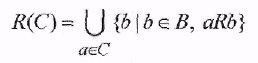
П р и м е р.
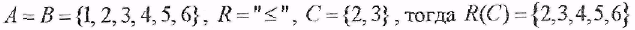
Если 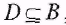 , то прообразом множества относительно Rназывается объединение прообразов всех элементов D , то прообразом множества относительно Rназывается объединение прообразов всех элементов D
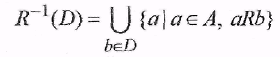
П р и м е р
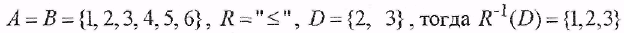
Пусть R - бинарное отношение на А х В . Если 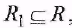 , то R1 называется сужением R. , то R1 называется сужением R.
Дополнением бинарного отношения R между элементами А и В является множество 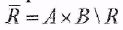
П р и м е р
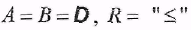 . Дополнением является . Дополнением является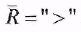
Для двух бинарных отношений 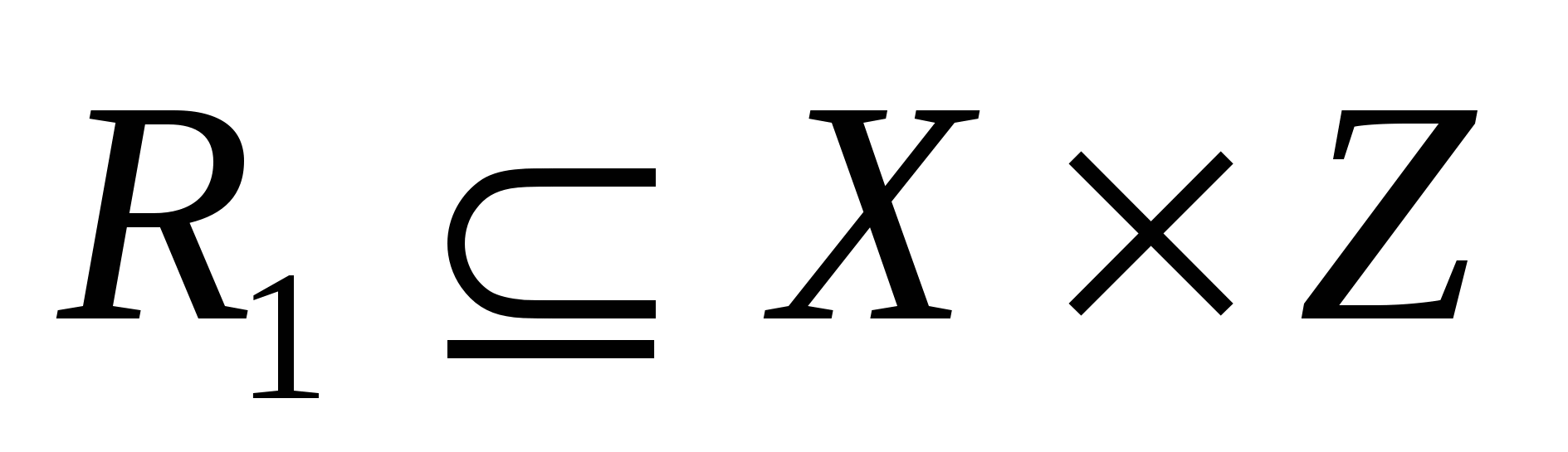 и и 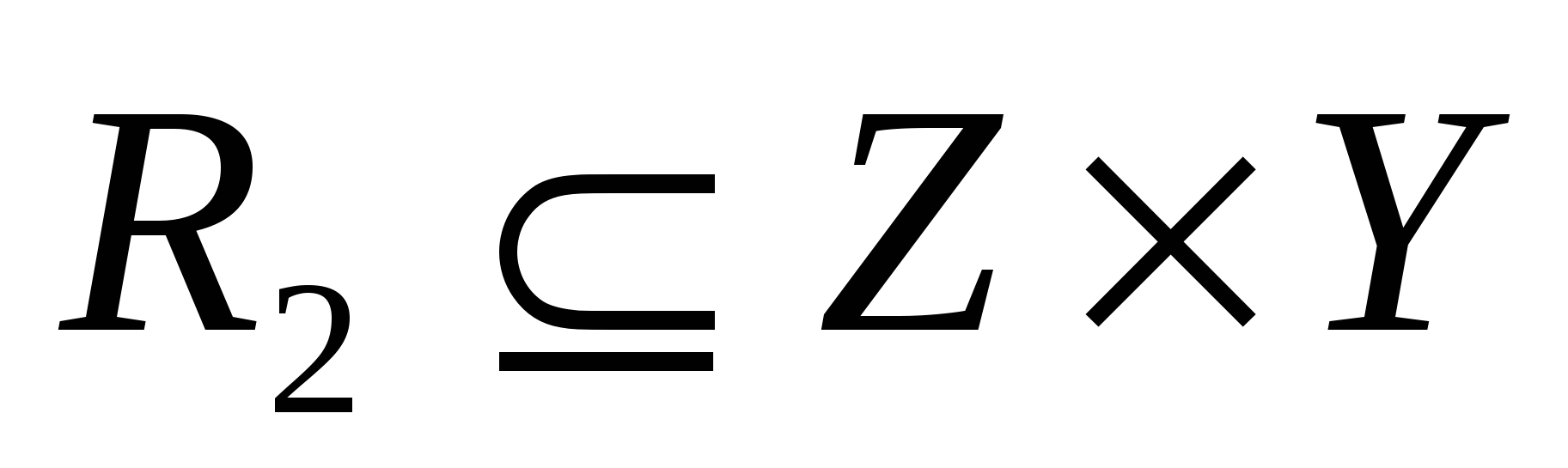 , заданных на множестве А их композиция , заданных на множестве А их композиция
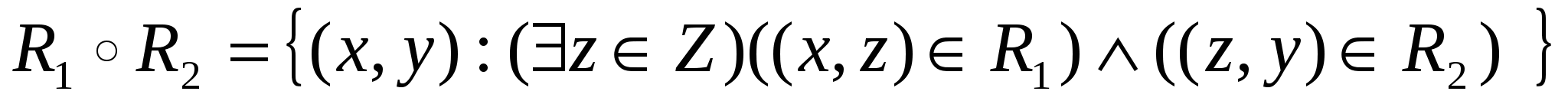
как соответствий является бинарным отношением на том же множестве А.
П р и м е р.
Пусть на множестве А ={1.2.3.4 } заданы бинарные отношения
R1 = {(x,y) : x+ 1 < y} и R2 = {(x,y) : | x– 1 | = 2 }.
Найдем композицию R1 ◦ R2.
Для x = 1 имеем сечение отношенияR1 : R1 (1) = {3,4}. R2 (3) = {1}, R2 (4) = {2} и (R1 ◦ R2)(1) =
= R2 (3) UR2 (4) = {1,2}
Для x = 2 имеем сечение R1 (1) = {4} . R2 (4) = {2} и (R1 ◦ R2)(2) = {2}
Для x = 3 и x = 4 R1 (3) =R1 (4) = ∅, то в итоге получим R1 ◦ R2 = {(1,1), (1,2), (2,2)}.
Построение полученной композиции проиллюстрировано на рис. 6.
R1 R2 R1 ◦ R2
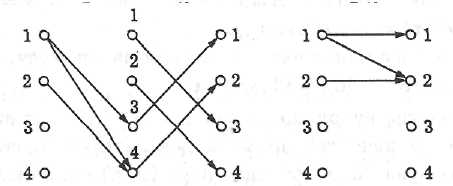
Рис. 6. Графическое изображение прямой композиции отношений.
Найдем теперь композицию R2 ◦ R1.
Поскольку R2 (1) = {3} , а R1 (3) = ∅, то (R2 ◦ R1)(1) = ∅. Аналогично R2 (2) = {4}, а R1 (4) = ∅,
Поэтому (R2 ◦ R1)(2) = ∅. Далее R2 (3) = {1}, R1 (1) = {3,4}, поэтому (R2 ◦ R1)(3) = {3,4}.
ЗатемR2 (4) = {2}, R1 (2) = {4} и (R2 ◦ R1)(4) = {4}. В итоге получим R2 ◦ R1 = {(3,3), (3,4), (4,4}.
Графическое изображение этого результата приведено на рис. 7.
R2 R2 R2 ◦ R1
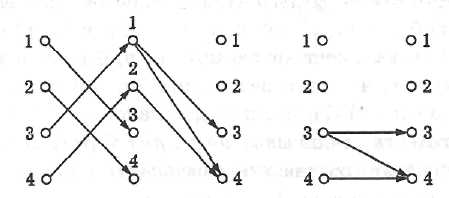
Рис. 7. Графическое изображение обратной композиции отношений.
Легко видеть, что R1 ◦ R2 ≠R1 ◦ R2.
Композицию R ◦ R бинарного отношения Rна некотором множестве с самим собой называют квадратом бинарного отношения R и обозначают R2.
П р и м е р.
Пусть отношение R на множестве действительных чисел определено как функция y = ax+ b. Найдем квадрат этого отношения (линейной функции от одного переменного).
Согласно формуле для графика композиции отображений
f1f2 = 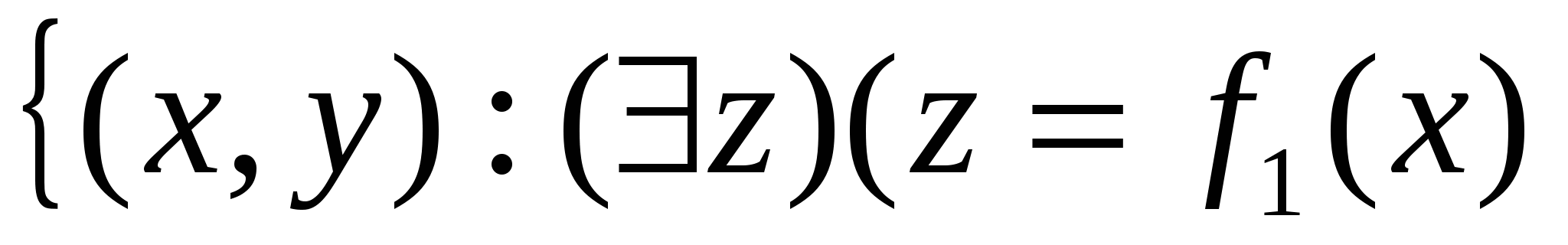 и и 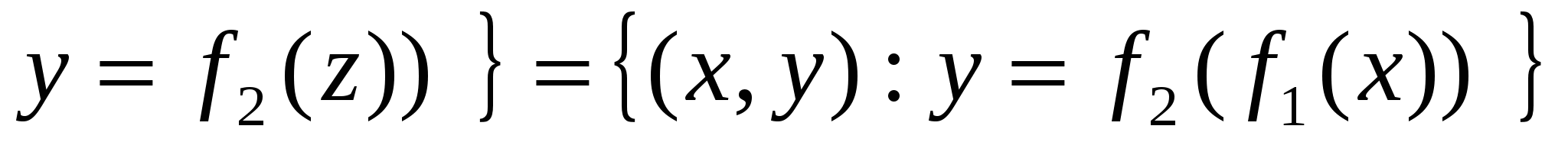 (см. п.3.2) (см. п.3.2)
это будет функция fтакая, что f(x) = a(ax+ b) + c, т.е. f(x) = a2х+ (ab+ c). Это тоже линейная функция, но с другими коэффициентами.
Т е о р е м а . Бинарное отношение ρ на множестве А транзитивно тогда и только тогда, когда его квадрат содержится в нем, т.е. ρ◦ρ ⊆ρ .
Пусть бинарное отношение р на множестве А транзитивно и 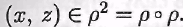 В силу определения композиции бинарных отношений на множестве А существует такой элемент у, что В силу определения композиции бинарных отношений на множестве А существует такой элемент у, что 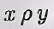 и и 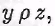 откуда ввиду транзитивности откуда ввиду транзитивности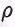 получаем получаем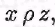 т.е. т.е. 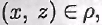 а значит, а значит, 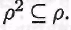
Обратно, пусть бинарное отношение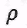 на множестве А таково, что на множестве А таково, что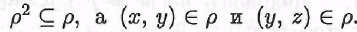 , Тогда в силу определения композиции бинарных отношений на множестве А , Тогда в силу определения композиции бинарных отношений на множестве А 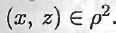 Поскольку Поскольку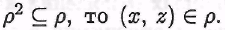 Таким образом, Таким образом,
из того, что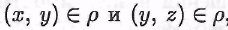 следует, что следует, что 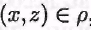 , т.е. бинарное отношение ρ на множестве А транзитивно. , т.е. бинарное отношение ρ на множестве А транзитивно.
Доказанное свойство целесообразно использовать для проверки транзитивности бинарного отношения р на некотором множестве в тех случаях, когда построение квадрата р является более легкой задачей по сравнению с исследованием свойства транзитивности р на основе определения.
Свойства бинарных отношений.
Анализ различных бинарных отношений позволяет выделить наиболее характерные свойства, что необходимо для классификации всего множества отношений. Такими свойствами являются: рефлексивность, симметричность и транзитивность.
Пусть R⊂X×X – бинарное отношение на множестве X (мы будем далее опускать слово «бинарное», когда это не ведет к недоразумениям). Бинарное отношение R на множестве Х называется:
1) рефлексивным, если для любого 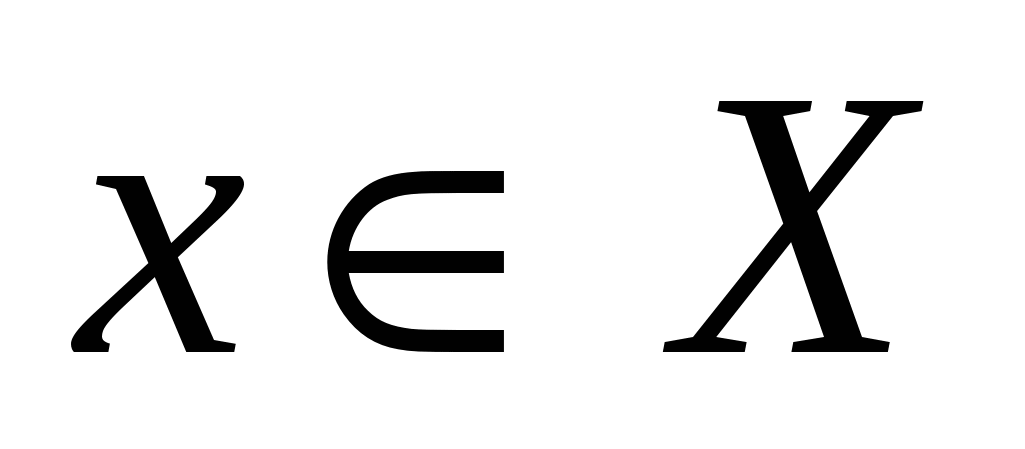 пара пара 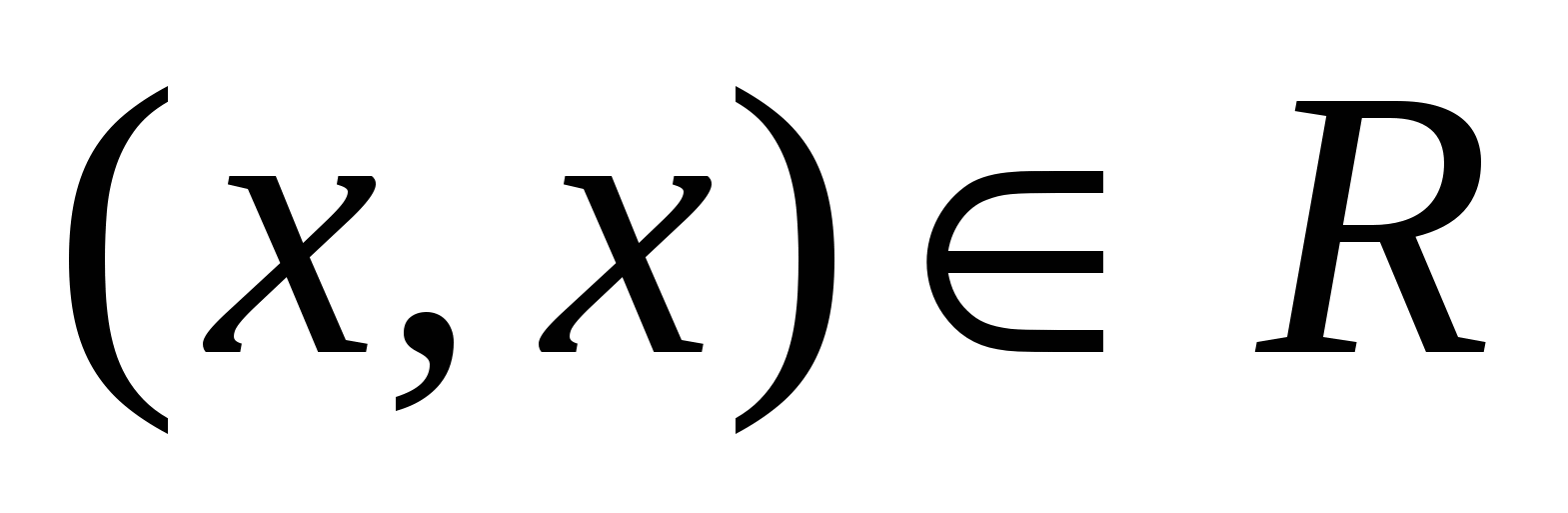 ; ;
2) симметричным, если из того, что 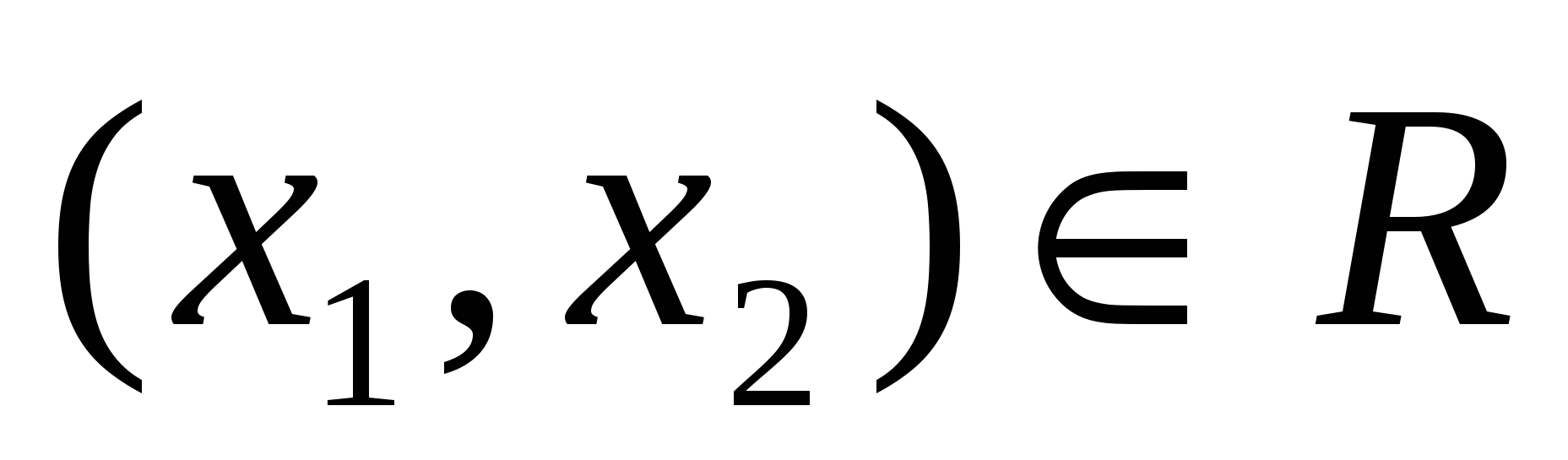 следует, что следует, что 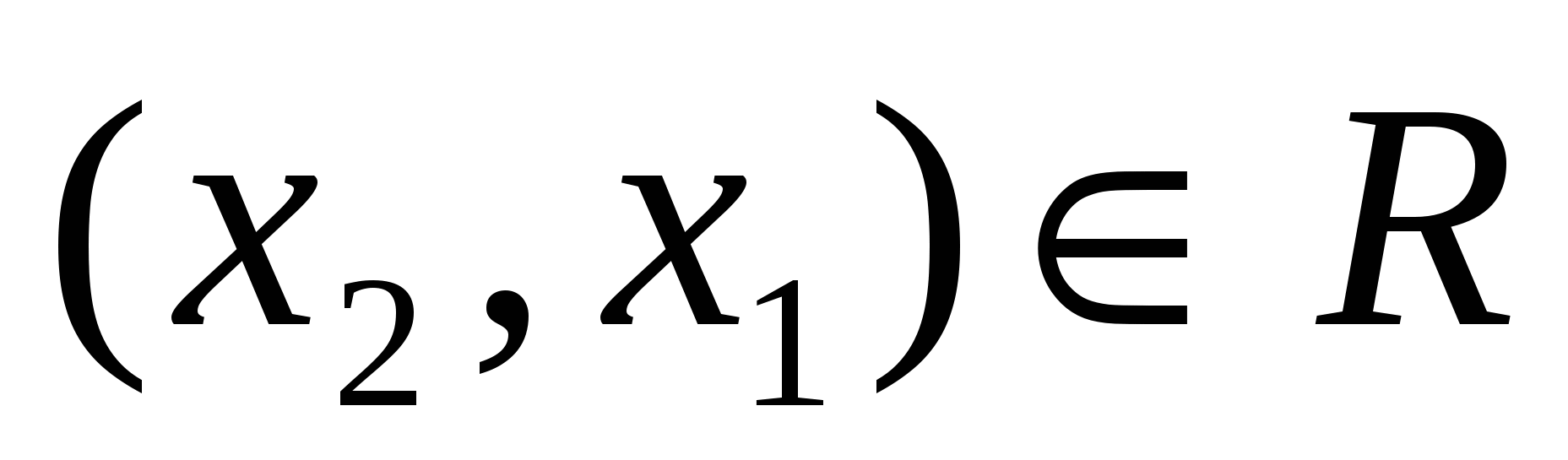 ; ;
3) транзитивным, если из того, что 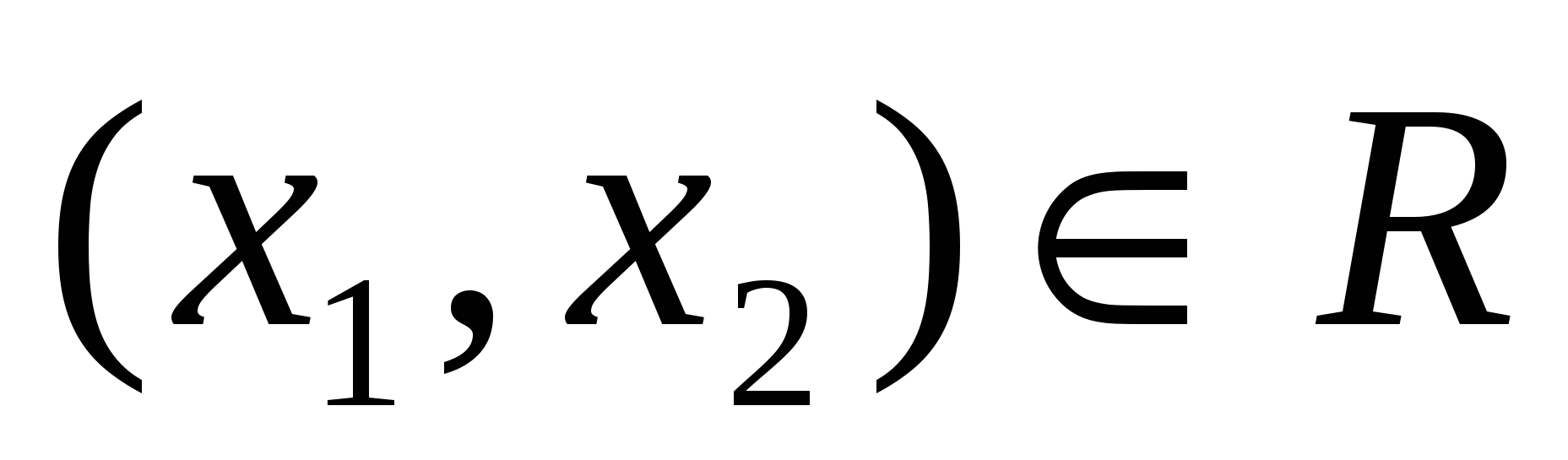 и и 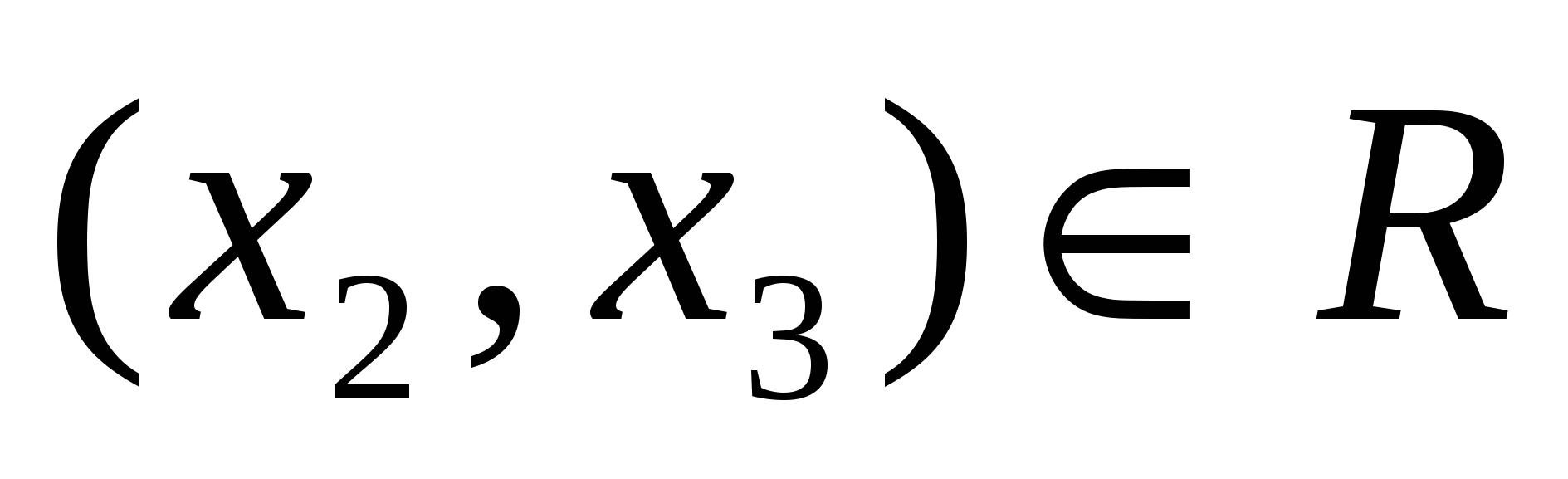 следует следует 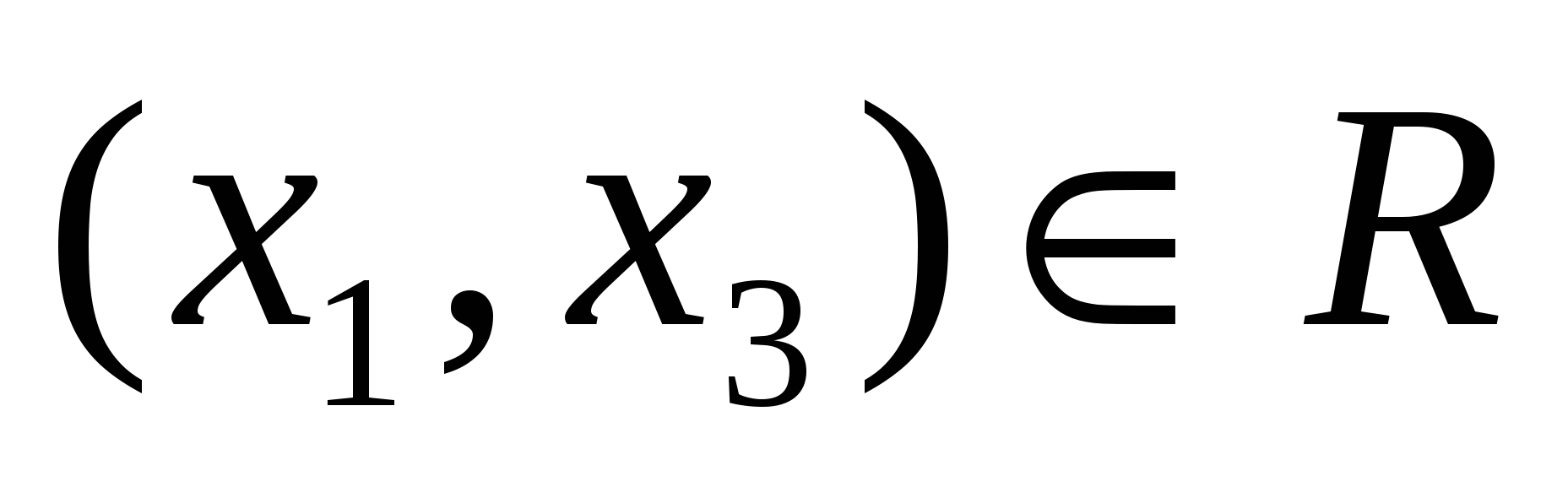 . .
Рассмотрим более подробно каждое свойство.
1) Рефлексивность. Бинарное отношение R рефлексивно если оно содержит все пары вида (x,x), то есть xRx для любого x из X. Рефлексивное отношение на множестве действительных чисел изображается на координатной плоскости множеством точек, содержащим прямую y = x. При матричном задании такого отношения это означает, что на главной диагонали матрицы находятся только “1”, а при графическом представлении - петли при каждой вершине графа (см. рис.8а)).
Бинарные отношения равенства и подобия на множестве геометрических фигур рефлексивны: каждый треугольник равен самому себе и подобен самому себе. На самом деле рефлексивны все отношения равенства: равенство чисел, равенство векторов, равенство множеств и т.п.
Бинарное отношение R называется антирефлексивным, если оно не содержит ни одной пары вида (x,x). Например, отношение x ≤ y рефлексивно, а отношение x < y антирефлексивно. В этом случае для любого хi имеем P(xi; xi)=0, т.е. отношение имеет значение “ложь” применительно к одному элементу хi; такими отношениями являются “быть больше”, “быть меньше”, “быть родителем” и т.п.; при матричном задании такого отношения это означает, что на главной диагонали матрицы находятся только “0”, а при графическом представлении -отсутствие петель при каждой вершине графа (см. рис.8б)).
2) Симметричность. Бинарное отношение симметрично, если вместе с каждой парой (x,y) оно содержит также и пару (y,x), то есть xRy выполняется тогда и только тогда, когда выполняется yRx. Отношение R симметрично, если наличие (или отсутствие) связи между элементами x и y не зависит от порядка, в котором указаны эти элементы. Например, отношение x+y>0 симметрично, а отношение x + 2y>0 – нет (симметричное отношение на множестве действительных чисел изображается на координатной плоскости множеством точек, симметричным относительно прямой y=x). Это могут быть такие отношения: “быть похожим”, “быть эквивалентным”, “быть родственником” и т.п.; Все бинарные отношения в геометрии типа равенства или подобия симметричны. Так, если треугольник АВС подобен треугольнику А'В'С', то и второй из этих треугольников подобен первому.
При матричном задании такого отношения это означает симметричное расположение “1” относительно главной диагонали, при графическом представлении - отсутствие стрелок на линиях, соединяющих вершины xi и xj, или их наличия, но в обе стороны (см. рис.8в)).
Бинарное отношение антисимметрично, если для любой пары (xi;xj) при ij имеем R(xi;xj) R(xj;xi), а при i = j P(xi; xi) =1; такими отношениями являются “быть больше или равным”, “быть меньше или равным” и т.п.; Бинарные отношения неравенства чисел и включения множеств, как строгие, так и не строгие, антисимметричны.
При матричном задании такого отношения это означает несимметричное расположение “1” относительно главной диагонали, но наличие их на главной диагонали, при графическом представлении - наличие стрелок на линиях, соединяющих вершины xi и xj и наличие петель у вершин графа (см. рис.8г)).
Бинарное отношение асимметрично, если невозможно одновременное выполнение условий xRy и yRx. Например, отношение x < y асимметрично. Асимметричность отношения R означает, что R∩R–1= ∅. Отношение R называется антисимметричным, если одновременное выполнение условий xRy и yRx невозможно при x ≠ y, то есть, если xRy и yRx, то x = y. Например, отношение x ≤ y антисимметрично. Ясно, что всякое асимметричное отношение является антисимметричным и антирефлексивным.
Такими отношениями являются “быть больше”, “быть меньше”, “быть родителем” и т.п.; при матричном задании такого отношения это означает только несимметричное расположение “1” относительно главной диагонали и наличие только “0” на ней, а при графическом представлении -наличие стрелок на линиях, соединяющих вершины xi и xj и отсутствие петель у вершин графа (см. рис.8д)).
Следует обратить внимание, что антисимметричное отношение отличается от асимметричного только наличием “1” на главной диагонали или наличием петель у вершин графа.
3) Транзитивность. Бинарное отношение транзитивно, если вместе с любыми парами (x,y) и (y,z) оно содержит также и пару (x,z), то есть из xRy и yRz следует xRz. Например,
а) отношение xx + y > 0 – нет.
б) Пусть М — некоторое множество населенных пунктов. Зададим на нем бинарное отношение достижимости: из пункта А достижим пункт В, если есть дорога, по которой можно доехать из А в В. Это отношение транзитивно, поскольку если из пункта А можно доехать до пункта В, а из В есть дорога до С, то из А можно проехать в С.
в) Бинарные отношения равенства и подобия в геометрии являются транзитивными: если треугольник ABCподобен треугольнику А1В1С1, а этот последний подобен треугольнику А2В2С2, то первый треугольник подобен третьему.
г). Бинарное отношение неравенства на множестве действительных чисел не транзитивно, так как из того, что х≠у и y≠z, вовсе не следует, что х≠z. Аналогично, если х друг у, а у друг z, то — вопреки известной поговорке — это не означает, что х друг z.
Такими отношениями являются “быть больше”, “быть меньше”, “быть родственником” и т.п.; при матричном представлении это означает, что если P(xi; xk)=1 и P(xk; xj)=1, то это же отношение можно установить между вершинами xi и xj через промежуточную вершину xk, т.е. найти P(xi; xj)=1; при графическом представлении -наличие пути из вершины xi в вершину xj через промежуточную вершину xk, используя ребра (xi; xk) и (xk; xj) (см. рис.6е)).
Ниже на рис. 6 приведены матрицы и графы рассмотренных выше отношений.
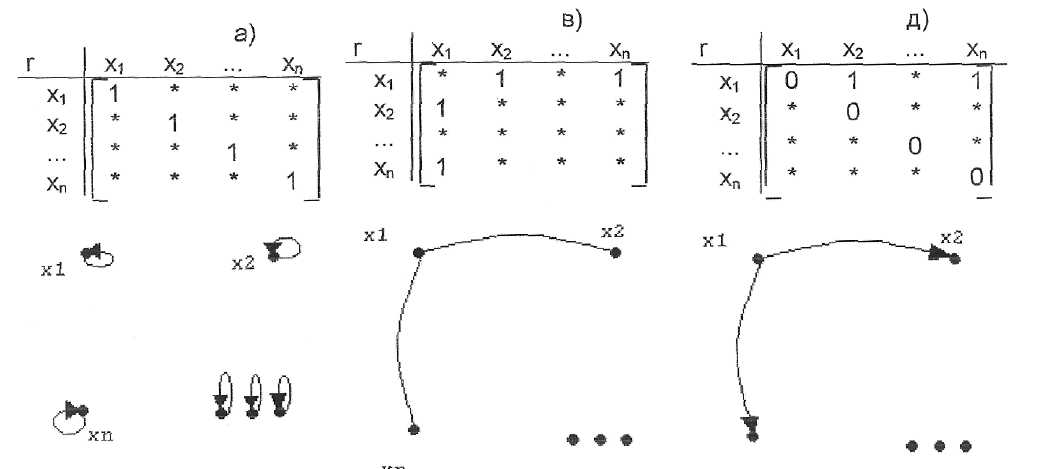
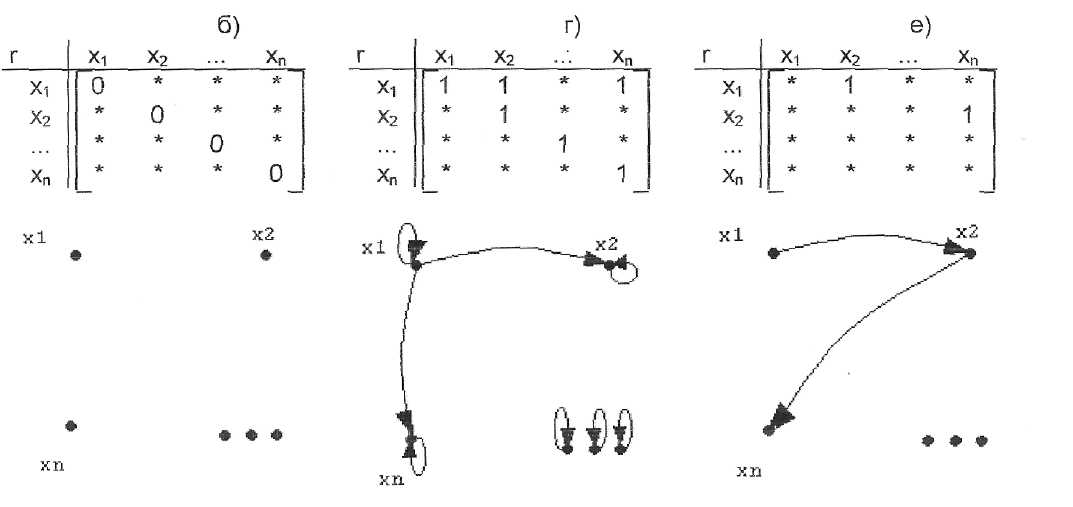
Рис. 8. Матрицы и графы, раскрывающие свойства отношений.
П р и м е р ы.
1) Бинарные отношения равенства и подобия на множестве геометрических фигур рефлексивны: каждый треугольник равен самому себе и подобен самому себе
1) Пусть Х= {1,2,3}, тогда:
а) R1 = {(1,1},(3,3),(1,2)} – транзитивно, но не рефлексивно и не симметрично.
б) R2 = {(1,1),(3,3),(2,2)} - эквивалентность.
в) R3= {(1,2),(2,1)} – симметрично, но не рефлексивно и не транзитивно
г) R4 = {(1,1),(3,3),(1,2),(2,1)} – симметрично, но не рефлексивно и не транзитивно.
д) R5 = {(1,1)}– симметрично и транзитивно, но не рефлексивно.
е) R5 = {(1,2)} – транзитивно, но не не рефлексивно и не симметрично.
Рассмотрим несколько отношений на множестве всех подмножеств некоторого множества U. Отношение включения X⊆Y рефлексивно, антисимметрично и транзитивно. Отношение строго включения X⊂Y, X≠Y, асимметрично и транзитивно.
Пусть R – отношение, которое связывает множества X и Y, имеющие непустое пересечение, X∩Y ≠ ∅. Это отношение симметрично, но, вообще говоря, не транзитивно (транзитивным оно окажется лишь в том случае, когда множество U состоит из одного элемента). Отношение R не рефлексивно; рефлексивным является его сужение на множество непустых подмножеств множества U.
Отношение эквивалентности (
) на множестве Х это бинарное отношение, для которого выполнены следующие условия:
рефлексивность а
а для любого а в Х;
симметричность если ab то ba;
транзитивность если abи bc, то ac.
abчитается как a эквивалентно b.
Контрольные вопросы и задачи.
1. Дано множество Х={x1; x2;...; x6} и Y={y1;y2;..; y4} и элементы прямого произведения этих множеств {(x1; y2);(x2; y1);(x2; y2);(x4; y2);(x4; y4)}. Определите области отправления и прибытия, определения и значений. Что это: соответствие, отображение, отношение?
2. Найти область определения и область значений для отображения:
а) h = {(х; y)|Р(х; y):-”x2+4y2=1”}
б) h = {(х; y)|Р(х; y):-”y 0; y x; x + y 1”}
в) h = {(х; y)|Р(х; y):-”0 x 2; 0 y 1”}
3. Какими свойствами обладают отношения “быть больше”, “быть больше или равным”, “быть родственником”, “быть отцом”?
4. Найти геометрическую интерпретацию следующим выражениям прямого произведения множеств:
а) h = {((a; b); (c; d))| a; b; c; d N};
б) h = {((a; b); (a; b))| a; b N}.
5. Доказать, что если A, B, C и D не пусты, то
а) AC BD, если A B, C D;
б) AC BD, если A=B, C=D;
6. Найти обратное отображение для заданных отображений:
а) h={(х; y)| Р(х; y):-”x делит y и x,y N”};
б) h={(х; y) |Р(х; y):-”2х больше или равно 3y и x,y N”};
7. Найти суперпозицию отношений h = (h1× h2):
h1={(х; z)| Р(х; z):- ”2x 3z и x,zN”};
h2={(z; y)| Р(z; y):- ”2z 3y и z,yN”}.
Для справки
Изоморфизм (от греческих слов √ равный и √ образ, вид, форма) √ это одно из основных понятий современной математики, которое исторически возникло сначала в пределах алгебры в применении к таким алгебраическим системам, как группы, кольца, поля и др., но оказавшееся принципиально существенным для общего понимания строения и структуры самых разных систем.
Автоморфизм (от греческих слов √ сам и ) √ изоморфизм некоторой системы объектов на себя.
Эквивалентность и мощность множеств
Конечные множества 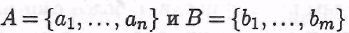 равномощны тогда и только тогда, когда множества А и В состоят из одного и того же числа элементов, т.е. n = m. равномощны тогда и только тогда, когда множества А и В состоят из одного и того же числа элементов, т.е. n = m.
Напомним, что для конечного множества A мы обозначаем через |A| число его элементов и называем это число n мощностью множества A.
В случае бесконечных множеств ситуация оказывается более сложной. Как определить мощность бесконечного множества, если пересчитать количество его элементов невозможно? Первым вопросом, возникшим в применении к бесконечным множествам, был вопрос о возможности их количественного сравнения между собой. Ответ на этот и близкие вопросы дал в конце 70-х гг. 19 в. Г. Кантор, основавший теорию множеств как математическую науку. Следуя Кантору мощность любого, в том числе и бесконечного множества называется кардинальным числом и обозначаем мощность такого множества A через |A|. Таким образом понятие мощности множества становится обобщением, распространяемым на бесконечные множества.
Возможность сравнительной количественной оценки бесконечных множеств опирается на понятие взаимно однозначного соответствия между двумя множествами. Множества A и B называют равномощными, если между их элементами можно установить взаимно однозначное соответствие (ещё говорят: можно установить взаимно однозначное отображение множеств).
Рассмотрим такой пример. Пусть множество (мы намеренно употребляем это слово) людей нужно рассадить в кресла в зале. Мы хотим определить, чего в зале больше: людей или кресел. Можно посчитать всех людей и все кресла и определить, какое из чисел больше. Но можно поступить и иначе: попросить всех сесть! Если останутся свободные кресла, то кресел больше, если же некоторые люди останутся стоять, то больше людей. Наконец, если все люди рассядутся, а свободных кресел не останется, то мы скажем, что людей и кресел поровну.
Аналогично мы можем поступать с множествами. Хотя мы не можем пересчитать все элементы двух бесконечных множеств, но мы можем попытаться поставить их элементы во взаимно-однозначное соответствие, иными словами, рассадить людей в кресла. Если установить такое соответствие удастся, то мы скажем (следуя Кантору), что два рассматриваемых множества равномощны. Если же, как бы мы не устанавливали соответствие, всегда остаются "лишние" элементы из одного из множеств, то это множество имеет большую мощность, чем другое.
При таком определении, оказывается, что множество всех целых чисел равномощно своему подмножеству -- множеству натуральных чисел. Этот парадоксальный, на первый взгляд факт, легко доказать. Выпишем целые числа в таком порядке:
0, 1, --1, 2, --2, 3, --3, ...
Ясно, что так мы выпишем все целые числа. Однако, если теперь мы занумеруем их всех слева направо натуральными числами 1, 2, 3, ..., то все целые числа "рассядутся в кресла" натуральных чисел. Таким образом установлено взаимно-однозначное соответствие между множествами N и Z, и, таким образом, они равномощны. Пока, впрочем, никакого парадокса нет -- просто к бесконечным множествам не всегда применимы наглядные представления.
элементов в этих множествах.
Итак, два множества называются равномощными, если между ними существует биекция. Напомним, что биекция означает взаимно однозначное соответствие
Существование биекции между множествами есть отношение эквивалентности, а мощность множества — это соответствующий ему класс эквивалентности.
5.1.Мощность множества.
Эквивалентными (равномощными) называют два множества M и N, если между их элементами можно установить взаимно однозначное соответствие.
Можно дать и такое определение эквивалентности. Два непустых множества называются равномощными (эквивалентными), если существует биективное отображение одного из них на другое.
Определения мощности множества.
Класс эквивалентных множеств называется мощностью.
Или Мощностью множества М называют класс множеств, равномощных множеству М.
Если множества эквивалентны, то их мощности равны, то есть A B, или cardA = cardB,
где card A — мощность множества A. Для конечных множеств понятие мощности совпадает с понятием числа элементов множества. Мощность натуральных чисел (т.е. любого счетного множества) обозначается N0 (читается: "алеф нуль").
Ценность понятия мощности множества определяется существованием неравномощных бесконечных множеств. Например, множество всех подмножеств данного множества М имеет мощность большую, чем множество М.
Бесконечные множества
Основным свойством бесконечных множеств, отличающих их от конечныхявляетсято, что всякое бесконечное множество равномощно его собственному подмножеству, например |N| = |Z|. Из этого также вытекает, что множества точек двух, неравных по длине отрезков равномощны.
Чтобы в этом убедиться, возьмем два отрезка АВ и CD, затем с помощью вспомогательных биекций (перемещений) добьемся того, чтобы данные отрезки заняли положение отрезков ОМ и ON, показанных на рис. 9. Требуемая биекция между отрезками ОМ и ONможет быть взята в виде Р ↔ Q, где Р и Q- точки пересечения этих отрезков с прямыми, параллельными прямой NM.
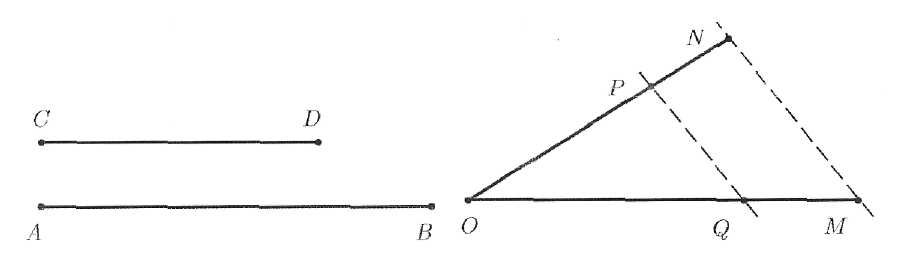
Рис.9 Биекция между отрезками прямых.
Напротив, т.к по определению Конечные множества 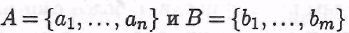 равномощны тогда и только тогда, когда множества А и В состоят из одного и того же числа элементов, т.е. п = т, то отсюда, в частности, следует, что конечное множество не является равномощным никакому своему собственному подмножеству. равномощны тогда и только тогда, когда множества А и В состоят из одного и того же числа элементов, т.е. п = т, то отсюда, в частности, следует, что конечное множество не является равномощным никакому своему собственному подмножеству.
Для мощностей бесконечных множеств, как и в случае конечных множеств, имеются понятия: равенства, больше, меньше. Т.е. для любых множеств A и B возможно только одно из трёх:
| A | = | B | или A и B равномощны;
| A | > | B | или A мощнее B, т. е. A содержит подмножество равномощное B, но A и B не равномощны;
| A | < | B | или B мощнее A, в этом случае B содержит подмножество равномощное A, но A и B не равномощны
Справедливо следующее утверждение:
-
Число подмножеств конечного множества, состоящего из n элементов равно 2n.
|
Доказательство проведем методом математической индукции.
База. Если n = 0, т. е. множество пусто, то у него только одно подмножество – оно само, и интересующее нас число равно 20 = 1.
Индукционный шаг. Пусть утверждение справедливо для некоторого n и пусть M – множество с кардинальным числом n + 1. Зафиксировав некоторый элемент , разделим подмножества множества M на два типа:
содержащие a0,
не содержащие a0, то есть являющиеся подмножествами множества .
Подмножеств типа (2) по предположению индукции 2n. Но подмножеств типа (1) ровно столько же, так как подмножество типа (1) получается из некоторого и притом единственного подмножества типа (2) добавлением элемента a0 и, следовательно, из каждого подмножества типа (2) получается этим способом одно и только одно подмножество типа (1).
Поэтому число всех подмножеств множества M равно 2n + 2n = 2n + 1.
Заметим, что 2A содержит подмножество, равномощное A (например, множество всех одноэлементных подмножеств A), а тогда из только что доказанного следует | 2A | > | A |
теорема Кантора гласит, что
-
Любое множество менее мощно, чем множество всех его подмножеств.
|
С помощью канторова квадрата можно также доказать следующее полезное утверждение:
-
Декартово произведение бесконечного множества A с самим собой равномощно A.
| |
|
|
 Скачать 2 Mb.
Скачать 2 Mb.




 r4
r4 
 10
10
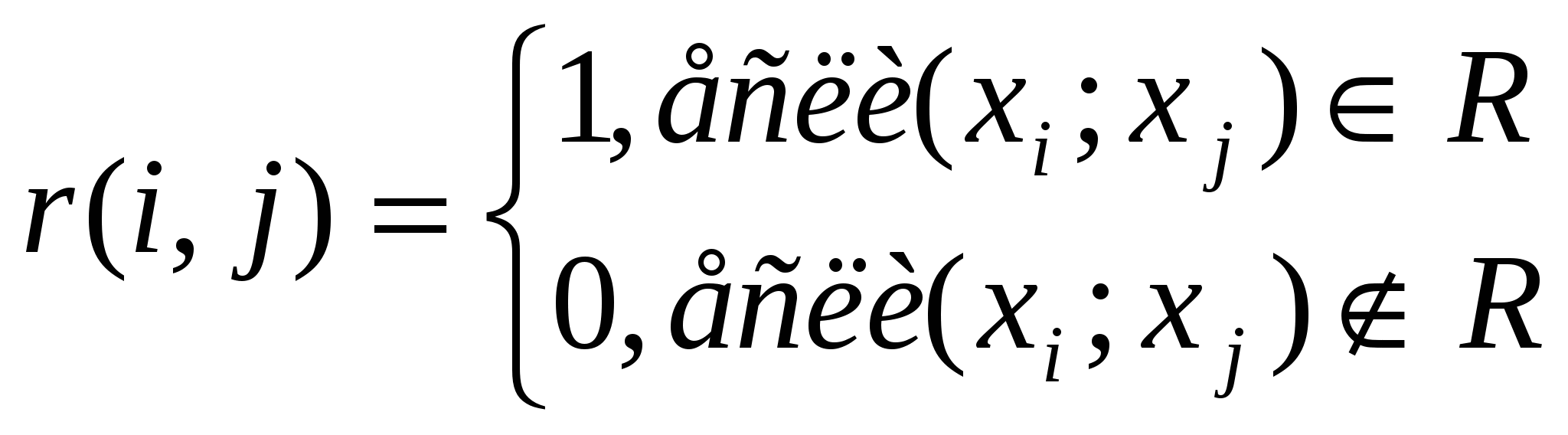
 ри графическом представлении отношения все элементы множества Х изображаются точками на плоскости листа и называются вершинами графа, а отношения между i-ым и j-ым элементами множества Х-линиями, которые называют ребрами ( или дугами) графа. В целом фигура, полученная на плоскости листа, называется графом. На рис.5 представлен граф для заданного множества целых чисел и отношения R4(xi;xj) ⊆Z.
ри графическом представлении отношения все элементы множества Х изображаются точками на плоскости листа и называются вершинами графа, а отношения между i-ым и j-ым элементами множества Х-линиями, которые называют ребрами ( или дугами) графа. В целом фигура, полученная на плоскости листа, называется графом. На рис.5 представлен граф для заданного множества целых чисел и отношения R4(xi;xj) ⊆Z.

