Алгебраические числа (A) - это корни алгебраических уравнений
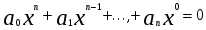
с рациональными (целыми) коэффициентами.
Пусть R - множество действительных чисел,
Q - множество рациональных чисел,
J - множество иррациональных чисел,
А - множество алгебраических чисел,
T - множество неалгебраических (трансцендентных) чисел.
Тогда:
R=Q J и из того, что множество R является континуальным, то тем самым доказывается существование иррациональных чисел, более того, множество иррациональные числа представляют собой континуальное множество, в то время как множество рациональных чисел (как это было показано ранее) счетно; J и из того, что множество R является континуальным, то тем самым доказывается существование иррациональных чисел, более того, множество иррациональные числа представляют собой континуальное множество, в то время как множество рациональных чисел (как это было показано ранее) счетно;
R=A T и из того, что множество R является континуальным, то тем самым доказывается существование неалгебраических (трансцендентных) чисел, более того, множество трансцендентных числа представляют собой континуальное множество, в то время как множество алгебраических чисел (как это было показано ранее) счетно. T и из того, что множество R является континуальным, то тем самым доказывается существование неалгебраических (трансцендентных) чисел, более того, множество трансцендентных числа представляют собой континуальное множество, в то время как множество алгебраических чисел (как это было показано ранее) счетно.
Примерами трансцендентных чисел являются числа: e, 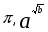 (число Эйлера) , где а -иррациональное число, а в - целое, с=0,1234567891011...(число Малера) и др. (число Эйлера) , где а -иррациональное число, а в - целое, с=0,1234567891011...(число Малера) и др.
И снова житейский парадокс. Мощность континуума имеет,
например, множество точек прямой или множество действительных
чисел, что то же самое. Более того, любой отрезок числовой оси,
даже такой малюсенький отрезок, как отрезок от 0 до 1, имеет
мощность континуума, то есть на нем больше чисел, чем найдется
чисел в счетном множестве. А раз этот отрезок имеет мощность
континуума, как и вся (бесконечная) прямая и, естественно, любой
ее отрезок, то можно сказать, что на отрезке от 0 до 1 ровно
столько же точек, сколько на отрезке прямой от Земли до Юпитера.
. Дополнить задачами из папки практ_зан_по теор_множеств/z2.pdf
5.4. Дополнение.
Разбиения. Классы эквивалентности. Фактормножества.
Разбиения. Классы эквивалентности.
О п р е д е л е н и е 1. Разбиением множества А называют любое семейство 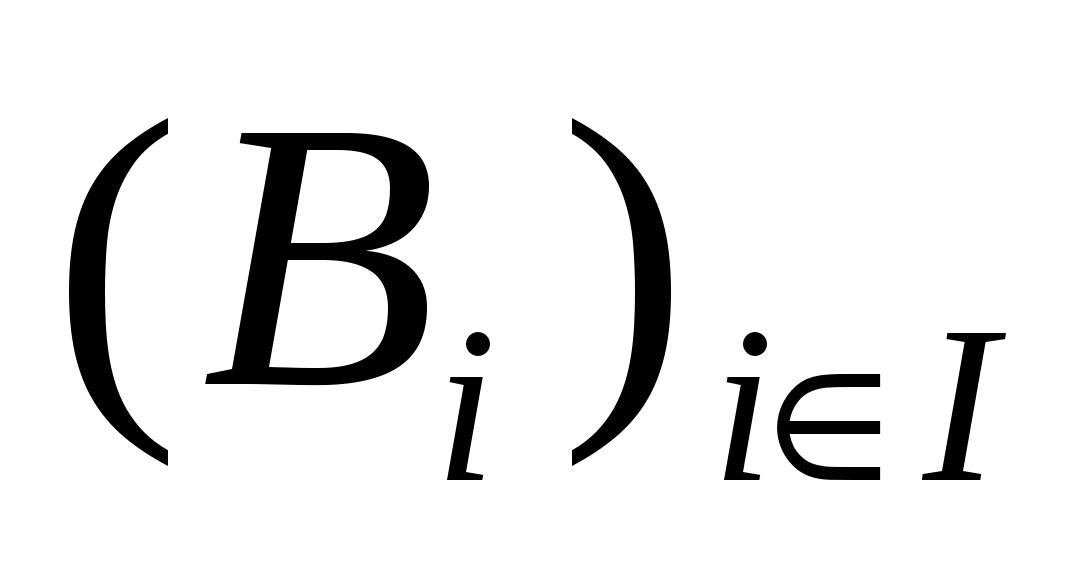 непустых и попарно непересекающихся множеств, если объединение множеств семейства непустых и попарно непересекающихся множеств, если объединение множеств семейства 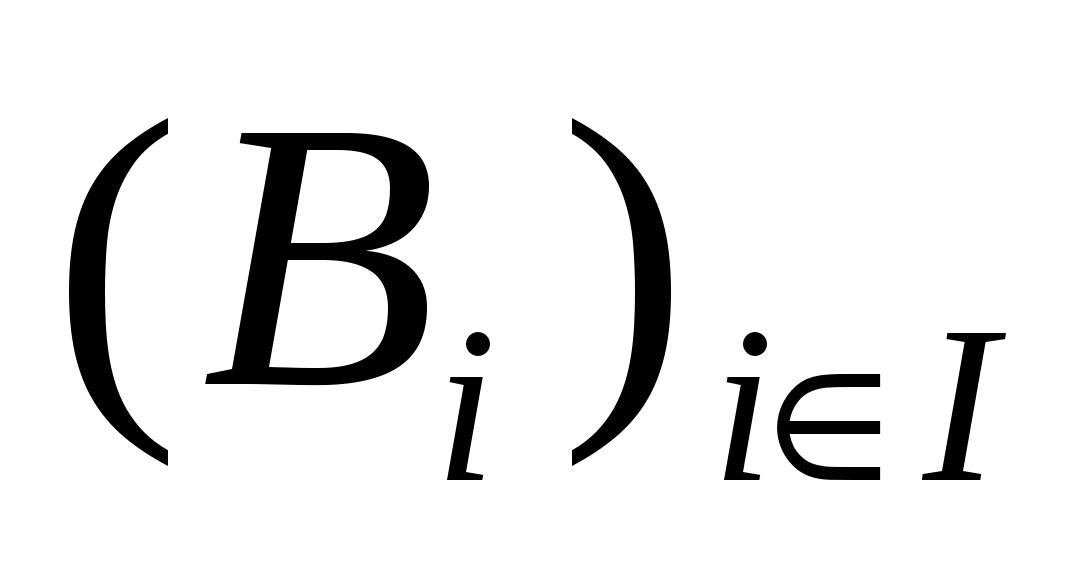 равно А, т.е. равно А, т.е. 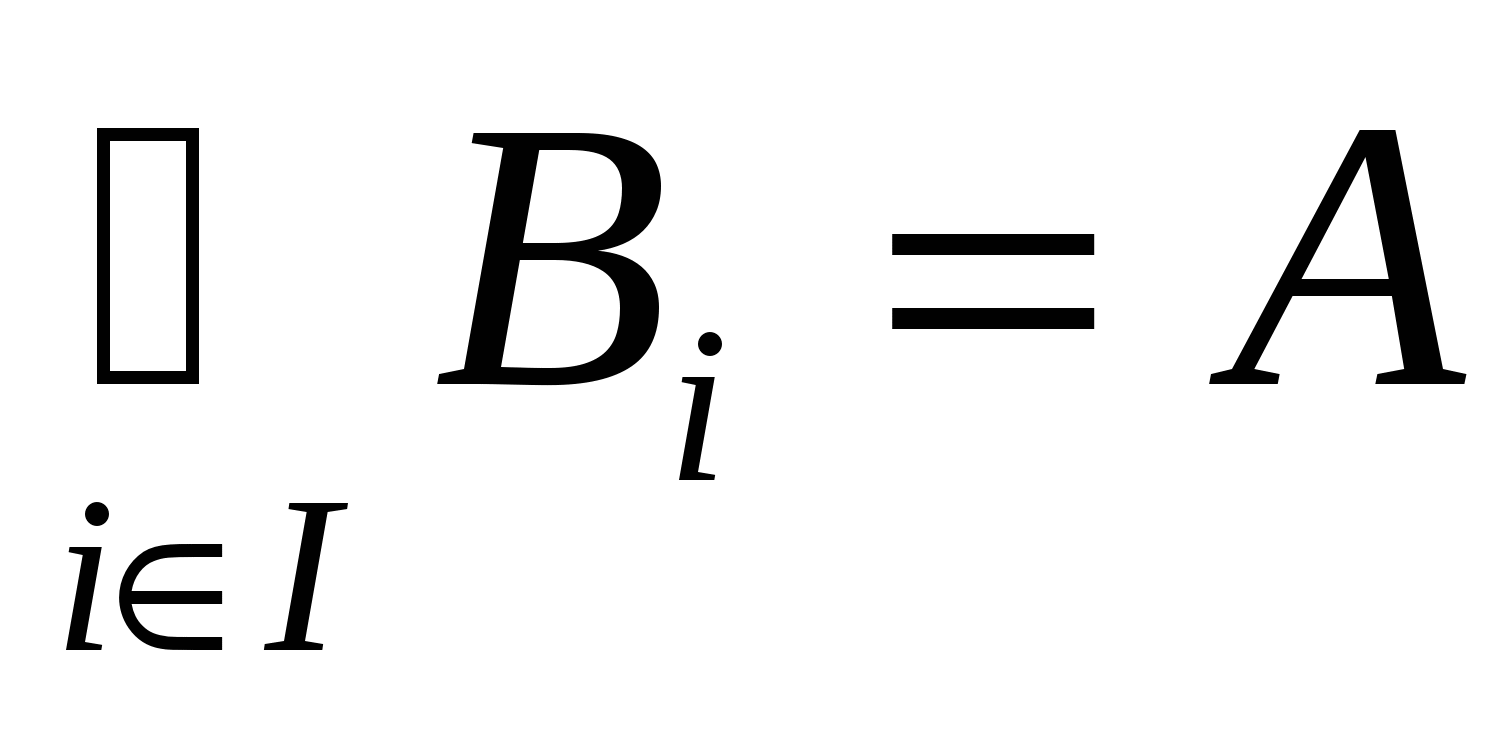 . .
Сами множества Bi называют элементами разбиения 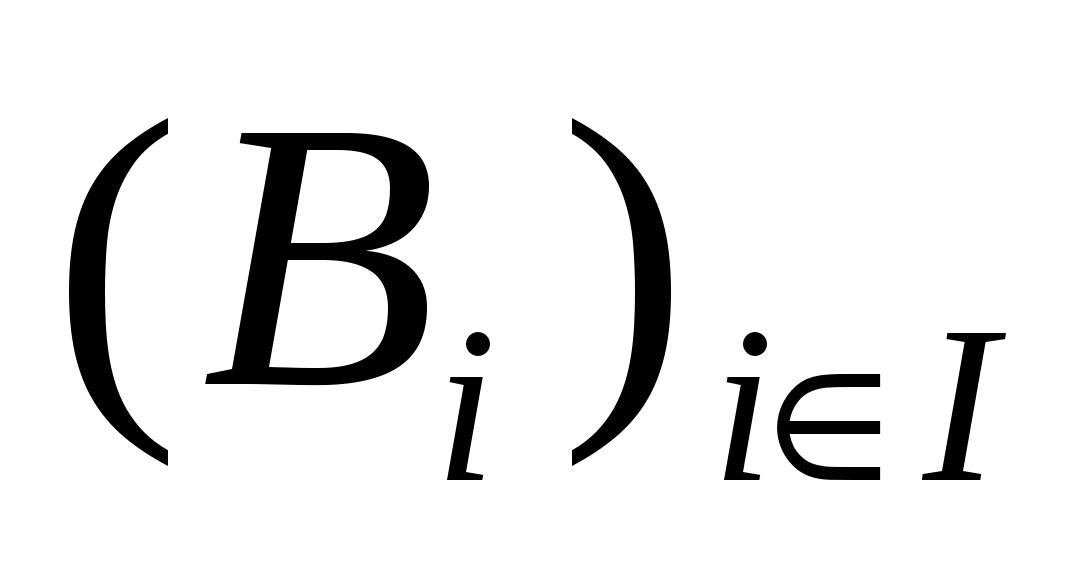 . .
Например, множества 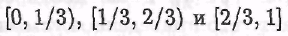 образуют разбиение отрезка [0,1]. образуют разбиение отрезка [0,1].
Пусть на множестве А задано отношение эквивалентности R. Тогда можно разбить множество А на классы эквивалентных элементов. Действительно, возьмем произвольный элемент 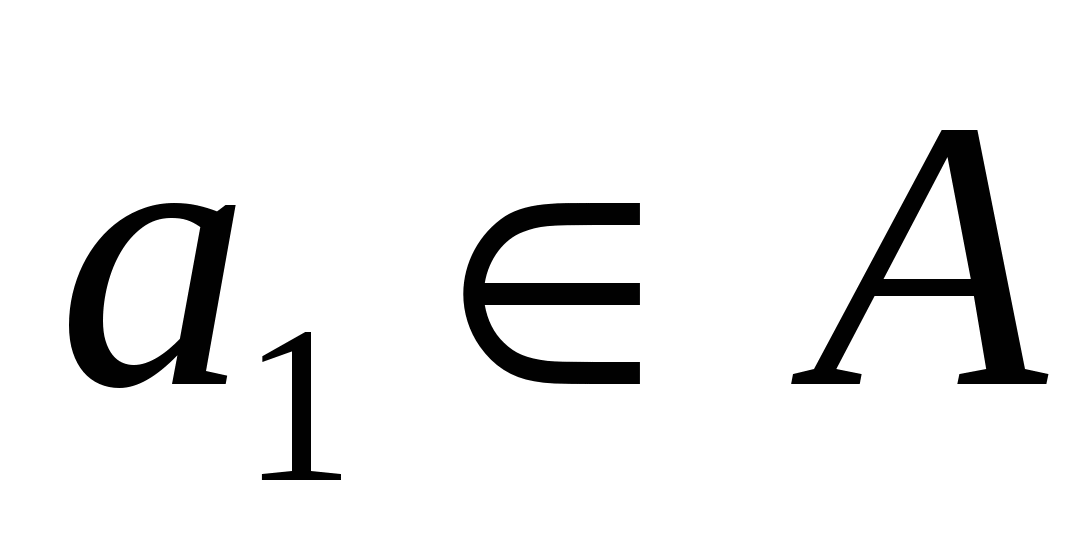 и образуем класс В1, состоящий из а1и всех элементов, эквивалентных а1. Затем выберем и образуем класс В1, состоящий из а1и всех элементов, эквивалентных а1. Затем выберем 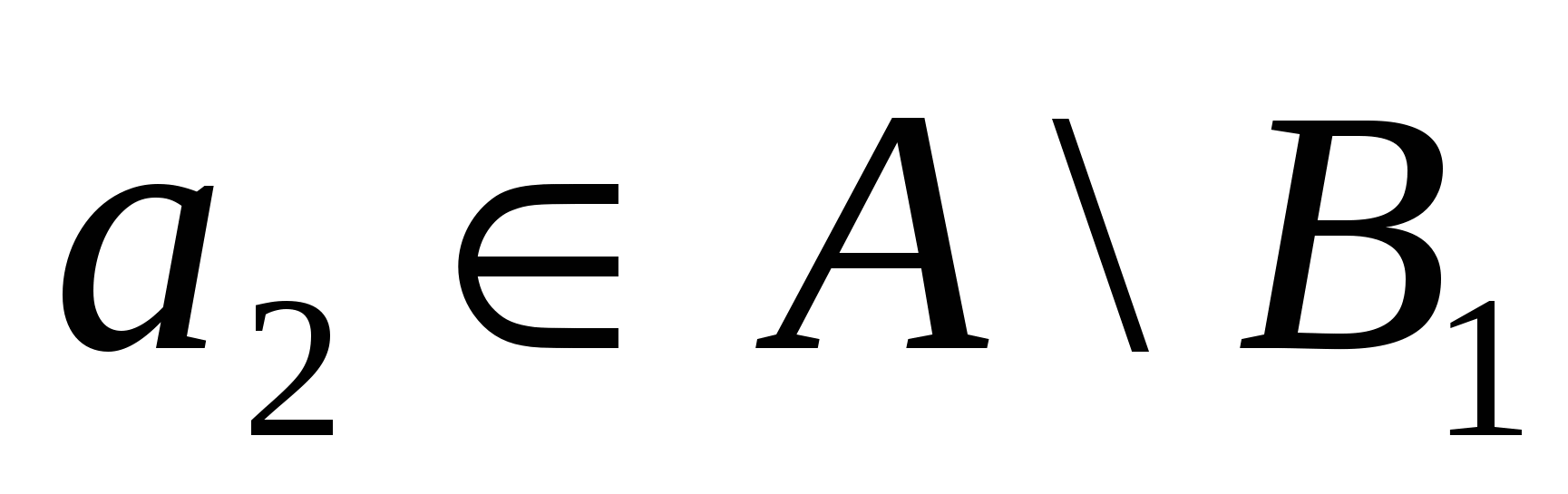 (если такой найдется) и образуем класс В2 , состоящий из а2 и всех элементов, эквивалентных а2 и т.д. Получается система классов В1, В2,…. (возможно бесконечная) такая, что любой элемент из А входит хотя бы в один класс, т.е. (если такой найдется) и образуем класс В2 , состоящий из а2 и всех элементов, эквивалентных а2 и т.д. Получается система классов В1, В2,…. (возможно бесконечная) такая, что любой элемент из А входит хотя бы в один класс, т.е.
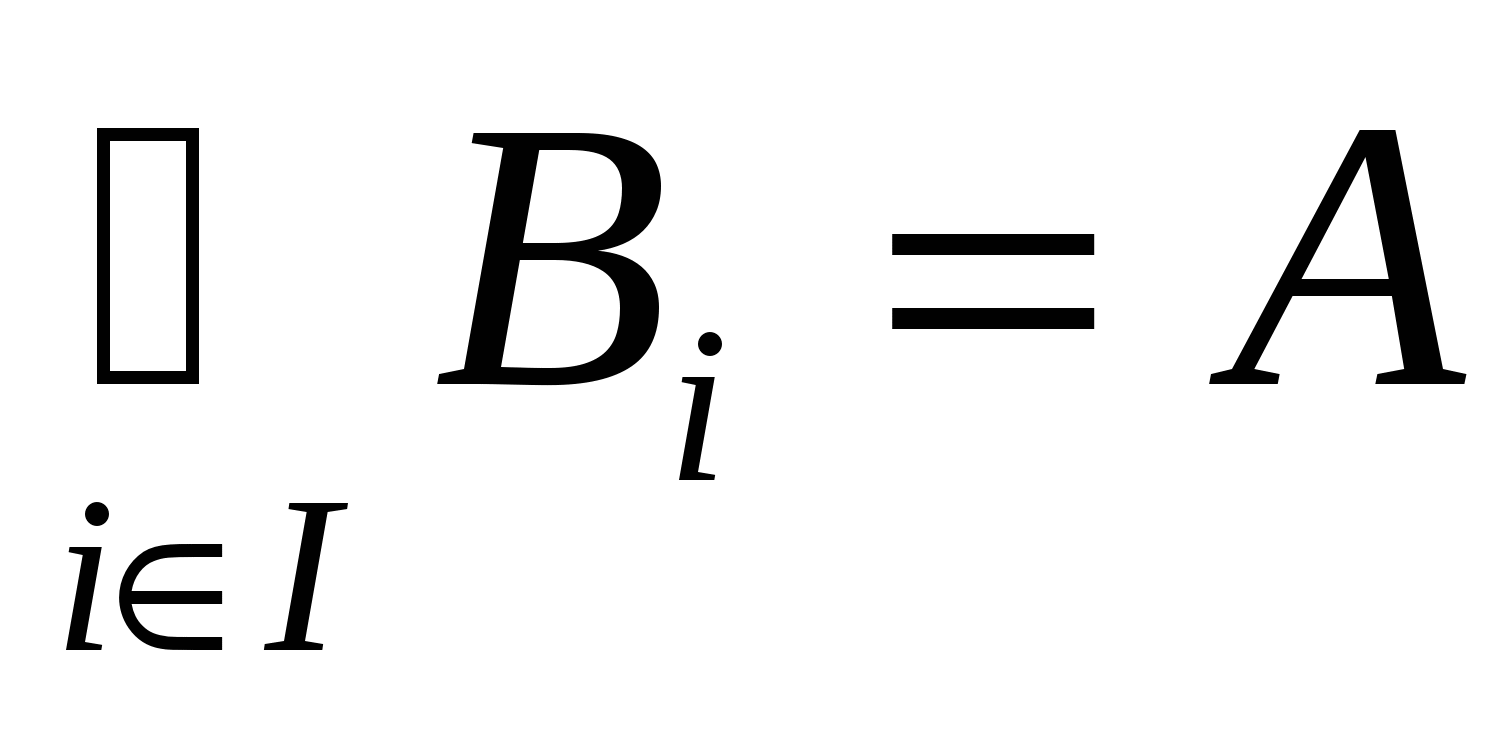
Эта система классов обладает следующими легко проверяемыми свойствами:
система образует разбиение А, такое, что классы попарно не пересекаются;
любые два элемента из одного класса эквивалентны;
любые два элемента из разных классов неэквивалентны.
Построенное разбиение, т.е. система классов называется системой классов эквивалентности по отношению к R .
С другой стороны, любое разбиение А на классы определяет некоторое отношение эквивалентности, а именно, отношение "входить в один и тот же класс данного разбиения".
П р и м е р.
Все классы эквивалентности D по отношению равенства состоят из одного элемента.
Разбиение множества треугольников на классы эквивалентности по отношению подобия.
Разбиение N по отношению "иметь общий остаток от деления на 3":
В0 = {3,6,9,...}, В1 ={1,4,7,...}, В2 ={2,5,8,...}.
Дадим более строгое математическое определение классов эквивалентности.
О п р е д е л е н и е 2. Пусть А некоторое множество, а R отношение эквивалентности на множестве А. Для каждого элемента  определим подмножество Ка множества А следующим образом определим подмножество Ка множества А следующим образом
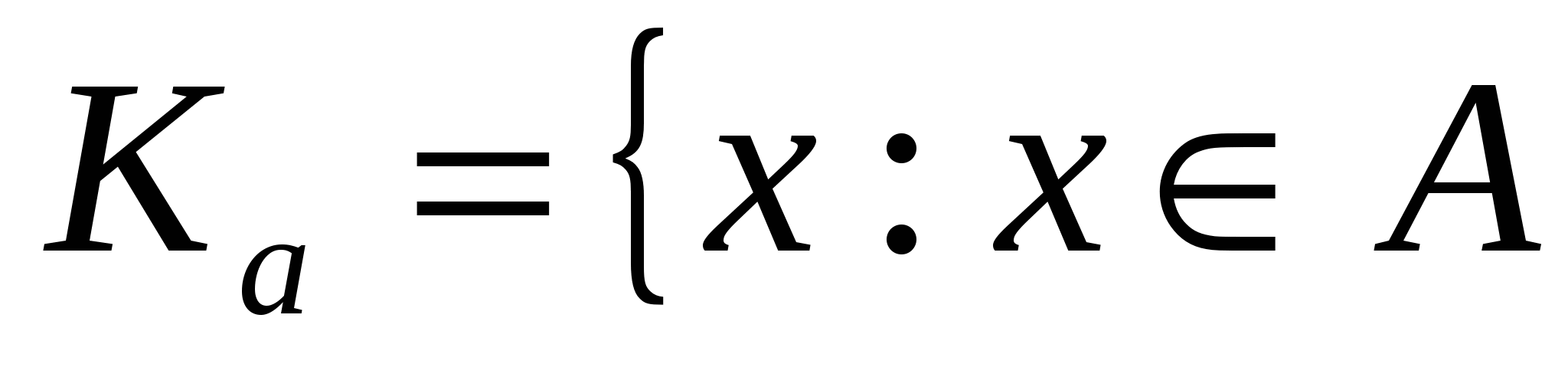 и и 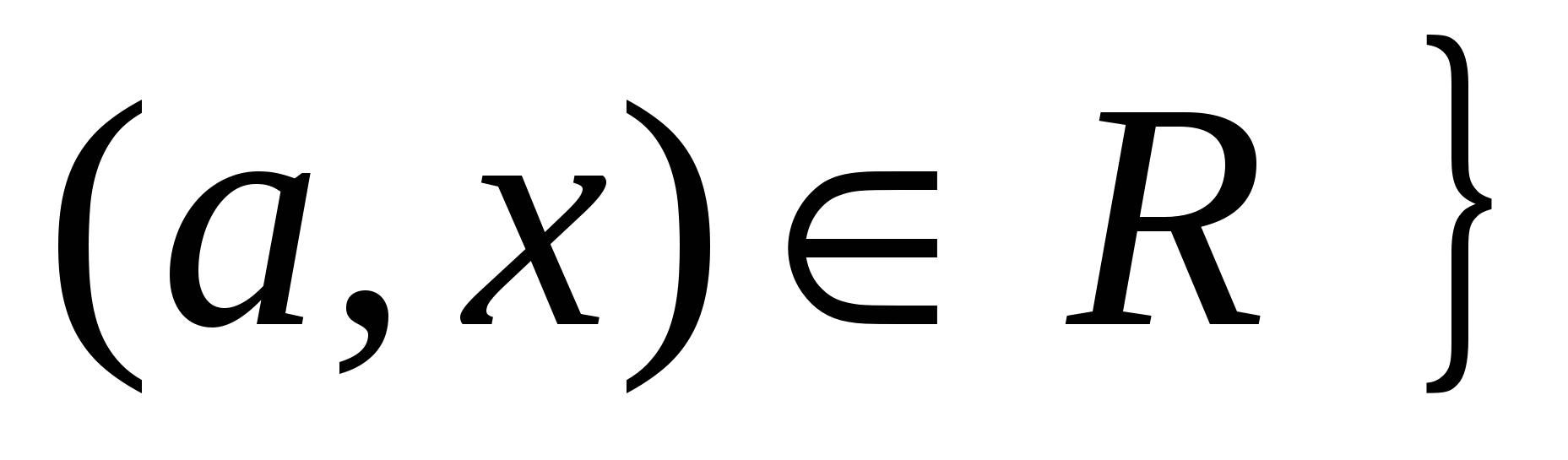
Подмножество Каназовем классом эквивалентности множества А по R, относительно элемента а. Элемент а назовем представителем этого класса.
Коротко это понятие можно сформулировать так:
Классом эквивалентности элемента a называется подмножество элементов, эквивалентных a.
Замечание. Далее отношение эквивалентности часто будем обозначать знаком
.
П р и м е р. Пусть А ={1,2,3} и R = {(1,1),(2,2,),(3,3),(1,3),(3,1)}, тогда К1 =К3={1,3}, К2={2}.
Т е о р е м а 1. Любые два класса эквивалентности либо не пересекаются, либо совпадают.
Доказательство.
Пусть два класса эквивалентности Ka и Kb имеют общий элемент с т.е. 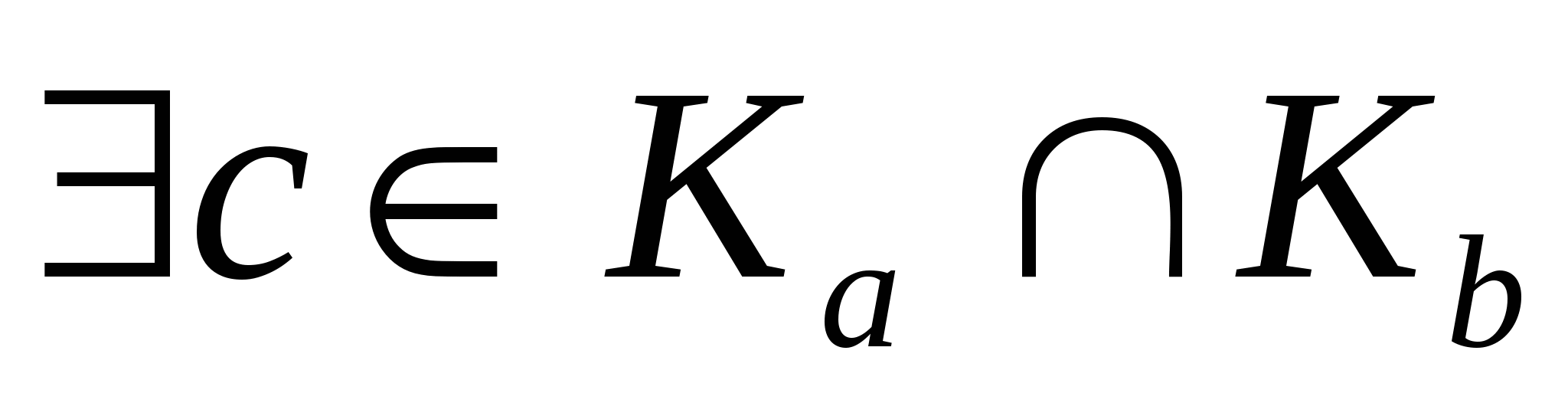 . Тогда с . Тогда с
а и с
b. В силу симметричности отношения
имеем а
с и с
b. В силу транзитивности отношения
получим а
b.
Пусть 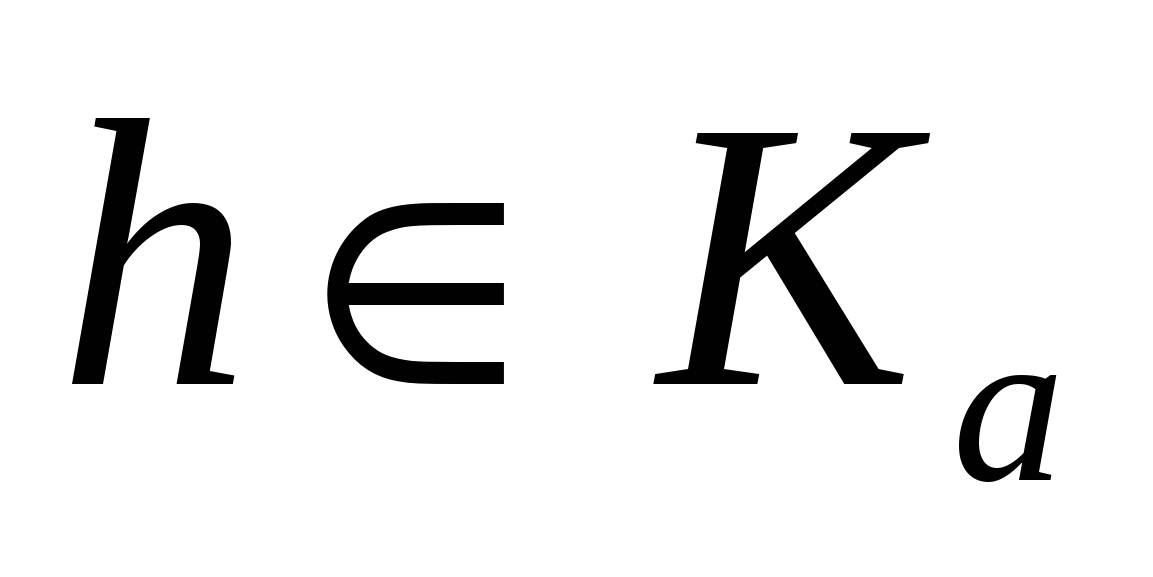 , тогда h , тогда h
a. Так как а
b, то h
b и, следовательно 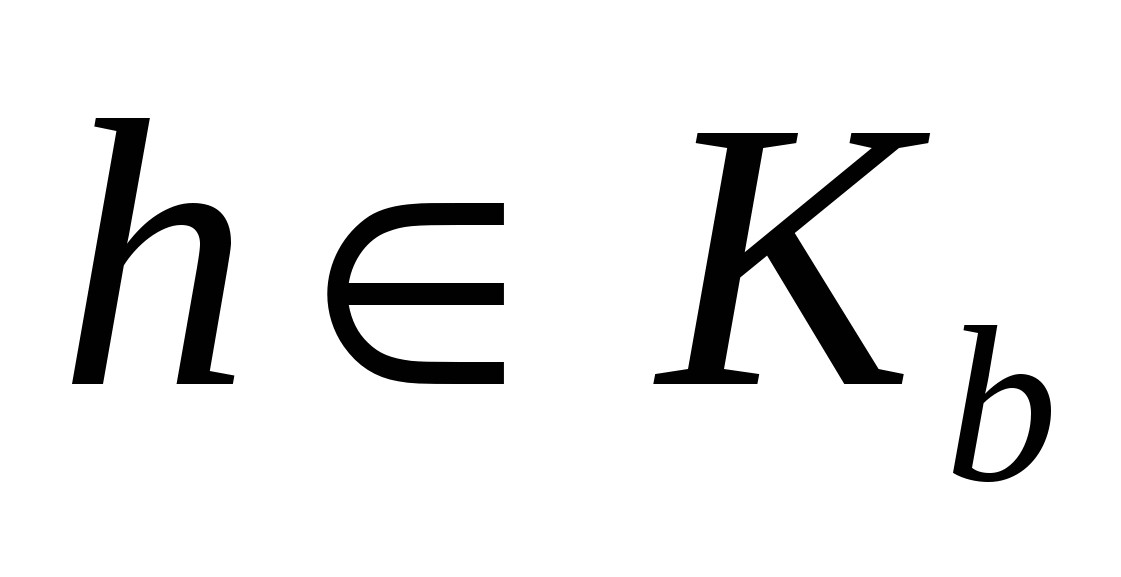 . .
Если же 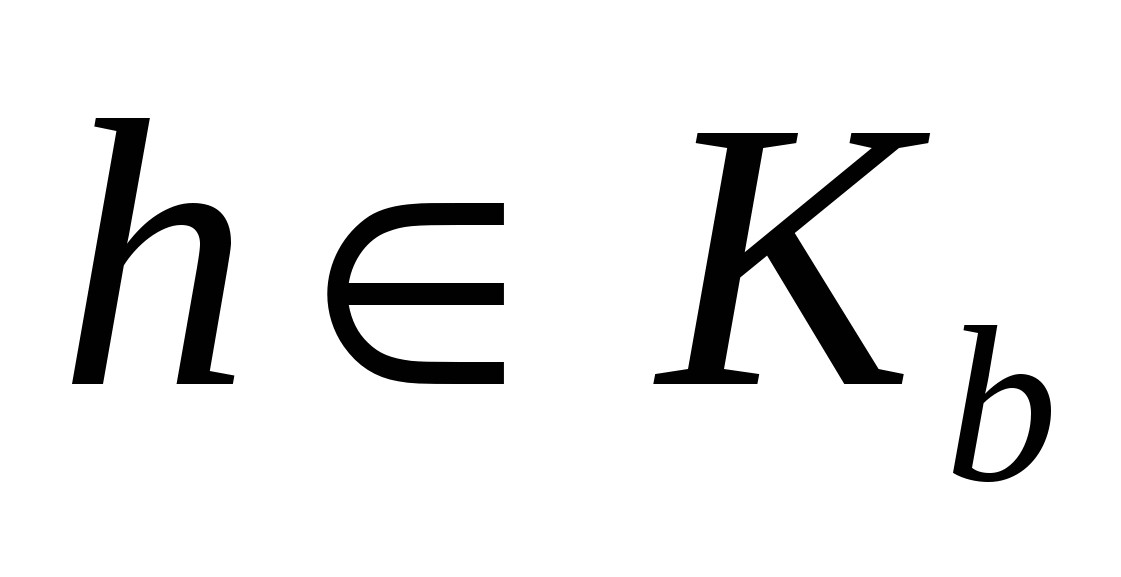 , то в силу симметричности , то в силу симметричности
получим h
b, b
a и в силу транзитивности - h
a, т.е. 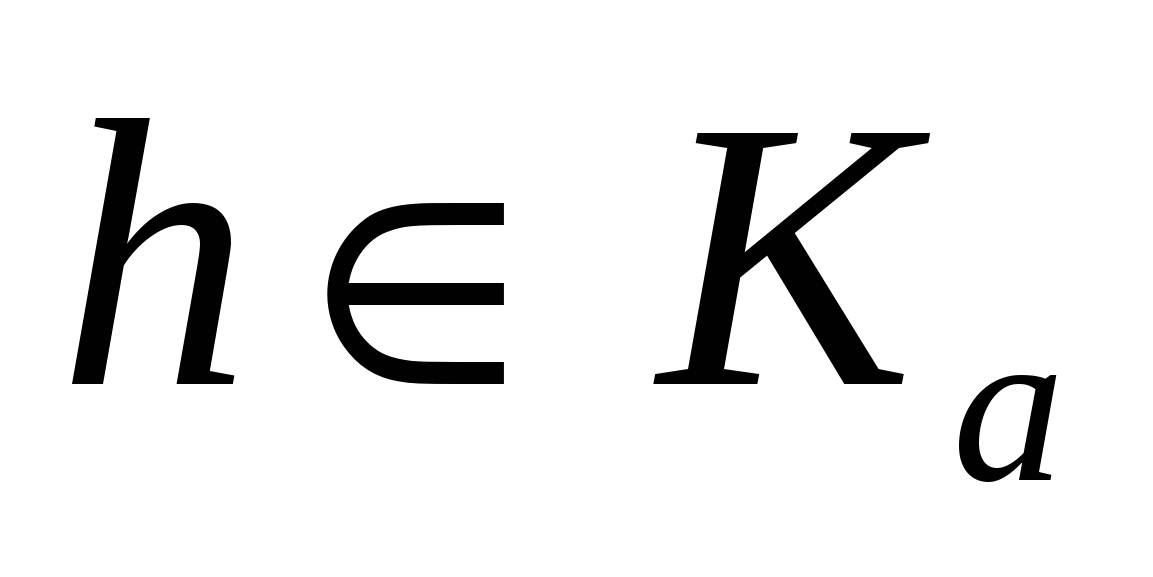 . .
Таким образом, Ka =Kb.
Фактормножества.
О п р е д е л е н и е 3. Пусть А – некоторое множество, а R – эквивалентность на А. Множество всевозможных классов эквивалентности множества А по отношению R называется фактормножеством множества А по отношению Rи обозначается А/R(не путать с A\R).
Т е о р е м а 2. Пусть А — множество, a R , R1 , R2 — эквивалентности на А. Тогда:
A/R является разбиением множества А;
Если эквивалентности R1 и R2 на множестве А различны, то различны и фактормно-
жества A/R1 и А/R2.
Доказательство. (не приводить)
Так как R— эквивалентность на А, то из теоремы 1 следует, что два различных класса по Rне пересекаются. Далее, так как объединение всех классов по Rсовпадает со всем множеством А, то, согласно определению 1, фактормножество A/Rявляется разбиением А.
Пусть R1 ≠R2. Значит R1и R2 состоят из различных пар. Пусть, для определенности, 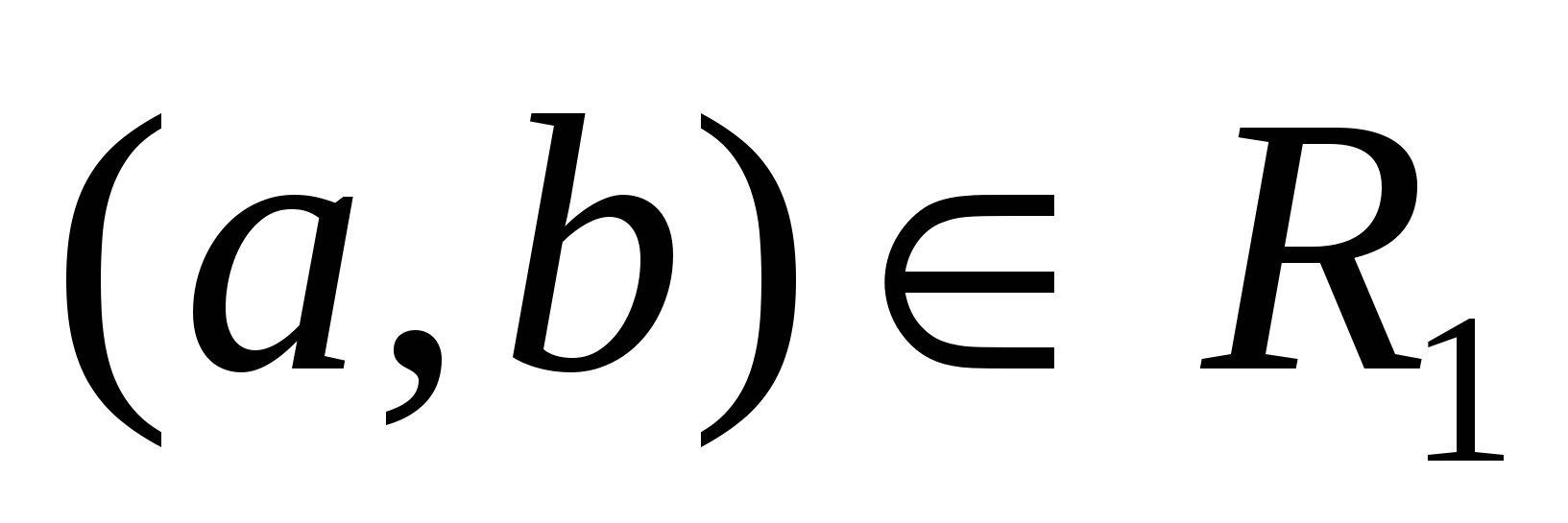 и и 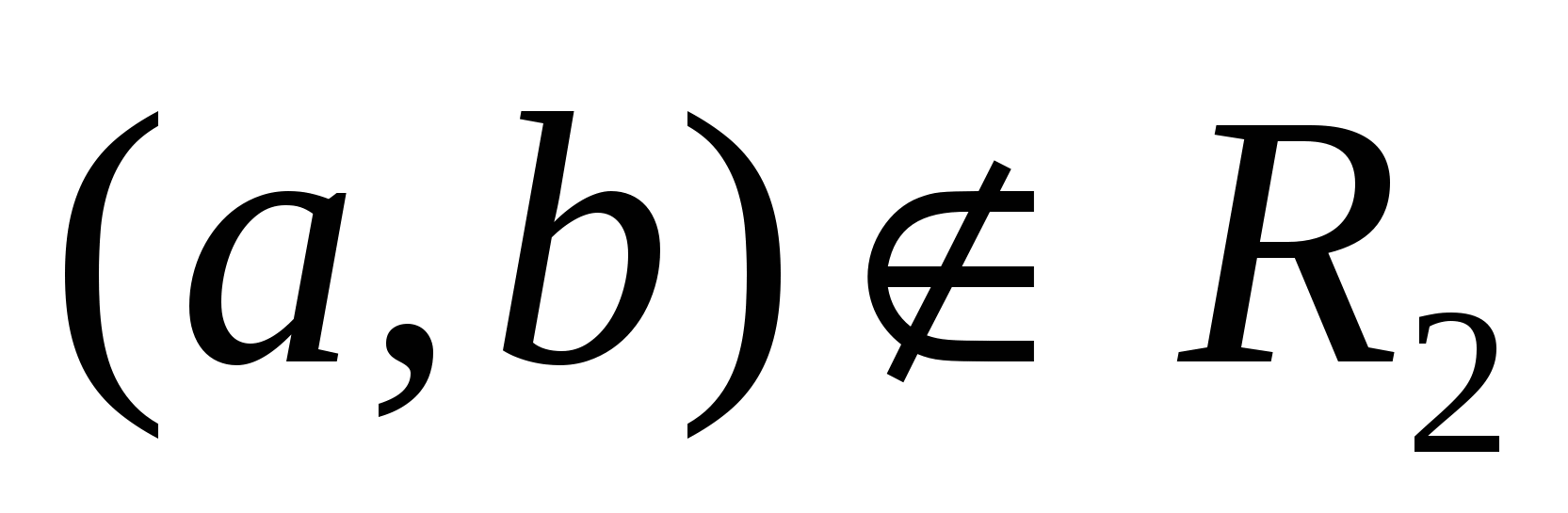 , где , где 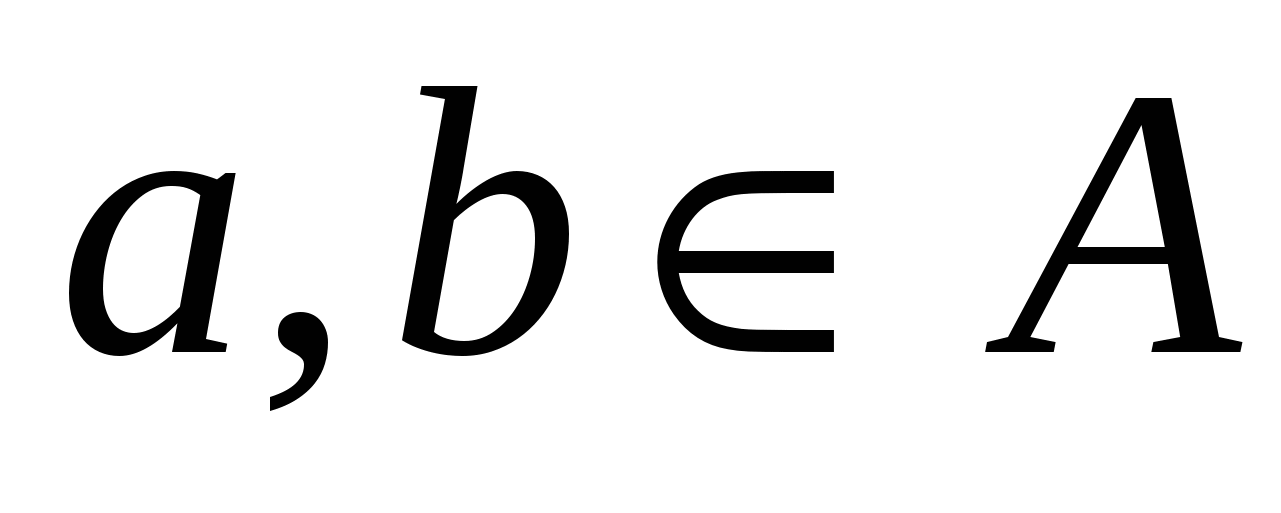 . Предположим, что . Предположим, что 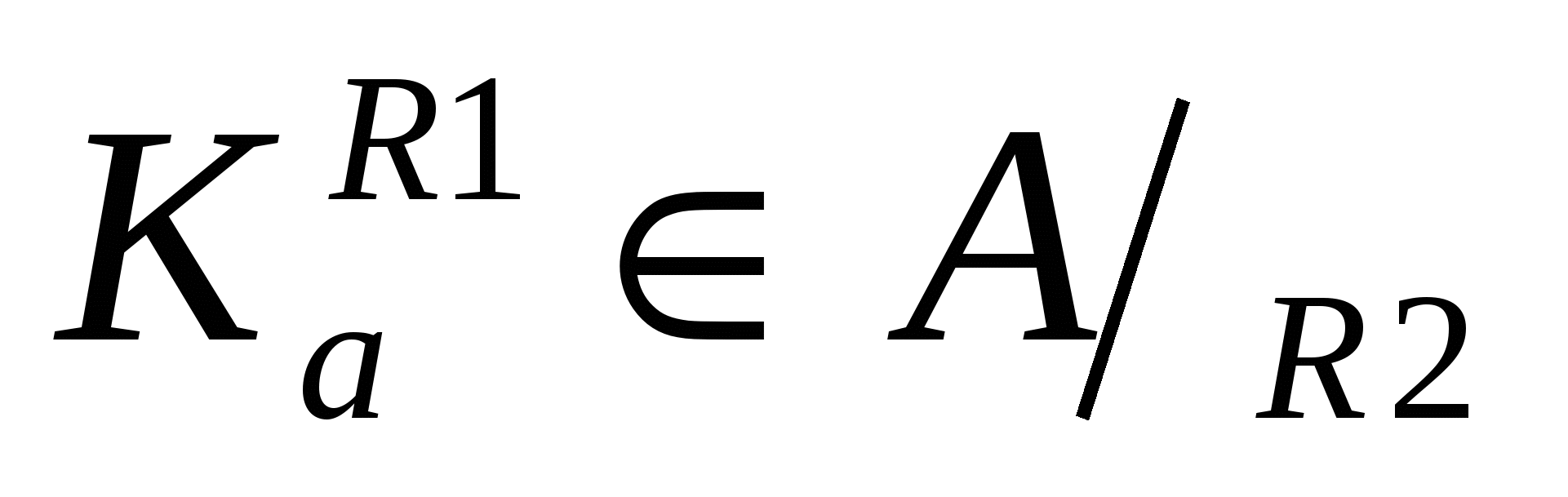 . Значит найдется . Значит найдется 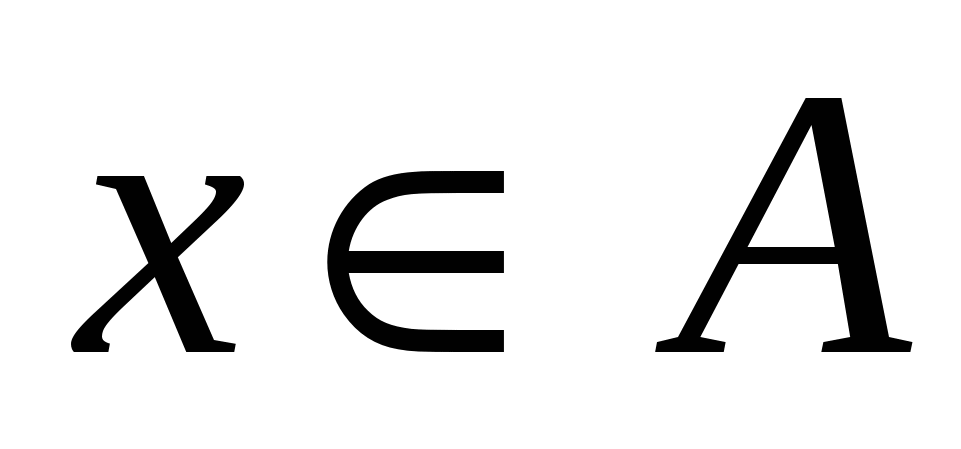 такой, что такой, что 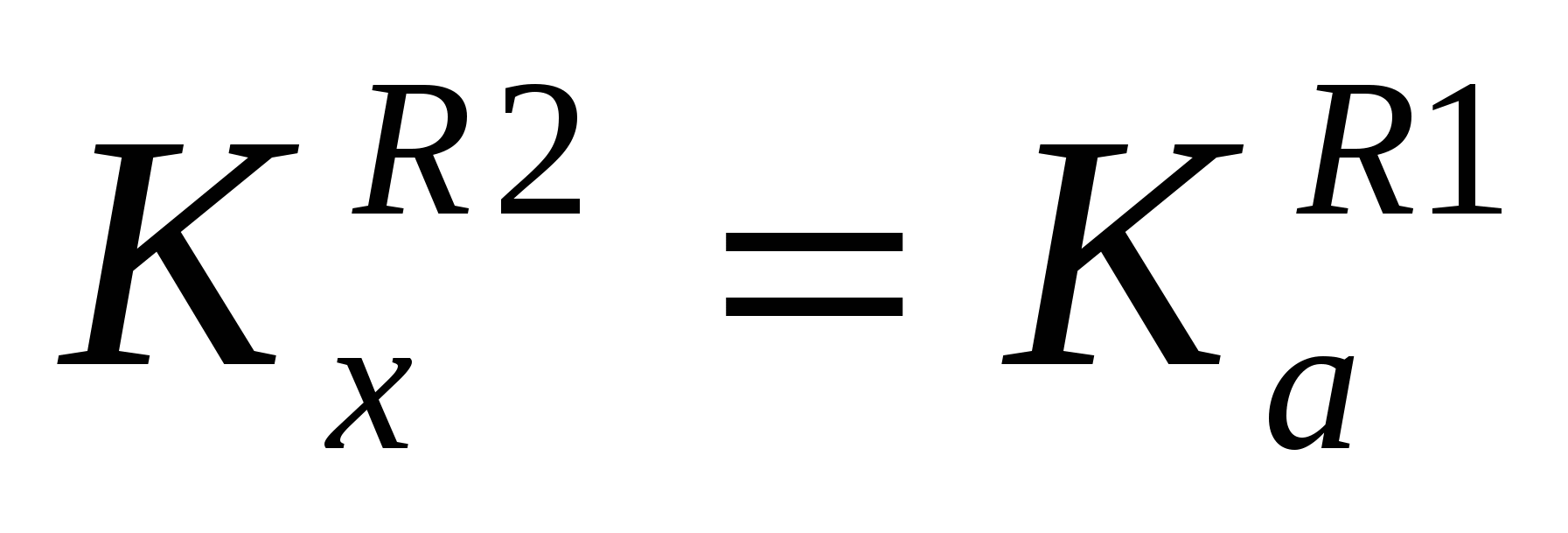 . Так как . Так как 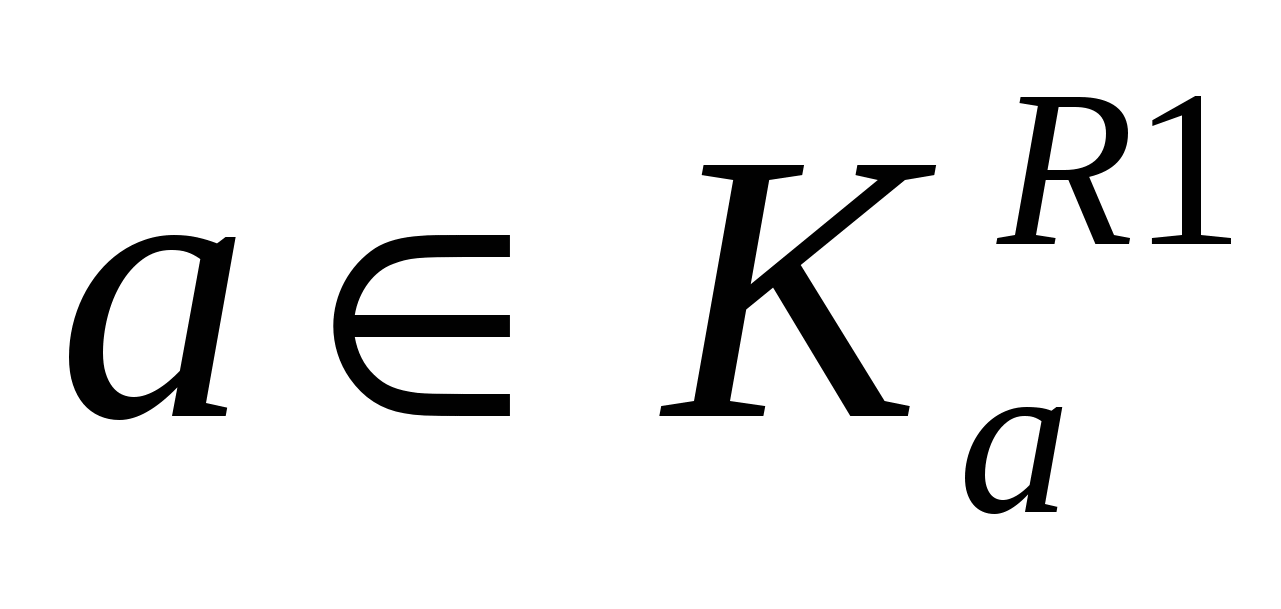 , то , то 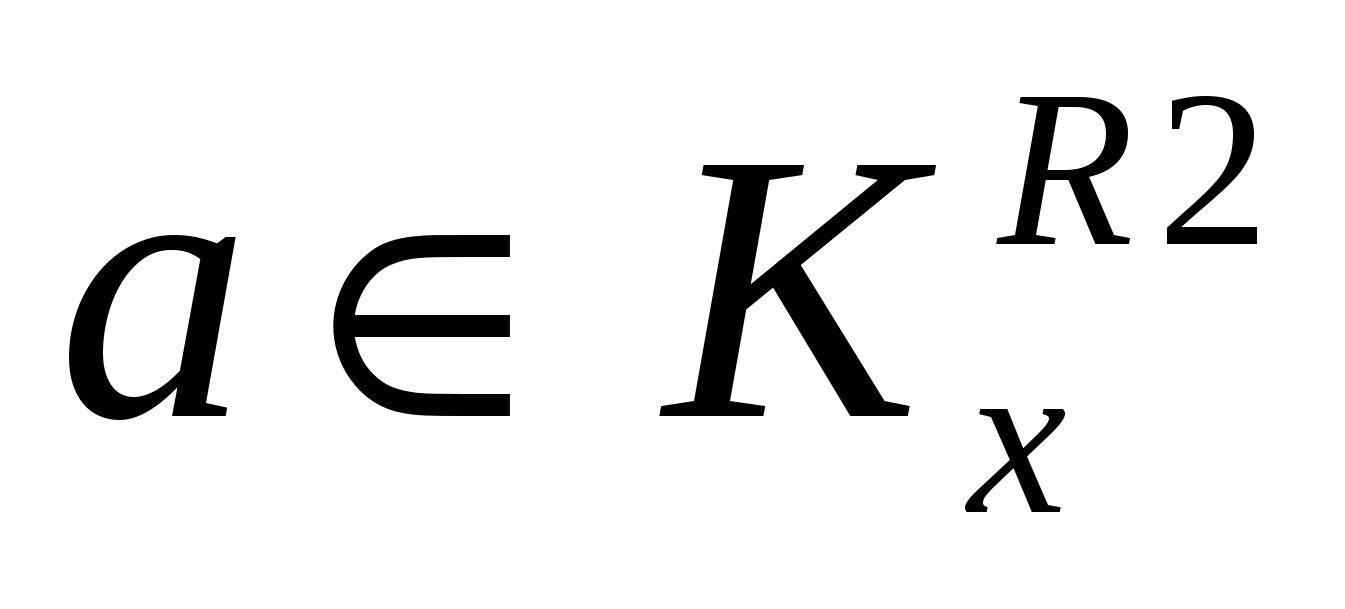 . Это означает, что для любого . Это означает, что для любого 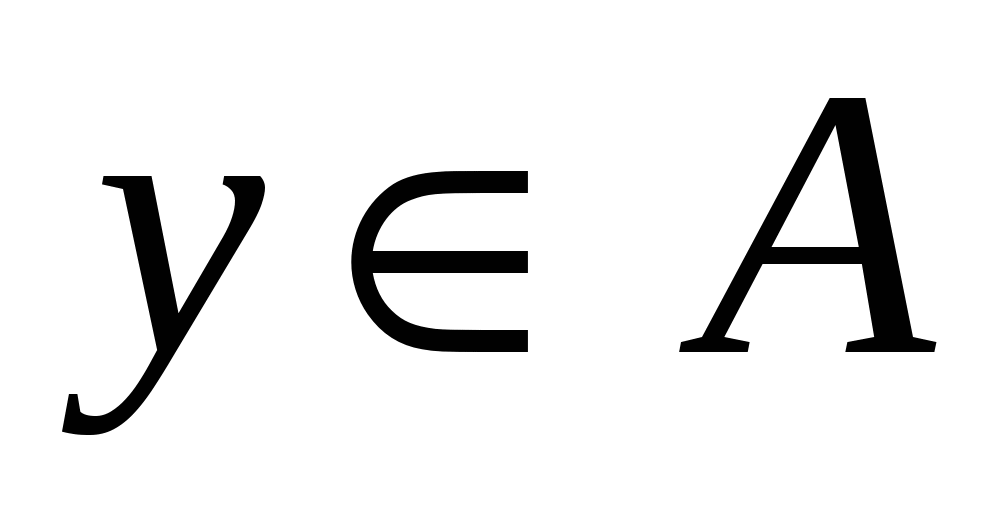 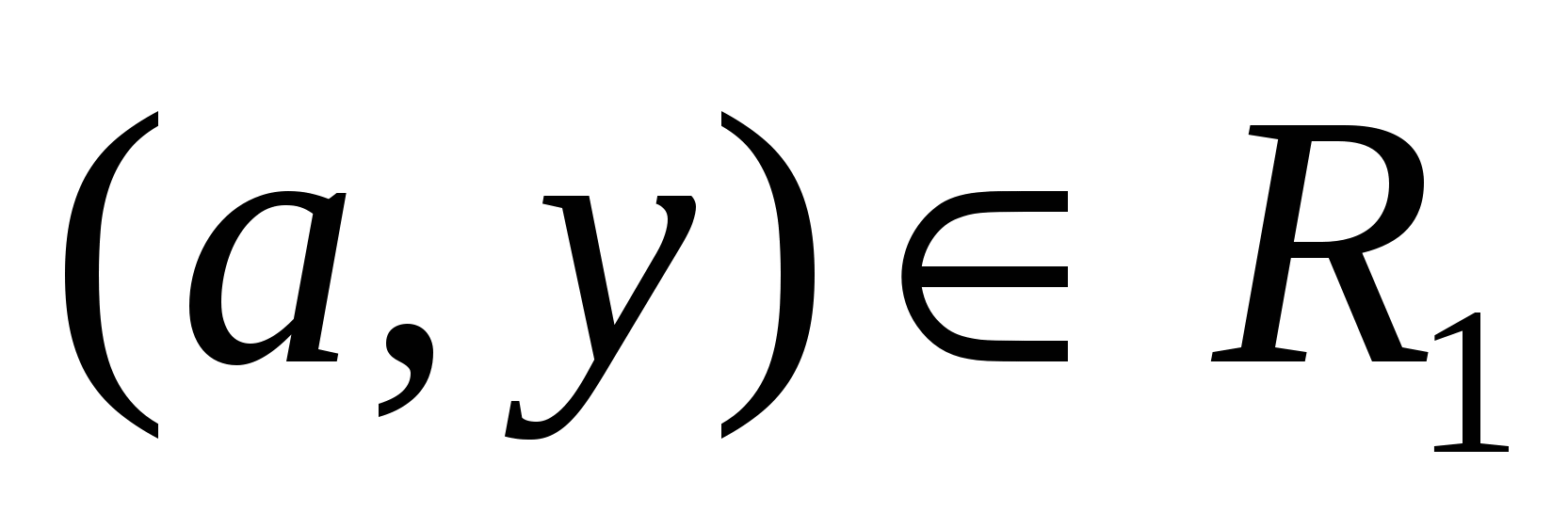 тогда и только тогда, когда тогда и только тогда, когда 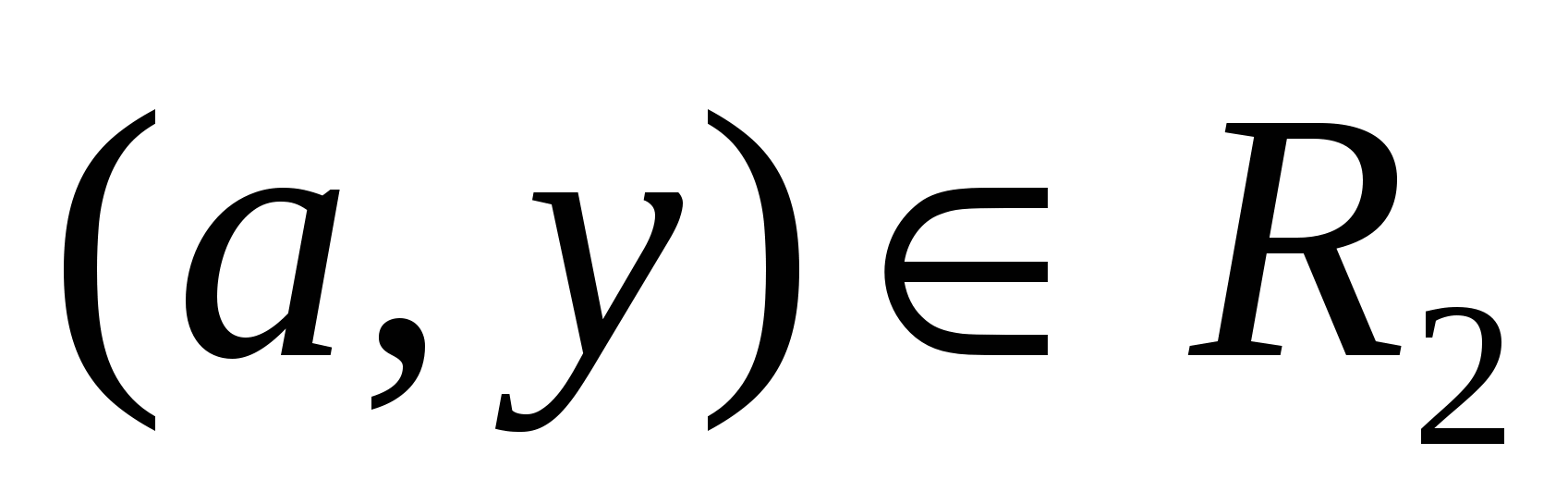 . Однако, для у = bэто не так. Значит наше предположение неверно, то есть . Однако, для у = bэто не так. Значит наше предположение неверно, то есть 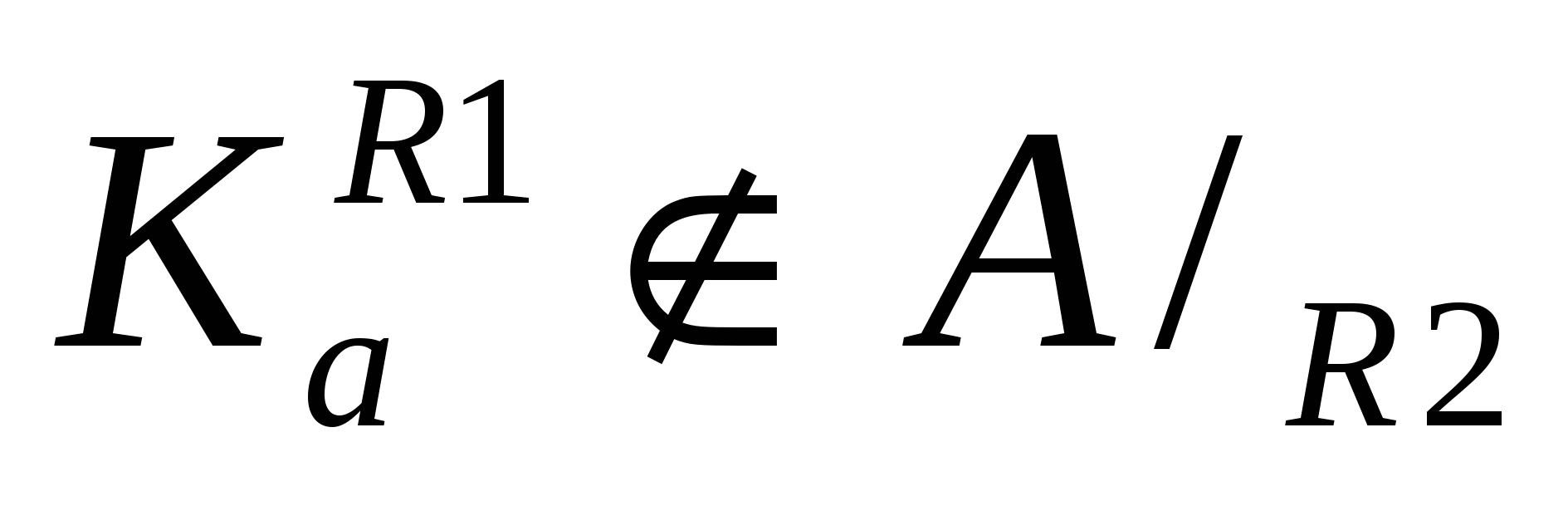 .Но, так как .Но, так как  , то , то 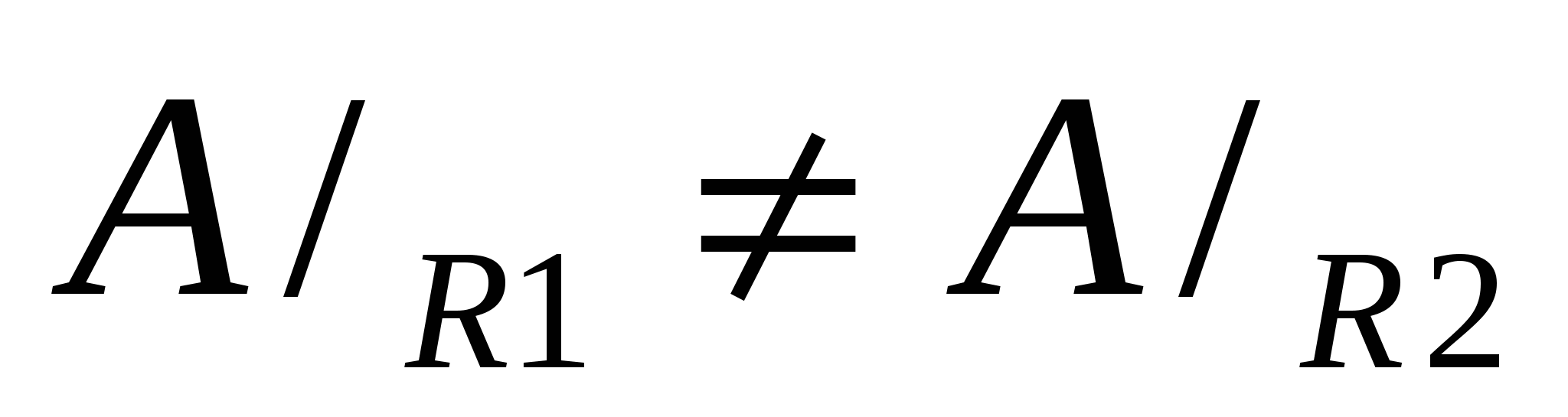 . .
Т е о р е м а 3. Для всякого разбиения 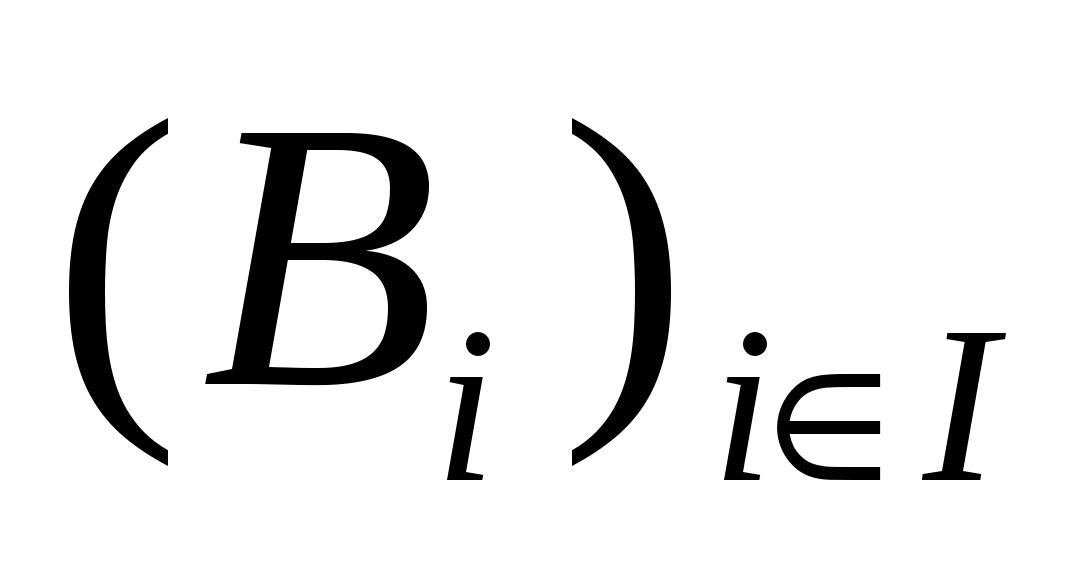 множества А существует единственная эквивалентность R на А такая, что множества А существует единственная эквивалентность R на А такая, что 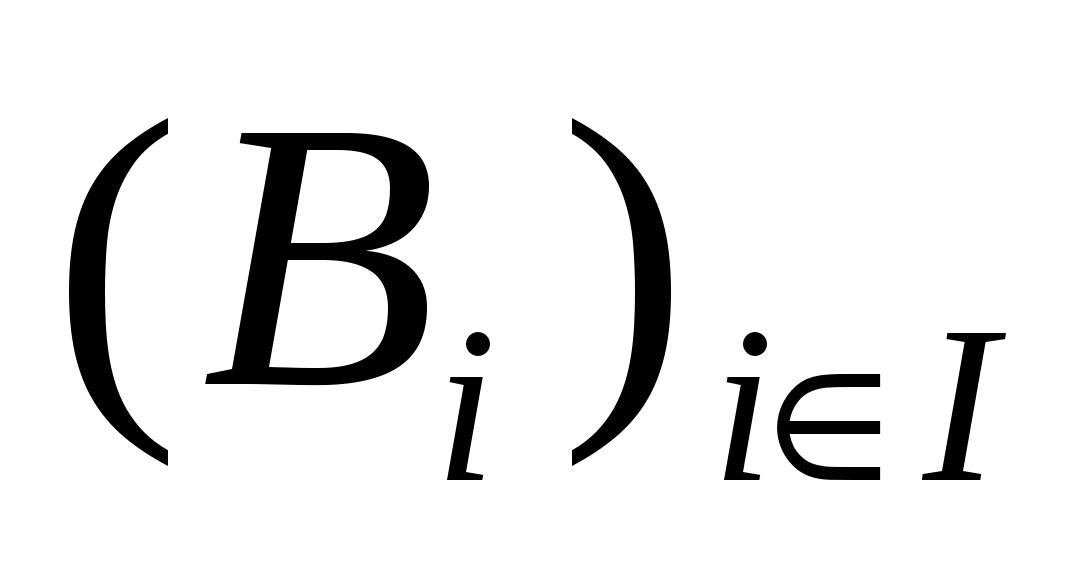 = A/R. И наоборот. = A/R. И наоборот.
Таким образом, эта теорема отождествляет понятия эквивалентности и разбиения: любая эквивалентность определяет единственное разбиение и наоборот.
Доказательство. Построим бинарное отношение R следующим образом: для любых элементов 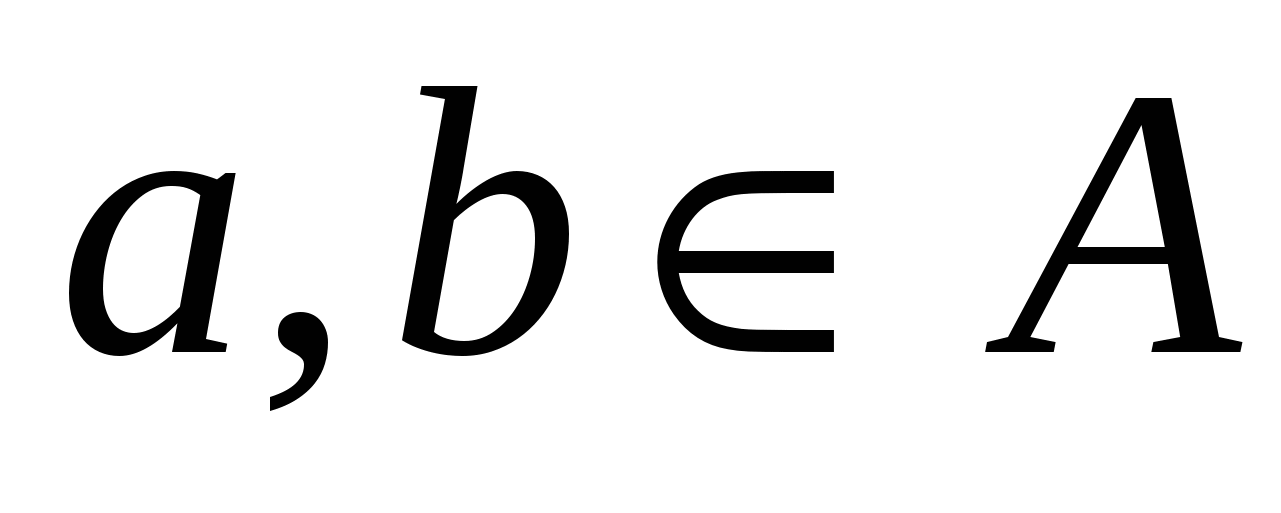 , пара , пара 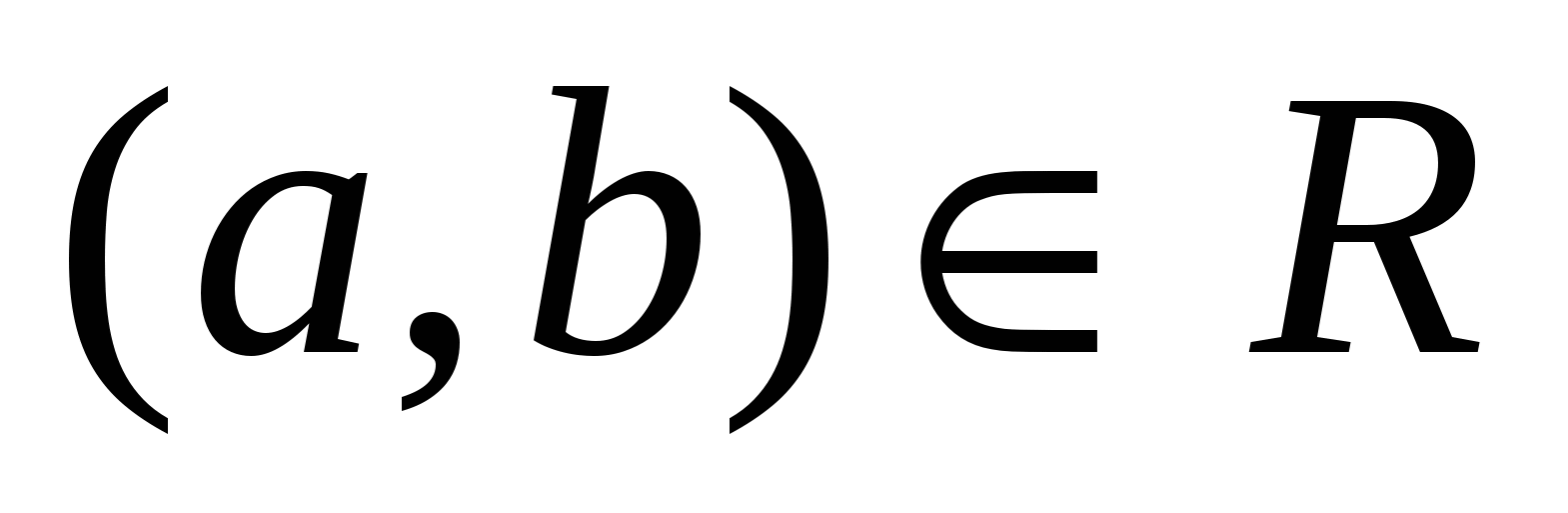 тогда и только тогда, когда a и b принадлежат одному и тому же подмножеству из тогда и только тогда, когда a и b принадлежат одному и тому же подмножеству из 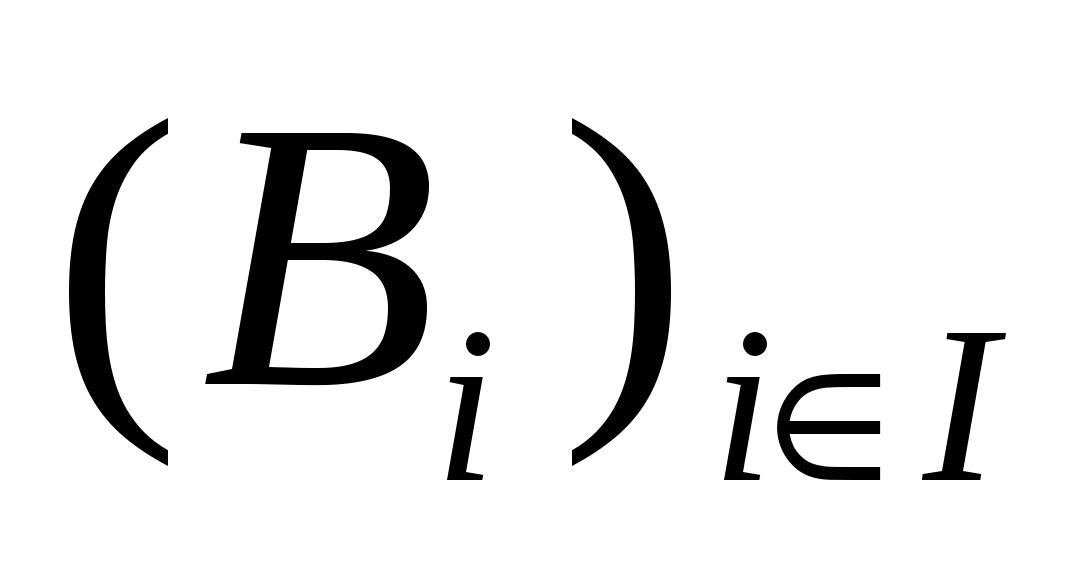 . Легко понять, что R является отношением эквивалентности и . Легко понять, что R является отношением эквивалентности и 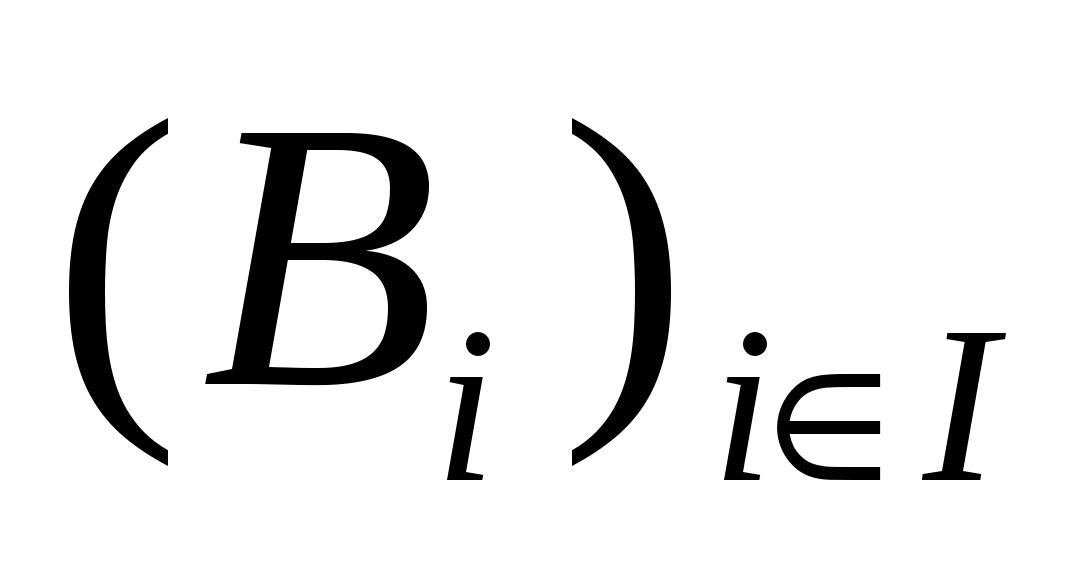 = A/R. Предположим, что существует еще одна эквивалентность Q на А такая, что Q≠ Rи = A/R. Предположим, что существует еще одна эквивалентность Q на А такая, что Q≠ Rи 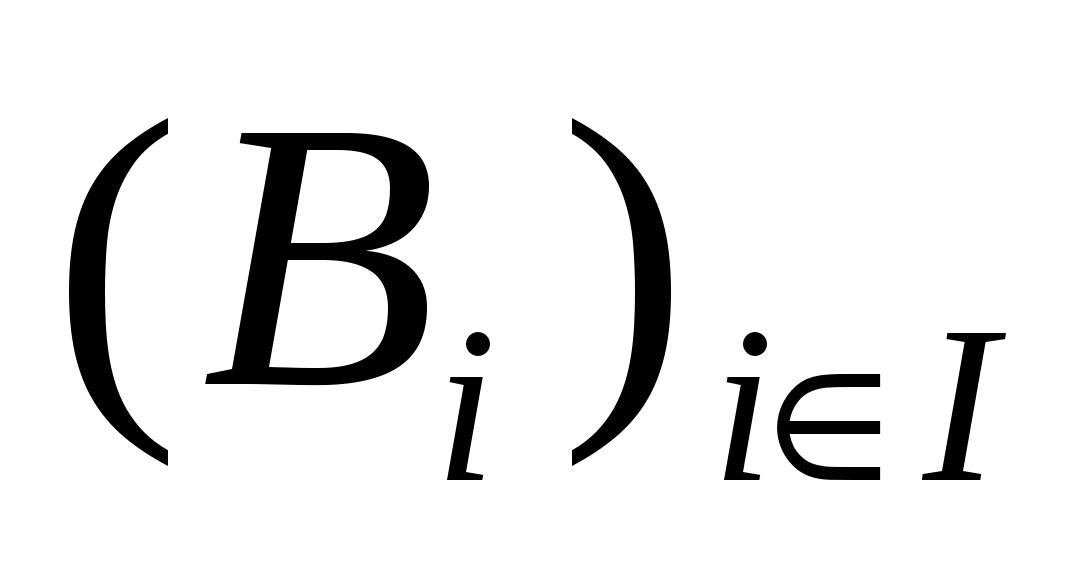 = A/Q. Однако, по условию теоремы, = A/Q. Однако, по условию теоремы, 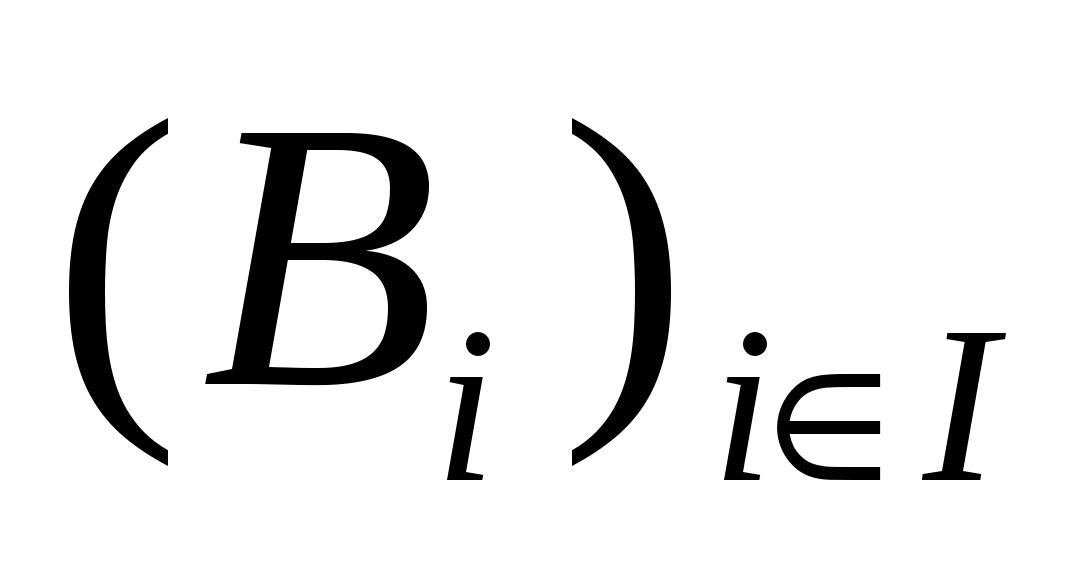 = A/R. Тогда A/R. = A/Q , что невозможно в силу п.2 теоремы 2. Следовательно, R– единственная эквивалентность на А такая, что = A/R. Тогда A/R. = A/Q , что невозможно в силу п.2 теоремы 2. Следовательно, R– единственная эквивалентность на А такая, что 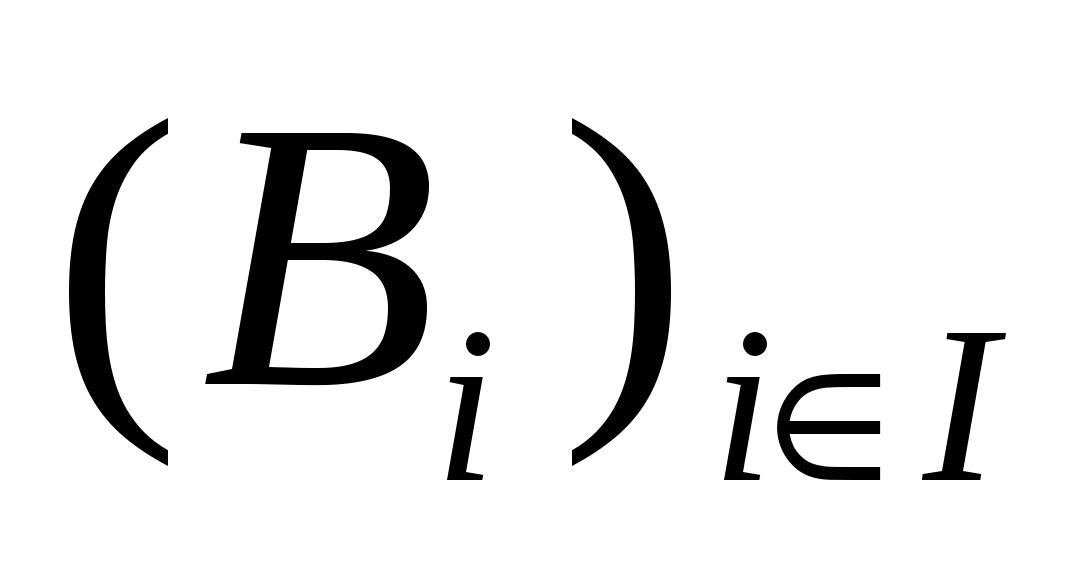 = A/R. = A/R.
П р и м е р. Указать все эквивалентности на множестве A = {1,2,3}
Разбиение множества А на классы эквивалентности
|
Соответствующая ему эквивалентность
|
А = К1U К2U К3 = {{1},{2},{3}}
|
R1 = ЕА
|
A = К1U К3 = {{1,2},{3}}
|
R2= {(1,1), (2,2), (1,2), (2,1), (3,3)}
|
A = К1 U К2 = {{1,3},{2}}
|
R3= {(1,1), (3,3), (1,3), (3,1), (2,2)}
|
A = К1U К2 = {{1},{2,3}}
|
R4 = {(1,1), (2,2), (3,3), (2,3), (3,2)}
|
A = К1 = {{1,2,3}}
|
R5= A×A
|
Проверка осуществляется так: заданы А и R , требуется определить разбиение А на классы эквивалентности, как это было в примере, приведенном выше в этом параграфе.
Мощность множества.
О п р е д е л е н и е 4. Два непустых множества называются равномощными, если существует биективное отображение одного из них на другое.
Т е о р е м а 4.Равномощность есть отношение эквивалентности на любой непустой совокупности множеств.
Обозначим символом ≈ отношение равномощности. Покажем, что оно обладает всеми свойствами отношения эквивалентности. Пусть М, М1, M2, M3- множества из данной совокупности. Так как тождественное отображение Id : М —> М есть биекция, то М ≈ М, т. е. выполнено условие рефлексивности. Пусть, далее, М1≈ М2. Тогда существует биекция f: М1→ М2 . Однако для всякой биекции существует обратная биекция f-1: М2→ M1. Таким образом. М2≈ M1, т. е. выполнено условие симметричности. Предположим теперь, что M1 ≈ M2и М2 ≈ M1Тогда существуют биекции f: М1→М2 и f: М2→M3. Их композиция f2◦f1: M1 —> Мз также является биекцией, поэтому M1 ≈ Мз, т. е. выполнено и условие транзитивности.
Используя теоремы 1 и 2, можно любую совокупность множеств разбить на попарно непересекающиеся классы эквивалентности. Тем самым вводится понятие мощности множества.
О п р е д е л е н и е 5. Мощностью множества М будем называть класс множеств, равномощных с множеством М .
Для обозначения мощности используются различные символы, например, такие: card, #. Условимся, однако, в этом пункте мощность множества М обозначать символом |М|. Основным свойством, отличающим бесконечные множества от конечных, является то, что всякое бесконечное множество равномощно некоторому его собственному подмножеству. Например, множество всех точек отрезка ОМ равномощно множеству всех точек отрезка OQ(рис. 9). Но очевидно, что 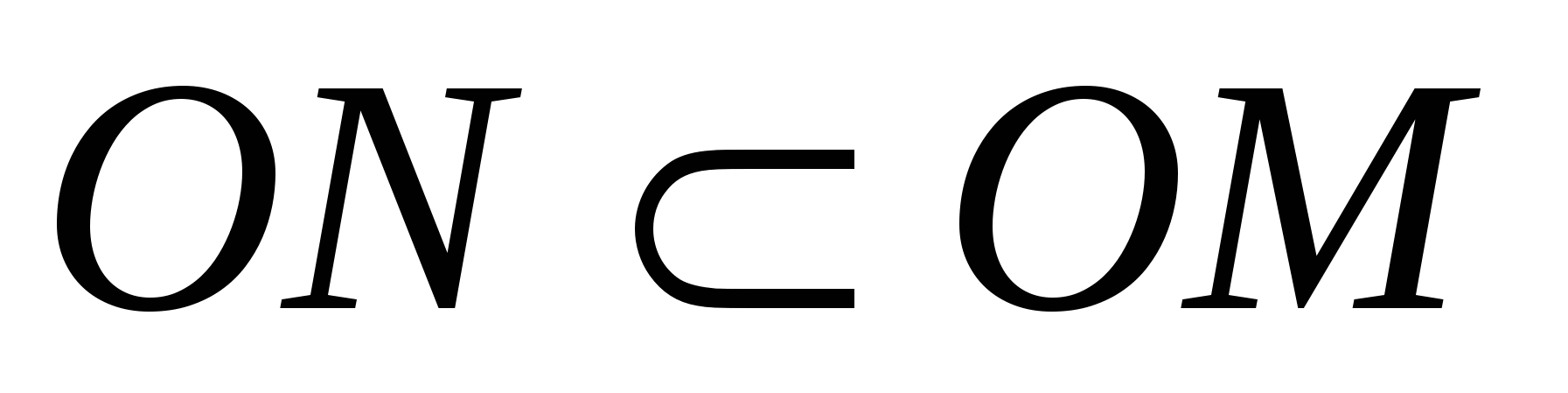 . .
О п р е д е л е н и е 6. Непустое множество М называется конечным,, если оно не равномощно никакому его собственному подмножеству.
Существует связь между тремя понятиями — отображением множества, отношением эквивалентности на множестве и разбиением множества. Любая эквивалентность определяет единственное разбиение и наоборот. Но неверно, что существует взаимно однозначное соответствие между отображениями и отношениями эквивалентности. Два разных отображения могут определять одно и то же разбиение отображаемого множества, тем самым задавая на нем одно и то же отношение эквивалентности. Так, например, любое биективное отображение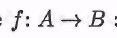 задает на А одно и то же разбиение — тривиальное разбиение на одноэлементные множества. задает на А одно и то же разбиение — тривиальное разбиение на одноэлементные множества.
следует различать общее понятие отношения эквивалентности и его частный случай — эквивалентность, или равномощность, множеств.
В обобщение этого факта определяют количественную эквивалентность, или равномощность, двух бесконечных множеств как возможность установить между ними такое соответствие.
Выражаясь формально, множество А равномощно множеству В, если существует биекция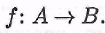 Факт равномощности множеств А и В будем записывать так: Факт равномощности множеств А и В будем записывать так: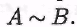
Говорят, что множество 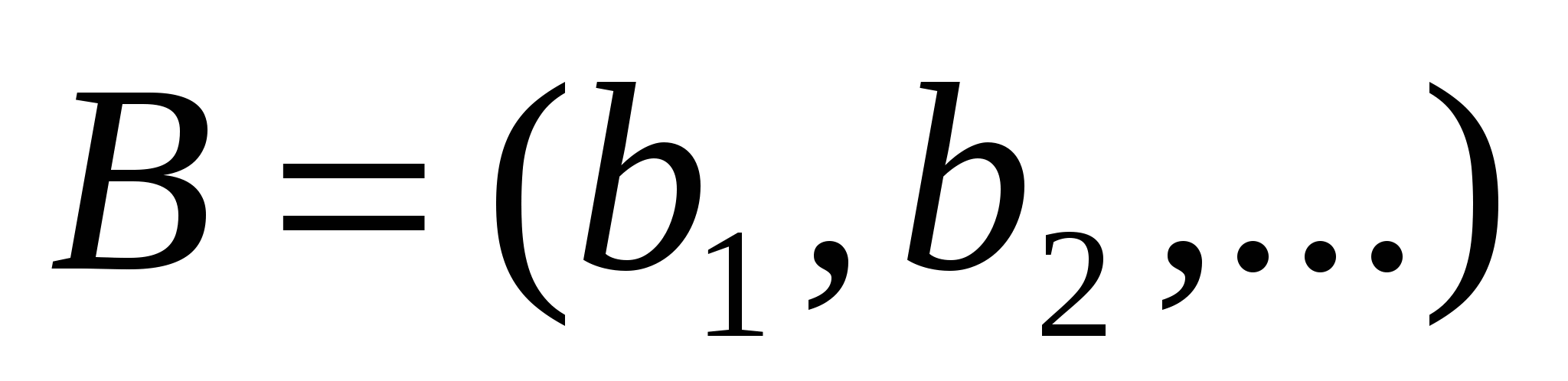 имеет ту же мощность, что и множество имеет ту же мощность, что и множество 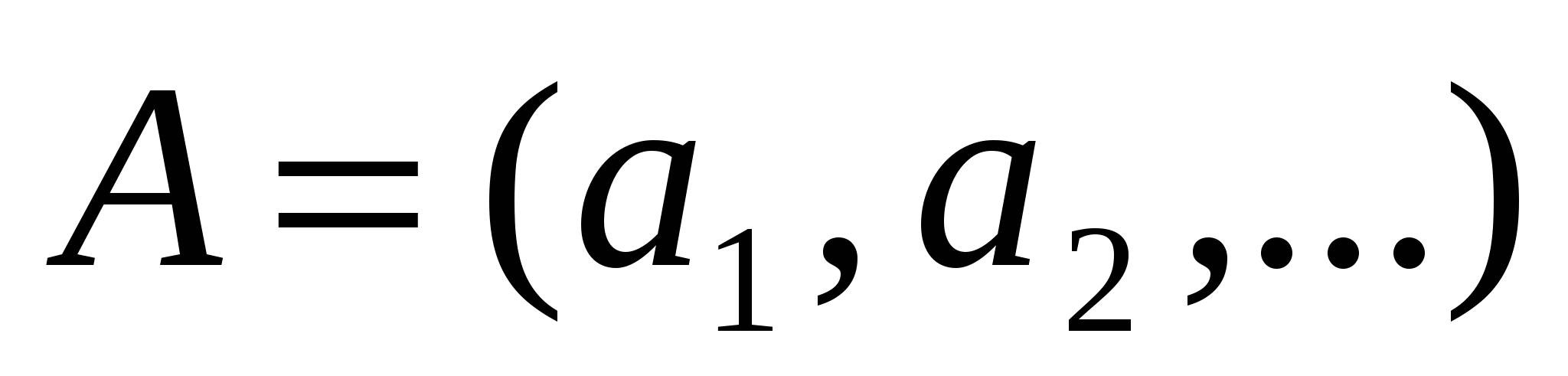 , если существует взаимно однозначное соответствие , если существует взаимно однозначное соответствие 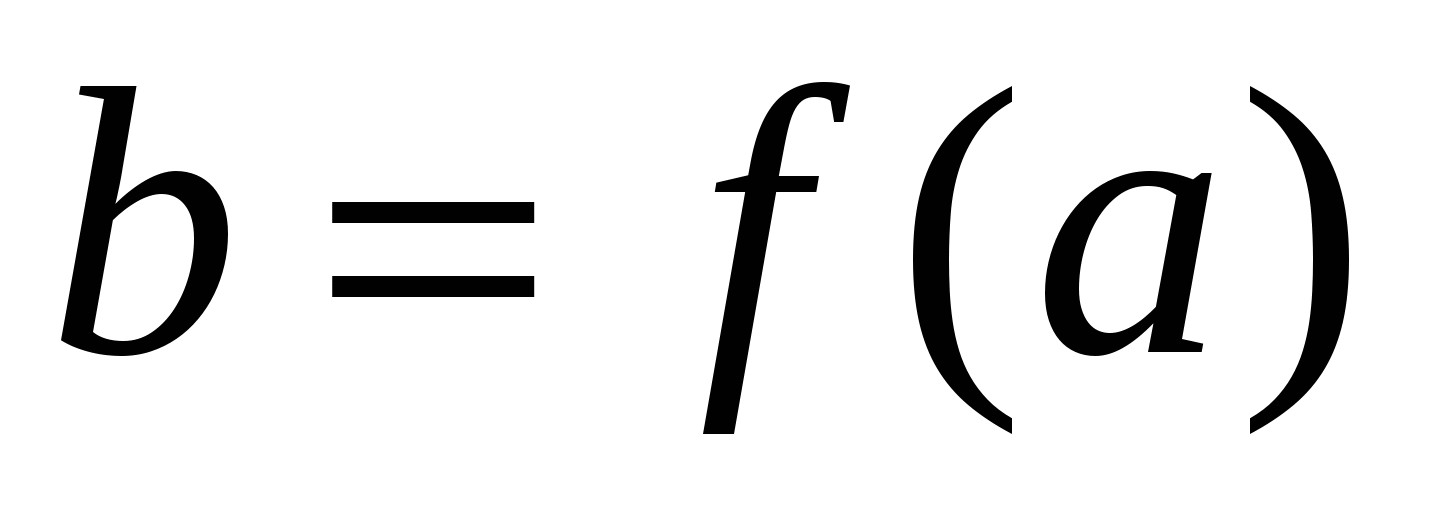 между элементами этих множеств. Можно писать между элементами этих множеств. Можно писать 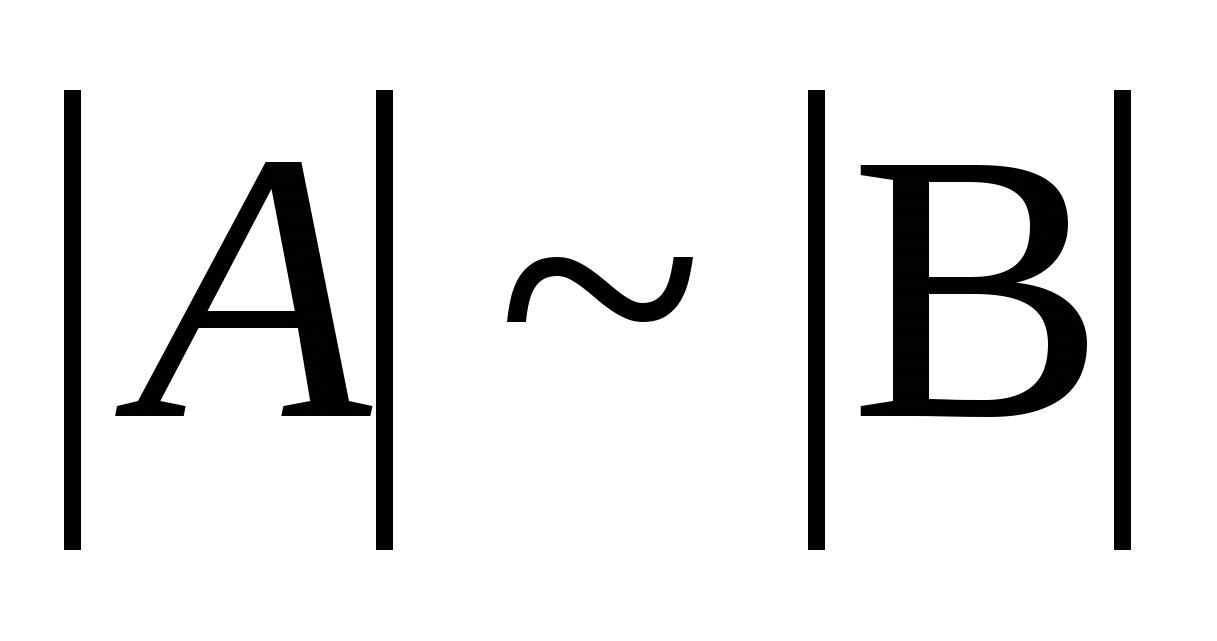 , поскольку определённое таким образом отношение есть отношение эквивалентности. (Символом , поскольку определённое таким образом отношение есть отношение эквивалентности. (Символом  обозначается мощность множества обозначается мощность множества  ). Говорят также, что ). Говорят также, что  и и 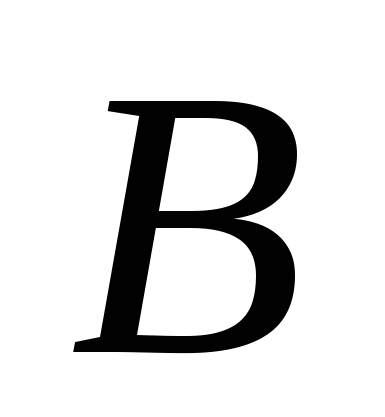 равномощны. равномощны. |
 Скачать 2 Mb.
Скачать 2 Mb.