Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов

• Название: Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов
• Дата: 08.07.2018
• Размер: 2 Mb.
• Имя файла: Lektsii_diskr_matem_konspekt.doc
• Тип: Документы; #48405
• страница: 3 из 8

П р и м е р ы:
1) D×D=D² множество точек плоскости, т.е. D² = {(a,b) : }

2) Если X₁={a;b;c;d;e;f;g;h} и X₂={1;2;3;4;5;6;7;8}, то прямое произведение этих множеств формирует 64 кортежа (x₁,x₂), однозначно определяющих каждую клетку шахматной доски, т.е. (X₁×X₂)={(a;1);(a;2);...(h;7);(h;8)}.
3) Пусть M={0,1,2,3,4,5,6,7,8,9}– множество цифр. Тогда M³ можно поставить в соответствие множество целых чисел от 0 до 999.
На основании вышеперечисленных трех основных свойств декартова произведения можно доказать следующие тождества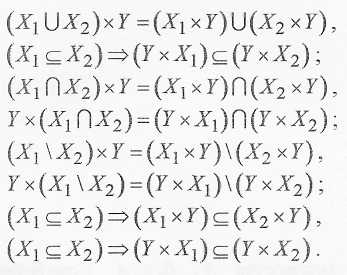


Контрольные вопросы и задачи.
I. Верно ли, что

а){1;2}{{1;2;3};{1;3};1;2};

б){1;2}{{1;2;3};{1;3};1;2};

в) если АВ и ВС, то АС;

г) если АВ и ВС, то АС;

д) если А₁А₂А₃...А_nА₁, то А₁=А₂=А₃=...=А_n

2. Перечислите элементы множества

а) Х={х|Р(х):-(х²-7х+6=0)};

б) Х={х|Р(х):-(х²-1=0)};

3. Приведите примеры таких множеств А, В, С, для которых справедливо

а) АВ, ВС, АС;

б) АВ, ВС; АС;

4. Выписать элементы множества

а) ({1;2}{2;3;4});

б) ({1;2}{3;4});

5. Найти проекции кортежей

а) Пр_2,3(х₁;х₂;х₃);

б) Пр_1,3,5(х₁;х₂;х₃;х₄;х₅);

6. Верно ли, что А=В, если

а) А={2;5;4}, B={5;4;2};

б) A={1;2;4;2}, B={1;4;2};

в) A={2;4;5}, В={2;4;3};

г) F={1;{2;5};6}, D={1;{5;2};6};

7. Приняв множество первых 20 натуральных чисел в качестве универсального множества, записать следующие его подмножества: А- множество четных чисел, В- множество нечетных чисел, С- множество квадратов чисел, D- множество простых чисел.

2. 
   Отображение множеств
   

Аналитическое понятие функции, геометрическое понятие отображения или преобразования фигуры и т. п. объединяются в общее понятие отображения одного множества в другое.

Перейдем теперь к определению отображения множеств. Пусть заданы два непустых множества X и Y.
Определение 1. Отображением множества Xв множество Y

называется правило, по которому каждому элементуставится в

соответствие единственный элемент
В математике часто отображение называют функцией и обозначают символом f. В этом случае оператор функции есть f : X Y или f : X ⁿ  Y.

Часто вместо такой записи используют запись: y=f(x), где xX, yY или

y=f(x₁; x₂;...; x_n), где (x₁; x₂;...; x_n) X ⁿ, yY, для которых элементы (х) или (x₁; x₂;...; x_n) называют аргументами функции или ее независимыми переменными, y -значением функции.

Таким образом, - это значение отображения на, элементе x.

Множество X называется областью определения отображения, а множество Y – областью значений. Будем обозначать область определения функции fчерез δ_f, область значений функции fкак ρ_f.

Если речь идет об отображении множества Х в множество Y, то это означает, что δ_f =Х и

ρ_f ⊆Y.

Следует иметь в виду, что существует также понятии отображения множества Х на множество Y. В этом случае считают, что δ_f =Х и ρ_f =Y. В остальном эти две разновидности совпадают.
П р и м е р ы.
1) В компьютере каждая буква, цифра или символ отображаются в уникальную 8-битовую кодовую комбинацию: “F”:=01000110,.. “s”:=01110011,.. ”Ф”:=11000100,.. “я”:=11001111,.. “5”:=00110101,.. “+”:=00101011,.. “”:=00100110,.. “{“:=01111011 и т.д.

2) Пусть задан в плоскости с данной на ней прямоугольной системой координат квадрат с вершинами (0; 0), (0; 1), (1; 0), (1; 1) и осуществлена проекция этого квадрата, например на ось абсцисс; эта проекция есть отображение множества Х всех точек квадрата на множество Y всех точек его основания; точке с координатами (х; у) соответствует точка (х; 0).

3) Пусть Х — множество всех действительных чисел; если для каждого действительного числа x  X положить у = f(x) = x³, то тем самым будет установлено отображение множества Х в себя.

4)Пусть Х — множество всех действительных чисел; если для каждого х  Х положить у = f(x) = arctg х, то этим будет установлено отображение множества Х на интервал ( — /2, /2).

Итак, задавая различные правила, будем получать различные отображения из Xв Y.

Множество пар отображения иногда обозначают символом F. Например,
F = {(x; y)| x X, y Y} (X×Y).

Как видим, каждое отображение однозначно определяет множество упорядоченных пар , являющееся подмножеством декартова произведения Х×Y

Проекция на первую компоненту Пр₁{(x;y)} формирует область определения Х⁰, где Х⁰Х, а на вторую компоненту Пр₂{(x;y)}- область значений Y⁰, где Y⁰Y.
П р и м е р ы.

1) Пусть X = Y – множество действительных чисел. Формула y=2x задает отображение множества X в множество Y.

2) Пусть X – множество всех треугольников на плоскости, а Y – множество действительных чисел. Сопоставляя треугольнику его площадь, получаем отображение первого множества во второе.

3) Пусть X = {1, 2, 3}, Y = {2, 3, 4}. Множество пар

F = {(1, 2), (2, 2), (3, 3)}

задает отображение f, при котором f(1)=f(2)=2, f(3)=3.

Функция fназывается 1-1 функцией, если для любых х₁, х₂, yиз того, что y = f(x₁) иy = f(x₂) следует х₁ = х₂.
П р и м е р ы.

1) Функция y = sin x является 1-1 функцией, если,и не является 1-1 функцией, если ее рассматривать на всей вещественной оси.

2) Функция, которая каждому человеку ставит в соответствие его дату рождения, не является 1-1функцией.

Функцияосуществляет взаимно-однозначное соответствие между А и В, если

и f- 1-1 функция.

П р и м е р.

1) Функция, которая ставит в соответствие каждому студенту данного ВУЗа его номер студенческого билета, осуществляет взаимнооднозначное соответствие между множеством студентов данного ВУЗа и множеством номеров студенческих билетов, выданных на данный момент времени.

2) Функция у= ехр(х), заданная на множестве действительных чисел, осуществляет взаимно-однозначное соответствие между ее областью определения и областью значений.

Отображение вида f: X×Y→Z называют функцией двух переменных и пишут z= f(x,y). Аналогично определяются функции большего числа переменных. Так, для отображения, область определения которого задана прямым произведением Хⁿ, множество пар отображения и оператор отображения имеют следующий вид:

F={(x₁; x₂;...; x_n; y)| x_i X; y Y} Xⁿ  Y,

f: ХⁿY или y=f((x₁; x₂;...; x_n).
Композиция (произведение) отображений.
Для двух отображений f₁:XZ и f₂:ZYможно найти их композицию, т.е. сформировать новое отображение f=(f_1f₂): XY,при условии, что элементы области значений первого отображение есть элементы области определения второго отображения.

Композиция f_1f₂ определяется как отображение из X в Y, задаваемое формулой y =f₂(f₁(x)). Тем самым задается график отображения f_1f₂, т.е. множество упорядоченных пар (x,y), таких, что y =f₂(f₁(x)). Таким образом, график композиции отображенийf₁ и f₂ есть

f_1f₂ = и

Отметим, что при построении композиции отображений обычно предполагают, что пересечение области значений отображения f₁ и области определения отображения f₂не пусто (ρ_f1∩ δ_f2 ≠ ∅), поскольку в противном случае композиция была бы пуста.

Полезно отметить также, что если f₁ и f₂биекции, то и композиция их также будет биекцией.

Например, если отображения f₁,f₂ множества действительных чисел в себя заданы формулами

z = f₁(x)= x+1, y = f₂ (z)=2z,

то

(f_1 f₂)(x)=f₂(f₁(x))=f₂(x+1)=2(x+1);

(f_2 f₁)(x)=f₁(f₂(x))=f₁(2x)=2x+1.

Из этого примера видно что операция композиции не коммутативна.
Элемент у = f(x), который отображением f сопоставляется элементу хX называется образом эле­мента х при отображении f. В общем случае для отображения f : X → Y может существовать несколько различных элементов множества Х, образы которых совпадают. Множество всех элементов хX , для которых f(x)= a называют прообразом элемента при отображении f .

Например, прообраз числа |а|≤ 1 при отображении y = sinxесть множество .

Прообраз элемента может быть пустым множеством. Это имеет место, например, для числа 2 при отображении y = sinx.

Множество всех , таких, что найдется , для которого y = f(x), называют областью значений отображения f.
Виды отображений.
Отображение f : X → Y называется инъективным (инъекцией), если каждый элемент из области его значений имеет единственный прообраз, т.е. из f(x₁) = f(x₂) следует x₁ = x₂, или, что то же самое если образы различных элементов также различны, то есть f(x) ≠ f(y) при x ≠ y.
Отображение f : X → Y называется сюръективным (сюръекцией), если его область значений совпадает со всем множеством Y, или иначе говоря если всякий элемент y из Y является образом некоторого элемента x из X, то есть f(X)=Y.

Отображение f : X → Y называется биективным (биекцией), если оно одновременно инъективно и сюръективно.
Таким образом, отображение f:X→Yназывается биекцией, если оно :

1. 
   Переводит разные элементы множества X в разные элементы множества Y(инъективность).
   
2. 
   Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами, .
   

Биекцию также называют взаимно-однозначным отображением. Множества, для которых существует биекция называются равномощными.
П р и м е р ы.
1) f(x) = xи f(x) = x³ - биективные функции из Rв себя.

2) Отображение, заданное равенством v(n) = = п + 1, есть, как нетрудно показать, биекция множества нату­ральных чисел N на его подмножество

3) Отображениеесть биекция множества всех натуральных чисел на множество всех четных натуральных чисел.

4) Любая показательная функция, есть биекция множества R всех действительных чисел на множествовсех положительных действительных чисел. Но если ее рассматривать как функцию в R, то она уже не будет биективной ( у отрицательных чисел не будет

прообразов ).

5) Функцияесть биекция множества R на интер­вал

6) Отображение f:R→R≥0, f(x)=x2, множества всех действительных R на множество неотрицательных чисел R≥0 сюръективно, но не инъективно, и поэтому не является биективным.
С в о й с т в а.

1) Функция f:X→Yявляется биективной тогда и только тогда, когда существует обратная функцияg:Y→Xтакая, что и f(g(y))=y.

2) Если композиция функций f◦gбиективна, то и сами функции f и g

биективны.

3) Композиция биекций является биекцией.

П р и м е р.
Функция f:R→R>0, f(x)=ex, устанавливает взаимно однозначное соответствие множества всех действительных чисел R с множеством положительных действительных чисел R>0. Обратным к отображению f является отображение g:R>0→R, g(x)=ln x.