|
|
Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов
Теорема. Для любого отношения эквивалентности на множестве А множество классов эквивалентности образует разбиение множества А. Обратно, любое разбиение множества А задает на нем отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения.
Теорема, приведенная выше, позволяет отождествлять отношения эквивалентности и разбиения: любая эквивалентность определяет единственное разбиение и наоборот.
5.2. Мощность множеств.
Из определения равномощности и свойств биекции также следует, что для любого множества А имеет место А
А (тождественное отображение есть биекция множества А на себя); а для любых множеств А, В, С из А
В и В
С следует А
С (композиция биекций есть биекция).
Таким образом, отношение равномощности множеств есть отношение эквивалентности, заданное на „множестве всех множеств" (на самом деле на множестве всех подмножеств некоторого универсального множества).
Если мы обозначим через |A| класс эквивалентности множества А по отношению
, то утверждение о равномощности множеств А и В можно записать так: |A| = |B|.
Этот класс эквивалентности |A| называют мощностью множества А.
Перейдем теперь к исследованию мощности бесконечных множеств. Таковы хорошо известные нам числовые множества N, Z,Q,R и С.
Любое множество, равномощное множеству всех натуральных чисел, называют счетным. Мощность счетного множества обозначают N0(читается „алеф нуль").
Любую биекцию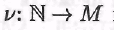 называют нумерацией счетного множества М; если элемент М есть называют нумерацией счетного множества М; если элемент М есть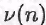 для некоторого для некоторого 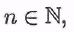 то этот элемент М обозначаем через то этот элемент М обозначаем через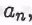 называя натуральное число п номером элемента апотносительно данной нумерации v. называя натуральное число п номером элемента апотносительно данной нумерации v.
П р и м е р.
А). Множество всех нечетных натуральных чисел счетно. Нумерацию vможно задать так: ν (n) = 2n -1, 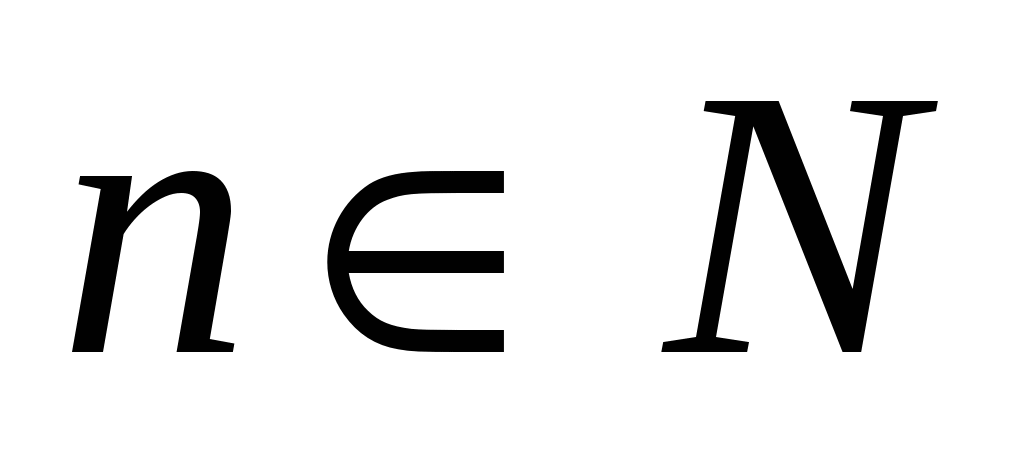
Б). Множество всех натуральных чисел, делящихся на заданное число 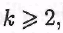 счетно. Нумерацию счетно. Нумерацию 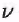 можно задать так: можно задать так: 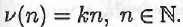 В частности, при В частности, при 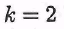 получаем, что мно- получаем, что мно-
жество всех четных чисел счетно. Этот и предыдущий примеры показывают, что бесконечное (счетное) множество может иметь собственное равномощное ему подмножество.
В). Множество Z всех целых чисел счетно. Нумерацию можно установить так:
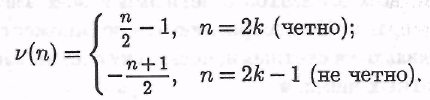
Рассмотрим свойства счетных множеств.
Т е о р е м а. Любое бесконечное множество содержит счетное подмножество.
Пусть M0— бесконечное множество. Значит, оно не пусто и существует элемент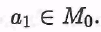 Положим Положим 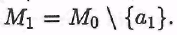
Множество M1не пусто, так как в противном случае имело бы место равенство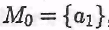 , что противоречит предположению о бесконечности M0. Выберем элемент , что противоречит предположению о бесконечности M0. Выберем элемент 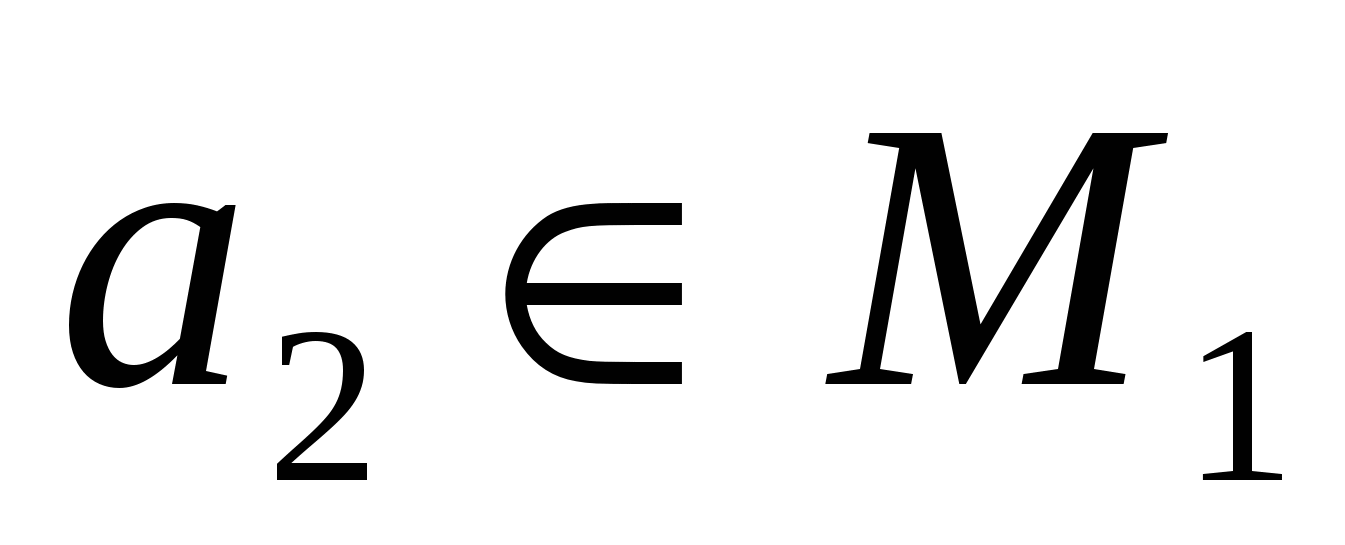 и положим и положим
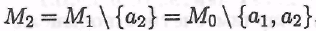 . Множество M2также не пусто, поскольку иначе мы бы имели . Множество M2также не пусто, поскольку иначе мы бы имели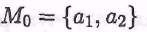 и множество M0 было бы конечным. и множество M0 было бы конечным. |
|
|
 Скачать 2 Mb.
Скачать 2 Mb.