Главная страница
Навигация по странице:

  • Росморфлот Новороссийская государственная морская академия

  • 1. Расчёт плавания судна по ДБК

  • 1.2 Расчёт плавания судна по ДБК по основным формулам

  • 1.3 Расчёт плавания судна по ДБК через параметры её пересечения с экватором

  • 1.4 Расчёт плавания судна по ДБК по координатам вертекса

    		•

    Курсовая по мос. Курсовая работа по дисциплине "Математические основы судовождения " Вариант мос 137


    Скачать 387 Kb.
    НазваниеКурсовая работа по дисциплине "Математические основы судовождения " Вариант мос 137
    АнкорКурсовая по мос
    Дата18.12.2022
    Размер387 Kb.
    Формат файлаdoc
    Имя файлаkursovik po mosu.doc
    ТипКурсовая
    #850477
    страница1 из 5
      1   2   3   4   5

    МИНИСТЕРСтВО транспорта РоссиЙСКОЙ ФЕДЕРАЦИИ


    Росморфлот

    Новороссийская государственная

    морская академия

    Специальность

    "Судовождение на морских путях"



    Курсовая работа


    по дисциплине

    "Математические основы судовождения"



    Вариант МОС – № 137

    "Аналитический расчет координат

    места судна при избыточном числе измерений"



    Выполнил: к-т 137 группы


    Кириллин К.В.

    Рецензент: профессор, д.т.н. Васьков А. С.
    г. СПб

    2005 г.

    1. Расчёт плавания судна по ДБК
    1.1 Оценка целесообразности плавания судна по ДБК
    Преимущества плавания по ДБК оценивается абсолютной или относительной разностью расстояний по ортодромии и локсодромии между пунктами отхода и прихода с помощью табл. 23-б МТ-75 или выражений:

      кн) / 2 = (31º18,2’- 19º54,4’) / 2 = 5º41.9’

    S% = 100% (Sорт - Sлок) / Sорт

    S% =  = 0.161643504 %

    где S% - относительная разность расстояний между пунктами отхода и прихода по локсодромии и ортодромии;

     угол сферического схождения меридианов;

    ортодромическая поправка;

    Sорт , Sлок - расстояния по ортодромии и локсодромии между пунктами;

    н , к - направления ортодромии в начальной и конечной точках (см. п. 1.2.1).
    1.2 Расчёт плавания судна по ДБК по основным формулам

    1.2.1 Задание ДБК по координатам пунктов отхода и прихода
    Задание ДБК сводится к решению сферического навигационного треугольника АPNB рис. 2., заданного координатами пунктов отхода А(н= 7º40.8’S н = 34º20.9’W) и прихода B(к= 49º30.5’N к = 6º45.3’W), по основным формулам (косинуса стороны и котангенсов) и определению направлений ортодромии (курс) в начальной (н) и конечной к) точках её длины (Sорт)

    ctgKн = cosн tgк cosecsinн ctg2.764572950

    Kн = 19º54.4’

    K’ = 19º54.4’

    ctgKк =  tgн cosк cosecsinк ctg1.646601401

    Kк = 31º18.2’

    K’= 19º54.4’

    cos Sорт = sinн sinк + cosн cosк cos = 0.469153757

    Sорт = 60 * 62.02º = 3721.237255 (миль)

    –
    к
    6º45.3’W

    н
    34º20.9’W




    
    27º33.6’к E



    K - Значение курса в круговом счёте

    K’ - Значение курса в четвертном счёте
    Решения этих формул может выполняться с помощью таблиц логарифмов МТ-75, микрокалькуляторов или ЭВМ. В данной работе расчёт выполнен с помощью ЭВМ.


    1.2.2 Расчёт промежуточных точек ДБК и курсов между ними.
    Для нанесения ДБК на карту и плавания по ней определяются координаты промежуточных точек:

    tgi = tgн cos(i - н) + ctgKн secн sin(i - н)

    где i - широта промежуточной точки ДБК;

    i - долгота промежуточной точки ДБК, задаётся значениями проведённых меридианов на генеральной карте (через 50, 100,...)

    Разность долгот между промежуточными точками ДБК задаётся из условия, чтобы разность длин ортодромии и локсодромии между этими точками не превышали заданных значений (в данной курсовой работе - 1 миля). С помощью таблицы 23-б МТ-75 обнаруживаем, что 50 - достаточно.

    Направление и длина локсодромии между промежуточными точками ДБК определяется из локсодромического треугольника, образованного локсодромией, меридианами и параллелями этих точек рис. 1, по выражениям: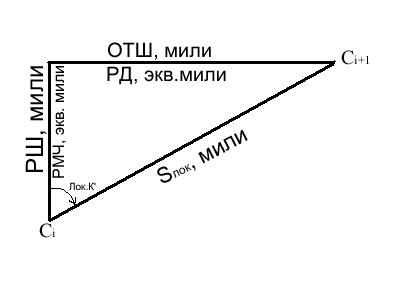




    Рис. 1. Локсодромический треугольник для промежуточных точек ДБК.
    tgЛок.Кi = РДi/РМЧi или tgЛок.Кi = ОТШi/РШi ;

    Sлокi = РШi secЛок.Ki или Sлокi = (РШ2 + ОТШ2)0,5

    РДi = i+1 - i; РШi = i+1 - i; ОТШ = РДi cosсрi; срi = (i+1 + i)/2
    Результаты расчётов представляются в форме таблицы:

    Таблица 1.1

    № точки
    i
    i - н
    i
    РДi
    РШi
    ОТШi
    Лок Кi
    Sлокi

    0
    3420.9’W
    0 00’
    740,8’S
    260.1’
    722.13’
    243.00’
    18.6
    762.0’

    1
    3000’W
    420.9’ к Е
    423.3’N
    300’
    799.53’
    267.27’
    18.5
    843.4’

    2
    2500’W
    920.9’ к Е
    1743.1’N
    300’
    691.31’
    248.52’
    19.9
    735.3’

    3
    2000’W
    1420.9’к Е
    2914.5’N
    300’
    556.40’
    231.56’
    22.6
    603.1’

    4
    1500’W
    1920.9’к Е
    3831.0’N
    300’
    433.00’
    215.47’
    26.5
    483.9’

    5
    1000’W
    2420.9’к Е
    4544.0’N
    195’
    131.45’
    131.25’
    30.1
    262.1’

    6
    645.3’E
    2733.6’к Е
    4930.5’N
















    -
    -
    -
    1655.1’
    3430.02’
    1339.30’
    -
    3689.8’

    1.3 Расчёт плавания судна по ДБК через параметры её пересечения с экватором

    1.3.1 Определение параметров пересечения ДБК с экватором
    Параметры пересечения ДБК с экватором определяются по формулам:
    tg(ср  tg(sin(2ср) cosec0.194520438

    ср - = 1100.7’W

    ср = 2033.1’W

    0 = 3133.8’W

    ctgK0 = tgн cosec(н - 0) = 0,358476035

    н - 0 = 247.1’ к W K0 = 19.72

    ср = (н + к)/2 = 2054.9’N ср = (н + к)/2 = 2033.1’W


    –
    к
    49º30.5’N

    н
    7º40.8’S




    
    57º11.3’ к N


    где долгота первой точки пересечения с экватором;

    Долгота пересечения ДБК с экватором может быть определена также через найденный по формуле начальный курс:

    Проверка: tg(н - 0) = tgKн sinн

    0 = 3420.9’ - 247.1’ = 3133.8’W – верно.
    1.3.2 Расчёт промежуточных точек ДБК и курсов между ними
    Широты промежуточных точек ДБК определяются с помощью формулы:

    tgi = sin(i - 0) ctgK0
    Результаты расчетов представляются в форме таблицы

    Таблица 1.2

    № точки
    i
    i - 0
    i
    РДi
    РШi
    ОТШi
    Лок Кi
    Sлокi

    0
    3420.9’W
    247.1’W

    740.8’S
    250.1’
    722.2’
    243.0’
    18.6
    762.0’

    1
    3000’W
    134.1’E
    422.1’N
    300’
    799.9’
    267.5’
    18.5
    843.4’

    2
    2500’W
    634.1’E
    1741.9’N
    300’
    691.5’
    249.9’
    19.9
    735.3’

    3
    2000’W
    1134.1’E
    2913.5’N
    300’
    556.7’
    231.9’
    22.6
    603.1’

    4
    1500’W
    1634.1’E
    3830.2’N
    300’
    226.8’
    215.8’
    26.5
    483.9’

    5
    1000’W
    2134.1’E
    4543.3’N
    195’
    365.9’
    131.4’
    30.1
    262.1’

    6
    645.3’W
    2421.5’E
    4930,5’N
    600’
    - 268.4’











    -
    -
    -
    1650.1’
    3430.2’
    1339.5’
    -
    3689.8’

    1.4 Расчёт плавания судна по ДБК по координатам вертекса

    1.4.1 Вычисление координат вертекса
    Координаты точки вертекса определяются по формулам:
    tg(v - ср) = ctg(sincosec(2ср) = 5.138359318

    = 57º11.3’ к N

     = 27º33.6’ к E

    ср = 2054.9’N

    v - ср = 78º59.2’ к E

    v = 58º26.1’E
    tgv = tgн sec(н - v) = 2.781122105

    v = 7016.7’N
    Координаты точки вертекса могут быть также определены по формулам:

    Проверка : v = 90º00’ - K0

    v = 7016.7’N – верно
    v = 0 + 90º00’

    v = 58º26.1’E

    1.4.2 Расчёт промежуточных точек ДБК и курсов для плавания судна
    Широты промежуточных точек ДБК определяются с помощью формулы:
    tgi = tgv cos(i - v)
    Результаты расчетов представляются в форме таблицы

    Таблица 1.3

    № точки
    i
    i - v
    i
    РДi
    РШi
    ОТШi
    Лок Кi
    Sлокi

    0
    3420.9’W
    9246.0’W

    748.8’S
    250.1’
    722.2’
    243.0’
    18,6
    762,1

    1
    3000.0’W
    8825.8’W
    422.1’N
    300’
    799.9’
    267.5’
    18,5
    843,4

    2
    2500.0’W
    8325.8’W
    1742.0’N
    300’
    691.5’
    249.9’
    19,9
    735,3

    3
    2000.0’W
    7825.8’W
    2913.5’N
    300’
    556.7’
    231.9’
    22,6
    603,0

    4
    1500.0’W
    7325.8’W
    3830.2’N
    300’
    226.8’
    215.8’
    26,5
    483,9

    5
    1000.0’W
    6825.8’W
    4543.3’N
    195’
    365.9’
    131.4’
    30,1
    262,1

    6
    645.3’W
    6510.9’W

    4930.5’N

















    -
    -
    -
    1650.1’
    3430.2’
    1339.5’
    -
    3689,8

      1   2   3   4   5

    написать администратору сайта