Курсовая работы по дисциплине Системы автоматического управления электроприводом. КР, гр. ЭГП-16-1, Патрушев В. А.. Курсовой проект по дисциплине Электротехнические комплексы и системы преобразования электроэнергии
 Скачать 1.92 Mb. Скачать 1.92 Mb.
|
3.2 Анализ переходных процессов в системе векторного управления методом имитационного моделированияНа рисунке 3.1 представлена модель, в которой при моделировании регулятором скорости является П-регулятор. Результаты моделирования для ПИ-регулятора потокосцепления представлены на рисунке 3.2. На рисунке 3.3 представлены результаты моделирования П-регулятора скорости. 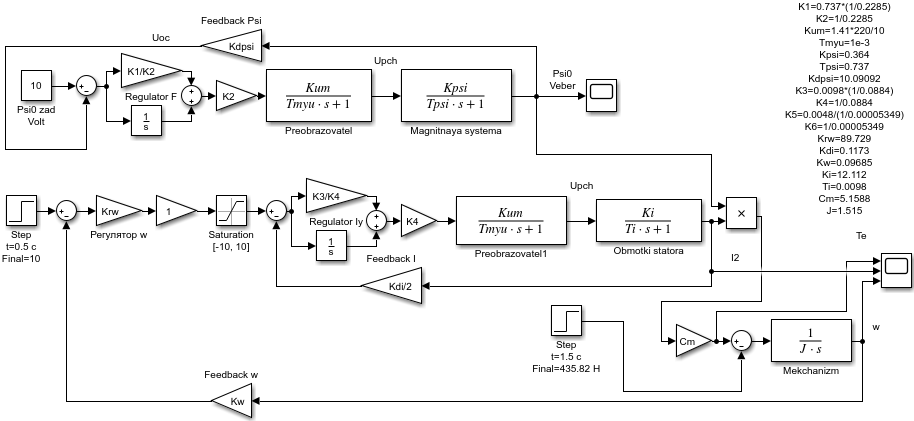 Рисунок 3.1 – Модель с П-регулятором скорости Результат моделирования ПИ-регулятора потокосцепления (рисунок 3.2) показывает, что главное потокосцепление соответствует рассчитанному, которое равно: 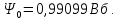 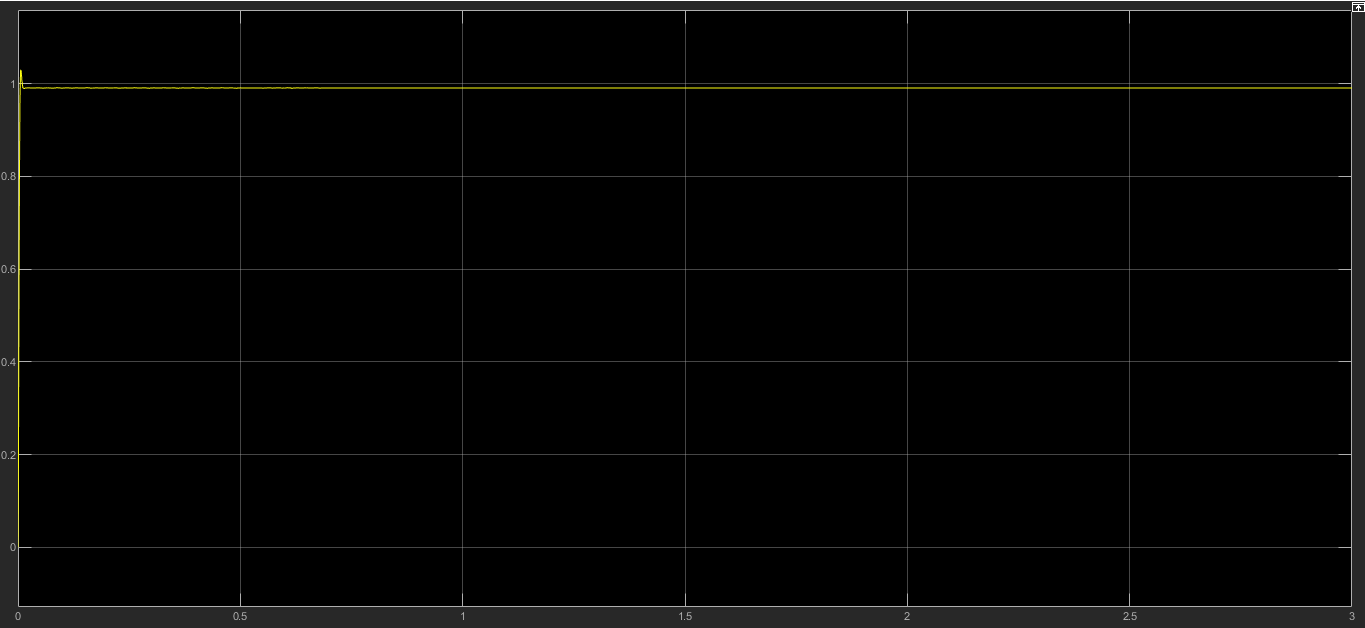 Рисунок 3.2 – ПИ-регулятор потокосцепления 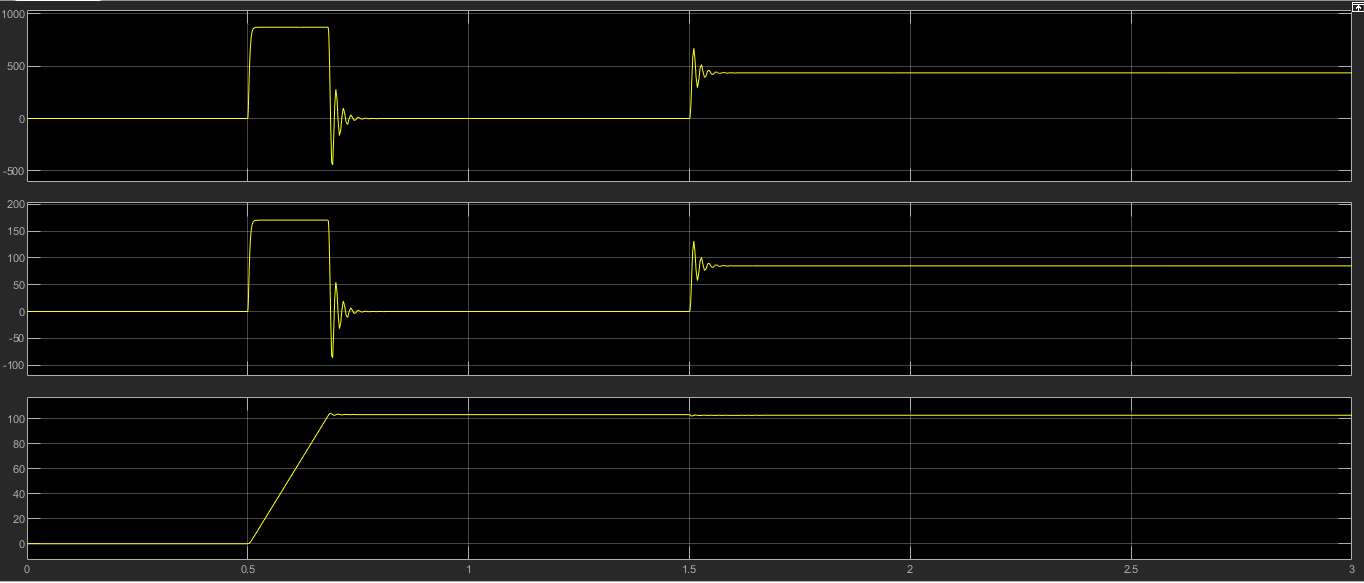 Рисунок 3.3 – Графики, сверху вниз: момент, ток и угловая скорость вращения вала (при использовании П-регулятора скорости) На графиках можно наблюдать (рисунок 3.3), что установившиеся значения момента, тока, угловой скорости вращения вала двигателя соответствуют номинальным значениям, то есть: 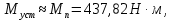 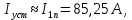 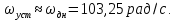 Далее произвожу моделирование при регулировании скорости при помощи ПИ-регулятора. Модель представлена на рисунке 3.4. Результаты настройки ПИ-регулятора скорости на технический и на симметричный оптимумы представлены на рисунках 3.5 и 3.6 соответственно. По графикам видно, что значения не устанавливаются, такой результат обусловлен большой величиной коэффициентов 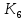 и и 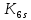 . Рассчитанные коэффициенты ПИ-регулятора скорости требуют коррекции. . Рассчитанные коэффициенты ПИ-регулятора скорости требуют коррекции.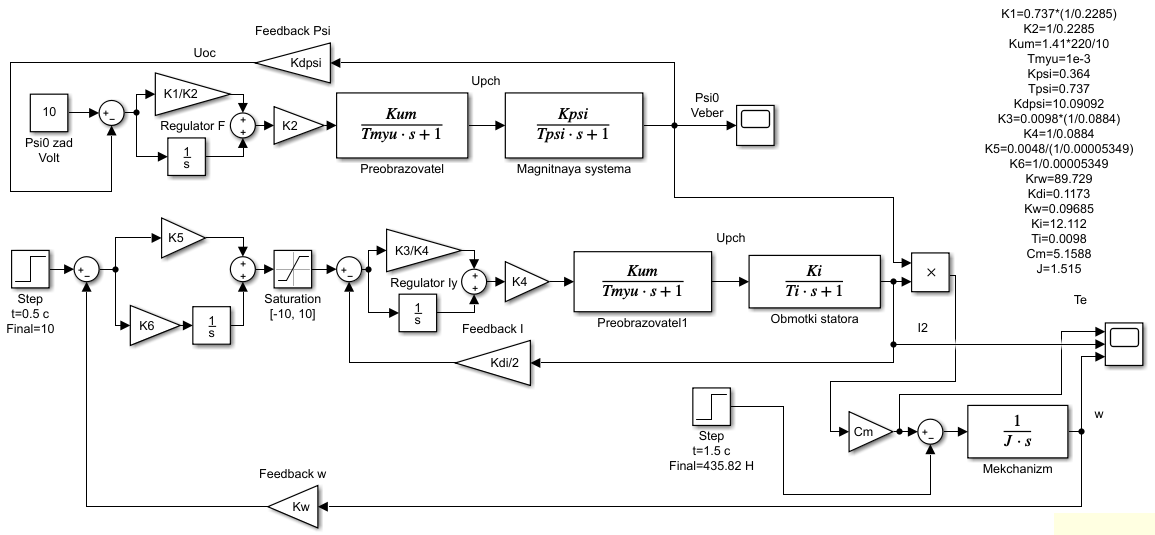 Рисунок 3.4 – Модель с ПИ-регулятором скорости 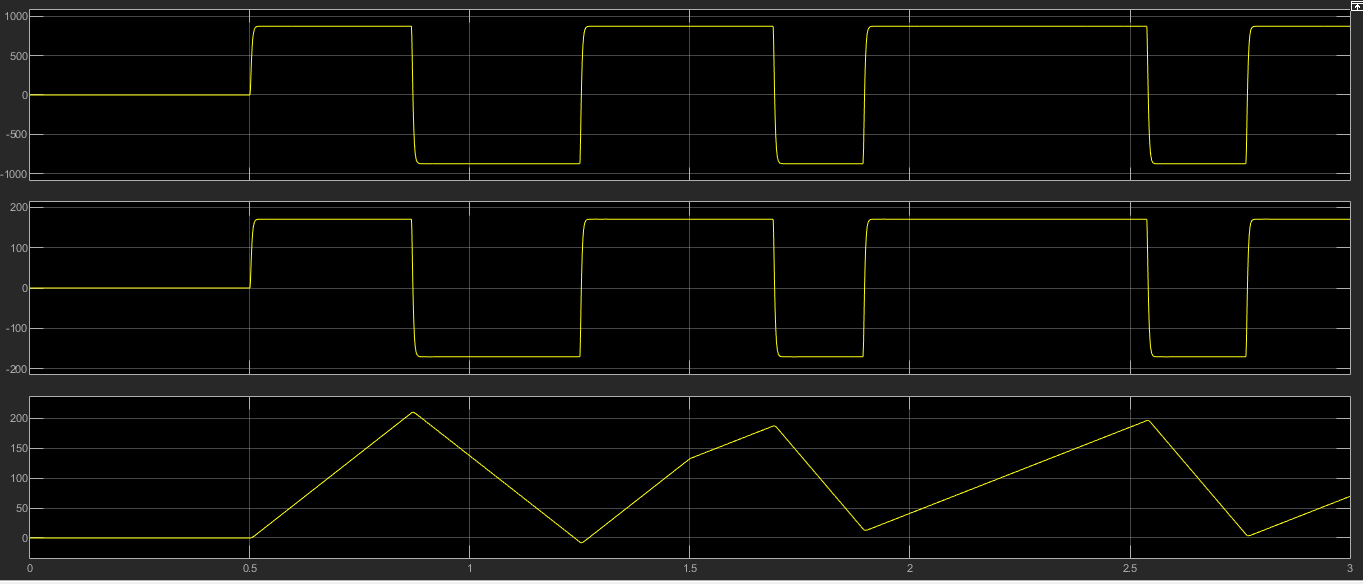 Рисунок 3.5 – Графики, сверху вниз: момент, ток и угловая скорость вращения вала (настройка ПИ-регулятора скорости на технический оптимум) 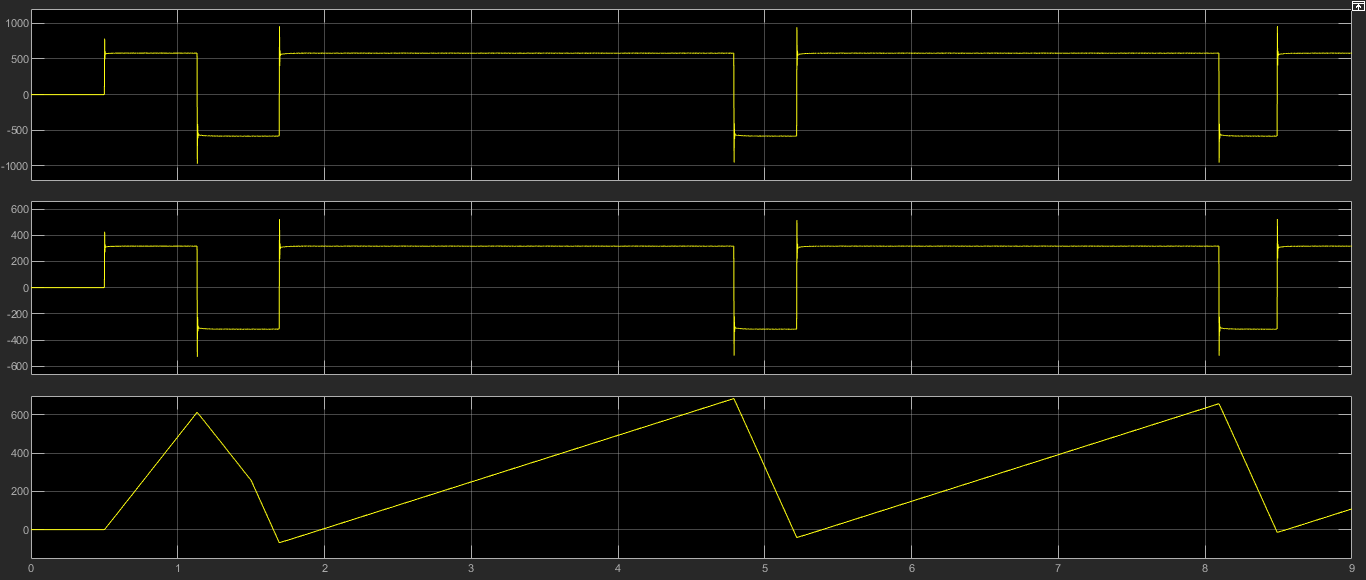 Рисунок 3.5 – Графики, сверху вниз: момент, ток и угловая скорость вращения вала (настройка ПИ-регулятора скорости на симметричный оптимум) В таком случае я прибегну к корректировке этих коэффициентов по методу Зиглера – Никольса [3]: 1) перевожу регулятор в режим пропорционального регулирования; 2) в этом режиме увеличиваю коэффициент 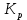 = = 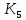 до возникновения незатухающих колебаний, в моём случае до возникновения незатухающих колебаний, в моём случае 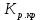 = 199,4 (графики при этом коэффициенте представлены на рисунке 3.7); = 199,4 (графики при этом коэффициенте представлены на рисунке 3.7);3) в этом состоянии системы фиксирую период колебаний 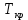 = 1/ = 1/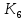 , в моём случае , в моём случае 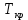 = 0,012 с. = 0,012 с.4) вычисляю скорректированные значения коэффициентов 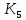 и и 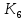 : :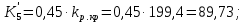 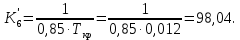 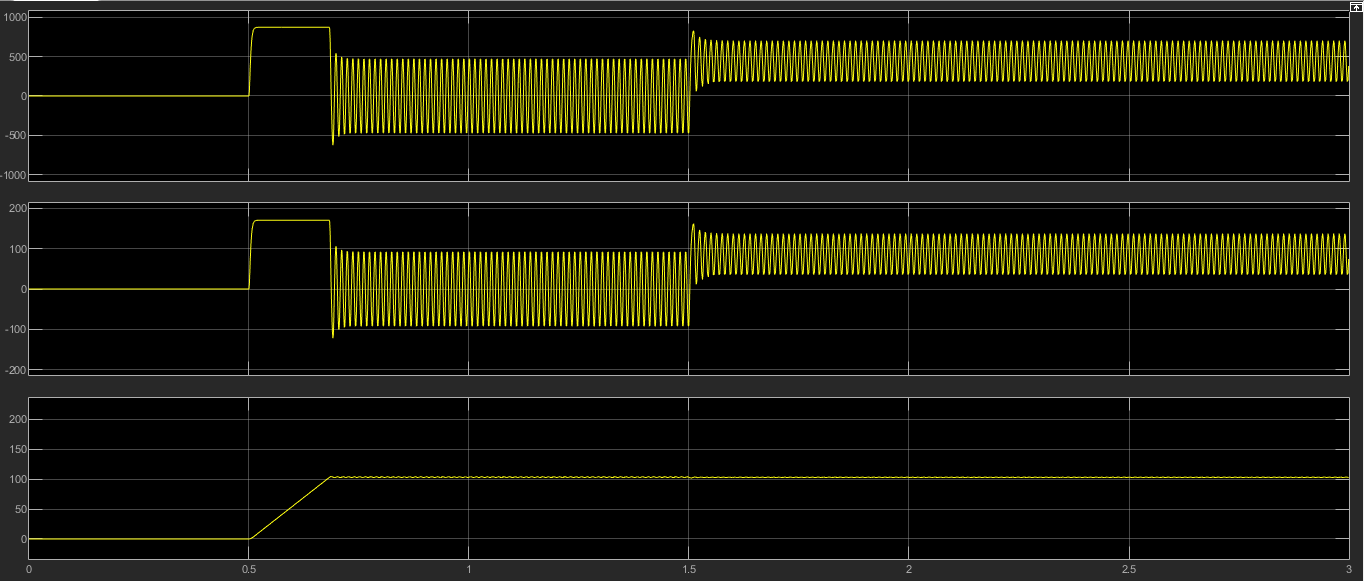 Рисунок 3.7 – Графики, сверху вниз: момент, ток и угловая скорость вращения вала (при состоянии незатухающих колебаний) Произведя корректировку коэффициентов 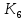 провожу моделирование и получаю графики, представленные на рисунке 3.8. провожу моделирование и получаю графики, представленные на рисунке 3.8.Так как 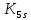 численно равен коэффициенту численно равен коэффициенту 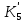 , то корректировка коэффициента , то корректировка коэффициента 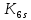 приведёт к его равенству с исправленным коэффициентом приведёт к его равенству с исправленным коэффициентом 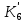 , а это значит, что все расчёты и графики переходных процессов будут аналогичны. , а это значит, что все расчёты и графики переходных процессов будут аналогичны.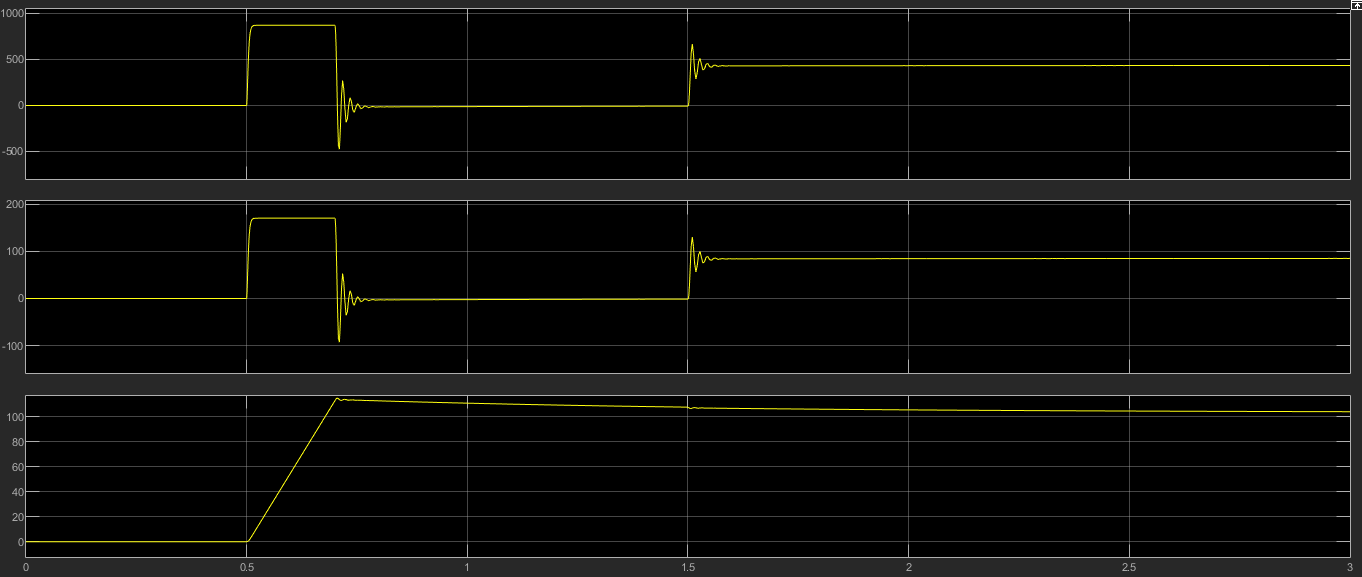 Рисунок 3.8 – Графики, сверху вниз: момент, ток и угловая скорость вращения вала (при скорректированных значениях коэффициентов ПИ-регулятора скорости) Графики, полученные в результате моделирования системы со скорректированным ПИ-регулятором скорости, показывают, что установившиеся значения момента, тока, угловой скорости вращения вала двигателя соответствуют рассчитанным номинальным значениям, а именно: 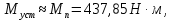 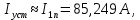 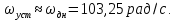 Заключение по разделу Произведя моделирование, я могу сказать, что коэффициенты П-регулятора скорости и ПИ-регулятора потока, получаемые расчётным путём, позволяют получить номинальные значения характеристик электродвигателя, коэффициенты же ПИ-регулятора скорости требуют корректировки, то есть настройки ПИ-регулятора скорости в ходе моделирования. |
