Курсовая работы по дисциплине Системы автоматического управления электроприводом. КР, гр. ЭГП-16-1, Патрушев В. А.. Курсовой проект по дисциплине Электротехнические комплексы и системы преобразования электроэнергии
 Скачать 1.92 Mb. Скачать 1.92 Mb.
|
6 Цифровые системы управления6.1 Модели цифрового фильтра первого порядка6.1.1 Общие сведения о цифровых системах управленияЦифровые, или дискретные, системы управления имеют в своем составе устройства преобразования аналоговых сигналов в дискретные (аналого-цифровые преобразователи, или АЦП) и устройства обратного преобразования (цифро-аналоговые преобразователи, или ЦАП) (рисунок 6.1) [4]. 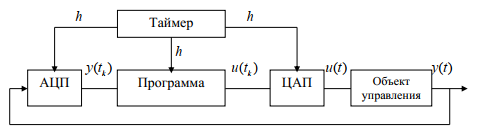 Рисунок 6.1 – Цифровая система управления На рисунке 6.1 t – непрерывное время, tк– дискретные моменты времени –моменты квантования. Сигнал y(tк) интерпретируется как числовая последовательность. Программа ЭВМ обрабатывает последовательность y(tк) и вычисляет новую последовательность u(tк). ЦАП преобразует последовательность u(tк) в непрерывный сигнал u(t). Интервал времени между моментами квантования называется периодом квантования h. Основная особенность цифровой системы управления в том, что она разомкнута между моментами квантования tk. Под квантованием, или дискретизацией, или выборкой понимают замену непрерывного по времени сигнала последовательностью чисел, представляющих значения сигнала в определенные моменты времени. Обратный процесс преобразования последовательности чисел в непрерывный сигнал называется восстановлением сигнала. Основная проблема квантования непрерывных сигналов – определение частоты квантования fs 1/h, при которой непрерывный сигнал однозначно может быть представлен последовательностью чисел, или дискрет. 6.1.2 Дискретизация непрерывных систем конечными разностямиПередаточная функция определяет некоторое дифференциальное уравнение, для дискретизации которого проще всего воспользоваться аппроксимацией первых производных конечными разностями по методу Эйлера. Прямая разностьмежду новым и предыдущим значениями: 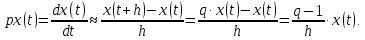 Обратная разность между текущим и предыдущим значениями: 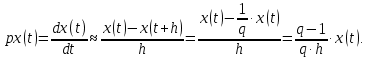 Аппроксимация, аналогичная методу трапеций в численном интегрировании задаётся уравнением: 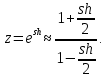 В цифровом управлении это приближение часто называют аппроксимацией Тустена (Тастина) или билинейным преобразованием. Использование этих методов аппроксимации приводит к тому, что импульсная передаточная функция 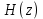 получается из непрерывной функции получается из непрерывной функции 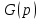 простой заменой аргумента простой заменой аргумента 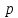 на на 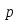 , где для метода Эйлера: , где для метода Эйлера: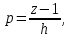 для аппроксимации обратной разностью: 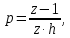 для аппроксимации Тастина: 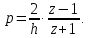 После аппроксимации Тастина дискретная система остается устойчивой, тогда как метод Эйлера этого гарантировать не может. 6.1.3 Составление моделей цифровых фильтровИсходными данными для разработки моделей цифровых регуляторов и фильтров являются передаточные функции, как правило, типовых алгоритмических звеньев, представленные в операторной непрерывной форме. В моём случае исходной является функция апериодического звена первого порядка: 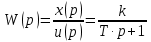 Для составления моделей цифровых фильтров на основе разностных уравнений, являющихся дискретными аналогами непрерывных передаточных функций, использую способы перехода от передаточных функций к разностным уравнениям, представленные ниже. При замене первой производной обратной разностью Передаточная функция: 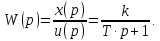 Заменяю первую производную обратной разностью: 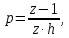 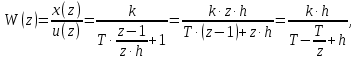 далее решаю последнее уравнение относительно 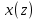 : :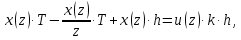 получаю: 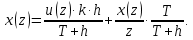 При замене первой производной формулой билинейного преобразования (аппроксимацией Тастина) Передаточная функция: 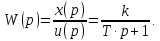 Заменяю первую производную формулой билинейного преобразования: 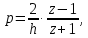 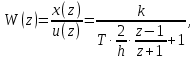 далее решаю последнее уравнение относительно 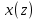 : :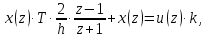 умножу обе части уравнения на 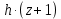 : :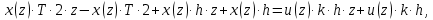 теперь разделю обе части на 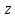 : :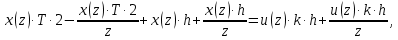 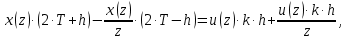 получаю: 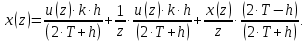 6.1.4 Моделирование цифровых фильтровПостроенные модели цифрового фильтра первого порядка, представленные в программе Matlab, среде Simulink: - модель непрерывной передаточной функции интегратора в форме аппроксимации обратной разностью и аппроксимации Тастина представлена на рисунке 6.2; - модель дискретного представления передаточной функции интегратора в форме аппроксимации обратной разностью представлена на рисунке 6.3; - модель дискретного представления передаточной функции интеграции в форме аппроксимации Тастина представлена на рисунке 6.4. Для построения графиков и их сравнения принимаю: постоянную времени фильтра равной постоянной интегральной части ПИ-регулятора скорости в системе векторного управления ( 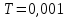 сек); коэффициент передачи фильтра равным коэффициенту передачи регулятора скорости ( сек); коэффициент передачи фильтра равным коэффициенту передачи регулятора скорости (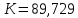 ); период квантования равным 0,1∙ ); период квантования равным 0,1∙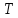 (то есть (то есть 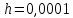 сек). сек).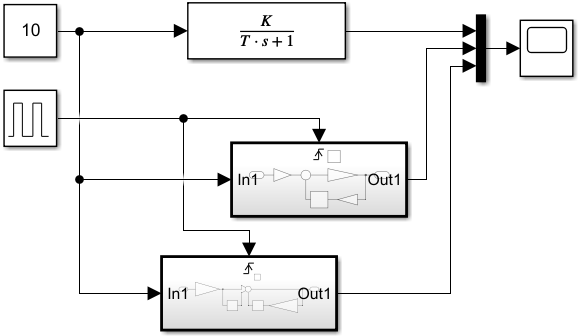 Рисунок 6.2 – Модель непрерывной передаточной функции апериодического звена первого порядка в форме аппроксимации обратной связью и апроксимации Тастина 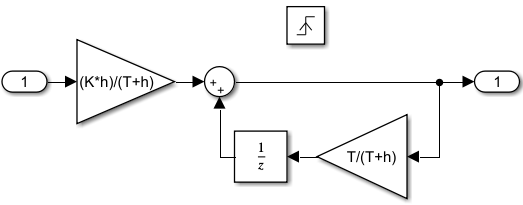 Рисунок 6.3 – Модель дискретного представления передаточной функции апериодического звена первого порядка в форме аппроксимации обратной разностью 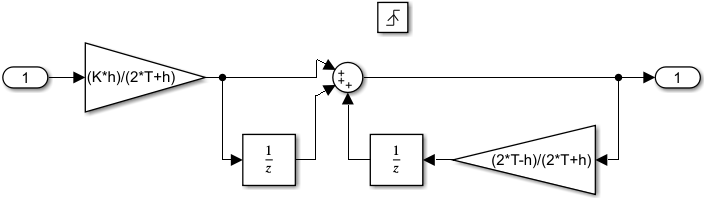 Рисунок 6.4 – Модель дискретного представления передаточной функции апериодического звена первого порядка в форме аппроксимации Тастина Графики, полученные при помощи вышеописанных моделей представлены на рисунке 6.5. На графиках (рисунок 6.5) можно наблюдать то, что я получил по формулам: период квантования 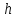 для аппроксимации Тастина становится меньше в два раза, по сравнению с аппроксимацией обратной разностью. для аппроксимации Тастина становится меньше в два раза, по сравнению с аппроксимацией обратной разностью. 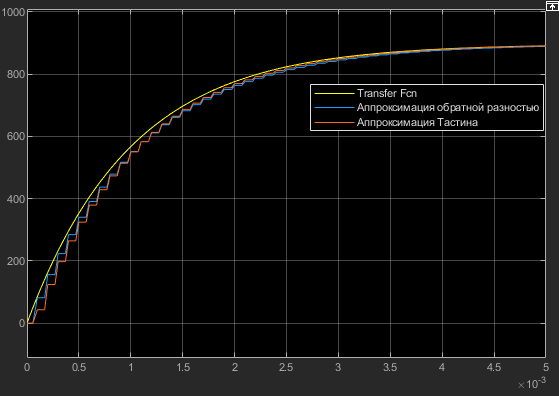 Рисунок 6.5 – Графики, полученные при аппроксимации непрерывной передаточной функции апериодического звена первого порядка: обратной разностью и аппроксимацией Тастина 6.2 Программная реализация цифрового фильтра первого порядкаДля программной реализации цифровых регуляторов и фильтров используют различные языки программирования, наиболее распространёнными из которых являются языки высокого уровня для ЭВМ (С, Паскаль) и программируемых логических контроллеров (ПЛК) (язык С, язык структурирования текста STL), и специализированные языки, в том числе для ЭВМ язык ассемблер, для ПЛК язык инструкций (IL). Программа на языке высокого уровня представляет собой набор операторов; на языках ассемблер или инструкций последовательность мнемонических обозначений машинных команд процессора. Исходными данными для разработки программы реализации цифровых регуляторов и фильтров являются передаточные функции, как правило, типовых алгоритмических звеньев, представленные в операторной непрерывной форме. Программы составляют на основе разностных уравнений, являющихся дискретными аналогами непрерывных передаточных функций. Передаточные функции, которые являются исходными данными для разработки программы реализации цифрового фильтра первого порядка, получены в предыдущем подразделе, в моём случае для апериодического звена первого порядка: - при аппроксимации обратной разностью: 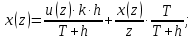 - при аппроксимации Тастина: 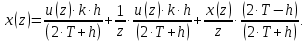 Программная реализация цифрового фильтра так же будет осуществляться при помощи ПО Matlab в среде Simulink. Составленная модель для реализации программ представлена на рисунке 6.6. В блоках Triggered Subsystem (которым на вход поступают значения 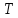 ; ; 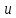 ; ; 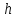 ; коэффициента ; коэффициента 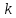 (в модели обозначен (в модели обозначен 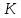 )) собраны модели, представленные на рисунке 6.7. )) собраны модели, представленные на рисунке 6.7.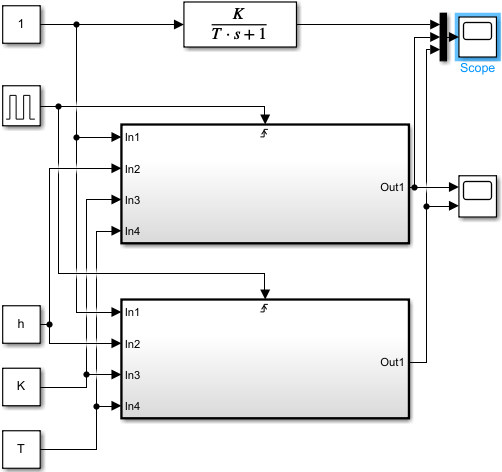 Рисунок 6.6 – Модель для программной реализации фильтра первого порядка 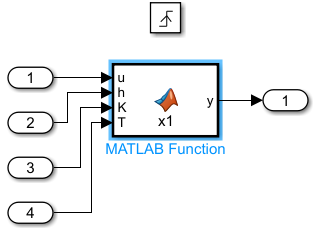 Рисунок 6.7 – Модели в блоках Triggered Subsystem В блоках MATLAB Function (рисунок 6.7) записан текст программ для реализации представления передаточной функции интегратора в форме: аппроксимации обратной разностью (программа представлена на рисунке 6.8); аппроксимации Тастина (программа представлена на рисунке 6.9).  Рисунок 6.8 – Программа реализации представления передаточной функции апериодического звена первого порядка в форме аппроксимации обратной разностью 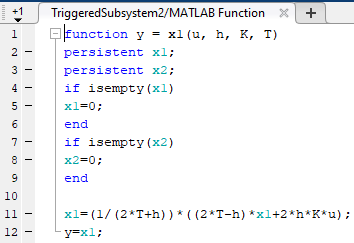 Рисунок 6.9 – Программа реализации представления передаточной функции апериодического звена первого порядка в форме аппроксимации Тастина По составленным программам произвожу моделирование и получаю графики, которые представлены на рисунке 6.10 (моделирование происходит при тех же условиях, что и в подразделе 6.1: постоянная времени фильтра равна постоянной интегральной части ПИ-регулятора скорости в системе векторного управления ( 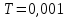 сек); коэффициент передачи фильтра равен коэффициенту передачи регулятора скорости ( сек); коэффициент передачи фильтра равен коэффициенту передачи регулятора скорости (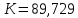 ); период квантования равен 0,1∙ ); период квантования равен 0,1∙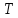 (то есть (то есть 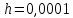 сек)). сек)).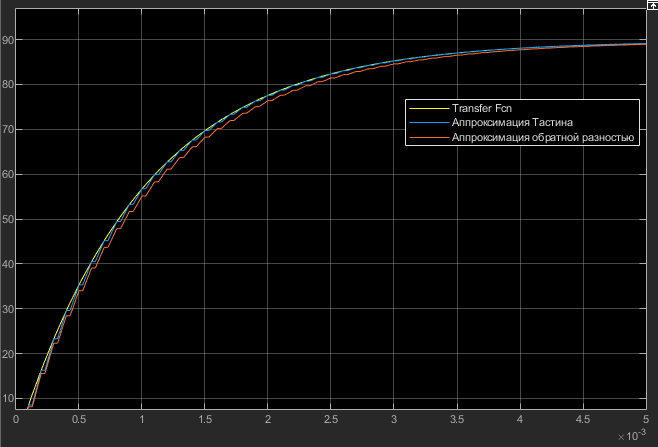 Рисунок 6.10 – Результаты программной реализации дискретного представления передаточной функции интегратора в форме аппроксимации обратной разностью и аппроксимации Тастина Заключение по разделу Сравнивая графики, полученные в обоих подразделах раздела 6, можно сделать вывод, что модель дискретного представления передаточной функции интегратора в форме апроксимации Тастина точнее модели дискретного представления передаточной функции интегратора в форме апроксимации обратной связью. ЗаключениеПри выполнении курсовой работы я приобрел практические навыки, необходимые для получения данных для расчёта параметров схемы замещения асинхронного электродвигателя, для синтеза и моделирования системы векторного управления электроприводом, для синтеза и моделирования системы скалярного управления электроприводом, как расчётным путём, так и при помощи программирования в среде Matlab. Также научился реализовывать системы управления в среде Simulink Matlab и могу сделать вывод о том, что скалярное управление электродвигателем точнее, чем векторное, оно позволяет получить менее колебательные переходные процессы, но недостаток подобного принципа управления заключается в трудности реализации желаемых законов регулирования скорости и момента АД в динамических режимах. Связано это весьма сложными электромагнитными процессами, протекающими в асинхронных двигателях [1]. Изучив и выбрав преобразователь частоты, на практике убедился в том, что использование преобразователя частоты приведёт к хорошей защите и оптимальным режимам работы электродвигателя, а также продлит срок его службы. Также я освоил во время выполнения курсовой работы метод представления электродвигателя в качестве конечного автомата, научившись при этом работать на языке лестничных диаграмм, освоил методы синтеза цифрового фильтра нижних частот. Список литературы1. Терехов В. М., Осипов О. И. Системы управления электроприводов [Текст]: учебник, под редакцией В. М. Терехова. – М.: Академия, 2005. – 300 с. 2. Кравчик А. Э., Шлаф М. М., Афонин В. И., Соболенская Е. А. Асинхронные двигатели серии 4А [Текст]: Справочник. Москва, Энергоиздат, 1982. – 504 с. 3. Теория автоматического управления [Текст]: учебное пособие для вузов / сост.: В. А. Лукас; М.: Недра, 1990. – 416 с. 4. Преобразователи частоты VLT AutomationDrive FC302 [Электронный ресурс] // Сайт компании Danfoss A/S. URL: https://www.danfoss.com/ru-ru/products/ac-drives/dds/vlt-automationdrive-fc-301-fc-302/#tab-overview (дата обращения: 23.12.2020). 5. Острем К. Виттенмарк Б. Системы управления с ЭВМ. – М.: Мир, 1987. – 300 с. Приложение АТехнические характеристики ПЧ при питании от сети 380 В. 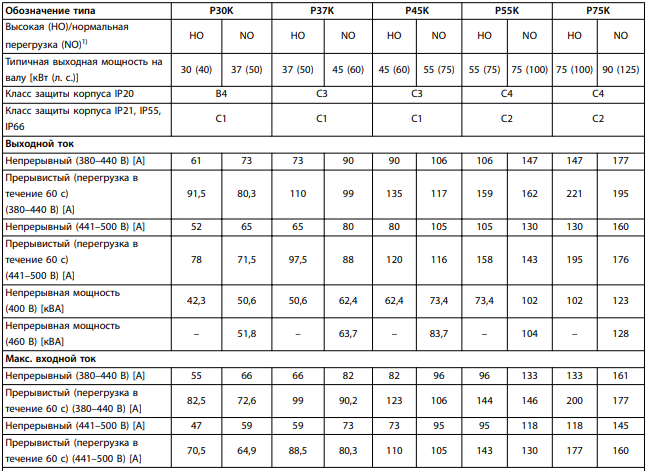 |
