Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
 Скачать 0.72 Mb.
|
Лабораторная работа №6.«Метод прогонки для трехдиагональных систем»Цель: научиться вычислять корни систем линейных алгебраических уравнений различными методами. Задание:Решить систему линейных алгебраических уравнений с помощью метода прогонки. И определить невязку и сделать анализ точности вычислений. Варианты заданий:
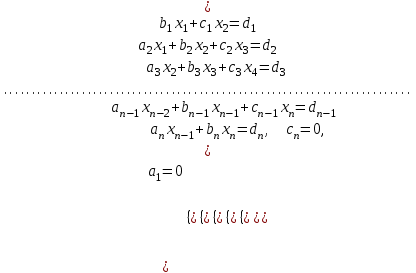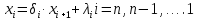Теоретический материал: Метод прогонки является одним из эффективных методов решения СЛАУ с трех - диагональными матрицами, возникающих при конечно-разностной аппроксимации задач для обыкновенных дифференциальных уравнений (ОДУ) и уравнений в частных производных второго порядка и является частным случаем метода Гаусса. Рассмотрим следующую СЛАУ:  решение, которое будем искать в виде: Где 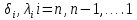 - прогоночные коэффициенты, подлежащие определению.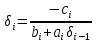 ,  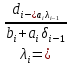;Пример решения СЛАУ методом прогонки в MatLab : 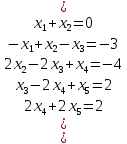 Решение: Найти коэффициенты прогонки 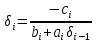,  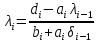Прямая прогонка A=[1,1,0,0,0;-1,1,-1,0,0;0,2,-2,1,0;0,0,1,-2,1;0,0,0,2,2] A = 1 1 0 0 0 -1 1 -1 0 0 0 2 -2 1 0 0 0 1 -2 1 0 0 0 2 2 >> B=[0;-3;-4;2;2] B = 0 -3 -4 2 2 >> %обозначим коэффициенты прогонки δ=d, λ=n >> d1=-A(1,2)/A(1,1) d1 = -1 >> n1=B(1,1)/A(1,1) n1 = 0 >>d2=-A(2,3)/(A(2,2)+A(2,1)*d1) d2 = 0.5000 >> n2=(B(2,1)-A(2,1)*n1)/(A(2,2)+A(2,1)*d1) n2 = -1.5000 >> d3=-A(3,4)/(A(3,3)+A(3,2)*d2) d3 = 1 >> n3=(B(3,1)-A(3,2)*n2)/(A(3,3)+A(3,2)*d2) n3 = 1 >> d4=-A(4,5)/(A(4,4)+A(4,3)*d3) d4 = 1 >> n4=(B(4,1)-A(4,3)*n3)/(A(4,4)+A(4,3)*d3) n4 = -1 >> n5=(B(5,1)-A(5,4)*n4)/(A(5,5)+A(5,4)*d4) n5 = 1 Получаем обратную прогонку Х5= λ5= n5=1 Х4=δ4*Х5+ λ4= d4*Х5+ n4= 0 Х3=δ3*Х4+ λ3= d3*Х4+ n3= 1 Х2=δ2*Х3+ λ2= d2*Х3+ n2=-1 Х1=δ1*Х2+ λ1= d1*Х2+ n1=1 Определим невязку >> A=[1,1,0,0,0;-1,1,-1,0,0;0,2,-2,1,0;0,0,1,-2,1;0,0,0,2,2] >> B=[0;-3;-4;2;2] >> X=[1;-1;1;0;1] >> R=B-A*X R = 0 0 0 0 0 Невязка равна нулю (т.к округлений вовремя вычислений не было) => найдено точное решение. Содержание отчета: 1. Титульный лист. 2. Цель лабораторной работы. 3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. 4. Расчетная часть: описание выполнения задания. 5. Выводы и анализ полученных результатов. Контрольные вопросы: Суть метода прогонки. В каких случаях возможно решение систем уравнений методом прогонки? С помощью, какой функции в MatLab можно вычислить определитель матрицы? С помощью, какой функции в MatLab можно ввести матрицу? Что значит решить СЛАУ? Какие матрицы называются трехдиагональными? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||