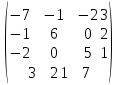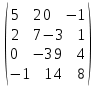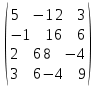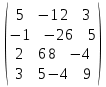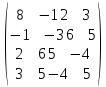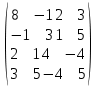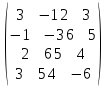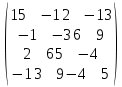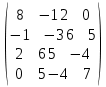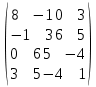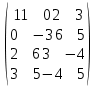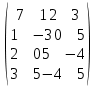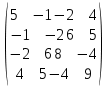Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
Лабораторная работа №9.«Численное решение алгебраических проблем собственных значений»Цель: Изучить методы нахождения собственных значений матрицы. Задание: Найдите наибольшее по модулю собственное число и соответствующий ему собственный вектор. Степенным методом Методом скалярных произведений (В качестве начального взять вектор [1,1,1,1] или [1,0,0,0]) Решить полную проблему собственных значений методом вращения Якоби; Используя среду MatLab проверить вычисления; Варианты заданий:
Теоретический материал:Рассмотрим матрицу  в n - мерном вещественном пространстве в n - мерном вещественном пространстве  векторов векторов . .1. Собственным вектором  матрицы A называется ненулевой вектор, удовлетворяющий равенству матрицы A называется ненулевой вектор, удовлетворяющий равенству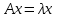 , , где 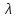 - собственное значение матрицы A, соответствующее рассматриваемому собственному вектору. - собственное значение матрицы A, соответствующее рассматриваемому собственному вектору.2. Собственные значения матрицы A с действительными элементами могут быть вещественными различными, вещественными кратными, комплексными попарно сопряженными, комплексными кратными. Степенной метод:РМ-алгоритм. Шаг 1. Ввести 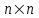 -матрицу А, задать -матрицу А, задать 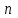 -мерный вектор -мерный вектор 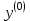 , вычислить , вычислить 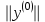 и вектор и вектор 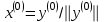 ; положить ; положить 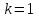 . .Шаг 2. Вычислить вектор 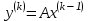 . .Шаг 3. Вычислить  и и 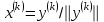 . .Шаг 4.Вычислить отношения 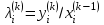 (координат векторов (координат векторов  и и 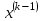 ) при ) при  таких, что таких, что  , где , где 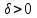 - некоторое задаваемое малое число (допуск). - некоторое задаваемое малое число (допуск).Шаг 5. Подвергнуть числа 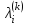 тесту на сходимость. тесту на сходимость. Если обнаруживается совпадение требуемого числа знаков в 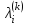 и и 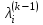 ( ( можно задавать произвольно), то работу алгоритма прекратить и за старшее собственное число можно задавать произвольно), то работу алгоритма прекратить и за старшее собственное число  принять усредненное (по принять усредненное (по 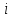 ) значение ) значение 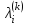 , а за нормированный старший собственный вектор , а за нормированный старший собственный вектор 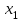 -вектор -вектор 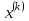 . .В противном случае – вернуться к шагу 2. Метод скалярных произведений:SP-алгоритм. Ввести: данную симметричную 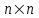 -матрицу А, произвольный -матрицу А, произвольный 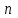 -мерный начальный вектор -мерный начальный вектор 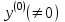 , малое число , малое число 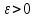 (определяющее допустимую абсолютную погрешность искомого собственного числа (определяющее допустимую абсолютную погрешность искомого собственного числа  ), число ), число  для начального сравнения (например, 0). Положить для начального сравнения (например, 0). Положить 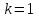 (счетчик итераций). (счетчик итераций).Вычислить скаляры 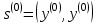 , , 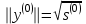 и вектор и вектор 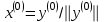 . .Вычислить 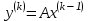 (итерация нормированного вектора). (итерация нормированного вектора).Вычислить: 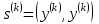 и и 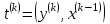 (скалярные произведения), (скалярные произведения), 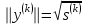 , , 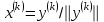 (приближение к нормированному собственному вектору), (приближение к нормированному собственному вектору), 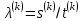 (приближение к собственному числу (приближение к собственному числу  ). ).Если 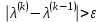 , положить , положить  и вернуться к шагу 3, иначе завершить работу алгоритма, считая и вернуться к шагу 3, иначе завершить работу алгоритма, считая 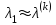 , , 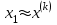 . .Метод вращений ЯкобиМетод вращений Якоби применим только для симметрических матриц 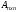 ( (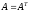 ) и решает полную проблему собственных значений и собственных векторов таких матриц. Он основан на отыскании с помощью итерационных процедур матрицы ) и решает полную проблему собственных значений и собственных векторов таких матриц. Он основан на отыскании с помощью итерационных процедур матрицы 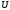 в преобразовании подобия в преобразовании подобия  , а поскольку для симметрических матриц , а поскольку для симметрических матриц 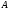 матрица преобразования подобия матрица преобразования подобия 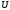 является ортогональной ( является ортогональной (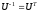 ), то ), то  , где , где  - диагональная матрица с собственными значениями на главной диагонали - диагональная матрица с собственными значениями на главной диагонали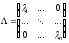 . .Пусть дана симметрическая матрица A. Требуется для нее вычислить с точностью 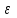 все собственные значения и соответствующие им собственные векторы. Алгоритм метода вращения следующий: все собственные значения и соответствующие им собственные векторы. Алгоритм метода вращения следующий:Пусть известна матрица 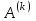 на k–й итерации, при этом для k=0 на k–й итерации, при этом для k=0 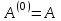 . .1. Выбирается максимальный по модулю недиагональный элемент 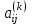 матрицы матрицы 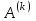 ( ( 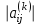 = = ) . ) .2. Ставится задача найти такую ортогональную матрицу 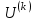 , чтобы в результате преобразования подобия , чтобы в результате преобразования подобия 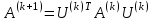 произошло обнуление элемента произошло обнуление элемента 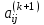 матрицы матрицы 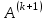 . В качестве ортогональной матрицы выбирается матрица вращения, имеющая следующий вид: . В качестве ортогональной матрицы выбирается матрица вращения, имеющая следующий вид: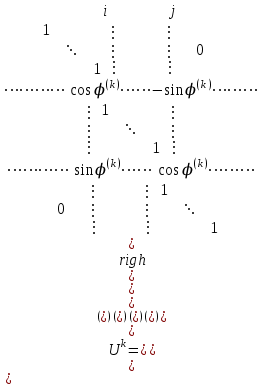 , , В матрице вращения на пересечении 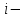 й строки и й строки и 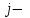 го столбца находится элемент го столбца находится элемент 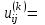 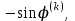 где где 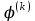 - угол вращения, подлежащий определению. Симметрично относительно главной диагонали ( - угол вращения, подлежащий определению. Симметрично относительно главной диагонали ( -я строка, -я строка, 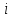 -й столбец) расположен элемент -й столбец) расположен элемент 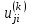 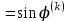 ; Диагональные элементы ; Диагональные элементы 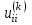 и и 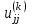 равны соответственно равны соответственно 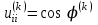 , , 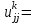  ; другие диагональные элементы ; другие диагональные элементы 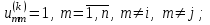 остальные элементы в матрице вращения остальные элементы в матрице вращения 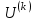 равны нулю. равны нулю. Угол вращения 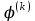 определяется из условия определяется из условия 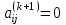 : :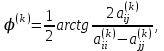 причем если причем если 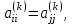 то то 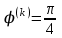 . .3. Строится матрица 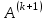 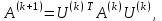 в которой элемент 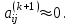 В качестве критерия окончания итерационного процесса используется условие малости суммы квадратов внедиагональных элементов: 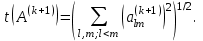 Если 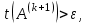 то итерационный процесс то итерационный процесс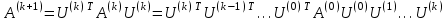 продолжается. Если  , то итерационный процесс останавливается, и в качестве искомых собственных значений принимаются , то итерационный процесс останавливается, и в качестве искомых собственных значений принимаются 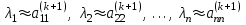 . .Координатными столбцами собственных векторов матрицы 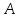 в единичном базисе будут столбцы матрицы в единичном базисе будут столбцы матрицы 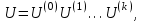 т.е. т.е. 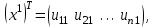  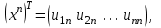 причем эти собственные векторы будут ортогональны между собой, т.е. 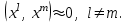 Пример решение проблемы собственных значений в среде MatLab:Поиск ненулевых решений системы АХ=λX в среде MatLab реализуется командами d=eig(A) или [X,d]=eig(A), где d - диагональная матрица собственных чисел, Х –матрица из нормированных собственных векторов. Например, задав матрицу
командой [R,D]=eig(А) получаем:
Возьмем другую матрицу
с известными собственными значениями –3, 1, 1. Выполнив ту же команду [R,D]=eig(А), получаем:
Обратите внимание на эффект погрешности (мнимая часть у ряда компонент собственных векторов весьма велика). Поэтому при значительных размерностях и особых случаях (кратные и близкие собственные значения) проверка качества поиска весьма желательна (достаточно проверить на близость к нулю значений A*R-R*D). Содержание отчета: Титульный лист. Цель лабораторной работы. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. Расчетная часть: описание выполнения задания Проверка результатов в среде MatLab. Выводы и анализ полученных результатов. Контрольные вопросы: Что такое собственное число матрицы и как оно вычисляется? Что такое собственный вектор и как он находится? В чем суть степенного метода; Алгоритм вычисления собственного значения и собственного вектора матрицы методом скалярных произведений; Метод вращений Якоби численного решения задач на собственные значения и собственные векторы матриц Какими командами реализуется поиск ненулевых решений системы АХ=λX в среде MatLab; |