Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11

• Название: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
• Дата: 27.04.2023
• Размер: 0.72 Mb.
• Имя файла: Мет.указания по лабораторным работам.docx
• Тип: Лабораторная работа; #1093112
• страница: 10 из 14

Интерполяционная схема Эйткена

Применение формулы Лагранжа для вычисления интерполяционного многочлена в точке неудобно из-за ее громоздкости. Существенно упростить расчет интерполяционного многочлена в конкретной точке можно, используя интерполяционную схему Эйткена, которая заключается в следующем.

На первом этапе строится последовательность многочленов первой степени по двум рядом стоящим узлам: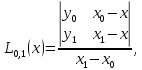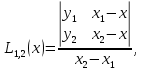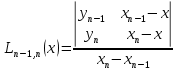









Очевидно, что все построенные многочлены являются многочленами Лагранжа (здесь 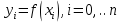  ) На втором этапе строится последовательность многочленов Лагранжа 2-й степени, при этом используются многочлены, вычисленные на предыдущем этапе. Расчеты выполняются по формулам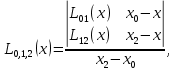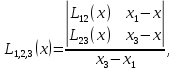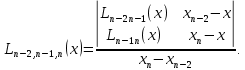







Количество таких многочленов будет на 1 меньше, чем на предыдущем этапе. Наконец на n-м этапе строится многочлен Лагранжа степени n по формуле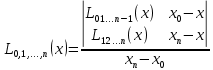

Это и будет значение многочлена Лагранжа степени n  в точке   x , построенного по узлам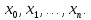  

Пример построения интерполяционного многочлена Лагранжа в среде MatLab7.0 по таблице:

x	-1	0	1	2	X
y	4	2	0	1	1.5

1.Введем данные:

>> x = [-1 0 1 2]

>> y = [4 2 0 1]

2.Построим интерполяционный многочлен (аппроксимация третьей степени):

>> p = polyfit(x, y, 3)

Коэффициенты интерполяции

p = 0.5000 0.0000 -2.5000 2.0000

Многочлен Лагранжа

L=0.5*x.^3-2.5*x+2

3.Построим график функции и узлы интерполяции (см. Рисунок 4). Для графика зададим больше значений, чем в исходной таблице

>> x1=[-1:0.1:2];

>> L=0.5*x1.^3-2.5*x1+2 ;

>> plot(x1, L, 'r', x, y, '*')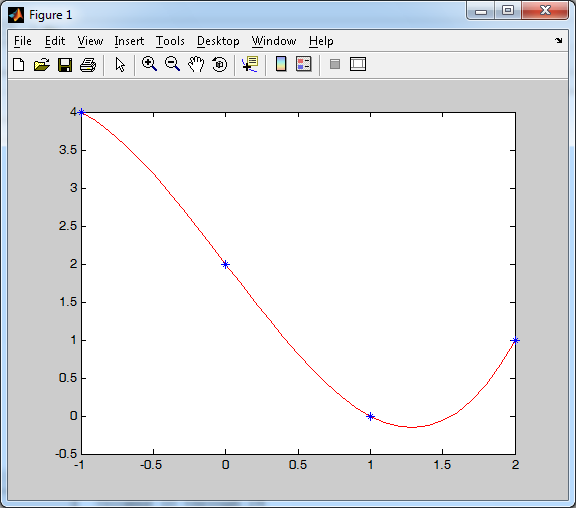


Рисунок 4. График функции
Содержание отчета:

1. 
   Титульный лист.
   
2. 
   Цель лабораторной работы.
   
3. 
   Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.
   
4. 
   Расчетная часть: описание выполнения задания
   
5. 
   Проверка результатов в среде MatLab.
   
6. 
   Выводы и анализ полученных результатов.
   

Контрольные вопросы:

1. 
   Постановка задачи теории интерполирования;
   
2. 
   Интерполяционный многочлен Лагранжа;
   
3. 
   Остаточный член интерполяционной формулы Лагранжа и его оценка;
   
4. 
   Вычислительная схема Эйткена;
   
5. 
   Какими командами реализуется построение графиков в среде MatLab;
   
6. 
   Что означает запись: 0.5*x.^3 в среде MatLab;
   

Лабораторная работа №11.

« Интерполирование. Интерполяционные формулы»

Цель: научиться применять интерполяционные формулы для заданной совокупности данных.
Задание:

1.      Подобрать интерполяционный полином по формулам Ньютона для следующей совокупности данных x_i, y_i., найти значение полинома в точках z1 и z2, найти погрешность.

2.      Вычислить значения функции в точках z3 и z4, используя сплайн-интерполяцию.

3.      Найти значения функции в точках z1, z2, z3, z4 используя среду MatLab.

Варианты заданий:

Вариант	xi	1	2	3	4	5	z1	z2	z3	z4
	yi	0,7	1,9	1,1	2,2	3,5	2,2	4,8	2,1	1,1
	yi	0,8	2,4	1,5	2,3	4,0	1,2	4,6	4,6	1,1
	yi	2,1	3,0	1,5	3,2	4,1	1,8	4,4	1,1	3,3
	yi	2,2	4,8	1,9	3,9	5,5	2,2	4,9	3,5	2,5
	yi	1,0	3,5	5,0	5,6	3,8	1,1	4,8	2,1	4,8
	yi	2,6	1,1	1,6	3,2	2,4	1,5	3,9	4,5	3,9
	yi	3,5	4,8	3,5	1,8	1,5	2,1	4,2	1,3	2,1
	yi	6,0	3,2	1,9	1,3	1,2	1,9	4,1	4,9	1,9
	yi	1,5	1,8	2,5	4,0	7,0	2,2	4,8	4,8	3,6
	yi	0	6,0	2,0	1,3	6,0	1,2	4,9	1,2	2,2
	yi	3,5	1,2	0	1,7	2,0	1,1	3,8	3,8	4,7
	yi	1,4	2,7	6,0	0	4,8	1,9	4,9	1,9	2,3
	yi	2,1	3,1	5,1	5,8	6,0	2,1	4,8	2,1	3,3
	yi	1,3	2,4	6,0	0	4,6	1,1	4,7	1,1	2,9
	yi	1,0	3,5	5,0	5,6	3,8	1,1	4,8	2,1	4,8

Теоретический материал:
Вычисление значений функции для значений аргумента, лежащих в начале таблицы, удобно проводить, пользуясь первой интерполяционной формулой Ньютона.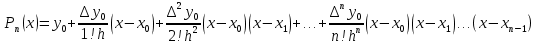



Для интерполирования в конце таблицы обычно применяют вторую интерполяционную формулу Ньютона.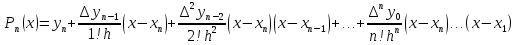



Примеры решения задач интерполяции в MatLab:
1. Интерполяция кубическими сплайнами в среде Matlab осуществляется с помощью функции spline, которая имеет вид:

Y_i = spline(x, у, xi).

Здесь:

• 
  x — вектор узлов интерполяции;
  
• 
  у — вектор значений функции в узлах интерполяции;
  
• 
  xi — вектор аргументов функции y(x) из области ее определения, зада­ваемый пользователем.
  

Вместо вектора у функция у =f(x) может быть задана в виде формулы.

Функция spline не позволяет получить функцию интерполяции в виде фор­мулы. В этом ее существенный недостаток.

Пусть в результате опыта получены данные:

	Значение переменных
x	1	4	7	9	13	18	21	27
y	0.4	1.55	2.9	3.9	5.86	8.3	9.8	12.8

Необходимо найти значения функции при x = 3, 6, 10, 14, 20. Процедуры интерполяции будут иметь вид:

x= [1 4 7 9 13 18 21 27];

у= [0.4, 1.55, 2.9, 3.9, 5.86, 8.3, 9.8, 12.8];

xi =[3 6 10 14 20];

Yi = spline(х, у, xi)

После нажатия клавиши <Enter> на экране увидим ответ:

Yi= 1.1458 2.4261 4.3980 6.3444 9.2975
2.Функция interpl наиболее универсальна, она позволяет решать задачи интерполяции несколькими методами.

Функция имеет вид:

Y_i = interpl (х, у, xi ,метод).

Здесь:

• 
  х, у, — векторы узлов и значений функции интерполяции;
  
• 
  xi — вектор значений аргументов, задаваемый пользователем;
  
• 
  метод— аргумент, позволяющий пользователю выбрать метод интерполяции.
  

Методами интерполяции в Matlab являются:

• 
  ‘nearest’— ступенчатая;
  
• 
  ‘linear’ — линейная;
  
• 
  ‘cubic’— кубическая;
  
• 
  ‘spline’ — кубическими сплайнами.
  

Если метод не указан, то реализуется линейная интерполяция.

Пусть функция у = f(х) задана в виде таблицы значений

	Значения переменных
x	2	3	8	12	20	25	36
y	1	2.5	4.6	6.8	5.1	3.9	3

Необходимо определить значения функции при значениях аргументов x= 4, 6, 15, 30.

x=[2, 3, 8, 12, 20, 25, 36];

у = [1, 2.5, 4.6, 6.8, 5.1, 3.9, 3] ;

xi = (4, 6, 15, 30);

yi = interpl (х, у, хi) —линейная интерполяция

yi = interpl (х, у, xi, ‘linear’) — линейная интерполяция

yi = interpl (х, у, xi, ‘nearest’) —ступенчатая интерполяции

yi = interpl (х, у, xi, ‘cubic’ ) —кубическая интерполяция

yi = inrerpi (х, у, xi, ‘spline’ ) — интерполяции кубическими сплай­нами.

В результате решения задачи получим следующие ответы:

• 
  линейная интерполяция: 2.92 3.76 6.1625 3.4909;
  
• 
  ступенчатая интерполяция: 2.5 4.6 6.8 3.9;
  
• 
  кубическая и кубическая сплайнами: 3.4133 4.16 6.9772 3.5263.
  

Из результатов решения видно, что ответы зависят от метода интерполяции. Какой же из них предпочтительней? Ответ на этот вопрос можно дать лишь после анализа погрешностей интерполяции.
3.Система Matlab позволяет обоснованно выбрать степень полинома при по­линомиальной интерполяции путем вычисления табличных разностей. Для этой цели служит функция diff. Эта функция имеет вид:

diff (v,n).

Здесь:

• 
  v — вектор функции y(x);
  
• 
  п — порядок конечных разностей.
  

Полиномиальная аппроксимация имеет смысл лишь тогда, когда n-ая ко­нечная разность функции у(х) при постоянном шаге изменения аргумента x является постоянной. При этом значение п является степенью полинома. Если это условие не выполняется, то многочлен степени п либо не может быть функцией интерполяции, либо является основным источником по­грешностей.

Пусть данные эксперимента сведены в таблицу:

	Значения переменных
x	1	2	3	4	5	6	7	8	9	10
y	18	52.2	121.4	239.4	420	677	1024.2	1475.4	2044.4	2745

Необходимо решить задачу полиномиальной аппроксимации.

Вначале определим степень полинома, воспользовавшись функцией diff. Эти процедуры в системе Matlab будут иметь вид:

х = [12 3 4 5 6 7 8 9 10);

у = [18, 52.2, 121.4, 239.4, 420, 677, 1024.2, 1475.4, 2044.4, 2745];

diff(y, 1)

ans = 34.2 69.2 118 180.6 257 347.2 451.2 569 700.6

diff(у, 2)

ans =35 48.8 62.6 76.4 90.2 104 117.8 131.6

diff(y, 3)

ans = 13.8 13.8 13.8 13.8 13.8 13.8 13.8

Табличные разности третьего порядка одинаковы, поэтому интерполяцион­ный полином будет иметь вид:

φ(x) = ах³+ bx² + сх + d.

Определим теперь значения коэффициентов а, d, с, d воспользовавшись функцией polyfit.

Так как векторы аргумента х и функции у уже введены, то достаточно вве­сти функцию polyfit.

р = polyfit(х, у, 3)

р = 2.3 3.7 7 5

Подставляя полученные значения в функцию у(х), получим:

φ(x) = 2.3 х³+ 3.7 x² + 7х + 5.

Проверим правильность решения задачи, воспользовавшись функцией polyval:

f = polyval(p, х)

f = 18 52.2 121.4 239.4 420 677 1024.2 1475.4 2044.4 2745

Сравнивая значения fс исходными значениями у, видим, что они совпада­ют. Задача решена с нулевой погрешностью.
Содержание отчета:

1. 
   Титульный лист.
   
2. 
   Цель лабораторной работы.
   
3. 
   Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.
   
4. 
   Расчетная часть: описание выполнения задания
   
5. 
   Проверка результатов в среде MatLab.
   
6. 
   Выводы и анализ полученных результатов.
   

Контрольные вопросы:

1. 
   Интерполяционный многочлен Ньютона;
   
2. 
   В каких случаях ставится задача интерполирования функций?
   
3. 
   Какой формулой Вы пользовались для интерполирования?
   
4. 
   Какие узлы интерполирования даны в Вашем случае (равноотстоящие или произвольные)?
   
5. 
   Какие интерполяционные формулы используются при произвольных узлах?
   
6. 
   В чем заключается кусочная интерполяция?
   
7. 
   Какие функции используются для интерполирования функции в среде MatLab?
   
8. 
   Что находит функция p = polyfit(x, y, n);