Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
СодержаниеСодержание 1 Лабораторная работа №1. 3 «Основы теории погрешностей» 3 Лабораторная работа №2. 11 «Основы теории погрешностей» 11 Лабораторная работа №3-4. 19 «Решение нелинейных уравнений» 19 Лабораторная работа №5. 27 «Решение систем линейных алгебраических уравнений» 27 Лабораторная работа №6. 34 «Метод прогонки для трехдиагональных систем» 34 Лабораторная работа №7. 39 « Использование итерационных численных методов для решения СЛАУ» 39 Лабораторная работа №8. 47 « Использование итерационных численных методов для решения СЛАУ» 47 Лабораторная работа №9. 53 «Численное решение алгебраических проблем собственных значений» 53 Теоретический материал: 56 Степенной метод: 56 Метод скалярных произведений: 57 Метод вращений Якоби 58 Пример решение проблемы собственных значений в среде MatLab: 61 Лабораторная работа №10. 63 «Интерполирование. Интерполяционные формулы» 63 Интерполяционная схема Эйткена 64 Лабораторная работа №11. 68 « Интерполирование. Интерполяционные формулы» 68 Лабораторная работа №12. 75 «Аппроксимация, построение аппроксимирующих кривых» 75 Лабораторная работа 13. 82 «Численное дифференцирование функции. Методы дифференцирования» 82 Лабораторная работа №14. 88 « Численное интегрирование функции» 88 Лабораторная работа №15 95 «Численные методы решения дифференциальных уравнений» 95 Список использованной литературы 94 Лабораторная работа №1.«Основы теории погрешностей» 4 Лабораторная работа №2.«Основы теории погрешностей» 11 Лабораторная работа №3-4.«Решение нелинейных уравнений» 18 Лабораторная работа №5.«Решение систем линейных алгебраических уравнений» 25 Лабораторная работа №6.«Метод прогонки для трехдиагональных систем» 32 Лабораторная работа №7.« Использование итерационных численных методов для решения СЛАУ» 37 Лабораторная работа №8.« Использование итерационных численных методов для решения СЛАУ» 44 Лабораторная работа №9.«Численное решение алгебраических проблем собственных значений» 50 Лабораторная работа №10.«Интерполирование. Интерполяционные формулы» 59 Лабораторная работа №11.« Интерполирование. Интерполяционные формулы» 64 Лабораторная работа №12.«Аппроксимация, построение аппроксимирующих кривых» 70 Лабораторная работа 13.«Численное дифференцирование функции. Методы дифференцирования» 76 Лабораторная работа №14.« Численное интегрирование функции» 81 Лабораторная работа №15.«Численные методы решения дифференциальных уравнений» 88 Список использованной литературы 94 Лабораторная работа №1.«Основы теории погрешностей»Цель: Закрепление теоретического материала по теме значащие и верные цифры. Знакомство со средой MatLab 7.0. Задание №1. Округлить сомнительные числа, оставив верные знаки в узком смысле. Определить абсолютную погрешность результата. Варианты заданий: 9,86314  0,00074 0,0007427,45456;  0,4239 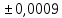 13,15466; 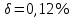 75,5242 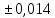 87,231; 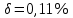 34,7856; 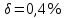 4,1236; 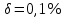 23,09870  0,0009 0,00093,41253  0,00023 0,0002333,60457; 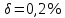 37,848  0,0079 0,00791,12486; 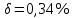 2,75387  0,00011 0,000115,75555;  Задание 2. Округлить сомнительные цифры числа, оставив верные знаки в широком смысле. Определить абсолютную погрешность результата. Варианты заданий: 29,7387  0,0013 0,001310,12486; 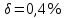 79,83014  0,00074 0,000745,75055;  23,0981  0,0003 0,00037,42503  0,00012 0,0001231,73856; 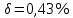 48,1026; 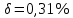 3,85508  0,00077 0,0007737,63457; 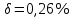 30,0039  0,0009 0,000912,35456; 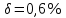 75,7242 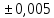 13,00466; 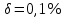 5,10459 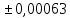 Задание №3.Определить, какое равенство точнее. Варианты заданий: 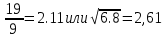 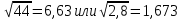 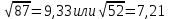 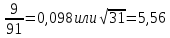 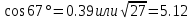 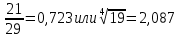 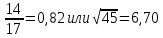  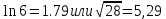 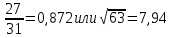 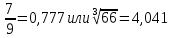 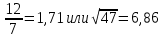 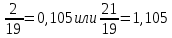 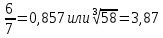 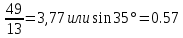 Теоретический материал: Значащей цифрой приближенного числа - называется всякая цифра в его десятичном изображении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда. Все остальные нули, входящие в состав приближенного числа и служащие лишь для обозначения десятичных разрядов его, не причисляются к значащим цифрам. Значащая цифра называется верной в широком смысле если абсолютная погрешность числа не превосходит одной единицы разряда, соответствующего этой цифре. Значащая цифра называется верной в узком смысле если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре. В противном случае цифра считается сомнительной. Краткие сведения, необходимые для работы в MATLAB: MATLAB - это популярная система компьютерной математики, которая предназначена для выполнения инженерных и научных вычислений. После запуска MATLAB на экране появляется основное окно приложения.(см. рисунок 1) Это окно содержит меню, панель инструментов и рабочую область - Command Window. Признаком готовности системы к выполнению команды является наличие знака приглашения », после которого расположен активный курсор. Рабочую область со знаком приглашения обычно называют командной строкой. Ввод команд в MATLAB осуществляется с клавиатуры. Нажатие клавиши Enter заставляет систему выполнить команду и вывести результат. Клавиши «Стрелка вверх» ↑ и «Стрелка вниз» ↓ управляют курсором, однако в MATLAB они имеют другое назначение. Эти клавиши позволяют вернуть в командную строку ранее введенные команды или другую входную информацию, так как вся эта информация сохраняется в специальной области памяти. Так, если в пустой активной командной строке нажать клавишу ↑, то появится последняя вводимая команда, повторное нажатие вызовет предпоследнюю и так далее. Клавиша ↓ выводит команды в обратном порядке. Зона редактирования - это фактически командная строка. В ней действуют элементарные приемы редактирования: → - перемещение курсора вправо на один символ; ← - перемещение курсора влево на одни символ; Ноmе - перемещение курсора в начало строки; End - перемещение курсора в конец строки; Del - удаление символа после курсора; Backspace - удаление символа перед курсором. К 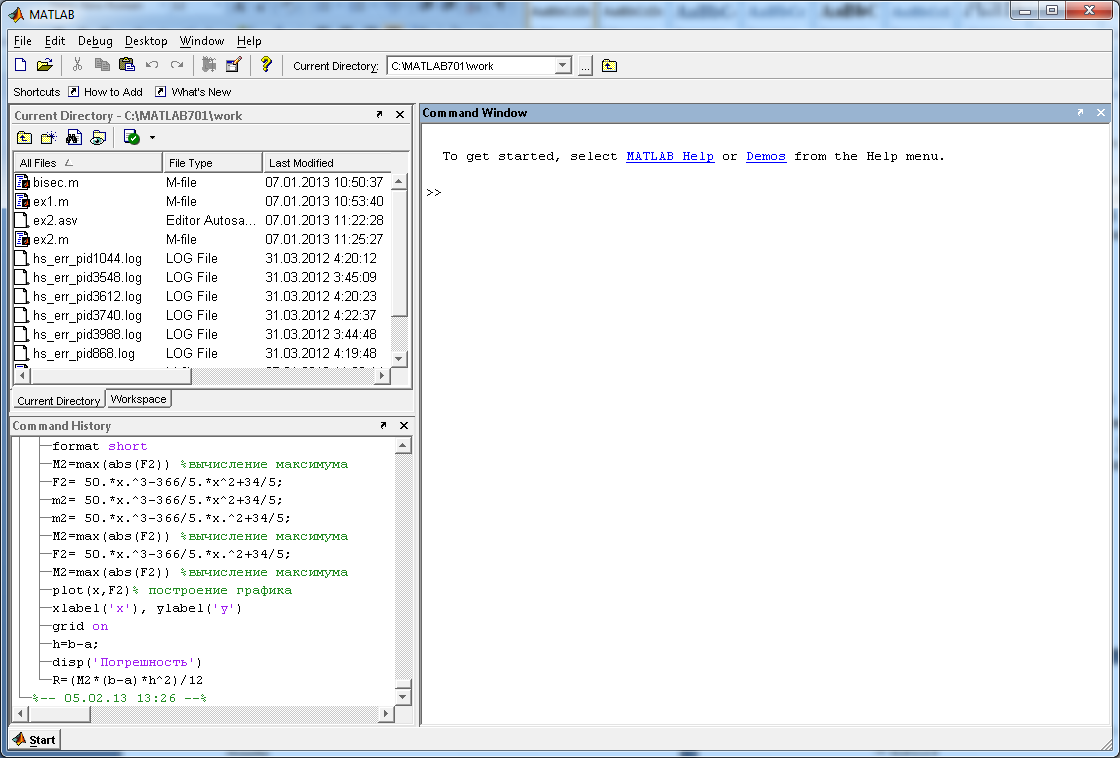 роме того, существуют особенности ввода команд. Если команда заканчивается точкой с запятой «;», то результат ее действия не отображается в командной строке. В противном случае, при отсутствии знака «;», результат действия команды сразу же выводится в рабочую область. роме того, существуют особенности ввода команд. Если команда заканчивается точкой с запятой «;», то результат ее действия не отображается в командной строке. В противном случае, при отсутствии знака «;», результат действия команды сразу же выводится в рабочую область.Рисунок 1. Основное окно приложения MatLab Пример №1. Задание: Определить, какое равенство точнее. 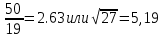 Решение: Сравним границы относительных погрешностей (предельно относительных погрешностей) 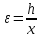 , определив границы абсолютных погрешностей , определив границы абсолютных погрешностей 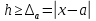 . Для этого вычислим значения исходных равенств с большим числом знаков после запятой: . Для этого вычислим значения исходных равенств с большим числом знаков после запятой: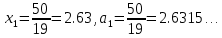 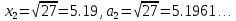 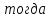 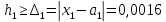 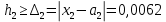 В свою очередь 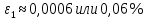 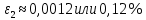 Так как 0,06% > 0,12%, то равенство 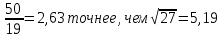 Вычисления в MatLab: >> a1=50/19 a1 = 2.6316 >> x1=2.63 x1 = 2.6300 >> a2=sqrt(27) a2 = 5.1962 >> x2=5.19 x2 = 5.1900 >> h1=abs(x1-a1) h1 = 0.0016 >> h2=abs(x2-a2) h2 = 0.0062 >> e1=h1/a1*100 e1 = 0.0600 >> e2=h2/a2*100 e2 = 0.1184 Пример №2. Задание: Округлить сомнительные числа, оставив верные знаки в узком смысле. Определить абсолютную погрешность результата. 1,784; 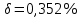 Решение: Используем определение: Цифра называется верной в узком смысле, если абсолютная погрешность не превосходит половины единицы десятичного разряда, выраженного этой цифрой. Найдем абсолютную погрешность исходного числа h=(0.352%*1.784)/100%=0.0063 (более точное вычисления не требуется, т.к. нас интересует, превосходит ли эта погрешность половину единицы десятичного разряда или нет). 0,0063 > 0,0005 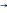 4 – сомнительная цифра в узком смысле. 4 – сомнительная цифра в узком смысле.0,0063 > 0,005 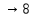 – сомнительная цифра в узком смысле. – сомнительная цифра в узком смысле.0,0063< 0,05 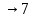 – верная цифра в узком смысле, занимает разряд десятичных долей, т.е. округляем до десятых: – верная цифра в узком смысле, занимает разряд десятичных долей, т.е. округляем до десятых:1,784 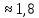 Проверим, все ли цифры получившегося числа являются верными. Для этого вычислим погрешность результата: 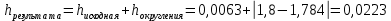 0,0223<0.05 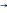 в числе 1,8 цифра 8 а, следовательно, и все предыдущие верны в узком смысле. Итак, ответ 1,8 в числе 1,8 цифра 8 а, следовательно, и все предыдущие верны в узком смысле. Итак, ответ 1,8 0,0223 0,0223Пример №3. Задание: Округлить сомнительные цифры числа, оставив верные знаки в широком смысле. Определить абсолютную погрешность результата. 0,85637; 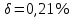 Решение: Используем определение: Цифра называется верной в широком смысле, если абсолютная погрешность этого числа не превосходит единицы десятичного разряда, выраженного этой цифрой. Вычислим абсолютную погрешность исходного числа: H=(0,85637*0,21%)/100%=0,0018 0,0018 > 0.00001 -7- сомнительная цифра в широком смысле; 0,0018 > 0.0001 -3- сомнительная цифра в широком смысле; 0,0018 > 0.001 -6- сомнительная цифра в широком смысле; 0,0018 < 0.01 -5- верная цифра в широком смысле; Таким образом, округлим исходное число до верных в широком смысле цифр: 0,85637 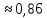 Проверим верность цифр округленного числа. Для этого вычислим погрешность результата 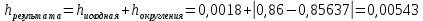 0,00543<0.01 – e у числа 0,86 все цифры верные в широком смысле. Содержание отчета: 1. Титульный лист. 2. Цель лабораторной работы. 3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. 4. Расчетная часть: описание выполнения задания в среде MatLab. 5. Выводы и анализ полученных результатов. Контрольные вопросы: Дайте определение приближенного числа Сформулируйте правила округления чисел. Как находится абсолютная погрешность приближенного числа. Как находится относительная погрешность приближенного числа. Верной цифрой в узком смысле называется ….. Верной цифрой в широком смысле называется ….. Как в среде MatLab записать элементарные математические функции: Синус числа Х Косинус числа Х Тангенс числа Х Котангенс числа Х Корень квадратный из числа Х Модуль числа Х Экспонента числа Х Натуральный логарифм числа Х |
