Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11

• Название: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
• Дата: 27.04.2023
• Размер: 0.72 Mb.
• Имя файла: Мет.указания по лабораторным работам.docx
• Тип: Лабораторная работа; #1093112
• страница: 14 из 14

Лабораторная работа №15

«Численные методы решения дифференциальных уравнений»

Цель работы. Освоить: методы решения дифференциальных уравнений с начальными условиями и метод прогонки решения краевой задачи для дифференциального уравнения второго порядка.
Задание1. Решить дифференциальное уравнение используя:

1. 
   Метод Эйлера
   
2. 
   Модифицированный метод Эйлера
   
3. 
   Метод Рунге-Кутта
   
4. 
   Среду Матлаб.
   

Варианты:

1. y' = x + y²; y(0) = 0,5.

2. y' = 2x + y²; y(0) = 0,3.

3. y' = 0,2x + y²; y(0) = 0,1.

4. y' = x² + 2y; y(0) = 0,1.

5. y' = x² + y²; y(0) = 0,7.

6. y' = 0,3x + y²; y(0) = 0,4.

7. y' = x + 0,3y²; y(0) = 0,3.

8. y' = 0,1x² + 2хy; y(0) = 0,8.

9. y' = 3x² + 0,1xy; y(0) = 0,2.

10. y' = x² + 0,1y²; y(0) = 0,7.

11. y' = 0,2x² + y²; y(0) = 0,8.

12. y' = 2x + 0,1y²; y(0) = 0,2.

13. y' = x² + xy; y(0) = 0,2.

14. y' = x² + y; y(0) = 0,4.

15. y' = xy + y²; y(0) = 0,6.

Задание 2 . Используя метод конечных разностей решить краевую задачу для обыкновенного дифференциального уравнения

Варианты:

1. ; ; .

2. ; ;

3. ; ;

4. ; ; .

5. ; ;

6. ; ; .

7. ; ; .

8. ; ;

9. ; ; .

10. ; ; .

11. ; ;

12. ; ;

13. ; ;

14. ; ; .

15. ;
Пример решения в MatLab:
Для решения систем ОДУ в MATLAB реализованы различные методы. Их реализации названы решателями ОДУ.

Обобщенное название sol ver (решатель) означает один из возможных численных методов решения ОДУ: ode45, ode23, ode113, ode15s, ode23s, ode23t , ode23tb, bvp4c или pdepe.

Решатели реализуют следующие методы решения систем дифференциальных уравнений, причем для решения жестких систем уравнений рекомендуется использовать только специальные решатели ode 15s , ode23s, ode23t. ode23tb:

ode45 — одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка. Это классический метод, рекомендуемый для начальной пробы решения. Во многих случаях он дает хорошие результаты;

ode23 — одношаговые явные методы Рунге-Кутта 2-го и 4-го порядка. При умеренной жесткости системы ОДУ и низких требованиях к точности этот мето;. может дать выигрыш в скорости решения;

ode113 — многошаговый метод Адамса-Башворта-Мултона переменного порядка Это адаптивный метод, который может обеспечить высокую точность решения

ode23tb — неявный метод Рунге-Кутта в начале решения и метод, использующий формулы обратного дифференцирования 2-го порядка в последующем

Несмотря на сравнительно низкую точность, этот метод может оказаться более эффективным, чем ode15s;

ode15s — многошаговый метод переменного порядка (от 1 до 5, по умолчанию 5), использующий формулы численного дифференцирования. Это адаптивный метод, его стоит применять, если решатель ode45 не обеспечивает решения;

ode23s — одношаговый метод, использующий модифицированную формулу Розенброка 2-го порядка. Может обеспечить высокую скорость вычислений при низкой точности решения жесткой системы дифференциальных уравнений;

ode23t — метод трапеций с интерполяцией. Этот метод дает хорошие результаты при решении задач, описывающих колебательные системы с почти гармоническим выходным сигнал;

Пример: Дано дифференциальное уравнение y^/=y-xc с начальным условием y(0)=1,5. Вычислить с точностью до =0,01 решить это уравнение при х=1,5. Вычисления провести по методы Рунге-Кутта с двумя запасными знаками.

Решение:

В М-файле с именем pr7.m пишем:

function f=pr7(x,y)

f=y-x;

end

Далее в командном окне вызываем функцию ode45

[X,Y] = ode45(@pr7,[0 1.5],1.5)

X = 0.0375

0.0750

0.1125

0.1500

0.1875

0.2250

0.2625

0.3000

0.3375

0.3750

0.4125

0.4500

0.4875

0.5250

0.5625

0.6000

0.6375

0.6750

0.7125

0.7500

0.7875

0.8250

0.8625

0.9000

0.9375

0.9750

1.0125

1.0500

1.0875

1.1250

1.1625

1.2000

1.2375

1.2750

1.3125

1.3500

1.3875

1.4250

1.4625

1.5000

Y =1.5000

1.5566

1.6139

1.6720

1.7309

1.7906

1.8512

1.9126

1.9749

2.0382

2.1025

2.1678

2.2342

2.3016

2.3702

2.4400

2.5111

2.5834

2.6570

2.7320

2.8085

2.8864

2.9659

3.0470

3.1298

3.2143

3.3006

3.3887

3.4788

3.5709

3.6651

3.7615

3.8601

3.9610

4.0644

4.1702

4.2787

4.3899

4.5039

4.6209

4.7408

plot(X,Y,'-k')

grid; Результатом будет график (см. Рисунок 8)
Р 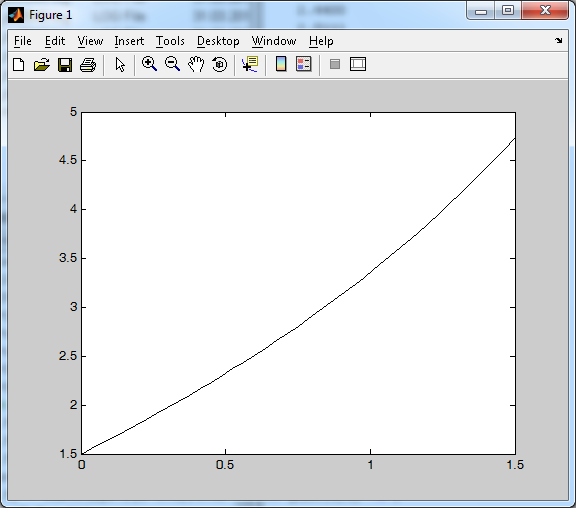исунок 8. График функции
Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.
Контрольные вопросы:

1. 
   В чем смысл краевой задачи при решении дифференциальных уравнений?
   
2. 
   В чем смысл задачи Коши с начальными условиями при решении дифференциальных уравнений?
   
3. 
   В чем суть метода Эйлера?
   
4. 
   В чем суть метода Рунге-Кутта?
   

Список использованной литературы

1. 
   MATLAB 7. Самоучитель: Е. А. Курбатова. С.-П., Вильямс, 2006 г. 256 с.
   
2. 
   Бахвалов Н.С. Численные методы. М.: Наука, 2006. 631 с.
   
3. 
   Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. 3-е изд., перераб. и доп. М.: БИНОМ. Лаборатория знаний, 2009, 632 с.
   
4. 
   Волков Е. А. Численные методы. М.: Наука, 1982.
   
5. 
   Данилина Н. И., Дубровская Н. С. Численные методы для техникумов - Высшая школа, 1976, 368 с.
   
6. 
   Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1966, 66с.
   
7. 
   Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. –М.: Наука, 1967 , 368 с.
   
8. 
   Джон Г. Мэтьюз, Куртис Д. Финк – Численные методы. Использование MATLAB. С.-П. Вильямс, 2001, 720 с.
   
9. 
   Самарский А. А. Введение в численные методы. Учебное пособие для вузов. 3-е изд., стер. СПб.: Издательство «Лань», 2005, 288 с
   
10. 
    Самарский А.А., Гулин А.В. Численные методы. М.:Наука. 1989, 430 с.