Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11

• Название: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
• Дата: 27.04.2023
• Размер: 0.72 Mb.
• Имя файла: Мет.указания по лабораторным работам.docx
• Тип: Лабораторная работа; #1093112
• страница: 11 из 14

Лабораторная работа №12.

«Аппроксимация, построение аппроксимирующих кривых»

 

Цель: научиться подбирать аппроксимирующий полином первой и второй степени и строить соответствующие аппроксимирующие кривые.
Задание:

1. 
   Подобрать аппроксимирующий полином первой и второй степени, используя метод наименьших квадратов.
   
2. 
   Используя среду MatLab подобрать аппроксимирующий полином первой, второй и третьей (если необходимо, то четвертой и т.д.) степени и построить соответствующие аппроксимирующие кривые.
   
3. 
   Найти значение функции в точке х.
   

Варианты заданий:

Вариант	xi	1	2	3	4	5	[a;b]	x
1	yi	0,7	1,9	1,1	2,2	3,5	[2;2.5]	2.2
2	yi	0,8	2,4	1,5	2,3	4,0	[5;5.8]	5.4
3	yi	2,1	3,0	1,5	3,2	4,1	[2;2.9]	2.3
4	yi	2,2	4,8	1,9	3,9	5,5	[1;2,2]	1.9
5	yi	1,0	3,5	5,0	5,6	3,8	[3;4.1]	3.8
6	yi	2,6	1,1	1,6	3,2	2,4	[4;4.3]	4.1
7	yi	3,5	4,8	3,5	1,8	1,5	[2;2.6]	2.3
8	yi	6,0	3,2	1,9	1,3	1,2	[1;1,9]	1.2
9	yi	1,5	1,8	2,5	4,0	7,0	[1;1,4]	1.1
10	yi	0	6,0	2,0	1,3	6,0	[3;3,9]	3.5
11	yi	3,5	1,2	0	1,7	2,0	[6;6,3]	6.7
12	yi	1,4	2,7	6,0	0	4,8	[4;4,7]	4.6
13	yi	2,1	3,1	5,1	5,8	6,0	[4;4,5]	4,1
14	yi	1,0	3,5	5,0	5,6	3,8	[3;4.1]	3.6
15	yi	2,6	1,1	1,6	3,2	2,4	[4;4.3]	4.2

Теоретический материал:
Аппроксимация функций с помощью метода наименьших квадратов

Метод наименьших квадратов применяется при обработке результатов эксперимента для аппроксимации (приближения) экспериментальных данных аналитической формулой. Конкретный вид формулы выбирается, как правило, из физических соображений. Такими формулами могут быть:

1. 
   Y=ax+b,
   
2. 
   Y=ax²+bx+c,
   
3. 
   Y=a_nxⁿ+a_n-1x^n-1+….+a₁x+a₀
   
4. 
   Y=ae^dx+c, y=a/x+b
   

и другие.

Пример решения в MatLab:

1. 
   Введем исходные данные
   

>> x=[1 2.2 2.4 2.7 3.1 3.5 4.5 5];

>> y=[9.054 15.077 15.754 18.3 17.984 15.852 1.772 -13.042];

2. 
   Вычислим вектор коэффициентов полинома Y=ax+b
   

>> a=polyfit(x,y,1)

a =

-5.4276 26.6479

3. 
   Вычислим значения полинома на интервале от 10 до 20
   

>> x1=0.9:0.5:5.1;

>> y1=polyval(a,x1);

4. 
   Построим график полинома и экспериментальных точек в одной графической области
   

>> plot(x1,y1,'-k',x,y,'ok')

5. 
   По графику определяем что данная кривая неподходит (см. Рисунок 5).
   
6. 
   Поэтому далее вычисляем вектор коэффициентов полинома Y=ax²+bx+c
   

>> a=polyfit(x,y,2)

a =

-4.7042 23.6773 -11.5522

7. 
   Вычислим значения полинома на интервале от 10 до 20
   

>> x1=0.9:0.5:5.1;

>> y1=polyval(a,x1);

8. 
   Построим график полинома и экспериментальных точек в одной графической области
   

>> plot(x1,y1,'-k',x,y,'ok')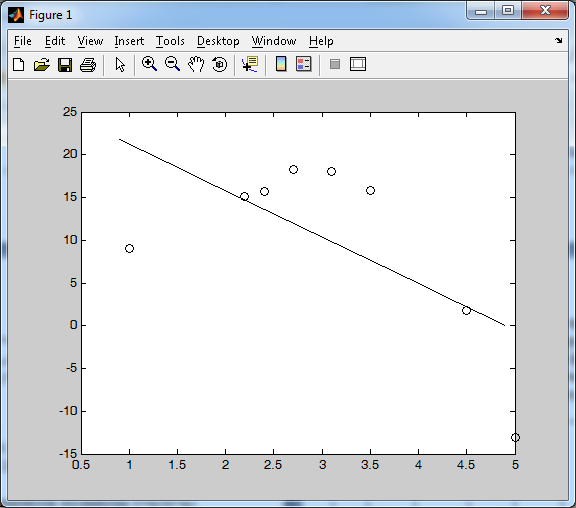

Рисунок 5. График функции

9. 
   Имеем график (см. Рисунок 6)
   
10. 
    Найдем еще вектор коэффициентов полинома Y=ax³+bx²+cх+d
    

>> a=polyfit(x,y,3)

a =

-1.3534 7.2257 -6.9270 10.0393

11. 
    Вычислим значения полинома на интервале от 10 до 20
    

>> x1=0.9:0.5:5.1;

>> y1=polyval(a,x1);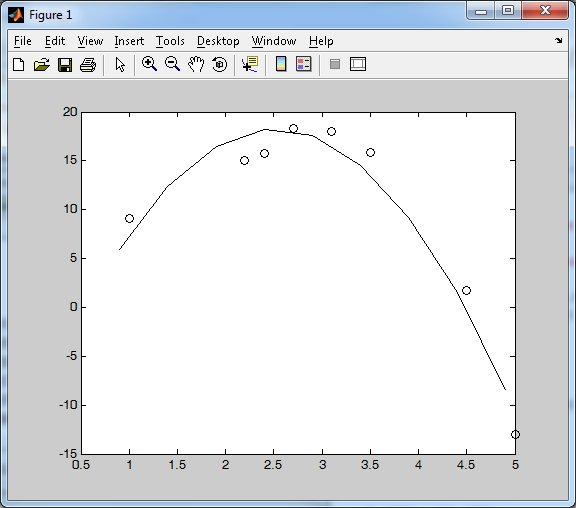

Рисунок 6. График функции

12. 
    Построим график полинома и экспериментальных точек в одной графической области
    

>> plot(x1,y1,'-k',x,y,'ok')

13. 
    Из графика (см. Рисунок 7) можно сделать вывод, что полином вида Y=ax³+bx²+cх+d является аппроксимурующей кривой для исходных данных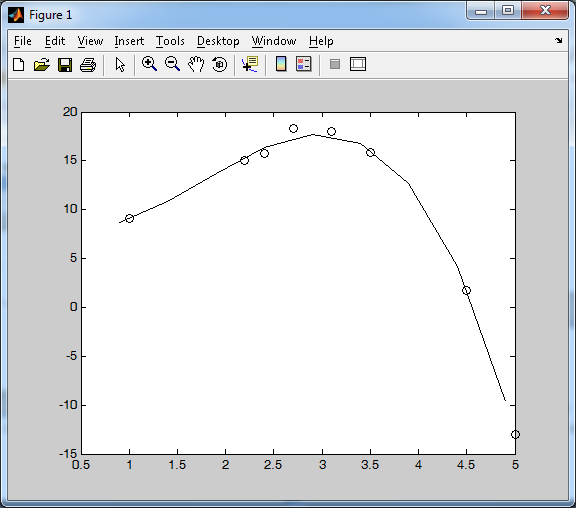
    

Рисунок 7. График функции
Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   В каком случае возникает необходимость постановки задачи аппроксимации?
   
2. 
   Сформулируйте задачу аппроксимации функции?
   
3. 
   Какая кривая называется линией регрессии?
   
4. 
   В чем заключается задача аппроксимации?
   
5. 
   Для чего используется аппроксимация функции на практике?
   
6. 
   В каком виде Вы искали линию регрессии?
   
7. 
   Для чего используется метод наименьших квадратов?
   
8. 
   Что называется аппроксимирующей кривой?