Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11

• Название: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
• Дата: 27.04.2023
• Размер: 0.72 Mb.
• Имя файла: Мет.указания по лабораторным работам.docx
• Тип: Лабораторная работа; #1093112
• страница: 12 из 14

Лабораторная работа 13.

«Численное дифференцирование функции. Методы дифференцирования»

Цель: научиться применять интерполяционные формулы численного дифференцирования для нахождения первой и второй производной функции в точках.
Задание: Найти значения производных y’ и y’’ в точках x_i. Выполнить эту задачу также в системе MatLab.
Варианты заданий:

№	xi	1	2	3	4	5	6	х
1	yi	0,7	1,9	1,1	2,2	3,5	4,1	1; 3; 5;
2	yi	0,8	2,4	1,5	2,3	4,0	4,7	2; 4; 5;
3	yi	2,1	3,0	1,5	3,2	4,1	5,3	1; 4; 6;

№	xi	0,0	0,2	0,4	0,6	0,8	1	х
4	yi	1,000	1,221	1,491	1,822	2,225	2,742	0,0 0,4 0,8
5	yi	1,002	1,210	1,500	1,842	2,236	2,812	0,2; 0,6; 0,8;
6	yi	1,003	1,230	1,495	1,853	2,257	2,356	0,0;0,4;1,0;
№	xi	-0,4	-0,2	0,0	0,2	0,4	0,6	х
7	yi	0,67	0,82	1,00	1,22	1,49	1,82	-0,4 0,0; 0,4;
8	yi	0,78	0,95	1,23	1,51	1,78	2,00	-0,2 0,2; 0,6
9	yi	0,84	1,07	1,31	1,59	1,87	2,14	-0,4 0,2; 0,4
10	yi	0,53	0,72	1,04	1,42	1,64	1,93	-0,2 0,0; 0,6

№	xi	0,5	0,6	0,7	0,8	0,9	1,0	х
11	yi	0,479	0,564	0,644	0,7174	0,7833	0,841	0,5; 0,7; 1,0
12	yi	0,944	0,645	0,326	0,4717	0,3387	0,5184	0,6; 0,8; 0,9
13	yi	0.534	0.645	0.256	0.6235	0.5126	0.158	0.1; 0,3; 0,6
14	yi	0.456	0.542	0.632	0.3256	0.2365	0.125	0,2; 0,4; 0,6
15	yi	0,78	0,95	1,23	1,51	1,78	2,00	-0,2 0,2; 0,6

Теоретический материал:

Для определения производной функции представленной виде таблицы используются формулы приближенного дифференцирования.

1. 
   Формулы приближенного дифференцирования, основанные на формулах Ньютона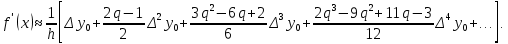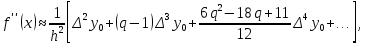
   

Что бы получить значение производной в точке, лежащей в конце таблицы, пользуются второй интерполяционной формулой Ньютона.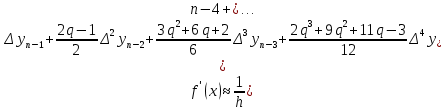

2. 
   Формулы приближенного дифференцирования, основанные на формуле Лагранжа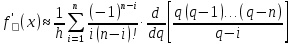
   

Произведем расчет для n=4, функция f(x) задана 5 табличными значениями. Имеем:

n = 4 (пять точек).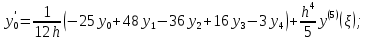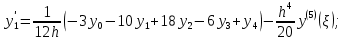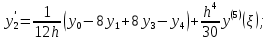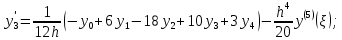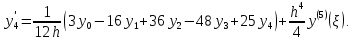











Где - точка отрезка [a, b], отличная от узлов интерполяции.

Как известно, численное дифференцирование строится на использовании аппарата конечных разностей и соответствующего многообразия аппроксимаций. Здесь полезны функции:

diff(X), diff(X, n), diff(X, n, dim) - вычисление конечных разностей (первых, n-го порядка или по указанному измерению); если Х -массив, берутся разности между столбцами:

>> F= [ 0 0.0998 0.1987 0.2955 0.3894 0.4794]

>> D=diff(F)

D = 0.0998 0.0988 0.0969 0.0939 0.0900

>> D2=diff(F,2)

D2 = -0.0010 -0.0020 -0.0030 -0.0039
Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.
Контрольные вопросы:

1. 
   Сформулируйте задачу численного дифференцирования?
   
2. 
   Запишите первую формулу Ньютона для нахождения первой производной.
   
3. 
   Запишите вторую формулу Ньютона для нахождения второй производной.
   
4. 
   Запишите формулу Логранжа для нахождения первой производной.
   
5. 
   Основные методы дифференцирования.
   
6. 
   Какой метод численного дифференцирования Вы выбрали? Почему?
   
7. 
   Численное дифференцирование для равностоящих точек, выраженные через значения функции в этих точках (формула?).
   
8. 
   Чему равна погрешность производной интерполирующей функции?
   
9. 
   Какая команда в матлабе возвращает конечные разности порядка n.