Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
Лабораторная работа №8.« Использование итерационных численных методов для решения СЛАУ»Цель: сформировать у студентов представление о итерационных численных методах решения СЛАУ, ознакомить с методом Зейделя, научить использовать данные методы с использованием MatLab. Задание: Найти для матрицы коэффициентов число обусловленности и оценить близость матрицы к вырожденной. Решить СЛАУ методом Зейделя, как в ручную, так и в MatLab. Обеспечить точность нахождения корней на уровне e=10-4. Варианты задания см. в лабораторной работе №7. Теоретический материал: Числа обусловленности матрицы определяют чувствительность решения системы линейных уравнений к погрешностям исходных данных. Следующие функции MatLab позволяют найти числа обусловленности матриц. cond(X) — возвращает число обусловленности, основанное на второй норме, то есть отношение самого большого сингулярного числа X к самому малому. Значение cond(X), близкое к 1, указывает на хорошо обусловленную матрицу; с = cond(X.p) — возвращает число обусловленности матрицы, основанное на р-норме: norm(X.p)*norm(inv(X),p), где р определяет способ расчета: р=1 — число обусловленности матрицы, основанное на первой норме(т. е. самую большую из сумм абсолютных значений элементов матрицы по столбцам.); р=2 — число обусловленности матрицы, основанное на второй норме; p= 'fro' — число обусловленности матрицы, основанное на норме Фробе-ниуса (Frobenius) norm(A, 'fro') = sqrt(sum(diag(A'A)); р='inf' — число обусловленности матрицы, основанное на норме неопределенности. Метод простых итераций довольно медленно сходится. Для его ускорения существует метод Зейделя, заключающийся в том, что при вычислении компонента 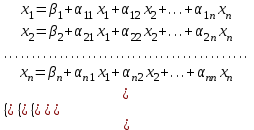 при ненулевых диагональных элементах 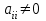 , , 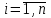 (если какой-либо коэффициент на главной диагонали равен нулю, достаточно соответствующее уравнение поменять местами с любым другим уравнением). Получим следующие выражения для компонентов вектора (если какой-либо коэффициент на главной диагонали равен нулю, достаточно соответствующее уравнение поменять местами с любым другим уравнением). Получим следующие выражения для компонентов вектора 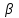 и матрицы и матрицы 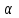 эквивалентной системы: эквивалентной системы: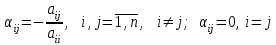 , , 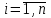 . . За начальное приближение принимается вектор правых частей 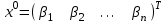 . Тогда метод Зейделя для известного вектора . Тогда метод Зейделя для известного вектора 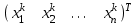 на k-ой итерации имеет вид: на k-ой итерации имеет вид: . .Пример решения СЛАУ методом Зейделя в MatLab : 1.Создадим М-фаил zeydel.m function X=zeydel(A,B,X0,delta,Imax) % Итерация Гаусса – Зейделя. % A - невырожденная матрица коэффициентов % размером n x n; % B - вектор-столбец свободных членов; % X0 - вектор-столбец начального приближения; % delta - допустимая относительная погрешность; % Imax - максимальное число итераций; % X - приближенное решение линейной системы AX = B. n=length(B); err=5*delta; X=X0; ct=0; while err>delta Xp=X; for i=1:n X(i)=(B(i)-A(i,[1:i-1,i+1:n])*… X([1:i-1,i+1:n]))/A(i,i); end if max(abs(X0))==0 error('Следует изменить начальное приближение') break end err=max(abs(X-Xp))/max(abs(X0)); ct=ct+1; Xe(ct,:)=[X' err]; if ct>Imax error('Требуемое число итераций слишком велико') break end end Xe ct 2. Далее в командной строке последовательно набираем команды, приведенные ниже. A=[ 2 -1 1; 4 -6 1; -2 1 8]; B=[2; -4; 16]; X0=[1; 2; 2]; X=zeydel(A,B,X0,1e-5,1e2) Первая из них задает матрицу коэффициентов А размером 3 на 3, вторая – вектор-столбец свободных членов В размером 3 на 1, третья – вектор-столбец начального приближения Х0 размером 3 на 1 и четвертая осуществляет запуск итерационного процесса Зейделя с заданными параметрами. 3. Полученные результаты будут представлены на экране монитора в следующем виде: Xe = 1.0000 1.6667 2.0417 0.1667 0.8125 1.5486 2.0095 0.0937 0.7695 1.5146 2.0031 0.0215 0.7558 1.5044 2.0009 0.0069 0.7517 1.5013 2.0003 0.0020 0.7505 1.5004 2.0001 0.0006 0.7502 1.5001 2.0000 0.0002 0.7500 1.5000 2.0000 0.0001 0.7500 1.5000 2.0000 0.0000 0.7500 1.5000 2.0000 0.0000 ct = 10 X =0.7500 1.5000 2.0000. Где первые три столбца матрицы Хе представляют собой приближения переменных х1, х2, х3 к решению, четвертый столбец – погрешности приближений, ct – число итераций, Х – вектор результата. Таким образом, решение системы (4.34) с относительной погрешностью 10-5 и с использованием начального приближения х(0) = [1, 2, 2] методом Гаусса – Зейделя было получено за 10 итераций. Т. е. в данном случае число итераций в процессе Гаусса – Зейделя оказалось в 1,7 раза меньше, чем при решении методом Якоби. Содержание отчета: 1. Титульный лист. 2. Цель лабораторной работы. 3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. 4. Расчетная часть: описание выполнения задания в среде MatLab. 5. Выводы и анализ полученных результатов. Контрольные вопросы: Суть метода Зейделя? В каких случаях возможно решение систем уравнений методом Зейделя? С помощью, какой функции в MatLab можно вычислить максимум функции? С помощью, какой функции в MatLab можно ввести матрицу? Что значит решить СЛАУ? Что определяет данная функции length(B)? |
