Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
Лабораторная работа №2.«Основы теории погрешностей»Цель: Научиться производить действия над приближенными величинами, вычислять погрешности результатов. Задание №1. Вычислить и определить погрешности результата. Вычисления выполнить в MatLab. Варианты заданий: 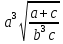 где a=72.79( где a=72.79(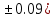 b=3.05( b=3.05(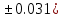 c=55.9( c=55.9(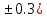  где a=3.09( где a=3.09(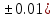 b=41.089( b=41.089(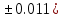 c=0.999( c=0.999(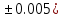 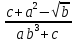 где a=13.5( где a=13.5(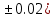 b=3.7( b=3.7( c=4.22( c=4.22(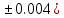 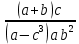 где a=34.5( где a=34.5( b=23.725( b=23.725(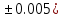 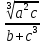 где a=3.09( где a=3.09( b=11.077( b=11.077(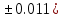 c=5.205( c=5.205(  где a=10.007( где a=10.007(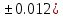 b=1.3577( b=1.3577(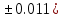 c=5.205( c=5.205( 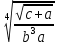 где a=35.309( где a=35.309(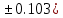 b=6.0207( b=6.0207(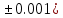 c=52.7044( c=52.7044(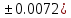 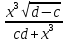 где x=13.254( где x=13.254(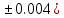 c=77.0348( c=77.0348(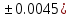 d=90.205( d=90.205(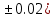 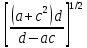 где a=0.011( где a=0.011( c=2.139( c=2.139( d=44.112( d=44.112(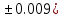  где a=3.091( где a=3.091( b=22.044( b=22.044( c=9.137( c=9.137( 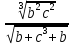 где b=104.023( где b=104.023( c=23.4567( c=23.4567(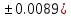  где m=32.14( где m=32.14(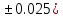 n=1.74( n=1.74(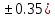 p=29.005( p=29.005( 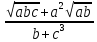 где a=65.034( где a=65.034(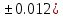 b=4.03( b=4.03( c=30.089( c=30.089(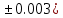 c=18.5( 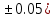 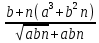 где a=27.309( где a=27.309( b=42.8( b=42.8(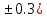 c=5.2( c=5.2( 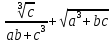 где a=5.79( где a=5.79(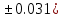 b=11.45( b=11.45(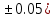 c=2.05( c=2.05(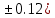 Задание №2: Выясните погрешность задания исходных данных, необходимую для получения результата с m=5 верными значащими цифрами. Вычисления провести в среде MatLab. Варианты заданий: 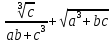 где a = 5.79 b = 11.45 c =2.05 где a = 5.79 b = 11.45 c =2.05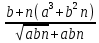 где a=27.309 b=42.8 c=5.2 где a=27.309 b=42.8 c=5.2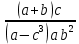 где a=34.5 b=23.725 c=18.5 где a=34.5 b=23.725 c=18.5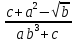 где a = 13.5 b = 3.7 c = 4 .22 где a = 13.5 b = 3.7 c = 4 .22  где a=3.09 b=41.089 c=0.999 где a=3.09 b=41.089 c=0.999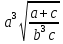 где a=72.79 b=3.05 c=55.9 где a=72.79 b=3.05 c=55.9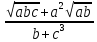 где a=65.034 b=4.03 c=30.089 где a=65.034 b=4.03 c=30.089 где m=32.14 n=1.74 p=29.005 где m=32.14 n=1.74 p=29.005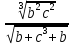 где b=104.023 c=23.4567 где b=104.023 c=23.4567 где a=3.091 b=22.044 c=9.137 где a=3.091 b=22.044 c=9.137  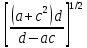 где a=0.011 c=2.139 d=44.112 где a=0.011 c=2.139 d=44.112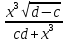 где x=13.254 c = 77.0348 d=90.205 где x=13.254 c = 77.0348 d=90.205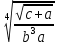 где a=35.309 b=6.0207 c=52.7044 где a=35.309 b=6.0207 c=52.7044 где a=10.007 b=1.3577 c=5.205 где a=10.007 b=1.3577 c=5.205 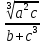 где a = 3.09 b = 11.077 c = 5.205 где a = 3.09 b = 11.077 c = 5.205Пример: Задание x= 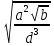 + +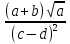 где a=2.754( 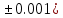 b=11.7( b=11.7(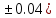 c=10.536( c=10.536( 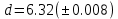 Решение Имеем:  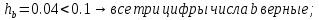 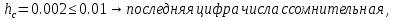 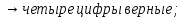 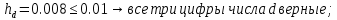 Вычислим приближенное значение выражения, применяя правила; При сложении и вычитании сохраняем столько десятичных знаков, сколько их в приближенном исходном данном с наименьшим числом верных десятичных знаков + один «запасной» При умножении и делении сохраняем столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр + одна «запасная» При возведении в степень и при извлечении корня в результате сохраняем столько значащих цифр, сколько верных значащих цифр имеет исходное число + один знак. Итоговый результат округлим до трёх значащих цифр. Первое слагаемое 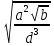 =0,32 =0,32Второе слагаемое 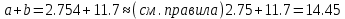 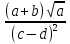 =1,349 =1,349X=1.6696  1.67 1.67Оценим погрешность результата если 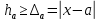   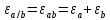 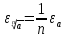 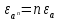 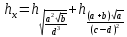 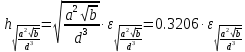 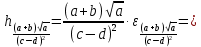 1.349 1.349 Оценим относительную погрешность первого слагаемого 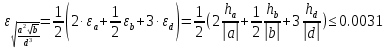 Тогда оценка абсолютной погрешности первого слагаемого 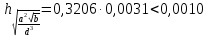 возьмем возьмем Оценим относительную погрешность вычисления второго слагаемого 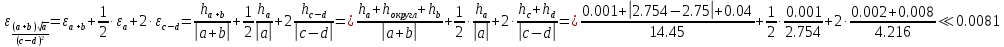 Тогда 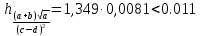 возьмем возьмем 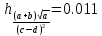 Таким образом 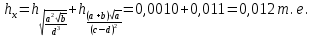 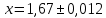 Отсюда следует, что верными являются только две цифры (0.01<0.012<0.1) Округлим результат до верных знаков : х=1,67 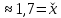 с учетом этого погрешность измениться: с учетом этого погрешность измениться: 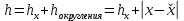 =0.012+ =0.012+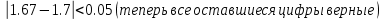 Качество вычисления составляет 100%-  Итак, окончательный ответ 1,7  Содержание отчета: 1. Титульный лист. 2. Цель лабораторной работы. 3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. 4. Расчетная часть: описание выполнения задания в среде MatLab. 5. Выводы и анализ полученных результатов. Контрольные вопросы: Как находится абсолютная погрешность приближенного числа. Как находится относительная погрешность приближенного числа. Чему равна погрешность суммы 2-х приближенных чисел? Чему равна погрешность разности 2-х приближенных чисел? Сформулируйте правило вычисления погрешности произведения 2-х приближенных чисел. Сформулируйте правило вычисления погрешности частного 2-х приближенных чисел. |
