Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
Лабораторная работа №5.«Решение систем линейных алгебраических уравнений»Цель работы: научиться вычислять корни систем линейных алгебраических уравнений различными методами. Задание 1: Решить систему линейных алгебраических уравнений с помощью: формул Крамера метода обратной матрицы. Предоставить в отчете результаты, как ручного решения, так и решение, реализованное в MatLab. Варианты заданий:
Задание 2: Решить задания с помощью: метода Гаусса LU-разложения Варианты заданий:
Пример решения СЛАУ в MatLab : Дана система уравнений: 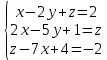 Решение системы x=A-1b A=[1 -2 1; 2 -5 -1; -7 0 1]; b=[2; -1; -2]; x=inv(A)*b Результатом будет: x = 0.5200 0.0800 1.6400 Метод Крамера: % Решим систему методом Крамера A = [1 2 3 4; -1 2 -3 4; 0 1 -1 1; 1 1 1 1]; b = [30;10;3;10]; % Проверим невырожденность системы rank(A) >> ans = 4 % По правилу Крамера A1 = A; A2 = A; A3 = A; A4 = A; A1(:,1) = b; A2(:,2) = b; A3(:,3) = b; A4(:,4) = b; x1 = det(A1) / det(A); x2 = det(A2) / det(A); x3 = det(A3) / det(A); x4 = det(A4) / det(A); x=[x1;x2;x3;x4] % Проверим решение A*x - b
Метод Гаусса: Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы, переходят к системе эквивалентной, которая решается проще, чем исходная. Метод Гаусса состоит из двух этапов: Первый этап - это прямой ход, в результате которого расширенная матрица системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на число, отличное от нуля, и сложение уравнений) приводится к ступенчатому виду. На втором этапе (обратный ход) ступенчатую матрицу преобразуют так, бы в первых n столбцах получилась единичная матрица. Последний, n +1 столбец этой матрицы содержит решение системы линейных уравнений. Порядок решения задачи в MATLAB следующий: сформировать матрицу коэффициентов Aи вектор свободных членов b заданной системы; сформировать расширенную матрицу системы, объединив A и b; используя функцию rref, привести расширенную матрицу к ступенчатому виду; найти решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте; выполнить вычисление Ax-b; если в результате получился нулевой вектор, задача решена верно. A=[1 -2 1; 2 -5 -1; -7 0 1]; b=[2; -1; -2]; C=rref([A b]); %Приведение расширенной матрицы к треугольному виду x=C(1:3,4:4)%Выделение последнего столбца из матрицы Результатом будет: x = 0.5200 0.0800 1.6400 Метод LU – разложения: Рассмотрим пример решения системы 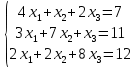 с предварительным LU-разложением матрицы. A = [4 1 2; 3 7 1 ; 2 2 8]; f = [7; 11; 12]; Выполняем LU-разложение [L, U] = lu(A); и решаем последовательно две системы с треугольными матрицами, сначала с L, затем с U y = L\f; x = U\y x = 1 1 1 Решение двух систем можно записать одним выражением x = U\(L\f) и результат получится тем же самым. Следует обратить внимание на важность использования скобок для определения порядка решения систем с треугольными матрицами. Содержание отчета: 1. Титульный лист. 2. Цель лабораторной работы. 3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. 4. Расчетная часть: описание выполнения задания. 5. Выводы и анализ полученных результатов. Контрольные вопросы: Какая функция называется аналитической? В чем заключается решение систем уравнений методом Крамера? Для каких матриц существуют обратные матрицы? В каких случаях нельзя пользоваться формулами Крамера? Суть метода Гаусса. В каких случаях возможно решение систем уравнений методом Крамера? С помощью какой функции в Матлаб можно вычислить определитель матрицы? С помощью какой функции в Матлаб можно ввести матрицу? Что значит решить СЛАУ? Какие методы решения СЛАУ Вы знаете? |
