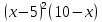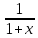Мет.указания по лабораторным работам. Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
Лабораторная работа №14.« Численное интегрирование функции»Цель работы: научиться выполнять численное интегрирование заданной функции. Задание: Выполнить численное интегрирование заданной функции f(x) в заданных пределах a, b. в системе MatLab. Использовать методы: Метод прямоугольников Метод трапеций Метод Симпсона Метод Ньютона – Котеса Оценить погрешности квадратурных формул правилом Рунге. Варианты заданий:
Методы численного интегрирования К вычислениям определенных интегралов сводятся многие практические задачи физики, химии, экологии, механики и других естественных наук. На практике взять интеграл аналитически не всегда удается. В этом случае используются методы численного интегрирования. В данной лабораторной работе рассматриваются методы Ньютона - Котеса, в частности методы прямоугольников, трапеций, Симпсона и метод Гаусса. Кроме того, в лабораторной работе рассматриваются способы аналитического и численного отыскания интегралов средствами MATLAB. Аналитическое интегрирование средствами MatLab. В лабораторной работе, основной задачей которой является исследование методов численного интегрирования, в некоторых случаях для отыскания погрешности результатов требуется точные значения интегралов. Т.е. эти величины необходимо определить аналитически. Для вычисления определенных и неопределенных интегралов в MATLAB спользуется функция int.
Пример использования функции int. В данном примере подынтегральная функция задается явным образом. Первый способ: >> a=1; >> b=1.44; >> format long e >> I=int('1+log(x)') %Неопределенный интеграл I = x*log(x) >> I=int('1+log(x)',a,b) %Определенныйинтеграл I = 72/25*log(2)+72/25*log(3)-72/25*log(5) >> I=double(I) % из символьного результата в вещественный I = 5.250860835665894e-001 % искомый результат Второй способ: >> a=1; >> b=1.44; >> syms x; >> F=2.5*x^5-6.1*x^4+3.4*x^2-9.1*x+18; >> In=int(F) % неопределенный интеграл In = 5/12*x^6-61/50*x^5+17/15*x^3-91/20*x^2+18*x >> Io=int(F,a,b) % определенный интеграл Io = 1098807919/488281250 >> I=double(Io)% из символьного результата в вещественный I = 2.250358618112000e+000 2. Теоретическая оценка погрешности численного интегрирования Рассмотрим примеры использования теоретической оценки погрешности интегрирования на примере двух задач. Пример. Определить теоретическую погрешность численного интегрирования методом трапеций в случае одного элементарного отрезка интегрирования.. Теоретическая погрешность для метода трапеций составляет В случае элементарного отрезка интегрирования, если заданы пределы интегрирования и подынтегральная функция, задачу можно решить например следующим образом: >> h=b-a; >> disp('Погрешность') Погрешность >> R=(M2*(b-a)*h^2)/12 R = 0.1164 Т.о. теоретическая оценка абсолютной погрешности погрешности составляет 0.1. 3. Численное интегрирование средствами MATLAB В MATLAB реализованы множество современных методов численного интегрирования. А. Метод трапеций. Метод трапеции реализован в MATLAB несколькими функциями: cumtrapz(у) cumtrapz(x,y) trapz(y) trapz(x,y) Наиболее интересна последняя из них. Данная функция вычисляет интеграл от функции у(х) по х методом трапеций. Аргумент и функция задаются в виде векторов или х — в виде вектора, а у — в виде матрицы. Если у(х) — матрица, то функция возвращает вектор значений интеграла для каждого столбца матрицы. Пример. Пусть подынтегральная функция имеет вид у(х) = х*еx + ln(x) + 1 Необходимо вычислить определенный интеграл в диапазоне от 1 до 10 с шагом 0.5. Решение: x=1:0.5:10; y=x.*exp(x)+log(x)+1; trapz(x,y) Решение: ans = 2.032841320958599e+005 B. Метод Симпсона. Метод Симпсона реализован в MATLAB также несколькими функциями. quad('fun', a, b) quad('fun', a, b, tol) Обозначения: 'fun'— подынтегральная функция, взятая в одинарные кавычки; а, b — пределы интегрирования; tol — относительная погрешность, задаваемая пользователем; по умолчанию tol=10-3. Пример. Вычислить интеграл от функции x+ex на отрезке [1, 2] с точностью 10-5. quad('x+exp(x)', 1, 2, 1e-5) Результат: ans = 6.170774280645000e+000 4. Правило Рунге оценки погрешности интегрирования В формулах для оценки погрешности квадратурных формул R используются значения производных подинтегральной функции, что требует дополнительного анализа и вычислений. В связи с этим получило распространение практическое правило Рунге оценки погрешности. Пусть I – точное значение интеграла, I(n) – значение интеграла вычисленное при n узлах интегрирования h = (b-a)/n, I(2n) – значение интеграла вычисленное при 2*n узлах интегрирования, h = (b-a)/2n. Необходимо определить, с какой точностью вычислен интеграл I(2n), т.е. найти абсолютную погрешность Для непосредственно определения данной погрешности необходимо найти максимум модуля соответствующей производжной от интегрируемой функции на отрезке [a, b]. Часто это достаточно трудоемкий или вообще невозможный процесс. Напрмер если интегрируемая функция задана таблично. В таких случаях оценку погрешности величины I(2n) можно провести следующим образом: Здесь m = 3 для методов средних прямоугольников и трапеций, m = 15 для метода Симпсона. Примечание. Если решается задача численного вычисления интеграла с заданной точностью, процесс удвоения числа узлов интегрирования продолжается до тех пор, пока величена не станет меньше заданной погрешности. Содержание отчета: 1. Титульный лист. 2. Цель лабораторной работы. 3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. 4. Расчетная часть: описание выполнения задания в среде MatLab. 5. Выводы и анализ полученных результатов. Контрольные вопросы: Какой метод численного интегрирования Вы выбрали? Почему? Запишите простейшие квадратурные формулы. Приведите примеры их использования. Правило Рунге оценки погрешности интегрирования? Метод трапеции реализован в MatLab функциями … Метод Симпсона реализован в MatLab функциями … Для вычисления определенных и неопределенных интегралов в MatLab используются функции … |