лекции. Лекции_МО_20. Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)

• Название: Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)
• Анкор: лекции
• Дата: 12.02.2022
• Размер: 254.78 Kb.
• Имя файла: Лекции_МО_20.docx
• Тип: Лекции; #359380
• страница: 3 из 9

. Тема 3. Симплексный метод (2 ч)

Симплексный метод является универсальным методом решения задач линейного программирования. Нам известно, что если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней ме- ре, с одним из базисных решений системы ограничений. По этому подходу требуется перебрать конечное число базисных решений и выбрать среди них то, в котором целевая функция принимает оптимальное значение.

Геометрически это соответствует перебору всех условных точек многогранника решений, однако его практическое осуществление связано с огромными трудностями, т.к. в реальных задачах число допустимых базис- ных решений достаточно велико.

Число перебираемых допустимых базисных решений можно со- кратить, если производить перебор не беспорядочно, а с учетом изменения линейной функции ,т .е. добиваясь того, чтобы каждое следующее решение было «лучше»(или, по крайней мере , «не хуже»),чем предыдущее , по значе- ниям линейной функции (увеличение ее при максимизации F , уменьшение при минимизации F).Такой перебор позволяет сократить число шагов при оптимизации. Идея последовательного улучшения решения легла в основу симплексного метода. Смысл симплексного метода состоит в последователь- ном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает луч- шее( по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение целевой функции.

Впервые симплексный метод был предложен американским уче- ным Дж. Данцигом в 1949г.

Для реализации симплексного метода необходимо освоить три

элемента:

1. 
   способ определения какого-либо первоначального допустимого ба- зисного решения;
   
2. 
   правило перехода к лучшему (не худшему) решению; 3)критерий проверки оптимальности решения.
   

Для использования симплексного метода, задача линейного про- граммирования должна быть приведена к каноническому виду .

1. 
   Максимизация линейной функции
   

Рассмотрим в качестве примера задачу об использовании ресур- сов, т.е. решить симплексным методом задачу:

F=2х₁+3х₂→max (1)

при ограничениях:

_x₁  3x₂

 18

^2x x 16

2


^ 1 2

_ x₂  5

^_3x₁  21
x₁≥0,х₂≥0 (3)

Нарисуем заданную область: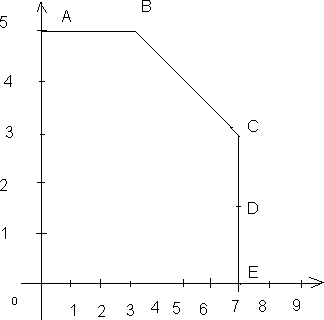

х₁

С помощью дополнительных неотрицательных переменных перехо- дим к канонической форме задач.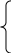
х₁+3x₂+x₃=182x₁+x₂+x₄=16х₂+x₅=53x₁+x₆=21

Для нахождения первоначального базисного решения разобьем пере- менные на две группы, основные и неосновные т.к. определитель, составлен- ный из коэффициентов при x_3,x_4, x_5,x₆отличен от нуля, т.е.

1 0 0 0 0

0 1 0 0 0

0 0 1 0 0

0 0 0 1 1

0 0 0 0 0

0

0

0 ≠ 0,

0

1

то эти переменные можно взять в качестве основных на первом шаге решения задачи. Кроме того, при выборе основных переменных на первом шаге достаточно воспользоваться следующим правилом:

В качестве основных переменных на первом шаге следует вы- брать (или возможно) также mпеременных, каждое из которых входит только в одно из m уравнений системы, при этом нет таких уравнений систе- мы, в которые не входит ни одна из этих переменных.

Дополнительные переменные удовлетворяют этому условию, по- этому их возьмем в качестве основных.

1 шаг. Основные переменные: x_3,x_4,x_5,x_6.

Неосновные переменные: x_1,x₂

Выразим основные через неосновные: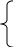

х₃=18-x₁-3x₂х₄=16-2x₁-x₂х₅=5- x₂х₆=21-3x₁

Положив неосновные переменные равными нулю, т.е. x₁=0,x₂=0, получим базовое решение:

X₁= (0;0;18;16;5;21;).

Это решение является допустимым и соответствует вершине О(0;0) многогранника FBCDE, Поскольку это решение допустимое, то оно может быть и оптимальным. Проверим это. Выразим формулу Fчерез неоснов- ные:
F=2x₁+3x₂

Видно, что формула F можно увеличить за счет увеличения любой из основных переменных, входящих в выражении F с положительным коэффи- циентом. Это можно осуществить, перейдя к такому новому дополнительно- му базисному решению, в котором эта переменная будет основной, т.е. будет принимать не нулевое, а положительное значение. При таком переходе одна из основных переходит в неосновные, а геометрически происходит переход к следующей вершине многогранника, где значение целевой функции F лучше или не хуже. В данной ситуации, для увеличения F можно переводить в ос- новные либо x₁, либо x₂, т.к. оба эти переменные входит в выражение F с плюсом, для определенности в такой ситуации выбираем переменную, име- ющую наибольший коэффициент, т.е. x₂.

Система(3) накладывает ограничения на рост переменной x₂. Посколь- ку необходимо сохранять допустимость решений, то должны выполняться следующие ограничения (при этом x₁=0 как неосновная переменная ):

^{x3  18  3x2  0}

 ¹⁸



x
_ 2 ₃

x

x



^ 4

2

_ 5

2

1
^  16  x  0





 ^x

_ 16

^  5  x  0 ^{ 2}

^^x6

 21

 _ ⁵


x


_ 2 ₁

Последнее уравнение системы не ограничивает рост переменной х₂, т.к. данная переменная в него не входит ( или формально входит с нуле- вым коэффициентом ), в этом случае условимся обозначать границу через

∞:x₂≤∞. Это же будет использоваться, когда свободный член и коэффициент при переменной в уравнении имеют одинаковый знак, т. к. и в этом случае нет ограничений на рост переменной.

Не накладывает на рост переменной, и переводимой в основные, в том случае, когда в уравнении отсутствует свободный член, т. е. он равен нулю.

Во всех этих случаях x₂≤∞.

При нулевом свободном члене и отрицательном коэффициенте при переводимой переменной уравнение ограничивает рост переменной нулем: х₂≤0.

Теперь из последней системы получаем возможное значение x₂:

х₂= min

¹⁸ ; ¹⁶ ; ⁵ =5.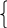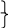

3 1 1
При x₂=5 переменная x₅обращается в нуль и переходит в число не- основных.

Определение. Уравнение, где достигается наибольшее возможное значение переменной, переводимой в основные, называется разрешающим.

В данном случае это - 3-е уравнение..

2 шаг . Основные переменные:x_2,x_3,x_4,x₆

Неосновные переменные:x_1,x₅ (x₅=5-x₂)

Выразим новые основные переменные через новые неосновные переменные, начиная с разрешающего:

^{x2  5}

^{x2  5}

x




^ ₃  18  x₁  3(5  x₅ )

x

x


или

^ ₃  3  x₁  3x₅
(4)

x


_{ 4}  16  2x₁

 (5  x₅ )

_{ 4}  11  2x₁

• 
  x₅
  

^_x₆  21  3x₁ ^_^x₆ ^{ 21  3x}₁

Второе базисное решение x₂ =(0,5,3,11,0,21) является допустимым и соответствует вершине A(0;5), т.е. осуществлен переход от вершины О к вершине А на многоугольнике решений OABCDE.

Выразим линейную функцию Fчерез неосновные переменные:

F=2x₁+3(5-x₅) =15+2x₁-3x₅

Значение линейной функции Fв т.x_2:

F₂=F(x₂)=15

Изменение значения линейной функции можно определить как произведение наибольшего возможного значение переменной, переводимой в основные (x₂), на ее коэффициент в выражении линейной функции, F:

^F=5*3=15; F₂=F₁+ ^F_, F₂= 0+15=15.
Однако значение F₂не является максимальным, т.к. в последнем вы- ражении для F имеется переменная х₁с положительным коэффициентом, что дает возможность увеличения F за счет увеличения этой переменной, т.е. пе- ременную x₁переводим в основные.

Система (4,4) накладывает ограничения на рост переменной

^x2


 5  0

x ³

1 ₁


_x₃  3  x₁  0

 x ¹¹  x mix^3 ; ¹¹; ^21  3;

x

1

3

2

 
_{ 4}  11  2x₁  0

1 ₂ 1 ^{ }

^_x₆  21  3x₁  0

_x 21

1 ₃

x₁  3 из 2-го уравнения, поэтому оно разрешающее (см. выше (4.4)), следова-

тельно переменная

^x₃ переходит в неосновные, а переменная х₁переходит в

основные переменные.
III – шаг. Основные переменные
x₁ , x₂ , x₄ , x₆ ;

Неосновные переменные

x₃ , x₅

Выразим новые основные переменные через новые неосновные (из 4):

x

^ 2

5
^{x1  3  x3  3x5} ^{x1  3  x3  3x5}

x

^ 2

5
^  5  x

^  5  x

x
(5)

x

_ 4

3
^  11  2(3  x 3x)

5

^  5  2x 5x


_ 4

3
5

_^x₆  21  3(3  x₃  3x₅ )

3. 
   е базисное решение
   

^_x₆  12  3x₃  9x₅

x₃  (3;5;0;5;12) является также допустимым и соответ-

ствует вершине

B(3;5)

многоугольника решений OABCDE. Выразим линейную

функцию Fчерез неосновные переменные:
F 2(3  x₃  3x₅ )  3(5  x₅ )  21 2x₃  3x₅

F₃  F(x₃ )  21;

(6)

Изменение значения целевой функции F:

F₂  2115  2  3  6;

И это значение

F₃  21

не является максимальным, так как в выражении

F(4.6) при x₅ имеется положительный коэффициент. Определим, насколько

можно увеличить значение этой переменной и какое уравнение является раз- решающим.

x₅  1; x₅  0

^{x1  3  3x5  0}

x 5

x

^ 2

5

5
^  5  x 0 5

x

_ 4

5
^  5  5x 0

x₅  ₅  x₅  1;

^_x₆  12  9x₅  0

_x 12

5 ₉

3. 
   е уравнение разрешающее, x₄  переходит в основные.
   

Шаг IV. Основные переменные Из (4.5).

x₁ , x₂ , x₅ , x₆ . Неосновные переменные

x₃ , x₄ .

x

_ 5

3
^  1  ² x

_ 5

• 
  ¹ x
  

₅ 4

2 1

^  1  ² x


x

_ 5

3
_ 5

1

• 
  ¹ x
  

₅ 4

3

^x 3  x

 3(1 

x x)


^x 6 

x x

_ 1 3

 <sub>2

5</sub> 3 ₅ 4 _ 1




x
₁ 

₅ 3 ₅ 4

2 1

x
^  5  (1 

_ 2



₅ x₃

 ₅ x₄ )

2 1

^  4  x

_ 2 ₅ 3

 ₃

 ₅ x₄

9

^x₆  12  3x₃  9(1  x₃  x₄

 ^{5 5}
x₄  (6;4;0;0;1;3;)

^x₆  3  x₃  x₄

 5 5

F₃  2  6  3 4  24;

Fчерез неосновные

x₃ , x_{4 :}

F 2 (6  ¹ x

₅ 3

• 
  ³ x
  

₅ 4

)  3(4  ² x

₅ 3

• 
  ¹ x
  

₅ 4

)  24  x_3;

Так как в последнем выражении функции Fнет неосновной переменной с положительным коэффициентом, то нет возможности дальнейшего увеличе- ния ее значения, т.е. максимум функции Fдостигнут:

Fmax  F₃  F(x₃ )  24;
Вывод;

при

x₁  6; x₂  4.

Прибыль предприятия принимает максимальное значение 24 $ при реализа-

ции 6 единиц продукции

P₁ и 4 единиц продукции

P_{2 .}

Критерийоптимальностиприотысканиимаксимумацелевойлинейнойфункции: