лекции. Лекции_МО_20. Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)
 Скачать 254.78 Kb. Скачать 254.78 Kb.
|
a22 x2 ... a2nxn xn2 b2 (16) ... ... ... ... ... ... ...am1 x1 am2 x2 ... amnxn xnm bm Примечание. В общем случае в системе ограничений могут быть и неравен- ства виде « ≤ » и неравенство виде « ≥». Во втором случае (« ≥ ») дополни- тельные переменные следует ввести со знаком « - ». Вопросы для контроляЧто такое экономико-математическая модель (ЭММ) задачи? Какая функция называется целевой или критериальной? Что называют планом задачи? Какой вид задачи называется стандартным? Какой вид задачи называется каноническим? Для чего используются дополнительные неотрицательные перемен- ные? В каком случае дополнительные переменные вводятся со знаком « - », и в каком случае со знаком «+»? Тема 2. Геометрический метод решения задач линейного программиро- вания (2часа)Система m линейных уравнений с n переменными. Система mлинейных уравнений с nпеременными имеют вид: a11x1 a12 x2 ... a1nxn b1 a 21x1 a22 x2 ... a2nxn b2 (1) ... ... ... ... ... ... ... am1 x1 am2 x2 ... amnxn или просто bm n aijxjj1 bi (i 1,2,..., m) В задачах линейного программирования представляют интерес системы, в которых ранг rматрицы системы A (aij),i 1, m, j 1, n, меньше числа переменных, т.е. r‹n. Предположим, что в системе (2.1) r=m, m‹n.Определение. Любые mпеременных, cистемы mлинейных уравнений с nпеременными (m‹n) называется основными(или базисными), если определитель матрицы, состоящий из коэффициентов при этих mпере- менных, отличен от нуля. Такой определитель называется базисным ми- нором матрицы А. Тогда остальные n-mпеременных называется неосновнымиили свобод-ными. Основными могут быть разные группы из mпеременных. Максимально возможное число групп основных переменных равно числу способов выбора mпеременных из n, т.е. числу сочетаний Cm. Но могут быть n случаи, когда определитель матрицы при m переменных равен нулю, тогда общее число групп основных переменных не превосходит Cm. n Пример 1. Найти все возможные группы основных переменных в систе- ме: x1 x2 2x3 x4 0 (n 4, m 2). 2x1 x2 2x3 x4 0 Решение.Общее число групп основных переменных не более чем C 2 4! 4 2!2! 12 6, 2 т.е. возможные группы основных переменных; x1 , x2 ; x1 , x3 ; x1 , x4 ; x2 , x3 ; x2 , x4 ; x3 , x4 . Выясним, могут ли быть основными переменными матрицы при этих переменных 1 1 1 2 3 0 x1 , x2 . Определитель 2 1 Следовательно, x1 , x2 могут быть основными. Поступая аналогично с другими группами, можно определить все группы основных перемен- ных. Теорема. Если для системы m линейных уравнений с n переменными (m‹n) ранг матрицы коэффициентов при переменных равен m , т.е. су- ществует хотя бы одна группа основных переменных, то это система яв- ляется неопределенной, причем каждому набору неосновных перемен- ных соответствует одно решение системы. Пусть, например, x1 , x2 ,..., xm основные переменные, т.е., определитель матрицы отличен от нуля: a11 a12 ... A a21 a22 ... a1m a2m 0 ... ... ... ... am1 am2 ... amm Оставим в левых частях уравнений системы (1) члены с основными пе- ременными x1,..., xm, а члены с неосновными переменными xm1 ,..., xn перенесем в правые части: a11x1 a12 x2 ... a1mxm b1 a1,m1 xm1 a1,m2 xm2 ... a1nxn ax a x... a x b a x a x ... a x 21 1 22 2 2m m 2 2,m1 m1 2,m2 m2 2n n ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... am1 x1 am2 x2 ... ammxm bm am,m1 xm1 am,m2 xm2 ... amnxn Задавая неосновным (свободным) переменным xm1 ,..., xn произволь- ные неотрицательные значения, каждый раз будем получать новую си- стему с новыми свободными членами b' ,b' ,...,b' . Каждая из полученных 1 2 m систем будет иметь один и тот же определитель A 0 , следовательно, каждая из этих систем будет иметь единственное решение. Т.к. получае- мых таких систем много, то и система (1) будет иметь бесконечное мно- жество решений. Пример 2. Решить систему уравнений: x1 x2 2x3 x4 0 2x1 x2 2x3 x4 0 Решение. Выше установили, что переменные основными, поэтому возьмем их в качестве основных. x1 , x2 могут быть Тогда переменные x3и x4являются неосновными ( свобод- ными).Члены с неосновными переменными перенесем в правую часть системы. 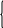 х1-x2=2x3-x42x1+x2=-2x3+x4+2 х1-x2=2x3-x42x1+x2=-2x3+x4+2Решая эту систему любым способом, получим:  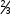 х1= х1=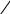 х2=23 -2x3-x4 х2=23 -2x3-x4Задавая неосновным переменным х3,х4произвольные зна- чения, например, x3=c1и x4=c2,получим бесконечное множество решение этой системы: 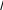  х1=2 3 х1=2 3 х2=2 3 -2c1+c4 х2=2 3 -2c1+c4Решение x=(x1…,xn )системы (1) называется допустимым , если оно содержит лишь неотрицательные компоненты, т.е.xj 0,j=1,n. В противном случае решение называется недопустимым. Так в данной задаче решение системы при c1=2,c2=5,получим x=(2/3;5 ;2;5)является 3  допустимым, а при c1=2,c2=1,x=( 2 3 ;- 7 ;2;1) является недопустимым. допустимым, а при c1=2,c2=1,x=( 2 3 ;- 7 ;2;1) является недопустимым.3 Определение. Базисным решением системы m линейных урав- нений с nпеременными называется решение, в котором все n-mнеос- новных переменных равны нулю. Допустимые базисные решения еще называются опорными. Число базисных решений конечное, т.к. оно равно числу груп- пы основных переменных, не превосходящему Cm.Базисное решение, n в котором хотя бы одна из основных переменных равна нулю, называ- ется вырожденным. Пример 3. Найти все базисные решения системы, приведенной выше. Решение. Было установлено, что существует три группы основ- ных переменных x1,x2;x1,x3;x1,x4, т. е, число базисных решений рав- но трем.  Основные переменные - x1,x2, неосновные переменные - x3,x4. Основные переменные - x1,x2, неосновные переменные - x3,x4.x1-x2=0 x1=x22x1+x2=2 x2=2\3,x1=2/3 Первое базисное решение Х1=(2/3;2/3;0;0) допустимое.  Основные переменные x1,x3; неосновные переменные x2,x4x1-2х3=0 x1=2x3 Основные переменные x1,x3; неосновные переменные x2,x4x1-2х3=0 x1=2x32x1+2x3=2 6x3=2; x3=1 ; x1=2 3 3 е базисное решение Х2=(2/3;0;1/3;0) . Основные переменные x1,x4;  Неосновные переменныеx2,x3.x1+x4=0 x1= -x4 Неосновные переменныеx2,x3.x1+x4=0 x1= -x42x1-x4=2 -2x4-x4=2;x4=-2 ;x1=2 3 3 е базисное решение Х3=( 2 ;0;0;- 2 ) является недопустимым 3 3 решением. Выпуклые множества точек Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки.    Примеры: Примеры:Теорема.Пересечение (общая часть) любого числа выпуклых множеств также есть выпуклое множество. Среди точек выпуклого множества можно выделить внут- ренние, граничные и угловые точки. Точки являются внутренней, если в некоторой ее окрестности содержатся точки только данного множества. Точка множества называ- ется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему. Особый интерес в линейном программировании вызывают угловые точки. 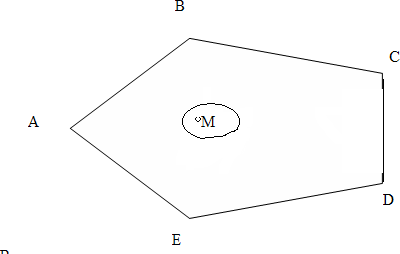 Точка множества называется угловой (или крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего множеству. Точка множества называется угловой (или крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего множеству.Если множество есть многоугольник, то его вершины являются угло- выми точками. Выпуклое замкнутое множество точек пространства (плоскости), имеющее конечное число угловых точек, называются выпуклым многогран- ником (многоугольником), если оно ограниченное и выпуклой многогранной (многоугольной) областью, если оно неограниченное. Мы рассмотрим выпуклые множества точек на плоскости и в пространстве, т.е. такие точки изображаются парой чисел (x1,x2).или тройкой чисел(x1,x2,x3).Теперь обобщим это понятие для n - мерных то- чек (x1,x2,…,xn). Обобщением понятия отрезка для нескольких точек яв- ляется их выпуклая комбинация. Определение. Точка Xназывается выпуклой линейной комбина- цией точек x1,x2,…,,xn, если выполняется условие: n X= 1x1+ 2x2+….+ nxn, j 0,j=1,2…,n, a 1 j1 В частном случае, при n=2 выпуклой линейной комбинацией двух точек является соединяющий их отрезок. Определение выпуклого множества любой размерности: Мно- жество точек является выпуклым, если оно с любыми двумя точками со- держит их произвольную множественную линейную комбинацию. Свойства задачи линейного программирования Нами были рассмотрены различные формы задачи линейно- го программирования. Сейчас рассмотрим задачу линейного про- граммирования в канонической форме, в которой систем ограниче- ний есть система уравнений. Остановимся на двух видах записи ка- нонической задачи. F c1x1 c2 x2 ... cnxn max при ограничениях a11x1 a12x2 ... a1nxn b1 (min) (1) ax a x ... a x b (2) 21 1 22 2 2n n 2 ... ... ... ... ... ... ... am1 x1 am2 x2 ... amnxn bm. Матричная форма записи F=C·X max (min) (3) при ограничениях AX=B, (4) X 0. (5) где С=(с1,с2,…,сn), a ... a x1 b1 11 1n x b A a21 ... ... ... ... a2n , 2 X . , B 2 . . a ... ...a x b m1 mn n m Теорема . Если задача линейного программирования имеет оптималь- ное решение, то целевая функция принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если целевая функция принимает максимальное (минимальное) значение более чем в од- ной угловой точке, то она принимает его в любой точке, являющейся выпук- лой комбинацией этих точек. Будем в дальнейшем полагать, что многогранник решений явля- ется ограниченным. Данная теорема позволяет значительно сократить работу по отысканию оптимального решения, т. к. благодаря ей требуется всего лишь исследовать угловые точки многогранника решений. Геометрическийметод решения задачлинейногопрограммирования Геометрический метод удобен при n=2или n=3.Нам известно, что множество допустимых решений (многогранник решений) задачи линейного программирования представляет собой выпуклый много- гранник, а оптимальное решение задачи находится в одной из угловых точек многогранника. Геометрический метод имеет два подхода: Определить координаты каждой вершины многогранника реше- ний. Определить значение целевой функции в каждой из вершин, тогда станет известно, в какой достигается минимальное значе- ние целевой функции, если задач на минимизацию, и в какой находится максимальное значение целевой функции в случае максимизации целевой функции. Решение задачи производится с помощью так называемой линии уровня. Определение. Линия уровня функции - это линия, на которой данная функция имеет постоянное значение.Покажем, как используются линии уровня при решении за- дачи линейного программирования. Рассмотрим задачу в стан- дартной форме с двумя переменными: F при c1x1 c2 x2 max (min) (1) a11x1 a12x b1 (2) a21x1 a22x2 b2 и x1 0, x2 0 (3) При n>m,к такой форме может быть приведена и задача в основной форме. Пусть в геометрическом изображении системы ограничений есть многоугольник ABCDE: 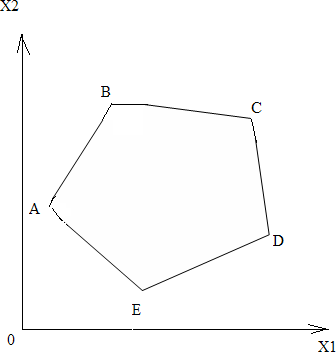 Пример. Решить геометрически задачу: 2x1+3x2 max при ограничениях:  x1+3x2 18 x1+3x2 182x1+ x2 16 х2 5, 3x1 21,х1≥0,х2≥0. 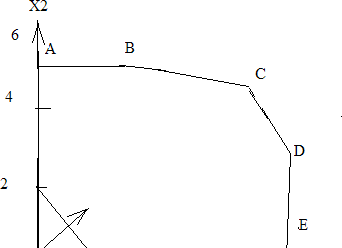 Данные ограничения геометрически образуют следующую область: Данные ограничения геометрически образуют следующую область:Пусть начальная линия уровня F 2x1 3x2 0. , т.е. она проходит через начало координат. Теперь зададим, например, F=6,и построим линию уровня 2x1 3x2 6 . Ее расположение указывает на направление возрастания линей- ной функции F . Так как мы находим максимум F ,то оптималь- ное решение находится в угловой точке С, являющейся пересечением прямых I и II, ее координаты определяются решением системы: x1 3x2 2x1 x2 18 16 x1 18 3x2 36 6x2 x2 16 x1 6, x2 4 Максимум Fпри этом Fmax 2 6 3 4 24 . Вопросы для контроляЧто такое ранг матрицы? Какие переменные называются основными (базисными)? Какие переменные называются неосновными (свободными)? Что такое допустимое решение задачи линейного программирова- ния? Какое решение называется базисным? Какое решение называется вырожденным? Среди каких решений находится оптимальное решение задачи ЛП? Что такое многогранник решений? Где находятся базисные решения задачи ЛП относительно много- гранника решений? Какая область является выпуклой? В каких случаях удобно пользоваться геометрическим методом решения задач ЛП? Что такое линия уровня? В какой точке многогранника (многоугольника) решений нахо- дится оптимальное решение задачи ЛП? Как можно найти направление возрастания (убывания) целе- вой линейной функции? |
