лекции. Лекции_МО_20. Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)

• Название: Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)
• Анкор: лекции
• Дата: 12.02.2022
• Размер: 254.78 Kb.
• Имя файла: Лекции_МО_20.docx
• Тип: Лекции; #359380
• страница: 7 из 9

Тема 6. Транспортная задача. Общие положения (2 часа)

1. 
   Экономико-математическая модель транспортной задачи (ТЗ).
   

Т3 является важным частным случаем задачи линейного программирования.

Пример. Имеются три поставщика и четыре потребителя. Мощность постав- щиков и спрос потребителей, а также затраты на перевозки единицы груза для каждой пары «поставщик- потребитель» приведены в следующей табли- це:

По- ставщи- ки	Мощность поставщи- ков	Потребители и их спрос
		1		2		3		4
		20		110		40		110
1	60	1	x11	2	x12	5	x13	3	x14
2	120	1	x21	6	x22	5	x22	2	x24
3	100	6	x31	3	x32	7	x33	4	x34

В левом верхнем углу произвольной

(i, j)

клетки ( i- номер строки,

j - номер столбца) стоит так называемый коэффициент затрат - затраты на перевозки единицы груза от i -го поставщика к j -му потребителю, для при- мера возьмем клетку (2,3): затраты на перевозку единицы груза от 2-го по- ставщика к 3-му потребителю составляет 5 денежных единиц.

Задача ставиться следующим образом:

Найти такие объемы перевозок для каждой пары «поставщик- по- требитель» так, чтобы:

1. 
   Мощности всех поставщиков были реализованы;
   
2. 
   Спросы всех потребителей были удовлетворены;
   

3. 
   Суммарные затраты на перевозку были минимальны.
   

Решение. Построим экономико-математическую модель задачи.

Пусть

^x_ij- искомый объем перевозки от i-го поставщика к j-у потреби-

телю, назовем его поставкойклетки ( ^{i, j}).

Заданные мощности поставщиков и спросы потребителей накладывают

ограничения на значения неизвестных

^xij^.

Например, объем груза, забираемого от 1-го поставщика, должен быть равен мощности этого поставщика – 60 единицам т.е.

x₁₁  x₁₂  x₁₃  x₁₄  60

Это есть уравнение баланса по первой строке. Аналогично рассуждая для 2-го и 3-го поставщиков, получим:

^{x11  x12  x13  x14  60}

x


^ 21

_x

 x₂₂

• 
  x
  

 x₂₃

• 
  x
  

 x₂₄

• 
  x
  

 120

 100

(1)

 ^{31 32}

33 34

Также спрос каждого потребителя должен быть удовлетворён, поэтому подобные уравнения баланса составляем для каждого столбца таблицы:

<sup>x11  x21  x3120

</sup>x  x  x  110

^ 12 22 32

(2)

^x  x  x

 40

_ 13 23 33

^_x₁₄  x₂₄  x₃₄  110

Очевидно, объем перевозимого груза не может быть отрицательным, поэтому

x_ij 0,

i 1,2,3,

j 1,2,3,4.

Суммарные затраты F на перевозку выражаются через коэфиценты за- трат и поставки следующим образом:

F 1 x₁₁  2  x₁₂  5x₁₃  3x₁₄ 

 1 x₂₁  6x₂₂  5x₂₃  2x₂₄ 

 6  x₃₁  3x₃₂  7x₃₃  4x₃₄
(3)

Теперь можно дать математическую формулировку следующим обра- зом:

На множества решений системы ограниченной (1) и (2) найти такое

решение

x (x₁₁, x₁₂

,...,

^x₃₃^{, x}₃₄ ⁾ , при котором линейная функция (3)

имеет минимальное значение.

Теперь дадим математическую формулировку для общего вида. Пусть ^m- число поставщиков, ⁿ- число потребителей; Обозначим

через

C_ij- коэффициенты затрат,

i 1, ..., m,

j 1, ...,

^n, через

M_i- мощ-

ности поставщиков, N_j- спросы потребителей. Тогда системы ограни-

чений примет следующий вид:

n

 ^xij

j1


m




 ^xij

i1

 M_i,
 N_j,

i 1,2, ..., m
j 1,2, ..., n

(4)
(5)

Линейная функция имеет следующий вид:

F _

j1




i1

^Cij^Xij
(6)

Формулировка в общем виде:

На множестве неотрицательных (допустимых) решений системы огра-

ничений (4) и (5), найти такое решение

x (x_11, x₁₂

,..., x_ij

^{,..., xmn)} , при ко-

тором значение линейной функции Fминимальное.

Произвольное допустимое решение x (x₁₁, x₁₂ ,..., x_ij,..., x_mn) системы

ограничений (4) и (5) называется распределением поставок. Рассмотренная на примере транспортная задача (Т3)обладает важной особенностью: суммарная мощность поставщиков равна суммарной мощности потребителей:

m n

 ^Mi^  ^Nj

(7)

i1 j1

Такие Т3 называется закрытыми, а ее модель закрытой моделью. В противном случае Т3 называется открытой и ее модель открытой мо-делью.

Мы будем рассматривать только закрытые Т3.

Так как Т3 является задачей линейного программирования, то ее также можно решить симплексным методом (СМ). Однако имеющиеся в Т3особенности позволяют существенно упростить СМ. Приведем особен- ности Т3:

1. 
   Система ограничений есть система уравнений, т.е. Т3задается в ка- нонической форме;
   
2. 
   Коэффициенты при переменных системы ограничений равны еди- нице или нулю;
   
3. 
   Каждая переменная входит в систему ограничений два раза – один раз в систему (1), и один раз в систему (2).
   

Модификация СМ применительно к Т3называется распределитель-нымметодом.

И в этом случае решение осуществляется по шагам, и каждому шагу соответствует разбиение переменных на основные (базисные) и не- основные (свободные).

Число rосновных переменных Т3 равно рангу системы линейных уравнений.

Имеет место следующая теорема:

Ранг rсистемы уравнений (4) и (5) при условии (7) равен m n1.

Основное следствие этой теоремы заключается в следующем: Число

rосновных (базисных) переменных закрытой Т3равна m n1, где

m- число поставщиков, n- число потребителей. Каждому разбиению

переменных

^xij

задачи на основные (базисные) и неосновные (сво-

бодные) соответствует базисное решение и, как следствие, заполне- ние таблицы поставок, которое также называется базисным.

Иначе говоря, распределение поставок называется базисным, если переменные, соответствующие заполненным клеткам, можно при- нять за основные переменные.

Клетки, соответствующие заполненным клеткам, называется базис-ными, а также соответствующие свободным переменным, называет- ся свободными или пустыми (базисная клетка – заполненная клет- ка). Подобно тому, как это было в СМ, в распределенном методе решения Т3, будем переходит от одного распределения поставок к другому в сторону не возрастания линейной целевой функции вплоть до оптимального решения. Для начала такого движения по- требуется нахождения первоначального базисного распределения поставок, которое называется еще опорным планом.

Примеры.

^{x11  x12  x13  50}

x


^{1. } 21

_x

 x₂₂

• 
  x
  

 x₂₃

• 
  x
  

 70

 60

(1)

 ^{31 32 33}

^{x11  x21  x31  60}



12

22

32
^x  x  x  60

(2)

^x  x  x  50

 ^{13 23 33}

F 2x₁₁  3x₁₂  2x₁₃  2x₂₁  4x₂₂  5x₂₃ 

 6x₃₁  5x₃₂  7x₃₃  min

x₁₁  0, x₁₂  0,..., x_ij 0,..., x₃₃  0.

2. 
   Нахождениепервоначальногобазисногорешения распределенияпоставок
   

1. 
   Метод северо – западного угла.
   

Одним из методов нахождения северо-западного угла является пра- вило «северо-западного угла». Вернемся к примеру.

Дадим переменной х₁₁, которая находится в северо-западной клетке таблицы, максимально возможное значение:

х₁₁=min{60,20}=20.

После этого потребности первого потребителя будет полностью удо- влетворены, в результате 1-й столбец исключается из рассмотрения (запол- ненные клетки будем перечеркивать сплошной линией, а клетки, выпавшие из рассмотрения, пунктирной линией).

Затем в оставшейся части таблицы находим новый северо-западный угол – клетку (1,2) и дадим ей максимально возможное значение, с учетом того, что первый поставщик отдал уже 20 единиц груза и у него осталось только 40 единиц груза, получаем

x₁₂  min{40,110}  40.

После этого мощность 1-го поставщика полностью реализована и из рассмотрения исключается 1-я строка таблицы поставок.

В оставшейся таблице снова находим «северо- западный» угол:

x₂₂  mix120,110  40 70.

Новый северо-западный угол:

x₂₃  120  70; 40 40.

Исходя из уже заполненных клеток, однозначно получим, что х₂₄=10 и х₃₄=100.

В результате получаем следующее распределение поставок: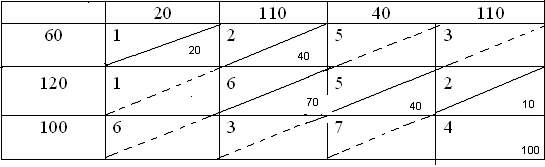


Как утверждалось в теореме, число заполненных клеток оказалось равным:

m n1  3  4 1  6

т.е. числу основных (базисных) переменных, следовательно получен- ное первоначальное распределение поставок является базисным.

2. 
   Метод наименьших затрат.
   

Существующий недостаток метода северо-западного угла состоит в том, что он построен без учета коэффициентов затрат задачи и при этом тре- буется большее число шагов для нахождения оптимального решения. Метод наименьший затрат позволяет быстрее найти оптимум задачи.

Рассмотрим опять исходную задачу.

Находим в таблице поставок клетку с наименьшим коэффициентом затрат. Таких имеется 2 клетки - (1,1) и (2,1) с коэффициентом затрат 1.

Сравним максимально возможные поставки для них:

x₁₁  min 60,20 20;

x₂₁  min 120,20 20.

Так как они совпадают, то максимально возможную дадим в любую из них. Например, в клетку (2,1).

В результате спрос 1-го удовлетворен, 1-й столбец исключается из дальнейшего рассмотрения. В оставшейся таблице находим клетку с наименьшим коэффициентом затрат, таких два C₁₂  C₂₄  2;

Сравним максимальные возможные поставки этих клеток:

x₁₂  min 60,110 60;

x₂₄  min 120  20,110  100.

Даем поставку в клетку (2,4), для которой максимально возможная поставка оказалось больше. 2-я строка исключается, из оставшейся части находим клетку с наименьшим коэффициентом затрат - клетка (1,2):

x₁₂  min 60,110 60

x₃₄  min 100  50;110

Таким образом, получим следующее распределение поставок:

	20	110	40	110
60	1	2 60	5	3
120	1 20	6	5	2 100
100	6	3 50	7 40	4 10

Теорема. Пусть на каждом шаге заполнения таблицы поставок воз- никает одна заполненная клетка, причем из рассмотрения на каждом шаге (кроме последнего) исключается либо одна строка, либо один столбец. Тогда переменные, соответствующие заполненным клеткам, можно принять за ба- зисные.

Примечание. Методы северо-западного угла и наименьших затрат приводят к базисным распределениям поставок, если на каждом (кроме по- следнего) шаге из рассмотрения выпадает либо одна строка, либо один стол- бец.

Рассмотрим особые случаи, когда на некотором шаге заполнения из рассмотрения выпадают одновременно и строка и столбец. Покажем, как следует поступать в таких случаях.

Рассмотрим следующую Т3:

20

10

40

30	1 20	3 10	5
30	3	3	3 30
10	4	1	2 10

1. 
   Северо-западный угол
   

x₁₁  min30, 20 20.

x₁₂  min 10,10 10

При этом из рассмотрения выпадают и 2-й столбец, и 1-я строка.

Таким образом, мы получили заполненную таблицу, т.е. распределе- ние поставок. Но число заполненных клеток 4 оказалось меньше, чем m n1  3  3 1  5, т.е. меньше числа базисных переменных.

Такое распределение не является базисным.

Чтобы избежать этого, используем искусственный прием.

Разобьем II-шаг на два шага. Допустим, что после поставки в клетку (1,2) из рассмотрения выпадает, например, только 1-я строка.

(Аналогично можно взять и 2-й столбец).

	20	10	40
30	1 20	3 10	5
30	3	3 0	2 30
10	4	1	2

10

Для того, чтобы вывести из рассмотрения 2-й столбец делаем еще один шаг: даем нулевую (фиктивную) поставку в произвольную, но не вы- черкнутую клетку 2-го столбца, например, в клетку (2,2). Далее действуем как обычно и получаем последнюю таблицу.

Клетки, перечеркнутые сплошной чертой, отвечающие базисным пе- ременным, в дальнейшем назовем заполненными, несмотря на то, что среди них есть клетки с нулевыми поставками. Этот прием можно использовать и при методе наименьших затрат.