лекции. Лекции_МО_20. Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)
 Скачать 254.78 Kb. Скачать 254.78 Kb.
|
Тема 8. Транспортная задача. Распределительный метод решения транспортной задачи (2 ч)Распределительный метод Алгоритм решения закрытой Т3 излагается следующим образом: Нахождение первоначального распределения поставок. Проверка критерия оптимальности очередного распределения поста- вок. Для данного базисного распределения поставок подбираем потенциалы строк и столбцов таблицы поставок так, чтобы коэффициенты затрат запол- ненных клеток стали равной нулю. Если оценки всех свободных клеток неотрицательны, то найденное решение оптимальное – решение закончено. Если среди оценок свободных клеток есть отрицательные, то выбираем одну из них для передачи в нее поставку (для определенности можно брать, например, одну из клеток с наименьшей оценкой). Для выбранной свободной клетки строится означенный цикл пересче- та. Поставка Z, передаваемая по циклу, определяется как минимум среды поставок в клетках цикла со знаком «-» . Найденная поставка передвигается по циклу, увеличивая поставки в клетках со знаком «+» на Z и уменьшая по- ставки в клетках со знаком «-» на Z. Клетка с поставкой, которой при этом станет равной нулю, будет считаться свободной, а остальные клетки заполненными. Т.е. получено новое базисное распределение поставок. Переходим к п. 2 алгоритма. При решении Т3 могут возникнуть следующие особые случаи: В некоторых случаях поставка, переводимая по циклу, может оказаться рав- ной нулю. Это возможно тогда, когда клетка цикла со знаком “ –“ содержит нулевую поставку. В этом случае по циклу передается нулевая поставка. В результате та свободная клетка, для которой был построен цикл пересчета, становится заполненной нулевой поставкой, а клетка с нулевой поставкой свободной. Если при переводе поставки по циклу поставка обращается в нуль сразу в нескольких свободных клетках, то свободной из них можно считать только одну любую из них, а остальные считать заполненными нулевой поставкой.  Рассмотрим пример: Рассмотрим пример:
Чтобы проверить выполнение критерия оптимальности, находим оценки свободных клеток по указанному ранее второму правилу в предыдущей теме: 1 3 3 0 0 0 3 3 3 2 2 0 0 4 4 2 2 0 В этом случае можно было одновременно прибавлять к элементам 1-го столбца -1, к элементам 2-го столбца -3, а к элементам 3-го столбца -2. В полученной матрице оценок в одной свободной клетке, а именно в клетке (3,2) имеется отрицательное значение, поэтому полученное базисное распре- деление поставок не оптимально. Переведем поставку именно в эту клетку. Построим для клетки (3,2) означенный цикл:  
(2,2) (2,3) (3,2)  Передаваемая поставка определяется как минимум среди поставок клеток цикла со знаком “ –“ Передаваемая поставка определяется как минимум среди поставок клеток цикла со знаком “ –“Передавая по циклу нулевую поставку, получим новое базисное распределе- ние поставок.
Проверим оптимальность полученного распределения поставок. Определение оценок свободных клеток : 1 3 3 1 2 1 1 0 1 0 0 1 3 3 2 3 2 0 3 2 0 4 2 0 4 5 4 4 1 2 0 0 0 0 0 0 Критерий оптимальности не выполнен. В клетке (1.3) имеется отрицатель- ный элемент. Дадим поставку в эту клетку. Означенный цикл для этой клет- ки: 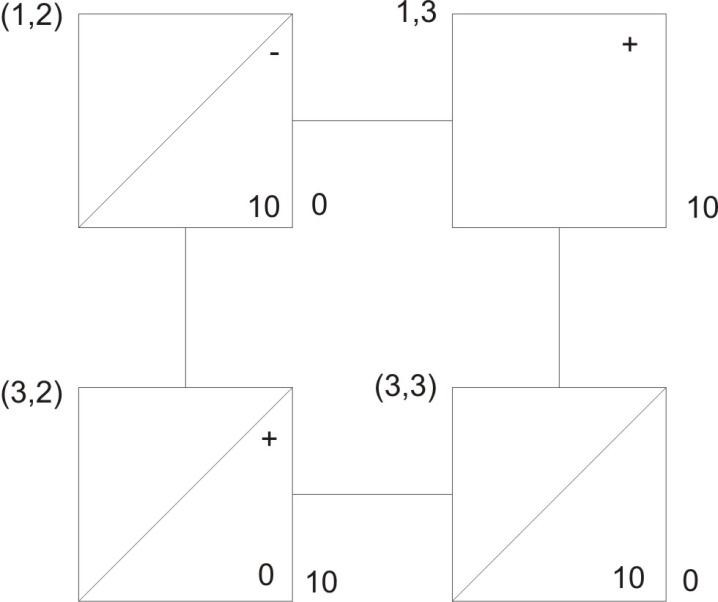  Получим следующее распределение поставок Получим следующее распределение поставок
Проверяем на оптимальность полученное решение: 1 3 3 0 2 2 0 2 0 0 0 0 0 0 0 3 3 2 3 3 2 3 3 0 3 1 0 3 1 0 4 4 4 4 5 1 2 1 2 1 0 1 0 0 0 Так как все оценки свободных клеток неотрицательны, полученное распреде- ление поставок является оптимальным. Оптимальные поставки имеют вид: х11=20ед.,х13=10ед.,х23=30ед.,х32=10 ед.груза. Минимальные расходы для доставки этих поставок: Fmin=1∙20+3∙0+3∙10+2∙30+1∙10=120д.е. Открытыетранспортныезадачи Как нам известно, в закрытых транспортных задачах суммарная мощность поставщиков равна сумме спросов потребителей. Если суммарная мощность поставщиков не равна сумме спросов потребителей, то такая транспортная задача называется открытой транспортной задачей. В этом случае открытая транспортная задача решается приведением ее к закрытой транспортной задаче. Возможны два случая: Суммарная мощность поставщиков больше суммы спросов потребите- лей. В этом случае вводится дополнительный фиктивный потребитель, спрос которого равен разности между суммарной мощностью постав- щиков и суммой спросов потребителей. Таким образом. получится за- крытая транспортная задача. Суммарная мощность поставщиков меньше суммы спросов потребите- лей. В этом случае вводится дополнительный фиктивный поставщик, мощность которого равен разности между суммой спросов потребите- лей и суммарной мощностью поставщиков. И в этом случае получится закрытая транспортная задача. Рассмотрим это подробно на следующем примере.
В данной задаче суммарная мощность поставщиков равна 30+7+70= 170 ед. груза, а сумма спросов потребителей составляет 50+50+40+60= 200 ед. груза. Сумма спросов потребителей превышает суммарной мощности поставщиков на 30 ед. груза. Поэтому введем фиктивного поставщика с мощностью 30 ед. груза. В результате получим закрытую транспортную задачу. Аналогично можно привести открытую транспортную задачу с лишней мощностью по- ставщиков введением фиктивного потребителя со спросом, равным этой лишней мощности, и также получим закрытую транспортную задачу. Далее полученная закрытая транспортная задача решается известным нам распре- делительным методом. Вопросы для контроляРасскажите алгоритм распределительного метода. Как строится означенный цикл пересчета? Как определяется передаваемая по циклу поставка? Когда выполняется критерий оптимальности распределения поста- вок? Как следует поступить, если передаваемая поставка равна нулю? Как поступить, если в означенном цикле пересчета сразу в несколь- ких клетках поставки превращаются в нуль? Какая транспортная задача называется открытой транспортной за- дачей? Как решается открытая транспортная задача? Чему равна мощность фиктивного поставщика? Чему равен спрос фиктивного потребителя? ЛитератураАзарнова Т.В., Каширина И.Л., Чернышова Г.Д. Методы оптимизации: Учебное пособие. – Воронеж: Издательство ВГУ, 2003. – 86 с. Под ред. Кремера Н.Ш. Исследование операций в экономике: Учебное по- собие.- М.: ЮНИТИ, 1999. – 407 с. Акулич И.Л. Математическое программирование в примерах и задачах: Учебное пособие для студентов экономических специальностей вузов. – М.: Высшая школа, 1986. – 318 с Алексеев В.М., Галлеев Э.М., Тихомиров В.М. Сборник задач по оптими- зации. Теория. Примеры. Задачи. Учебное пособие. – М: Наука. Главная ре- дакция физико-математической литературы, 1984. – 288 с. Ашманов С.А. Линейное программирование – М: Наука. Главная редакция физико-математической литературы, 1981. – 340 с. Глебов Н.И., Кочетов Ю.А., Плясунов А.В. Методы оптимизации: Учебное пособие / Новосибирский университет – Новосибирск 2000. – 104 с. Интрилигатор М. Математические методы оптимизации и экономическая тория. - М.: Прогресс, 1975. – 604 с. Канторович Л.В., Горстко А.В. Математическое оптимальное программи- рование в экономике. – М.: Знание, 1968. – 96 с. Канторович Л.В., Горстко А.В. Оптимальные решения в экономике. – М.: Наука, 1972. – 232 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
