лекции. Лекции_МО_20. Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)

• Название: Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)
• Анкор: лекции
• Дата: 12.02.2022
• Размер: 254.78 Kb.
• Имя файла: Лекции_МО_20.docx
• Тип: Лекции; #359380
• страница: 8 из 9

Вопросы для контроля

1. 
   Что такое уравнения баланса по строкам?
   
2. 
   Что такое уравнения баланса по столбцам?
   
3. 
   Что такое коэффициенты затрат?
   
4. 
   Из каких частей состоит система ограничений транспортной за- дачи?
   
5. 
   Какими особенностями обладает ТЗ?
   
6. 
   Какие ТЗ называются закрытыми, а какие – открытыми?
   
7. 
   Какие клетки в таблицах ТЗ называются базисными, а какие свободными или пустыми?
   
8. 
   Чему должно быть равно число заполненных клеток в базисном допустимом решении?
   
9. 
   Каким условиям должно удовлетворять оптимальное распределе- ние поставок?
   
10. 
    С какой клетки начинается заполнение таблицы при применении метода северо-западного угла?
    
11. 
    С какой клетки начинается заполнение таблицы при применении метода наименьших затрат?
    
12. 
    При исключении строки (столбца), какие клетки перечеркива- ются сплошной линией, а какие клетки пунктирной линией?
    
13. 
    В каком случае дается нулевая поставка?
    
14. 
    Сколько строк (столбцов) можно исключить при заполнении одной клетки?
    
15. 
    Какой из рассмотренных методов приведет быстрее к оптимальному решению?
    

Тема 7. Транспортная задача. Метод потенциалов.(2 часа)

7.1. Критерий оптимальности

базисногораспределенияпоставок.Методпотенциалов.

Транспортная задача – задача на минимум, поэтому оптимум достигнут то- гда и только тогда, когда все коэффициенты при неосновных (свободных) переменных в выражении линейной функции неотрицательны. В Т3произ-

вольная переменная

^xij

отождествляется с содержимым клетки ( i, j). В таб-

лице поставок коэффициент

^ij

при свободной переменной

^xij

в выражении

линейной функции F через свободные переменные, называется оценкой сво-бодной клетки ( i, j ). Тогда критерий оптимальности формулируется следу-ющимобразом:базисноераспределениепоставокоптимальнотогдаитолько тогда, когда оценки всех свободных клеток неотрицательны. Таким образом, в первую очередь следует найти оценки свободных клеток для фик- сированного базисного распределения поставок.

Пусть фиксировано некоторое базисное распределение поставок, при этом

клетка ( i, j)- свободная (переменная

^x_ij- свободная),

_ij- оценка клетки ( i, j),

т.е. коэффициент при переменной рез свободные переменные, т.е.

^xij

в выражении линейной функции Fче-

F F₀  _ijx_ij

 ...,

(1)

^F₀ - суммарные затраты перевозок данного распределения поставок. Тогда из

последнего выражения (1) получим, что оценка _ijсвободной клетки ( i, j)

равна приращению Fсуммарных затрат на перевозку при переводе в клетку

( i, j) единичной поставки (увеличение поставки

^xij

от 0 до 1).

Если

^ij

• 
  0 , то
  

F 0,

а если

_ij 0, то и

F 0 .

Это косвенное определение оценки свободной клетки называется экономиче- ским смыслом свободной клетки. Для нахождения оценок свободных клеток используем экономический смысл указанных оценок.

Вернёмся к примеру из предыдущей лекции.

20

110

40

110

60	1	2 60	5	3
120	1 20	6	5	2 100
100	6	3 50	7 40	4 10

Находим, например оценку свободной клетки (1,3).

Для этого дадим в клетку (1,3) единичную поставку. При этом потребуется изменить поставки в заполненных клетках так, чтобы сохранился баланс по строкам и столбцам. Предположим, что во всех свободных клетках, кроме клетки (1,3), поставки останутся нулевыми.

	20	110	40	110
60	1	2 60	5 1	3
120	1 20	6	5	2 100
100	6	3 50	7 40	4 10

Следует отметить, что найденный вариант перераспределения поставок, за- трагивающий заполненные клетки и увеличивающий поставку клетки (1,3), единственный.

Найдем изменение поставок.

Fсуммарных затрат при указанном перераспределении

Начальные затраты перевозок

F_н:

F_н 2*60 1*20  2*100  3*50  7*40  4*10  340 150  320  810

Затраты после перераспределения:

F_п 2 *59  5*11* 20  2 *100  3*51 7 *39  4 *10  260 123 153  273  809

F F_п F_н

 1

С учетом экономического смысла оценки свободной клетки, следует отметить, что берутся только содержимые измененных клеток:

₁₃  F F_п F_н 2 *(1)  5*1 3*1 7 *(1)  8  9  1

(*)

Так как среди клеток таблицы имеется клетка с отрицательной оцен- кой, то распределение поставок не оптимально.

Предлагается следующий упрошенный способ вычислений.

При вычислении

Fмногие слагаемые

F_пи F_н

взаимно уничтожаются не

влияя на значение F: существенны лишь коэффициенты затрат тех клеток,

в которых постановка при рассматриваемом перераспределении изменится.

При этом в выражении для Fнекоторые входят со знаком «+», а некоторые

со знаком «-». Для нахождения «правильных знаков» удобен чертеж, в кото- ром изображаются клетки, в которых будет заменена поставка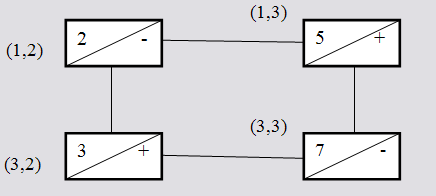

При этом знаком «+» помечены клетки, поставки которых увеличатся, имен-

но их коэффициенты затрат войдут в выражение F со знаком «+». В

остальных клетках поставки уменьшается, они помечены знаком «-» , их ко-

эффициенты затрат входят в выражение Fсо знаком «-».

Ломаная, соединяющая клетки с изменяемой поставной, называется означен- ным циклом пересчета.

Таким образом, можно сформировать первое правило нахождения оценки свободной клетки:

Для свободной клетки следует посмотреть цикл пересчета, в вершинах этого цикла расставить последовательно чередующие знаки, начиная со знака «+» в свободной клетке, тогда значение оценки свободной клетки равно алгебраи- ческой сумме коэффициентов затрат клеток цикла, взятых с соответствую- щими знаками. Означенный цикл пересчета для клетки (1,1) имеет вид: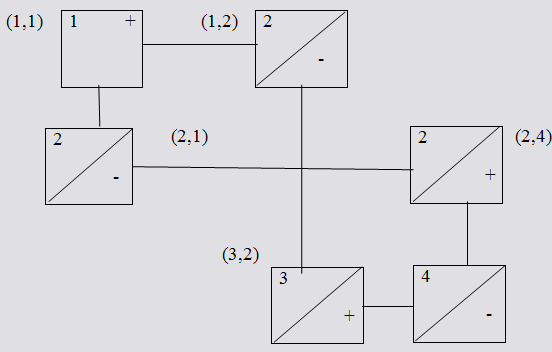



₁₁  (1 2  3)  (2 1 4)  1
Аналогично можно найти оценку любой свободной клетки.

Определение: Циклом в матрице будем называть ломаную с вершинами в клетках со звеньями, лежащими вдоль строк и столбцов матрицы, удовлетво- ряющие условиям:

1. 
   Ломаная должна быть связной, то есть из любой ее вершины можно по- пасть в любую другую вершину по звеньям ломаной;
   
2. 
   В каждой вершине ломаной встречаются два звена, одно из которых рас- полагается по строке, другое – по столбцу.
   

Циклом пересчета называется такой цикл в таблице с базисным распределе- нием поставок, при котором одна из его вершин лежит в свободной клетке, остальные в заполненных. Цикл пересчета называется означенным, если в его вершинах проставлены знаки «+» и «-» так, что в свободной клетке стоит знак «+», а соседние вершины имеют противоположные знаки.

Для каждой свободной клетки базисного распределения поставок существует и притом единственный цикл пересчета.

Мы рассмотрели одно правило нахождения оценок свободных клеток.

Теперь рассмотрим другое правило, существенно упрощающее эту процеду- ру.

Итак, предположим, что коэффициенты затрат всех заполненных клеток рав- ны нулю. Если найти оценки свободных клеток, то окажется, что эти оценки равны к коэффициентам затрат этих же клеток.

Теорема о потенциалах. Оценка свободной клетки не изменится, если к ко- эффициентам затрат некоторой строки (столбца) таблицы прибавить некото- рое одно и то же число. Это число, прибавляемое к коэффициентам затрат выделенной строки (столбца), называется потенциаломданной строки (столбца).

Отсюда получим второе правило определения оценок свободных клеток:

К коэффициентам затрат таблицы поставок в каждой строке и столбценадо прибавить такие числа (потенциалы), чтобы коэффициенты затрат взаполненных клетках стали равными нулю. Полученные при этом коэффици-ентызатратсвободных клетокравныоценкамсвободных клеток.

Рассмотрим предыдущий пример. Пусть требуется найти оценки свободных клеток найденного базисного распределения поставок.

Найдем оценки свободных клеток по второму правилу. Изменение коэффи- циентов затрат можно начинать с любого столбца (строки).

Такая матрица для полученного ранее распределения поставок имеет вид:

^{1 2  5 3} 

 


_1 6 5


6
_ 3  7 

2  _



4  ^

Начнем со второй строки, прибавим к элементам этой строки -1. Далее по порядку: к элементам 4-го столбца прибавим -1; к элементам 3-й строки -3; к элементам 3-го столбца -4; к элементам 1-й строки прибавим -2; и, наконец, к элементам 3-й строки прибавим -3. Все эти операции последовательно по- казаны в следующем виде:

^{1 2  5 3}  ¹

  

^{2  5 3} 



^{1 2  5}



²  ¹

 

2  1

²  ^1

 

0  1

⁰  ^1

 

^{0  1 0} 



_1 6

5 2  _  _ 0  5

4 1 _  _ 0  5 4

0 _  _ 0  5 0

0 _  _ 0  5

0 0  _  _

0  5

0 0  _

6























3



6

6

6

6
^ 3

7  4  ^{ }

3 7 

_{4 } 

3 7 

_3  

3 3

_3 

3 3

3 <sup>

</sup> 0 

0  0  ^

Как видно из последней матрицы, полученное распределение поставок не является оптимальным, так как две оценки свободных клеток отрицательны:

₁₁  1, ₁₃ 1.

Итак, как только будут определены оценки свободных клеток, можно сделать вывод о том, является ли полученное распределение поставок оптимальным.

Вопросы для контроля

1. 
   Расскажите критерий оптимальности распределения поставок.
   
2. 
   Что такое оценка свободной клетки таблицы и чему она равна?
   
3. 
   Какой экономический смысл оценки свободной клетки?
   
4. 
   Расскажите первое правило определения оценки свободной клетки.
   
5. 
   Расскажите второе правило определения оценки свободной клетки.
   
6. 
   Что такое цикл пересчета?
   
7. 
   Какой цикл пересчета называется означенным?
   
8. 
   Что такое потенциал строки (столбца) таблицы поставок?