лекции. Лекции_МО_20. Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)
 Скачать 254.78 Kb. Скачать 254.78 Kb.
|
Тема 4. Симплексные таблицы (2 ч)Применение симплексных таблицНа практике при решении задач линейного программирования удобно ис- пользовать так называемые симплексные таблицы. Пусть решается задачи максимизации. После введения дополнительных переменных систему уравнений и целевую функцию записываем в виде, который называется расширенной системой: a11x1 a12 x2 ... a1nxn b1 a 21x1 a22 x2 ... a2nxn b2 .............................................. a x m1 1 am2 x2 ... amnxn bm F c1 x1 c2 x2 ... cnxn 0 Предполагаем, что все дополнительные переменные имеют тот же знак, что и свободные члены, в противном случае используется M-метод, который рассмотрим позже. Исходную расширенную систему заносим в первую симплексную таблицу. Последняя строка таблицы, в которой приведено уравнение для целевой линейной функции, называется оце- ночной . В ней указываются коэффициенты целевой функции с противопо- ложным знаком fi ci. В левом столбце таблицы записываются основные переменные (ба- зис), в первой строке таблицы – все переменные (отмечая при этом основные), во втором столбце - свободные члены расширенной си- стемы b1,b2 ,...,bm. Последний столбец подготовлен для оценочных отношений, необ- ходимых при расчете наибольшего возможного значения перемен- ной. В рабочую часть таблицы (начиная с третьего столбца и второй строки) занесены коэффициенты aij при переменных. Далее табли- ца преобразуется по определенным правилам. Проверяем выполнение критерия оптимальности при реше- нии задачи максимизации - наличия в последней строке отри- цательных коэффициентов fi 0(ci 0).Если таких нет, то решение оптимально, достигнут max F=C 0 (в левом нижнем углу таблицы), основные переменные принимают значения ai0 (второй столбец - свободные члены), неосновные пере- менные равны 0, то есть получено оптимальное базисное ре- шение. Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент fi 0 в последней  строке определяет разрешающий столбецs. строке определяет разрешающий столбецs.Составим оценочные ограничения по следующим правилам : ∞, если bi и ais имеют разные знаки; ∞, если ∞, если 0, если bi =0, ais = 0 bi=0, ais<0 ais>0 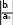 если biи aisимеют одинаковые знаки. если biи aisимеют одинаковые знаки. 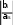 Определяем min Определяем min Если конечного минимума нет, то задача не имеет конечного оптимума и Fmax . Если минимум конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и назначим ее разрешающей строкой,на пере- сечении разрешающей строки и столбца находитсяразрешающийэлементaqs. Переходим к следующей таблице по правилам : А) В левом столбце записываем новый базис: вместо основной переменной xq-переменную xs. Б) В строке функции F, клетках находящихся напротив основных перемен- ных из общего списка переменных, проставляем нули. В) Проставляем единицы – в «своих» клетках (в клетках, находящихся на пересечении каждой основной переменной из столбца основных – базисных переменных с этой же переменной из строки переменных), нули в «чужих» клетках ( в клетках, находящихся на пересечении каждой основной перемен- ной из столбца базисных переменных с другой основной переменной из строки переменных); Г) Новую строку с номером qполучаем из старой, делением на разрешаю- щий элемент aqs. Д) все остальные элементы aijвычисляем по правилу прямоугольника, на одной из вершин которой находится разрешающий элемент, на противопо- ложной по диагонали вершине клетка, для которой в получаемой таблице определяется значение по следующей формуле: ais aqj aij aij a qs a a ij is b b ais bq a a ij i aqs qj qs Далее переходим к пункту III алгоритма. Пример.Решить задачу об использовании ресурсов. рассмотренную ранее, с помощью симплексных таблиц. Решение.Расширенная система задачи имеет вид: x1 3x2 x3 18 2x x x 16 1 2 4 x2 x5 5 3x x 21 1 6 F 2x1 3x2 0 Заполняем первую симплексную таблицу, в которой переменные. Смотрим пункт II алгоритма. x3 , x4 , x5 , x6 основные Таблица №1
  В соответствии с п. III алгоритма, проверяем критерий оптимальности (нали- чие отрицательных коэффициентов в последней строке таблицы). В послед- ней строке таблицы имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю (-3), поэтому второй столбец разрешающий: пе- ременная х2переходит в основные. В соответствии с п. IV находим оценоч- В соответствии с п. III алгоритма, проверяем критерий оптимальности (нали- чие отрицательных коэффициентов в последней строке таблицы). В послед- ней строке таблицы имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю (-3), поэтому второй столбец разрешающий: пе- ременная х2переходит в основные. В соответствии с п. IV находим оценоч-ное отношение и х2= Третья строка является разрешающей (отмечена горизонтальной стрелкой). На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент а32=1. Строим таблицу 2 в соответствии с п. V алгоритма: А) Новое деление переменных: основные переменные x3, x4,x2,x6; неоснов- ные x1,x5. Б) В последней строке, в клетки находящиеся напротив основных перемен- ных x3,x4,x2,x6, вставляем нули. В) Каждый элемент 3-й строки (разрешающей строки) делится на разрешаю- щий элемент и пишутся в эту строку новой таблицы ( табл.№2). Г).Все остальные элементы находим по правилу прямоугольников: b'1 18 5 3 3, 1 ' 16 5 1 11, b 2 1 ' 21 5 0 21. b 4 1 a' 1 0 1 1, a' 2 0 1 2, a' 3 0 0 3, f' 2 (3) 0 2. 1 1 2 1 4 1 1 1 F 0 (3) 5 15. 1 1 Таким образом, получим следующую таблицу, соответствующую второму базисному допустимому решению: Таблица №2
↑ Критерий оптимальности не выполнен, так как в последней строке имеется отрицательный элемент, поэтому 1-й столбец разрешающий; основные. x1 min{3;5;5;7} 3, x1 переходит в Это достигается в первой строке, поэтому 1-я строка разрешающая – х3пе- реходит в неосновные. Продолжая аналогичным путем, в соответствии с алгоритмом, получим ис- комое решение. М-метод (Метод искусственного базиса) Ранее рассмотрели алгоритм получения допустимого базисного решения в случае, когда первоначальное базисное решение недопустимо. Но при при- менении симплексных таблиц, в подобной ситуации удобнее пользоваться так называемым М-методом, или методом искусственного базиса. В каждое уравнение, дающее отрицательную компоненту в базисном реше- нии, вводим свою новую неотрицательную искусственную переменную y1, y2 ,..., yк , которое имеет тот же знак, что и свободный член в правой части уравнения. В первой таблице, включаем в число основных все искусственные переменные и те обычные дополнительные переменные, которые определя- ют неотрицательные компоненты базисного решения. Составляем новую линейную функцию. T F M( y1 y2 ... yк), где М - произвольное большое число, и ищем максимум функции Т. Это называется еще Т- задачей. Выражение функцией. Имеет место следующая теорема: M( y1 y2 ... yk) называется М – Если в оптимальном решении Т – задачи все искусственные пере- менные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи, т.е. т.е. min M – функции равен 0. Tmax Fmax , если y1 y2 ... yR 0. Если имеется оптимальное решение Т – задачи, в котором хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи не совместна. Если Tmax , то исходная задача также неразрешима, причем либо Fmax , либо условия значения противоречивы. Из теоремы следует, что вначале следует найти минимум М- функ- ции. Если он равен нулю, то и все искусственные переменные обращаются в ноль, то можно отбросить эти переменные и решать исходную задачу, находя из полученного базисного решения. На практике находят не минимум М- функции, а максимум (-М)- функции. Пример: Пусть решается задача F x1 2x2 max при ограничениях x1 x2 1 x x 3 1 2 x 3 1 x1 , x2 0 x1 x2 x3 1 x x x 3 1 2 4 x x 3 1 5 X1 (0;0;1;3;3) - недопустимое базисное решение В 1-е уравнение введем переменную у1, с тем же знаком, что и сво- бодный член: x x x y 1 x1 x2 x3 y 1 1 2 3 1 x x x 3 x x x 3 или 1 2 4 1 2 4 x x 3 x x 3 1 5 1 5 F x1 2x2 0 T x1 2x2 My1 max
Последняя строка (-М) функция равна (- (Mф) y1 Последняя строка это (-М) функция, т.е Mф y1 . Заполняем ее, умножая строку y1 на (-М). Проверяем выполнение критерия оптимальности при максимизации (-М) функции. В строке для –Mфимеется отрицательный элемент во вто- ром столбце, он и разрешающий , переменная x2 переходит в основные. Находим оценочное отношение: минимальное отношение находятся в первой строке, она и разрешающая. Разрешающий элемент a12 1, переменная y1 пе- реходит в неосновные, обращается в ноль на следующем базисном решении далее исключается из рассмотрения. В соответствии с общим алгоритмом получим следующую таблицу:
Последняя строка показывает, что критерий оптимальности при мак- симизации - Mф выполнен: max (- Mф)=0, значит min Mф=0, далее эту строку не рассматриваем. Получено допустимое базисное решение X1 (0;1;0;2;3) . Начиная с этого решаем задачу по обычному алгоритму. Критерий оп- тимальности для F не выполнен, имеются два отрицательных элемента; Возьмем столбец, в котором коэффициент при х1отрицательный: -3 он и разрешающий, следовательно x1 переходит в основные. Строка, в которой минимальная оценка (3) – разрешающая, разрешающий элемент a32 1 Как видно, переменная x5 переходит в неосновные. Получим следующую таблицу:
x3 - в основные, x4 - в неосновные. a23 1.
Т.о. получили оптимальное решение: Fmax=15; X=(3;5; 2;0; 0). Вопросы для контроля Как составляется расширенная система ограничений? Каким образом заполняем первую симплексную таблицу? Как проверяется критерий оптимальности решения? Какой столбец называется разрешающим столбцом? Какая строка является разрешающей? Что такое «свои» и «чужие» клетки? Расскажите о правиле прямоугольников при заполнении некото- рых клеток новой симплексной таблицы. В каких случаях используется М – метод? Для чего применяются искусственные переменные? 10.Что такое Т – задача? Как составляется М – функция? При каких значениях искусственных переменных, Т – задача имеет оптимальное решение? В каком случае система ограничений задачи является несовмест- ной? Когда исходная задача является неразрешимой? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
