лекции. Лекции_МО_20. Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)

• Название: Лекции по методам оптимизации Тема Общая постановка задачи линейного программирования (2часа)
• Анкор: лекции
• Дата: 12.02.2022
• Размер: 254.78 Kb.
• Имя файла: Лекции_МО_20.docx
• Тип: Лекции; #359380
• страница: 4 из 9

Если в выражении линейной функции через неосновные переменные от- сутствуют положительные коэффициенты при неосновных перемен- ных, то решение оптимально.

2. 
   Алгоритмвходавдопустимуюобласть
   

Получение первоначального допустимого базисного решения яв- ляется важным моментом в решении задачи линейного программирова- ния и тем самым осуществляется вход в допустимую область. Как толь- ко находится первое базисное допустимое решение, дальше симплекс- ный метод не позволит выйти из допустимой области решений и по кратчайшему пути приводит к оптимальному решению.

Общий алгоритм получения первоначального допустимого базового реше- ния:

1. 
   Если каждая дополнительная переменная входит в уравнение с тем же знаком, что и свободный член, стоящий в правой части уравнения, то дополнительные переменные можно взять в качестве основных на I шаге. При этом получится допустимое базисное решение.
   
2. 
   Если первое базисное решение получилось недопустимым, например, в качестве основных взяты дополнительные переменные, но хотя бы од- на из них входила в уравнение со знаком, противоположным знаку сво- бодного члена, то рассмотрим уравнение, содержащее отрицательный свободный член (любое, если их несколько), и переводим в основные ту неосновную переменную, которая входит в это уравнение с положи- тельным коэффициентом (любую, если их несколько).
   

Такие шаги повторяются до тех пор, пока не достигается допустимое базисное решение.

3. 
   Если базисное решение недопустимое, а в уравнении, содержащем от- рицательный свободный член, отсутствует неосновная переменная с положительным коэффициентом, то в этом случае допустимое базис- ное решение получить невозможно, т.е. задача не имеет решения.
   

2-я задача.

F 2x₁  3x₂  max

<sup>2x1  3x2  12

</sup> x x 7

_ 1 2

_2x₁  x₂  10


x

 2


_ 2

_^ x₁  0

Введем дополнительные переменные:

<sup>2x1  3x2  x3  12

</sup> x x x 7

^ 1 2

^2x x x

4

 10

(7)

_ 1 2 5

_^ x₂  x₆  2

Возьмем в начале в качестве основных переменных дополнительные переменные, так как они удовлетворяют известному требованию.

I-шаг. Основные переменные: x₃ , x₄ , x₅ , x₆ .

Неосновные переменные: x₁ , x₂ .

Выразим основные через неосновные:



^{x3  12  2x1  3x2}

x


_{ 4}  7  x₁  x₂
(8)

x
_{ 5}  10  2x₁  x₂

^_x₆  2  x₂

x₁  (0;0;12;7;10;2) 

значения.
недопустимые т.к. имеются два отрицательных

Для получения первоначального допустимого базисного решения, со- гласно вышеуказанному алгоритму, поступаем следующим образом: Выбираем любое уравнение, содержащее отрицательный свободный член, например, первое и в нем – любую неосновную переменную с

положительным коэффициентом и переведем в основные:

^x1 или

x_{2 ,}

пусть возьмем

^x₁ . Наиболее возможное значение

2




x min^12 ; ; ¹⁰ ; ^  5

1 ^ ₂ ^

Это достигается в 3-м уравнении; оно же разрешающее и переменная

x₅ переходит в неосновные.

II шаг. Основные переменные;

x₁ , x₃ , x₄ , x₆ ;

Неосновные;

x₂ , x₅ .

^x 5  ¹ x ¹ x

_ 1 ₂ 2 ₂ 5

x

 3

2
^  12  10  x x

5

 3x₂

 2  2x₂

• 
  x₅
  

1



3
^x 12 


3


₂ x₂ 

₂ x₅  x₂  12 

₂ x₂ 

1

₂ x₅

x

1

 6

2
^  2  x

При этом не исчезли отрицательные свободные члены, т.е. базисное

решение также недопустимое. Поэтому не следует переводить x₁ в ос-

новные. Отсюда следует, что в основные надо переводить

x₂ , тогда

наибольшее возможное значение

x₂ :

x min^12 ; 7;10; 2 ^  2.

2 ^{ }


3
 

Это достигается в четвертом уравнении, оно и разрешающее, поэтому

x₆ переходит в неосновные.

II шаг. Основные переменные:

x₂ , x₃ , x₄ , x₅ .

Неосновные переменные: x₁ , x₆ .

Выражаем новые основные переменные через новые неосновные:

^x2

_x

 2  x₆

 6  2x

• 
  3x
  


^ 3 1 6


x
_{ 4}  5  x₁  x₆

^_x₅  8  2x₁  x₆

x₂  (0;2;6;5;8;0) - недопустимое базисное решение с одной отрицатель- ной компонентой. Возьмем 2-е уравнение с отрицательным свободным членом и переведем в основные одну из неосновных переменных,

^x₁ или ^x_6, входящих в уравнение с положительным коэффициентом.

Получим из уравнения их наибольшее возможное значение:

x₂ min;3;;4 3

достигается во 2-м уравнении.

x₆ min ;2;5;8  2

достигается также во 2-м уравнении, т.е. в обоих случаях второе урав-

нение разрешающее. В данной ситуации можно выбрать любую из

x₆ , чтобы перевести в основные.

x₁ и

Переведем

x₆ в основные, то

x₃ переходит в неосновные.

III-шаг. Основные: x₂ , x₄ , x₅ , x₆ .

Неосновные: x₁, x₃ .


3

3
^x 2  ² x ¹ x

_ 6 1 3



^x 4  ² x ¹ x

_ 2



^x 3 

₃ 1 ₃ 3

⁵ x ¹ x

_ 4 ₃ 1 ₃ 3

^ 4 1

^x₅  6 



₃ x₁ 

₃ x₃

x₃  (0; 4;0;3;6; 2) - допустимое базисное решение.

3. 
   Минимизациялинейнойфункции
   

При определении минимума функции Z возможны два способа:

1. 
   Отыскать максимум функции F, полагая F=-Z и учитывая, что = -F _max ;
   
2. 
   Модифицировать симплексный метод: На каждом шаге уменьшать мини- мальную функцию за счет той неосновной переменной, которая входит в вы- ражение минимальной функции с отрицательным коэффициентом.
   

Пример.

Z= 18y₁ +16y ₂ +5y ₃ +21y ₄  min

при

 ^{y1  2 y2  3y4  2}



_3y₁  y₂  y₃  3, y_i 0, i 1,2,3,4

Введем дополнительные неотрицательные переменные y ₅ ,y ₆ со знаком ми- нус, так как в ограничениях неравенства имеют вид «≥»:



 ^{y1  2 y2  3y4  y5  2}

_3y₁  y₂  y₃  y₆  3

1. 
   
   .
   Основные y,y; неосновные y ,y ,y ,y
   

_{5 6} 1 2 ₃ 4


 ^{y5  2  y1  2 y2  3y4}


y
_{ 6}  3  3y₁  y₂  y₃

Y=(0;0;0;0;-2;-3) – недопустимое базисное решение.

0
В данной ситуации, в начале, в качестве основных, удобно взять перемен- ные y ₃ и y ₄ (согласно первому ,коэффициенты при y ₃ и y ₄ положительны).

 шаг. Основные y ₃ ,y ₄ ; неосновные y₁ ,y ₂ ,y ₅ ,y _{6 .}



 ^{y3  3  3y1  y2  y6}

^ y ²  ¹ y

• 
  ² y
  

• 
  ¹ y
  

_ ⁴

3 3 ¹

₃ 2 ₃ 5
_ 2

Получим Y₁

(0;0;3; ;0;0)

3 _.

Выразим функцию Z через неосновные переменные:

Z 18y 16 y 5(3  3y y y)  21( ²  ¹ y

 ² y ¹ y) 



1 2 1 2 6

3 3 ¹ 3 ² 3 ⁵

18y₁  16 y₂  15 15y₁  5y₂  5 y₆  14  7 y₁ 14 y₂  29  4 y₁  3y₂  7 y₅  5y₆
Z₁  Z(Y₁)  29 не является минимальным, так как значение Z можно

уменьшить за счет перевода в основные

^y₁ или

^y_{2 ,} имеющих в выражении

для Z отрицательные коэффициенты. Возьмем коэффициентом и переведем ее в основные.

^y₁ с наибольшим по модулю

Для нее определим наибольшее возможное значение :

y₃  3  3y₁  0

y₁  1

y ²  ¹ y 0

4 _{3 3} 1

y₁  2

y₁  min1; 2 1соответствует 1-му уравнению, оно и является разреша-

ющим, y₃ - переходит в неосновные . Изменение целевой функции:

₁  4 1  4

2. 
   шаг. Основные
   

y_1, y_{4 ,} неосновные
^y2, ^y3, ^y5, ^y6 _.

^ y 1  ¹ y ¹ y ¹ y

_ 1 ₃ 2 ₃ 3 ₃ 6

^ 1 5 1 1 1

y


_ 3

  (

3 9

) y₂

 ₉ y₃

 ₃ y₅

 ₉ y₆

Y₂ 

1

(1;0;0; ;0;0)

3

-допустимое и

Z 25  ⁵ y

₃ 2

• 
  ⁴ y
  

₃ 3

 7 y<sub>5

</sub> 11 <sub>y

3</sub> 6

Z₂  25; Z₂  Z₁  25  29  4
 можно уменьшить за счет перевода в основные переменную ^y₂ ,то

наибольшее возможное значение

x_{2 :}

2
 ^{y 3}







y min_3;

³ _


³ соответствует 2-му уравнению, оно раз-

^ _y ¹ _ ⁹ _ ³ 2



5^ 5

_ ²

3 5 5 ^{ }

решающее, y₄ -переходит в неосновные. Изменение целевой функции:

 ₂

 ³ (⁵)

5 3

 1;

2. 
   шаг. Основные
   

y₁ ; y₂ ;

неосновные

^y3, ^y4, ^y5, ^y6

^ y ¹  ⁹  ¹  ⁹ y ⁹ y


 ¹  ⁹ y


 ¹  ⁹ y

3

5

9

5

5
_ 2 3 4



3 5 ⁵

9 5 ⁶

^ ³  ¹ y ⁹ y ³ y ¹ y

^ 3 4 5 6


5

5

5
_ 5 2

^ y ⁴  ² y ³ y ¹ y ² y

_ 1 _{5 5} 3 ₅ 4 ₅ 5 ₅ 6

_Y 4 3

₃ ( ₅

; ;0;0;0;0)

5

Выражаем целевую функцию через неосновные переменные:

Z y₃  3y₄  6y₅  4y₄

Так как, в полученном выражении отсутствуют переменные с отрица- тельным коэффициентом, это решение является оптимальным.

Y₃ 

( ⁴ ;

5

³ ;0;0;0;0)

5

оптимальное решение,

^min

 Z₀

 Z(₃ )  24;

Критерийоптимальностиприминимизациилинейнойфункции:

Если в выражении линейной функции через неосновные переменныеотсутствуют отрицательные коэффициенты при неосновных переменных,то решениеоптимально.

Замечание.На каждом шаге симплексного метода какая-либо неоснов- ная переменная переводится в основные, при этом каждое уравнение системы ограничений определяет конечное или бесконечное наиболь- шее возможное значение этой переменной - оценочное отношение. При этом могут встречаться различные случаи оценки роста неосновной переменной, которые зависят от знаков и значений свободного члена и коэффициента при переводимой переменной. Рассмотрим все возмож- ные случаи.

Введем обозначения:
x_i-переводимая неосновная переменная;

b_j-свободный член;

a_ij-коэффициент при
x_i.

В общем виде уравнение имеет вид:
x_j b_j  ...  a_ijx_i ... ( x_j-основная переменная)

Наибольшее возможное значение вилам:

^x_iопределяется по следующим пра-

1. 
   x
   

если

b и a разного знака и

^a≠0 , b≠0;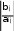

ⁱ j ij

ij _j

2. 
   ^x_j=∞, если b_j
   

^{и a}ij

одного знака и

^a_ij≠0, b_j≠0;

3. 
   x_j 0
   

, если b_j=0 и

a_ij<0;

4. 
   ^x_i=∞, если
   

5. 
   ^x_i=∞, если
   

^b_j=0 и
^a_ij=0.

a_ij> 0;

Особыеслучаисимплексногометода.

1. 
   Неединственностьоптимальногорешения.
   

Пример .

При ограничениях:

F 3x₁  3x₂  max

^{x1  x2  8}

^2x x 1

^ 1 2

^x 2x
 2, x,  0, x 0

 1 2 2

На очередном шаге получаем:

Основные переменные:

x₁ , x₂ , x₅ ; Неосновные переменные:

x₃ , x₄ .

Выражение основных переменных через неосновные имеет вид:

3

3
^x 5  ² x ¹ x

_ 1 3 4



x

^ 2
^  3  ¹ x

_{ 3} 3

• 
  ¹ x
  

₃ 4

^x₅ ^{ 9  x}₃ ^{ x}₄

_

x₁  (5;3;0;0;9)- допустимое базисное решение. Линейная функция

F=24- x₃. В этом выражении отсутствует неосновные переменные с положи- тельным коэффициентом, критерий оптимальности выполнен, следовательно

^x1 оптимальное базисное решение, F_max  F( X₁ )  24.
Однако в последнем выражении Fотсутствует неосновная переменная x₄
или формально входит с нулевым коэффициентом, поэтому изменение этой переменной не приведет к изменению значения функции F. Например, можно перевести в основные переменную x₄ :

x₄ =min {15;∞;9}=9;

При этом переменная

^x_sпереходит в неосновные, но изменение линейной

функции F не произойдет:

∆F=9*0=0;

Действительно на следующем шаге получим новое базисное решение

x₂ =(6;2;0;9;0). Учитывая, что переменная x₃ =0 (неосновная), а переменная x₄

удовлетворяет неравенству 0≤ x₄ ≤9, из системы уравнений можно получить все множество оптимальных решений задачи.

Для удобства введем обозначение

ных решений:

^x4 =t, t[0;9], тогда множество оптималь-

x 3  ¹ t,

1 ₃
x 5  ¹ t,

2 ₃

x₃  0,

x₄  t,

x₅  9  t,
t[0;9].

Замечание.Множество оптимальных решений можно представить как вы- пуклую линейную комбинацию Xбазисных решений, например:

X₁  (3;5;0;0;9) и

X₂ (6;2;0;9;0),

т.е.

X X_1  (1 ) X₂ , где 0≤ ≤1

2. 
   Появлениевырожденногобазисногорешения.
   

Иногда при решении симплексным методом (СМ) можно получить вырож- денное базисное решение (нулевое значение основной переменной).

В этом случае в следующем шагу симплексного метода значение F не улуч- шится. Наличие таких «пустых» шагов может привести и так называемому

«зацикливанию». В связи с этим можно сделать вывод:

Если на каком-либо шаге наибольшее возможное значение переменной до- стигается в нескольких уравнениях одновременно, то разрешающим является любое из них. На следующем шаге получаем вырожденное базисное реше- ние, переход к очередному базисному решению может не изменить функцию цели (∆F=0).

3. 
   Отсутствиеконечногооптимума.
   

При отсутствии конечного оптимума получим

F_min =-∞ при минимизации.

F_max =∞ при максимизации и

Примечание. Если на каком-либо шаге получаем, что во всех уравнениях си- стемы ограничений бесконечны оценочные отношения той переменной, ко- торая переводится в основные, то задача не имеет конечного оптимума.

Вывод.Если система ограничений непротиворечива, то выполнение конеч- ного числа шагов симплексного метода либо приводит к получению опти- мального решения, либо к установлению того факта, что целевая функция не имеет конечного оптимума.

Вопросы для контроля

1. 
   Что такое разрешающее уравнение?
   
2. 
   Как находится переменная, которую следует перевести в основные?
   
3. 
   Как находится переменная, которую следует перевести в неосновные?
   
4. 
   Расскажите критерий оптимальности при максимизации линейной функции?
   
5. 
   Как находится первоначальное допустимое базисное решение?
   
6. 
   Расскажите алгоритм симплексного метода при максимизации линей- ной функции.
   
7. 
   Расскажите критерий оптимальности максимизации линейной функ- ции.
   
8. 
   Как выразить целевую функцию через очередные неосновные пере- менные?
   
9. 
   Как следует поступить, если первоначальное базисное решение окажет- ся недопустимым?
   
10. 
    Чем отличается симплексный метод при минимизации функции от максимизации функции?
    
11. 
    Расскажите критерий оптимальности при минимизации линейной функции симплексным методом.
    
12. 
    Когда оптимальное решение задачи ЛП не является оптимальным? 13.В какой ситуации не улучшится значение целевой линейной функ-
    

ции?

14. 
    В какой ситуации отсутствует конечный оптимум?