Лекции. Лекции ТММ. Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика

• Название: Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика
• Анкор: Лекции
• Дата: 16.01.2023
• Размер: 5.61 Mb.
• Имя файла: Лекции ТММ.doc
• Тип: Лекции; #888798
• страница: 7 из 9

основные понятия динамики механизмов.

Задачи динамического исследования.
6.1. Силы и их механические характеристики. Работа и мощность. Классификация сил по знаку работы и мощности. ([1], §40; [2], §4.1)

6.2. Динамическая модель механизма (машины). ([2], §4.2)

6.3. Приведение сил. ([1], §67-69; [2], §4.3)

6.4. Приведение масс. ([1], §70-71; [2], §4.4)

5. 
   Уравнение движения машины. ([1], §72; [2], §4.5)
   
6. 
   Задачи динамического исследования механизмов. ([1], §38; [2], §3.3)
   

1. 
   Силы и их механические характеристики. Работа и мощность. Классификация сил по знаку работы и мощности.
   

Работа и мощность – это механические характеристики результативности действия приложенной к телу силы или момента пары сил.
Работа силы (момента пары сил) – это скалярная величина, характеризующая действие силы (момента пары сил), приложенной к телу, на некотором его перемещении.

Элементарная работа силы равна произведению проекции , касательной к траектории точки приложения силы, на модуль элементарного перемещения точки, т.е.:

(6.1)

При этом, направление касательной оси должно совпадать с направлением вектора скорости точки приложения силы. Если > 0 – элементарная работа положительна. Если < 0 – элементарная работа отрицательна. Если = 0 – работа равна нулю.
Элементарная работа момента пары сил равна произведению величины момента на элементарный угол поворота тела, к которому приложен момент, т.е.:

(6.2)

Знак «+» ставится, если направление момента и направление угловой скорости тела, к которому приложен момент, совпадают; знак «–» - если они противоположны.
Работа силы или момента на произвольном перемещении равна интегральной сумме соответствующих элементарных работ:

(6.3)

За единицу работы в системе СИ принят джоуль (1 Дж = 1 Н·м).

Мощностью силы (момента пары сил) называют величину, которая показывает работу, выполненную силой (моментом) за единицу времени.

Если работа совершается равномерно, то мощность находят по формуле:

, (6.4)

где - время, в течение которого произведена работа.

В общем случае:

(6.5)
(6.6)
Мощность силы [см. (6.5)] равна произведению касательной составляющей силы на величину скорости точки, в которой приложена сила. Направление касательной оси , при этом, должно совпадать с направлением вектора скорости точки. Если > 0 – мощность силы положительная. Если < 0 – мощность отрицательная. Если = 0 – мощность равна нулю.
Мощность момента пары сил [см. (6.6)] равна произведению величины момента на модуль угловой скорости тела, к которому приложен момент. В (6.6) знак «+» ставится, если направление момента и направление угловой скорости тела, к которому приложен момент, совпадают; знак «–» - если они противоположны.
Единицей измерения мощности в СИ является ватт (1 Вт = 1 Дж/с). В технике за единицу мощности часто принимают лошадиную силу (1 л.с. = 736 Вт).

Из (6.4) следует, что при постоянной мощности работу, произведенную машиной, можно измерять произведением ее мощности на время работы. Отсюда возникла часто употребляемая в технике единица измерения работы киловатт-час (1 кВт·ч = 3,6 · 10⁶ Дж).
Из равенства видно, что у двигателя, имеющего некоторую мощность , сила тяги будет тем больше, чем меньше скорость . Поэтому среднюю скорость выходного звена механизма на рабочем ходу намеренно снижают, а на холостом ходу – увеличивают. Об этом уже упоминалось ранее (см. Лекция 3, п.3.6, сноска 1).
Итак, работа и мощность сил могут быть положительными, отрицательными и равными нулю. По этому признаку все силы, действующие на механизм, могут быть классифицированы на движущие, силы сопротивления и безразличные (Рис.6.1).

Движущие силы – силы, направленные в сторону движения механизма и стремящиеся ускорить это движение. Выполняют положительную работу (А  0) и имеют положительную мощность (  0).
Силы сопротивления – силы, направленные против движения механизма и стремящиеся затормозить это движение. Выполняют отрицательную работу (А0) и имеют отрицательную мощность (  0).
Безразличные силы – силы, действие которых не ускоряет и не замедляет движение механизма (А = 0, N= 0).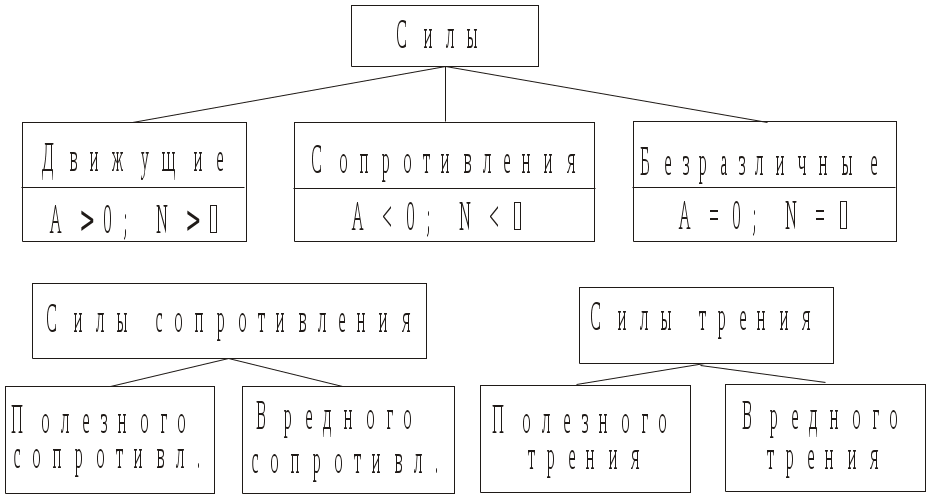





Рис.6.1
Из рис.6.1 видно, что силы сопротивления также классифицируются.
Силы полезного сопротивления – силы, для преодоления которых механизм создавался (имеется в виду выполняемая механизмом “полезная” работа или технологическое задание, а именно: снятие стружки при обработке детали станком, деформация металла в прокатной клети, перемещение грунта бульдозером, подъём груза и т.д.).

Силы вредного сопротивления – силы сопротивления движению, возникающие попутно с полезными; не связанные с выполнением технологического задания, создающие дополнительные трудности для механизма и уменьшающие КПД механизма (трение в кинематических парах, сопротивление воздуха, гидродинамическое трение в гидравлических механизмах и т.д.).
Деление сил на движущие и силы сопротивления является условным. Так, например: силы тяжести звеньев при подъеме точек их приложения совершают отрицательную работу (А  0), т.е. являются силами сопротивления, а при опускании - движущими (А  0), т. е. помогают движению механизма. Эта же сила при перемещении её точки приложения по горизонтали является безразличной (А = 0).

Аналогично можно показать различное влияние сил упругости пружин, являющихся внешними для механизма силами (А  0, А  0 при различных фазах работы механизма).
По аналогии с силами сопротивления, силы трения в механизмах также можно разделить на силы вредного трения и силы полезного трения (Рис.6.1).

Примером вредного трения может служить трение в подшипниках. Это трение стремятся уменьшить, совершенствуя конструкцию подшипника: подшипник скольжения  подшипник качения  подшипник жидкостного трения (ПЖТ).

Примерами полезного трения являются трение в ременной, фрикционной передачах, в передачах винт-гайка и др. Здесь явление трения является полезным, так как определяет работоспособность механизма. В этих случаях силу трения, наоборот, стремятся увеличить. Так, увеличенная сила трения между ремнем и шкивом в клиноременной передаче улучшает ее показатели, по сравнению с плоскоременной. В нажимных винтах прокатных станов или винтовых домкратах трение увеличивают за счет уменьшения угла наклона резьбы, не допуская тем самым самопроизвольного отвинчивания винта.
При динамическом синтезе и анализе механизмов силы и моменты сил считают известными. Они могут задаваться графически (т.е. графиком, рис.6.2) или аналитически (математической формулой).



Рис.6.2

2. 
   Динамическая модель механизма (машины).
   

В большинстве случаев механизмы и состоящие из них машины представляют собой сложные многозвенные системы. Движущие силы и моменты сил, а также силы и моменты сил сопротивления приложены к различным звеньям, образуя сложную картину нагружения механизма. Определение закона движения таких систем – довольно трудная задача.
В ТММ разработан и успешно используется во всех специальных дисциплинах метод решения задач динамики, при котором сам механизм (или машина) заменяется так называемой «динамической моделью». В качестве динамической модели обычно используют простой механизм, состоящий из стойки и одного подвижного звена.
Замена преследует две цели:

1. 
   Максимально упростить заменяемый механизм с точки зрения его структуры.
   
2. 
   Сохранить динамическую эквивалентность заменяемого и заменяющего механизмов. Это означает, что движение начального звена исходного механизма и его динамического аналога - начального звена динамической модели должно быть строго одинаковым (тождественным).
   

Рассмотрим цепочку рассуждений, приводящих к идее построения динамической модели, на примере шестизвенного механизма качающегося конвейера (Рис.6.3).


Представленный на рис.6.3,а механизм имеет W=1. Это значит, что существует один независимый параметр, однозначно определяющий положение всех звеньев механизма в любой момент времени. Этот параметр называют обобщенной координатой. В качестве обобщенной координаты, в данном случае, удобно принять функцию положения ведущего звена (угол поворота кривошипа ОА). В этом случае кривошип становится уже начальным звеном. Если движение начального звена определяет движение всего механизма, значит, именно начальное звено и его закон движения становятся главной целью исследования. Отсюда логически вытекает желание заменить сложный многозвенный механизм простым двухзвенным механизмом (Рис.6.3,б), в котором начальное звено полностью повторяет движение начального звена исходного механизма. Если это удается реализовать, получают «динамическую модель» механизма.
Но как заставить начальное звено динамической модели двигаться по закону движения начального звена исходного механизма?
Чтобы выяснить это, т.е. определить условия, необходимые для одинакового движения двух вращающихся звеньев (кривошипа ОА в механизме и звена ОА в динамической модели) рассмотрим их уравнения движения.
Уравнение движения исходного механизма можно записать в форме уравнения кинетической энергии:
, (6.7)
где и - кинетическая энергия механизма в начале и в конце конечного промежутка времени , в течение которого обобщенная координата изменяется на величину ;

и - работы движущих сил и сил сопротивления, действующих на звенья механизма, в промежуток времени .
Если за звено приведения данного механизма принять кривошип ОА, то можно получить уравнение движения звена приведения в виде: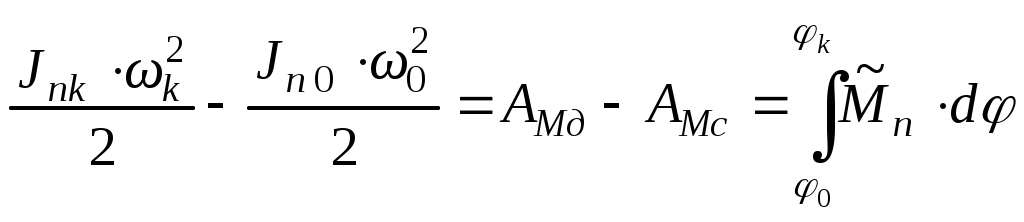
, (6.8)
где и - приведенный к звену приведения момент инерции звеньев механизма в конце и в начале промежутка времени ;

и - угловая скорость звена приведения в конце и в начале промежутка времени ;

и - работа приведенных к звену приведения моментов движущих сил и сил сопротивления за промежуток времени ;

- приведенный к звену приведения момент движущих сил (+) и сил сопротивления (-) в момент времени из интервала , когда обобщенная координата принимает значение из интервала .

С другой стороны, движение начального звена динамической модели (звено совершает вращательное движение) можно описать уравнением: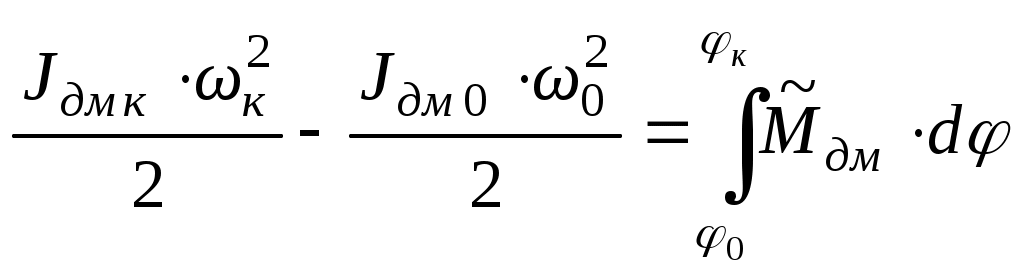
, (6.9)

где и - момент инерции начального звена динамической модели в моменты и соответственно;

и - угловая скорость начального звена динамической модели в моменты и ;

и - конечное и начальное значения обобщенной координаты ;

- момент сил, приложенный к начальному звену динамической модели, в мгновение, когда из интервала .
Сопоставляя уравнения движения (6.8) и (6.9), можно прийти к следующему выводу.
Движение начальных звеньев многозвенного механизма и динамической модели (Рис.6.3) будет тождественным, если в любой момент времени выполняются условия:

1. 
   Момент инерции начального звена динамической модели равен приведенному к кривошипу ОА моменту инерции звеньев основного механизма .
   
2. 
   Момент сил, приложенных к начальному звену динамической модели , равен приведенному к кривошипу ОА моменту сил, действующих на звенья основного механизма.
   

Выполнение этих 2-х условий гарантирует полное соответствие законов движения начального звена динамической модели и начального звена исходного механизма. Обобщенные координаты механизмов, в этом случае, в каждый момент времени будут тождественными, т.е. совпадающими по направлению и величине.
Другими словами, для полной тождественности кинематических характеристик начальных звеньев исходный механизм и его динамическая модель должны иметь совпадающие в любой момент времени силовые и инерционные характеристики. Эти силовые и инерционные характеристики могут быть найдены по правилам приведения сил и масс, которые рассмотрены ниже.
В заключении раздела следует подчеркнуть, что созданная динамическая модель является объектом воображаемым, придуманным исключительно для удобства решения задач динамики механизмов.

3. 
   Приведение сил.
   

Итак, для определения силовой характеристики динамической модели необходимо вычислить приведенную к начальному звену многозвенного механизма силу или приведенный момент сил. Если находят приведенную силу, то ее направление (для удобства вычислений) удобно принять по перпендикуляру к звену ОА.

В основу уравнений для определения приведенной силы (момента сил) положены критерии, обозначенные в следующих определениях.
Приведенная сила – это виртуальная сила, приложенная к точке приведения звена приведения механизма, работа или мощность которой равна суммарной работе или мощности всех активных и реактивных сил и моментов, действующих на звенья механизма.
Приведенный момент – это виртуальный (воображаемый) момент, приложенный к звену приведения, работа или мощность которого равна суммарной работе или мощности всех активных и реактивных сил и моментов, действующих на звенья механизма.
Как видно из определений, приведенная сила вычисляется из условия равенства работ приведенной (заменяющей) силы и всех заменяемых ею сил на любом возможном перемещении системы. Учитывая, что возможные перемещения точек приложения сил пропорциональны возможным скоростям, условие равенства работ может быть заменено условием равенства соответствующих мощностей.
Таким образом, для механизма с звеньями можно записать:
(6.10)
где (6.11)
или (6.12)
Отсюда величина приведенной силы:
(6.13)
или приведенный момент:
(6.14)
Для закрепления материала рассмотрим пример определения приведенной силы в механизме, показанном на рис.6.4.

Пример 1.
О 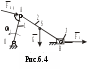пределить приведенную силу сопротивления и веса для данного (Рис.6.4) положения механизма. Приведенная сила должна заменять суммарное действие силы веса и силы сопротивления . За точку приведения взять точку А конца кривошипа. Направление силы принять перпендикулярно ОА.

Решение

1. 
   Изображаем механизм в заданном положении. Изображаем силы, действующие на него, приложив их в соответствующих точках. В точке приве дения (точке А) прикладываем искомую приведенную силу, направив ее перпендикулярно ОА в произвольном направлении (например, против угловой скорости кривошипа).
   
2. 
   При определении приведенной силы должно выполняться : .
   
3. 
   Задавшись скоростью движения кривошипа, определим скорости точек и , после чего составим уравнение мощностей:
   

(6.15)
При определении мощностей сил формулу

можно заменить:

- произведением скорости точки на величину проекции силы на направление скорости (с учетом знака проекции), т.е. ;

- произведением силы на величину проекции скорости на направление силы (с учетом знака проекции), т.е. .

В (6.15) использован второй из вариантов.

4. 
   Из (6.15) следует: (6.16)
   

Положительное значение приведенной силы говорит о том, что предварительно выбранное ее направление оказалось верным.

Часто для определения приведенной силы используют графический метод, предложенный Н.Е.Жуковским и названный впоследствии его именем.
Суть метода состоит в следующем.

1. 
   Для заданного положения механизма в произвольном масштабе строят план скоростей. На плане скоростей должны быть изображены скорости всех точек, в которых приложены силы, включая приведенную (заменяющую).
   
2. 
   В соответствующих точках плана скоростей прикладывают силы, перенося их от механизма на план скоростей с поворотом на 90° в заранее выбранную сторону.
   
3. 
   Используя линейку, определяют плечи всех сил относительно полюса плана скоростей и записывают выражения:
   

• 
  для момента приведенной силы;
  
• 
  для суммы моментов заменяемых сил.
  

В обоих случаях используют одинаковое правило знаков. В записанных выражениях неизвестной величиной является только величина приведенной силы.

4. 
   Величину приведенной силы находят из условия равенства этих моментов.
   

Учитывая, что в методе Жуковского приравниваются моменты сил, сам метод в литературе часто называют «рычагом Жуковского».
Попытаемся определить приведенную силу из предыдущего примера, используя рычаг Жуковского. Для этого воспользуемся алгоритмом, изложенным выше.

П лан механизма в заданном положении, силы и план скоростей показаны на рис.6.5.
Тогда:

(6.17)
Сравним полученные результаты.

Как видим, если числитель и знаменатель (6.17) умножить на масштабный коэффициент и учесть, что , то выражения (6.16) и (6.17) становятся тождественными.
Дополнительные замечания к графическому методу определения

1. 
   Иногда в литературе можно встретить иную трактовку метода Жуковского. В ней предлагается повернуть на 90° сам план скоростей, оставив направления сил неизменными. Попробуйте реализовать этот способ для уже решенной задачи (Рис.6.5) и убедитесь, что при повороте сил (первый способ) или повороте плана скоростей (второй способ) уравнения моментов для определения получаются идентичными.
   
2. 
   Приведение сил в задачах аналитической механики – относительно сложная операция. Благодаря «рычагу» Н.Е.Жуковского, процесс нахождения мощностей сил и самой приведенной силы стал технически менее сложным и формально свелся к простому определению моментов сил на плане скоростей.
   

Все гениальное – просто!!!

4. 
   Приведение масс.
   

Второй важной операцией при переходе от механизма к динамической модели является определение ее массовой (инерционной) характеристики.

Как отмечалось ранее (п.6.2), инерционная характеристика начального звена динамической модели в любой момент времени должна быть равна приведенной к начальному звену механизма инерционной характеристике его звеньев.

В зависимости от вида движения начального звена приведенной инерционной характеристикой динамической модели будет приведенная масса (если начальное звено совершает поступательное движение) или приведенный момент инерции (если начальное звено вращается).
Приведенная масса – условная масса начального звена (звена приведения), сосредоточенная в точке приведения звена, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.

Приведенный момент инерции – условный момент инерции начального звена (звена приведения), вычисленный из условия равенства кинетических энергий начального звена и кинетической энергии всех звеньев механизма.
Из определений следует, что приведение масс выполняется на основе равенства кинетических энергий механизма, с одной стороны, и динамической модели (звена приведения) с другой.
Тогда для условного механизма с звеньями б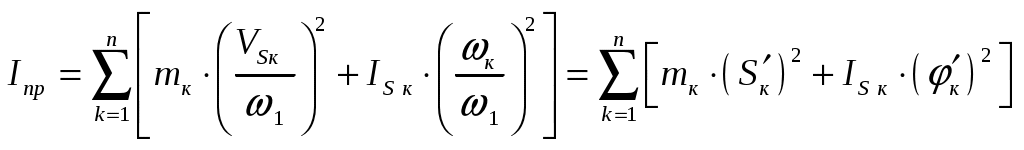удем иметь:
, (6.18)

где , (6.19)

(6.20)
Отсюда

, (6.21)
где - известны; - определяют по планам скоростей.
Если звено приведения совершает поступательное движение, то
, (6.22)

откуда получим 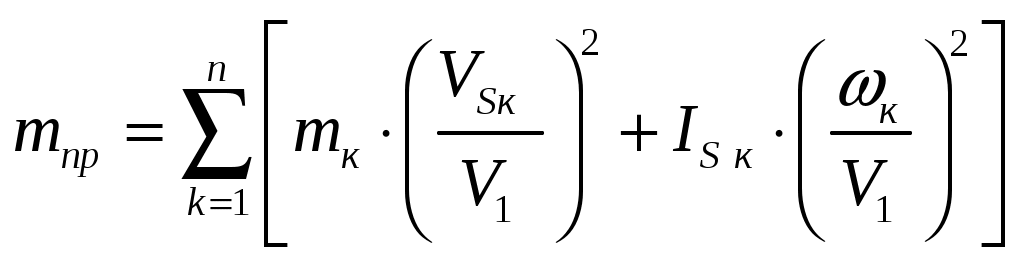(6.23)

5. 
   Уравнение движения машины.
   

Для выявления зависимости между силами, действующими на механизм, и кинематическими характеристиками движения воспользуемся теоремой об изменении кинетической энергии механической системы в дифференциальной форме.
Теорема
Дифференциал кинетической энергии равен сумме элементарных работ всех действующих на механизм сил, т.е.
(6.24)

Аналогично для динамической модели :
(6.25)
Определим дифференциал кинетической энергии динамической модели с вращающимся начальным звеном (с учетом того, что ).

Получим:


(6.26)

К динамической модели приложен приведенный момент. Определим его элементарную работу:

(6.27)
После подстановки (6.15) и (6.16) в (6.14) и сокращения на получаем:
(6.28)
Отсюда уравнение движения машины для вращательного движения условного звена:

(6.29)
В частном случае получаем известное динамическое уравнение для вращательного движения твердого тела.
Если условное звено динамической модели совершает поступательное движение:
(6.30)
В частном случае имеем , т.е. известное динамическое уравнение для поступательного движения твердого тела.

6. 
   Задачи динамического исследования механизмов.
   

Входящие в динамические уравнения движения любого объекта динамические характеристики можно разделить на три группы (Рис.6.6):

1. 
   кинематические (функция положения, скорость, ускорение);
   
2. 
   силовые (силы и моменты сил);
   
3. 
   инерционные (массы звеньев, моменты инерции)
   

Эта закономерность наблюдается, начиная с самых простых ( - для материальной точки) динамических уравнений и до самых сложных. Дифференциальные уравнения, полученные заменой ускорений дифференциальным аналогом, имеют те же свойства. Решить задачу динамики – значит решить указанные уравнения относительно одной группы параметров, задавшись динамическими параметрами двух других групп. В зависимости от того, какие из параметров подлежат определению, а какие задаются, все задачи динамического исследования получили свои названия.




На рис.6.6 в виде структурной схемы изображены группы динамических характеристик и показаны направления решения задач динамики.
Из схемы видно, что:

1. 
   решение задачи относительно силовых характеристик при заданных кинематических и инерционных носит название