Лекции. Лекции ТММ. Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика
 Скачать 5.61 Mb. Скачать 5.61 Mb.
|
|
силовой анализ; при определении кинематических параметров на основании известных силовых и инерционных получают задачу динамического анализа; определение инерционных характеристик на основании известных кинематических и силовых – это задача динамического синтеза. Вопросы для самоконтроля Что называют «работой силы»? Как она вычисляется? В чем измеряется? В каких случаях работа силы является положительной, отрицательной, равной нулю? Нарисуйте тело, лежащее на наклонной плоскости. Какую работу (по знаку и величине) совершит сила тяжести, если тело переместить вниз по плоскости? Под каким углом нужно установить наклонную плоскость, чтобы работа силы тяжести равнялась нулю? Что называют «мощностью силы»? Как она вычисляется? В чем измеряется? В каких случаях мощность силы является положительной, отрицательной, равной нулю? Работа и мощность момента пары сил. Как они вычисляются? От чего зависит знак этих величин? По какому признаку внешние силы, действующие на звенья механизма, классифицируются на движущие, силы сопротивления и безразличные? Какие силы называют силами полезного сопротивления? Какие силы являются силами вредного сопротивления? Приведите примеры. Приведите 2-3 примера, когда трение в механизме выполняет положительную роль. Объясните суть понятия «динамическая модель» механизма. Какими динамическими характеристиками она обладает? Что такое «приведенная сила» («момент сил»)? К какому звену они прикладываются? Как их определяют? Что такое «приведенная масса» («момент инерции»)? Какое звено обладает приведенной массовой характеристикой? Как эта характеристика определяется? Что такое «рычаг Жуковского»? Для чего он используется? Напишите уравнение движения машины, если начальное звено совершает вращательное движение. Объясните все буквенные обозначения, входящие в него. Задачи динамического исследования механизмов можно разделить на «динамический анализ», «динамический синтез» и «силовой анализ». Объясните смысл этих задач (что должно быть задано, а что нужно найти). Лекция 7 динамический анализ механизма (графический метод) Режимы движения механизма. ([1], §64; [2], §4.5) Неравномерность движения начального звена. Средняя скорость. Коэффициент неравномерности. ([1], §82-83; [2], §4.9) Диаграмма «Энергия – масса» при установившемся режиме работы. Порядок построения. ([1], §83; [2], §4.10) Определение мгновенной скорости начального звена. ([1], §83) Определение ускорения начального звена. ([2], §4.10) Режимы движения механизма Полное время движения механизма – отрезок времени от момента начала движения до его полной остановки (для механизма с одной степенью свободы – от начала движения до полной остановки начального звена). На рис.7.1 представлена тахограмма 1 движения механизма, с начальным звеном в виде кривошипа. 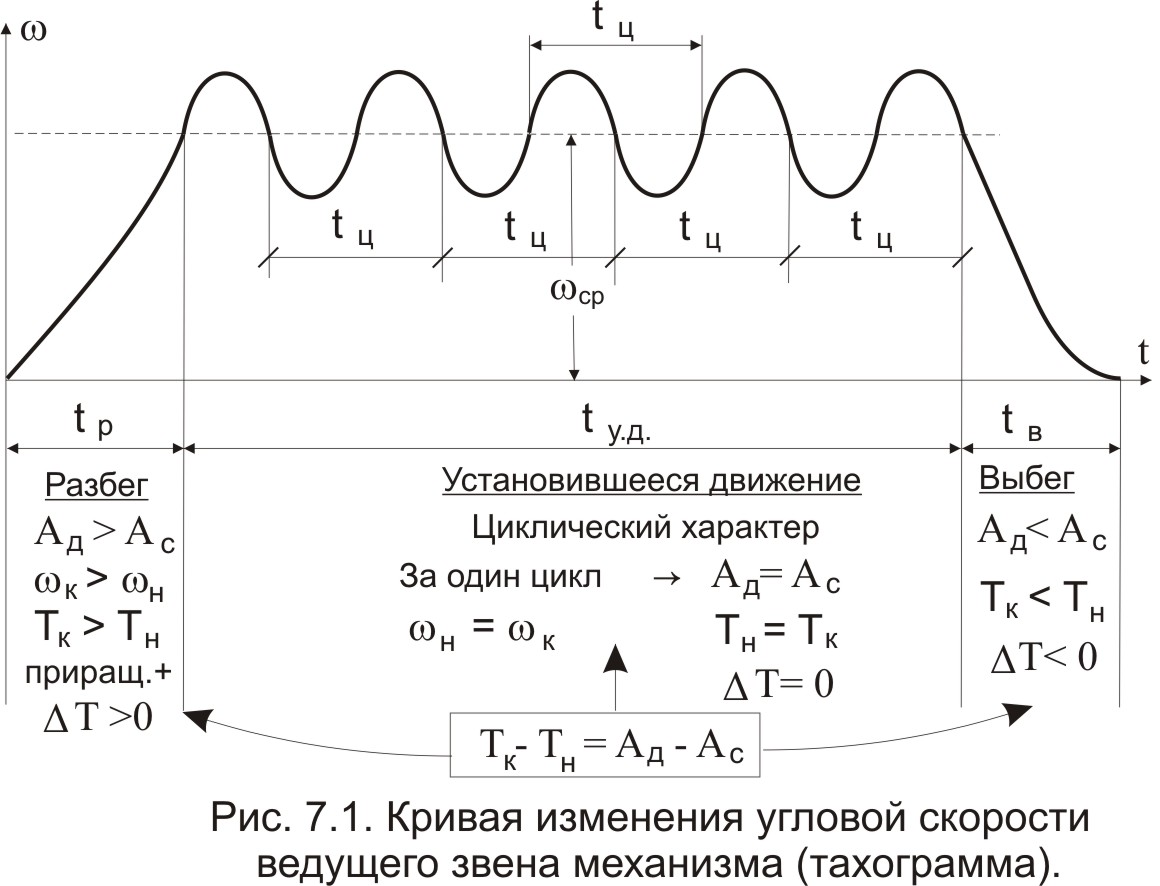 Из графика видно, что в общем случае полное время движения можно разделить на три части: Время разбега – характеризуется увеличением скорости начального звена от нуля до некоторого среднего (номинального) значения рабочей скорости. Время установившегося движения – характеризуется периодическим изменением скорости начального звена около среднего значения рабочей скорости. При этом все кинематические характеристики начального звена (положение кривошипа, его угловая скорость, угловое ускорение) - периодические функции. Кинетическая энергия механизма во времени изменяется также по периодическому закону. Промежуток времени, по истечении которого положение начального звена, его скорость и ускорение, а также кинетическая энергия механизма принимают первоначальные значения и затем начинают периодически повторяться – называют циклом установившегося движения. Время выбега – характеризуется убыванием скорости начального звена от средней рабочей скорости до полной остановки. На диаграмме (Рис.7.1) использованы следующие обозначения: В рамке под диаграммой приведено выражение теоремы об изменении кинетической энергии механизма для времени полного цикла (интегральная форма теоремы). Из теоремы следует, что при Неравномерность движения начального звена. Средняя скорость. Коэффициент неравномерности Часто на вопрос о характеристиках движения механизма в установившемся режиме работы студенты отвечают: «Это режим работы, при котором все показатели выходят на номинальный рабочий уровень, т.е. стабилизируются». Это неверный ответ. Из предыдущего параграфа (п.7.1) следует, что угловая скорость начального звена в установившемся режиме изменяется, т.е. движение начального звена является неравномерным. В чем же причина такой неравномерности? Для анализа этого явления решим уравнение (6.29) относительно углового ускорения: 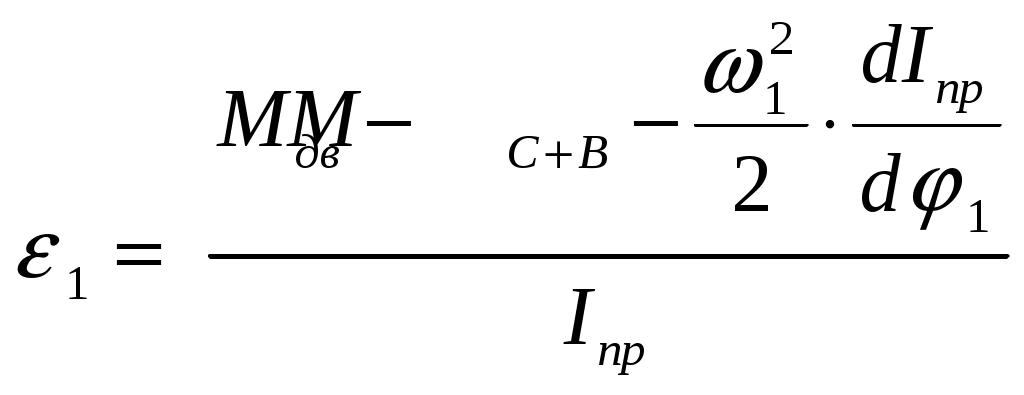 , (7.1) , (7.1)Из (7.1) видно, что угловое ускорение Из трех составляющих числителя (7.1) только движущий момент Приведенный момент сил сопротивления и веса Третья составляющая содержит приведенный момент инерции механизма Обобщив результаты анализа, приходим к выводу, что неравномерность движения начального звена для рычажных механизмов - явление не просто возможное, а скорее – обычное и закономерное. Причинами неравномерности следует считать: изменение сил сопротивления при движении механизма (смотри, например, график сил трения в поступательной паре ползун-стойка в курсовом проекте); различное влияние сил тяжести звеньев (при опускании центров масс звеньев, силы тяжести являются движущими силами и, наоборот, при их подъеме – силами сопротивления); сложный характер изменения приведенного момента инерции механизма (что означает изменение величины и направления сил инерции звеньев). Неравномерность движения количественно оценивается по величине коэффициента неравномерности ( Д 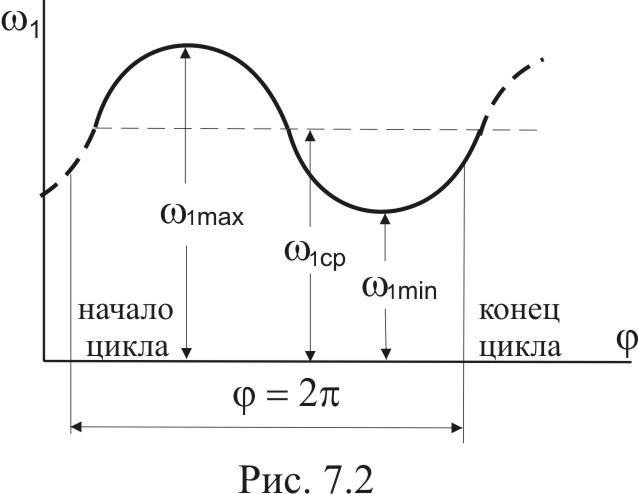 ля вывода расчетной формулы введем понятия максимальной, минимальной и средней скорости начального звена. ля вывода расчетной формулы введем понятия максимальной, минимальной и средней скорости начального звена. Рассмотрим изменение угловой скорости начального звена за один цикл установившегося движения (Рис.7.2). Наибольшую скорость в цикле будем считать максимальной (1max), а наименьшую – минимальной (1min). Среднюю угловую скорость звена найдем приближенно, как полу-сумму 1max и 1min : 1 Коэффициент неравномерности численно определяется отношением амплитуды изменения угловой скорости (1max - 1min) к величине средней скорости 1ср, т.е.: 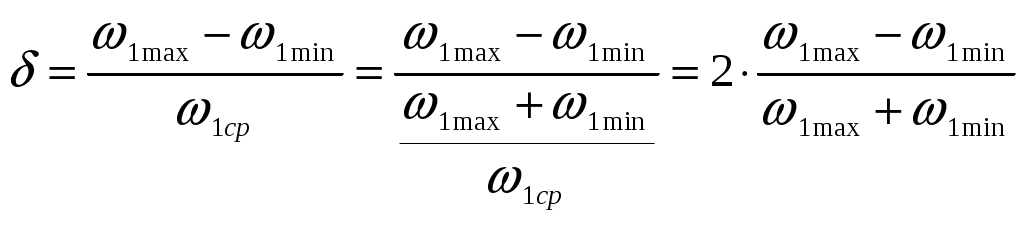 (7.3) (7.3)Теоретические пределы изменения Нижний предел (т.е. Второй предел (т.е. Неравномерность движения для механизмов и машин - явление нежелательное. Она ведет к появлению целого ряда негативных факторов. Так, возникающие при изменении скорости ведущего звена дополнительные ускорения всех звеньев вызывают добавочные динамические нагрузки в кинематических парах и элементах привода механизма. Кроме того, в связи с неравномерностью могут возникать дополнительные колебания звеньев, отрицательно влияющие на динамику и ресурс работы машины. В силу этих причин, от неравномерности стремятся если не избавиться полностью, то хотя бы уменьшить. Одно из решений в данном случае – установка маховика (см. Лекции по ТММ, Часть 2, Лекция 8). Значения Насосы, сельскохозяйственные машины, конвейеры . . . . . . . . . 0,20,1 Металлообрабатывающие станки, двигатели внутреннего сгорания (ДВС) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,020,01 Электродвигатели, генераторы . . . . . . . . . . . . . . . . . . . . . . . . . 0,010,005 Авиационные двигатели, турбогенераторы . . . . . . . . . . . . меньше 0,005 Из таблицы видно, что более быстроходным машинам соответствуют меньшие значения коэффициента Диаграмма “Энергия - масса” при установившемся режиме работы. Порядок построения. Диаграмма “Энергия - масса” (диаграмма Виттенбауэра) – графическая зависимость приращения кинетической энергии механизма ( Δ Диаграмма может быть использована: для определения коэффициента неравномерности для подбора маховика с целью снижения для определения текущего значения угловой скорости начального звена 1. Построение диаграммы выполняется в несколько этапов: Рассматривают 1 цикл установившегося движения (для кривошипно-ползунного механизма в курсовом проекте - 1ц =2 ). Соответствующий циклу угол поворота начального звена делят на  Построение графика приведенного к начальному звену момента инерции механизма Построение графика приведенного к начальному звену момента инерции механизма Значения I пр0, I пр1 … I прn определяют расчетным путем для всех положений механизма по формуле (6.21) (см. Лекцию 6, п.6.4).  Построение графика изменения приведенного к начальному звену момента сил сопротивления и веса Построение графика изменения приведенного к начальному звену момента сил сопротивления и веса Ординаты графика 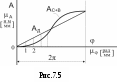 Построение графиков работ момента сил сопротивления и веса и движущего момента Построение графиков работ момента сил сопротивления и веса и движущего момента Построение графиков сводится к графическому интегрированию функций: Вторая из функций ( Движущий момент принят постоянным, т.е. Работы движущих сил и сил сопротивления за один цикл установившегося движения равны между собой, т.е. 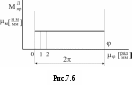 Построение графика изменения приведенного к начальному звену движущего момента Построение графика изменения приведенного к начальному звену движущего момента Движущий момент, приведенный к кривошипу, определяют из условия равенства площадей графиков 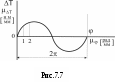 Построение графика приращения кинетической энергии Δ Построение графика приращения кинетической энергии ΔГрафик Δ 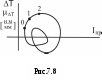 Построение диаграммы “Энергия - масса” Построение диаграммы “Энергия - масса” Диаграмма Определение мгновенной скорости начального звена. На рис.7.9 приведена диаграмма “Энергия - масса” в двух системах координат: внутренняя система 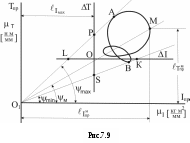 Динамическая модель механизма – вращающийся кривошип. Кинетическая энергия динамической модели: отсюда: При помощи (7.4) можно определить мгновенное значение угловой скорости начального звена для любого положения (т.е. любой точки на диаграмме Определение ускорения начального звена Для определения углового ускорения 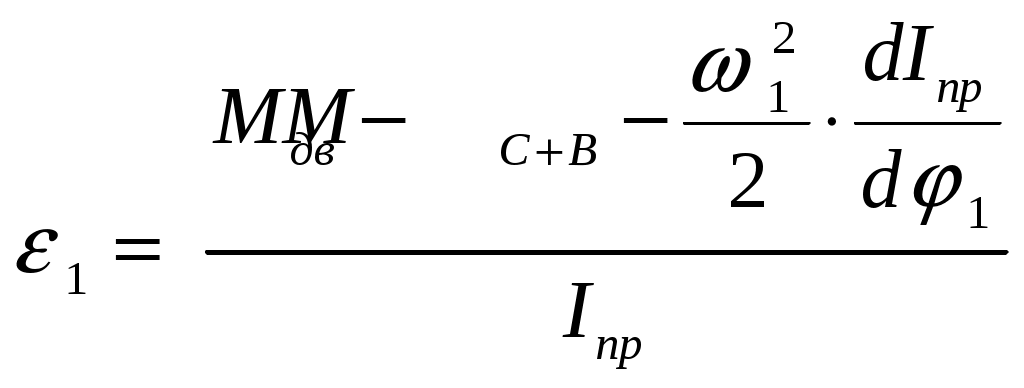 (7.6) (7.6)При этом параметры для вычисления берут из соответствующих графиков для соответствующего положения механизма (угла При необходимости угловое ускорение Вопросы для самоконтроля Назовите основные режимы движения механизмов? Чем с энергетической точки зрения отличаются режимы разбега и выбега? Что называют циклом установившегося движения? Верно ли утверждение «В режиме установившегося движения параметры механизма выходят на номинальный уровень и стабилизируются»? В чем причина неравномерности движения механизма при установившемся режиме работы? Как вычисляют среднюю скорость начального звена при установившемся режиме работы механизма? Как вычисляют коэффициент неравномерности? Каковы пределы его изменения? Назовите приближенные значения коэффициентов неравномерности для сельскохозяйственных машин, металлорежущих станков, турбин. Чем можно объяснить различный порядок этих значений? По какой формуле можно определить мгновенную угловую скорость начального звена, если диаграмма «Энергия-масса» задана? По какой формуле находят угловое ускорение начального звена? Литература Артоболевский И.И. Теория механизмов и машин: Учеб. для втузов.- 4-е изд. – М.: Наука. Гл. ред. физ.-мат. лит., 1988.- 640 с. Теория механизмов и машин: Учеб. для втузов/ К.В.Фролов, С.А.Попов, А.К.Мусатов и др.; Под ред. К.В.Фролова.- М.: Высш. шк., 1987.- 496 с. Левитская О.Н., Левитский Н.И. Курс теории механизмов и машин: Учеб. пособие для мех. спец. вузов.- 2-е изд., перераб. и дополн.- М.: Высш. шк., 1985.- 279 с., ил. Теория механизмов и машин. Терминология. Буквенные обозначения величин.- М.: Наука, 1984.- Вып.99. 1 Имеются в виду задачи кинематики и динамики механических систем. 1 Здесь преобразование материалов понимается как формоизменение, механическая обработка или перемещение объектов, на которые направлено действие машины. 1 В ТММ под твердыми телами понимают как абсолютно твердые, так и деформируемые и гибкие тела [4]. Другими телами, входящими в состав механизма, могут быть жидкие или газообразные тела (если речь идет о гидравлических или пневматических механизмах) 1 Неподвижность звена может быть условной (относительной). Так бывает, если корпус механизма установлен на подвижном основании. 2 В литературе по структуре механизмов стойке обычно присваивают номер « 0 » (нулевое звено). 3 Термины «входное звено» и «выходное звено» в литературе по структуре механизмов появились сравнительно недавно. Ранее эти звенья называли соответственно «ведущим» и «ведомым». Введение новых названий стало необходимым по причине их неоднозначной трактовки в задачах структурного и динамического исследования. В задачах структурного анализа ведущим и ведомым звеном называли собственно входное и выходное звенья механизма. В задачах динамики механизмов руководствуются другим подходом. Здесь под ведущим звеном понимают звено, к которому приложены внешние силы, сумма элементарных работ которых является положительной. Эти силы, следовательно, классифицируются как движущие (отсюда название звена – ведущее). При изменении знака элементарной работы внешних сил то же звено попадает в разряд ведомых. Таким образом, термины «входное звено» и «выходное звено» являются более подходящими для исследования структуры механизмов. 1 Деление кинематических пар на высшие и низшие является условным, т.к. линейный или точечный контакт элементов пар в реальных условиях является невозможным по причине деформируемости элементов. 1 |
