Лекции. Лекции ТММ. Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика
 Скачать 5.61 Mb.
|
|
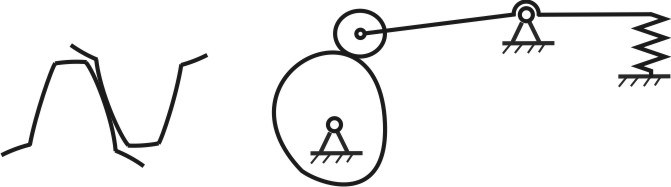
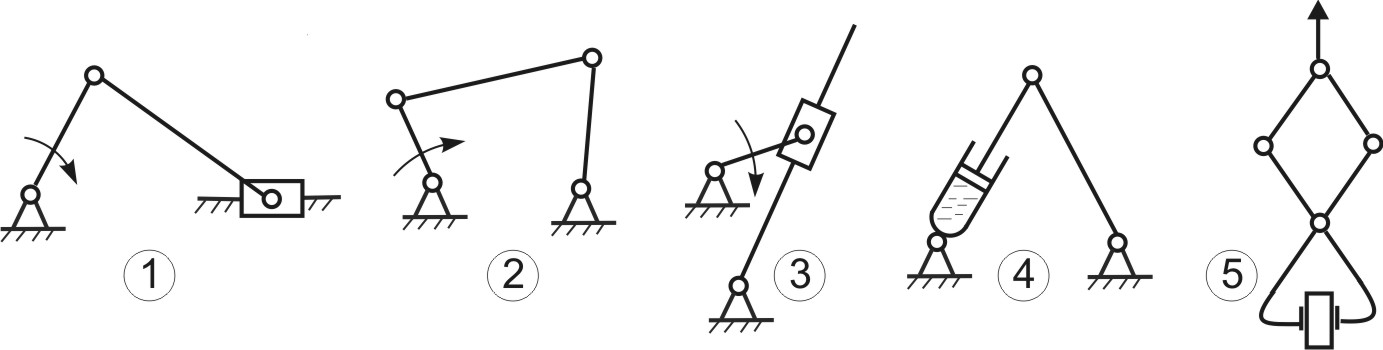
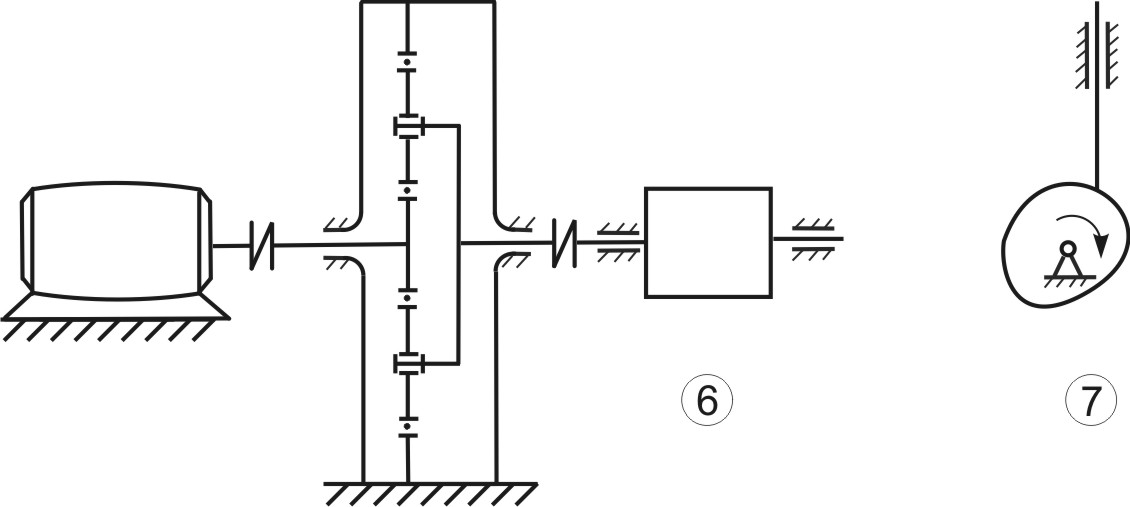
Плоским механизмом называют механизм, все точки которого двигаются в плоскостях, параллельных одной какой-либо плоскости. Такие механизмы нашли широкое распространение и используются во многих машинах, станках и приспособлениях. Звенья механизмов соединяются подвижно, образуя между собой низшие и высшие кинематические пары. Смысл этих понятий подробно изложен в лекции 1 (п.1.3). На рис.3.1,а изображены примеры этих пар, наиболее часто встречающиеся в механизмах. Здесь же (Рис.3.1,б) приведены схемы некоторых плоских механизмов, в состав которых входят низшие и высшие пары.
1 – кривошипно-ползунный механизм; 2 – кривошипно-коромысловый механизм; 3 – кривошипно-кулисный механизм; 4 – механизм с пневмо- или гидроцилиндром; 5 – грузозахватное приспособление клещевого типа; 6 –планетарный механизм редуктора в главной линии привода конвейера; 7 – кулачковый механизм Рис.3.1 Низшим и высшим парам присущи определенные достоинства и определенные недостатки. Поэтому вопрос о том, какие пары «лучше» решается в зависимости от конкретных условий задачи. Рассмотрим, например, низшие пары. Их достоинства и недостатки обусловлены свойствами низших пар, а, именно, тем, что контакт между элементами пары осуществляется по поверхности 1. Отсюда вытекают преимущества низших пар: 1) удельное давление и износ низших пар (вследствие контакта по поверхности) меньше, чем аналогичный показатель у высших; изготовление элементов пар достаточно простое и точное; не требуется дополнительных приспособлений, обеспечивающих замыкание элементов пар (в низших парах - обычно геометрическое замыкание; в высших парах – обычно силовое, т.е. за счет дополнительного прижатия) В то же время, недостатками низших пар являются следующие: механизм, созданный на базе низших пар, имеет более сложную структуру, т.е. большее число звеньев и большее число кинематических пар; большие габаритные размеры механизма; повышенные затраты на преодоление трения в парах, а, значит, низкий КПД механизма Высшие кинематические пары, в сравнении с низшими, имеют прямо противоположные свойства, т.е. не обладают преимуществами низших пар, зато лишены их недостатков. Задачи структурного и метрического синтеза. Основной задачей структурного синтеза механизма является выбор его принципиальной схемы. Задача осуществляется в 2 этапа: Создание ряда принципиальных схем механизмов, удовлетворяющих требуемому движению входного и выходного звеньев. Выбор конкретной схемы, исходя из критериев (мощность привода, компактность, быстродействие, нагруженность кинематических пар, их износ, КПД механизма, стоимость изготовления, срок окупаемости и т.д.) Удовлетворить требованиям всех критериев одновременно – задача невыполнимая. Поэтому ограничиваются анализом альтернативных схем механизма по критериям, принятым в качестве приоритетных. В курсовом проекте по ТММ эта часть инженерной работы студентами не выполняется, т.к. принципиальная схема механизма задается по условию. Алгоритм структурного синтеза механизма проиллюстрируем простым примером. П  усть поставлена технологическая задача - спроектировать механизм для пошагового перемещения прямоугольных заготовок в проходной нагревательной печи. Данный механизм (Рис.3.2) может применяться в цехах горячей прокатки листа и называется механизмом «безударной» выдачи слябов. Задача механизма – переместить лежащий в методической печи сляб на приемный рольганг стана горячей прокатки. В качестве машины-двигателя планируется использовать электродвигатель. Поэтому, за входное звено механизма принимаем кривошип, за выходное звено - ползун. Нарисуем несколько возможных схем механизмов с входным кривошипом и выходным ползуном (Рис.3.3) 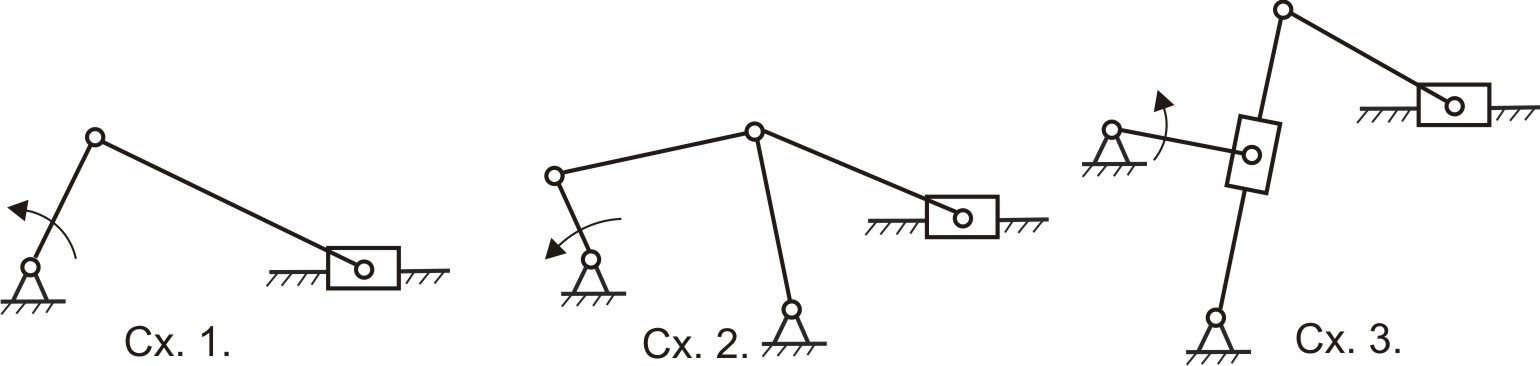 Рис.3.3 Все эти схемы удовлетворяют исходному условию по характеру движения входного и выходного звеньев. Какой же механизм выбрать? Задачей структурного синтеза является анализ предложенных вариантов механизмов и выбор наиболее удачной схемы, с точки зрения технических и эксплуатационных характеристик. Для данного случая наиболее рациональной является схема 2. Она и получила практическое воплощение в ряде цехов прокатного производства, как структурная схема «Механизма безударной выдачи слябов». Метрический синтез можно считать одной из частных задач кинематического синтеза механизма, поскольку речь идет о создании механизма с заранее заданными геометрическими свойствами. Задачей метрического синтеза (для выбранной принципиальной схемы) является определение длин звеньев механизма, при которых удовлетворяются критерии метрического синтеза (критерий существования кривошипа, критерий положений ведомых звеньев, критерий максимальных углов давления, критерий рационального использования мощности привода и др.). Рассмотрим суть этих критериев более подробно. Критерий существования кривошипа. Кривошипно-коромысловый механизм часто используется как самостоятельный, либо как часть более сложного механизма. Ведущим звеном этого механизма является кривошип, т.е. звено, выполняющее вращательное движение с углом поворота 360. Понятно, что с геометрической точки зрения, это возможно только при определенных соотношениях длин звеньев. Определим эти соотношения. Д 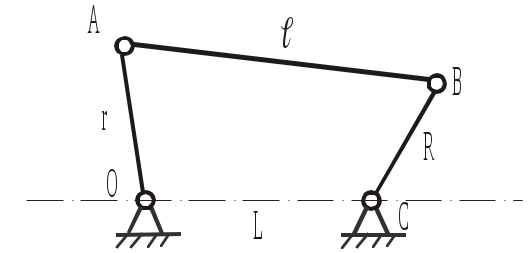 ано: Принципиальная схема кривошипно-коромыслового механизма (Рис.3.4). Звено ОА = r – кривошип; звено АВ = l – шатун; звено СВ = R - коромысло; ОС = L – расстояние между неподвижными точками стойки.Определить: соотношение размеров звеньев механизма, при котором кривошип ОА может выполнить полный оборот. Рис. 3.4 Эту задачу в литературе иногда называют «условием проворачиваемости» кривошипно-коромыслового механизма или «условием Грасгофа». Решение. Рассмотрим механизм ОАВС в крайних положениях (Рис.3.5), когда коромысло ВС временно останавливается, меняя направление движения. При этом СВл – крайнее левое положение коромысла, СВп – крайнее правое его положение. 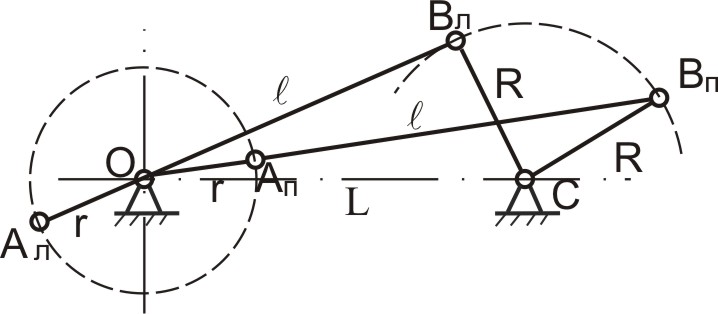 Из Δ ОВлС   (3.1)  (3.2)Из Δ ОВпС  (3.3)Рис. 3.5 \ Выполним преобразования: (3.1) (r+R) < L+ (3.4) (3.2) (r+L) < R+ (3.5) Из (3.3), (3.4) и (3.5) следует первое условие: Условие 1. В кривошипно-коромысловом механизме сумма длин кривошипа и любого другого звена всегда меньше суммы длин других звеньев. Продолжим преобразования. Сложим выражения (3.3),(3.4) и (3.5) почленно. Получим: 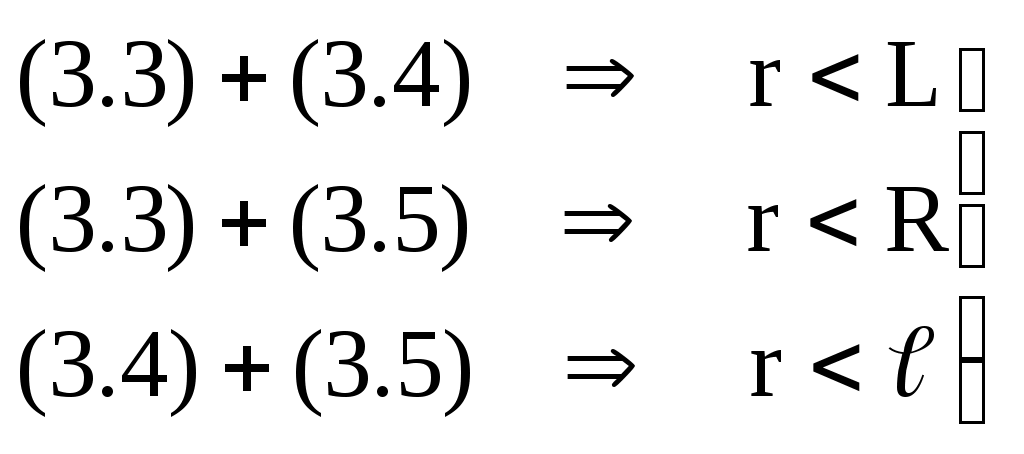 (3.6)Условие 2. В кривошипно-коромысловом механизме кривошип – самое короткое звено. Выполнение этих 2-х условий гарантирует проворачиваемость механизма, т.е. возможность поворота кривошипа на 360. Критерий положений ведомого звена Смысл критерия заключается в определении соотношений между длинами звеньев, при которых обеспечиваются заданные положения выходных звеньев (в данном случае заданные крайние положения). Ориентируясь на схемы заданий к курсовому проекту, рассмотрим примеры расчета длин звеньев применительно к кривошипно-коромысловому и коромыслово-ползунному механизмам. Оба механизма являются частями главного исполнительного механизма качающегося конвейера. Пример 1 Д 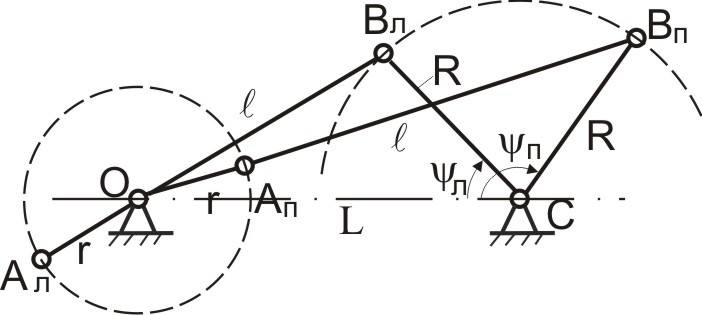 ано: Кривошипно-коромысловый механизм (Рис.3.6); выходное звено – коромысло СВ; заданы размеры СВ=R, л , п, ОС=L.Определить: длины звеньев ОА = r, АВ = , обеспечивающие углы л , п в крайних положениях коромысла СВ. Рис. 3.6 Решение. Рассмотрим механизм в крайних положениях (Рис.3.6). Применив теорему косинусов, получим: Для  (3.7)Для  (3.8)Сложим почленно (3.7) + (3.8) и решим равенство относительно :  (3.9)Вычтем почленно (3.8) - (3.7) и решим равенство относительно  : (3.10)Система 2-х уравнений (3.7) - (3.8) содержит 6 независимых геометрических параметров. Это значит, что можно найти 2 любых параметра, если остальные 4 заданы (причем в любых комбинациях). Так, например, в курсовом проекте: задаются - r, L, л, п, а подлежат определению - , R. Пример 2 Д  ано: Коромыслово-ползунный механизм (Рис.3.7); выходное звено – ползун; заданы размеры л = п = , S.Определить: длину звена СВ = R, обеспечивающую перемещение ползуна на расстояние S. Решение. Из рис.3.7 следует:  (3.11)Заметим, что выражение (3.11) справедливо для произвольного значения ВD. Критерий максимального угла давления На рис.3.8 изображена кинематическая пара, образованная шатуном 1 (ведущее звено) и ползуном 2 (ведомое звено). Угол давления в кинематической паре шатун-ползун – это угол 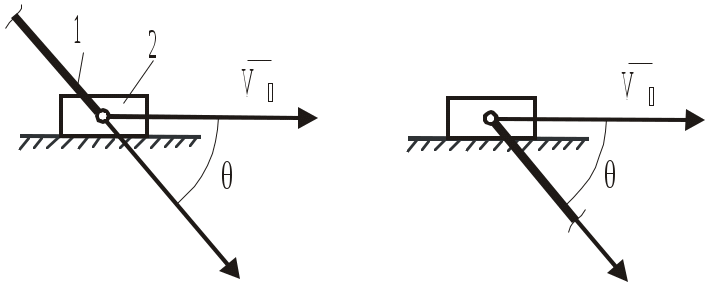 между направлением скорости ползуна  и направлением силы давления шатуна на ползун. Известно, что (при невесомом шатуне) эта сила давления будет направлена вдоль шатуна (если шатун криволинейный – то по прямой, соединяющей концевые шарниры звена).У  гол давления имеет большое значение для работоспособности механизма и его КПД. Большие углы давления приводят к повышенной силе трения между ползуном и направляющей стойки. Это влияет на равномерность движения механизма, степень износа подшипников, а иногда приводит к полной остановке механизма вследствие заклинивания. Рис.3.8 Н  а рис.3.9 изображен ползун, входящий в кинематические пары с шатуном и стойкой. Сила  давления шатуна на ползун, разложена на составляющие  и  . Касательная составляющая  обеспечивает перемещение ползуна вдоль стойки и совершает положительную работу, т.е. является полезной движущей силой. Нормальная составляющая , направленная перпендикулярно, работу по перемещению ползуна не совершает. Напротив, именно эта сила нормального давления определяет величину силы трения между ползуном и стойкой. Действительно, из условия равновесия сил в направлении нормали к направляющей получаем нормальную реакцию стойки  = - . Далее, на основании закона Кулона, имеем  . А отсюда следует, что с увеличением возрастает  , а вместе с ней и  . Следует иметь ввиду, что угол давления  - не постоянная величина, а изменяется в зависимости от положений механизма.Угол давления можно уменьшить, если увеличить размеры соответствующих звеньев механизма. При этом габаритные размеры самого механизма увеличиваются, что не всегда приемлемо.Таким образом, оптимальным вариантом метрического синтеза является тот, когда угол давления в наиболее неблагоприятных положениях механизма достигает максимально допустимого значения, но не превышает его. При создании новых механизмов максимальный угол давления в паре шатун-ползун рекомендуется принимать равным max = 3040. Покажем на примере, как определяется длина звена по критерию «угол давления». Пример. Н  а рис.3.10 изображен кривошипно-ползунный механизм с направляющей, смещенной относительно центра вращения кривошипа на величину эксцентриситета - е*. Заданы длина кривошипа ОА и максимальный угол давления в паре шатун-ползун - max.Дано: ОА= r, max, е*. Определить: длину шатуна , из условия, что при полном обороте кривошипа угол давления не превысит max. Решение. Рассмотрим изменение угла давления в паре шатун-ползун при прямом и обратном движении ползуна. На рисунке сделаны обозначения:  - угол давления при прямом ходе; - угол давления при обратном ходе.Из геометрии следует:  (3.12)  (3.13)Анализируя (3.12) и (3.13) , находим положения механизма, при которых значения углов давления максимальны:  и  при  (т.е. ОА - вертикально).Значит:  (3.14)  (3.15)Учитывая, что  принимаем  Поэтому окончательно:  (3.16)Критерий отношения средних скоростей ведомого звена Иногда при проектировании механизмов бывает важно, чтобы выходное звено на рабочем и на холостом ходу двигалось с различными средними скоростями.1 В этом случае метрический синтез механизма выполняется с учетом коэффициента отношения средних скоростей. 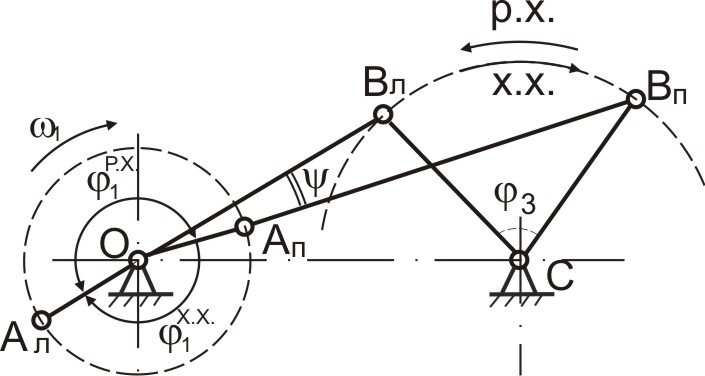 Рассмотрим работу кривошипно-коромыслового механизма (рис. 3.11). Стрелками на рисунке обозначены: р.х.– рабочий ход ведомого звена (совершается полезная работа); х.х. – холостой ход (полезная работа не совершается). Предположим, что ведущее звено ОА вращается равномерно (1=const). Рис.3.11 Из рис. 3.11 видно, что  , т.е.  Коэффициент отношения средних скоростей ведомого звена:  (для реальных механизмов, типа конвейеров = 1.1 …1.3) . Это следует из соотношения  Для ведущего звена  Отсюда  Имея требуемое значение  , находят угол  , после чего на основании рис.3.11 определяют необходимые длины звеньев.Метрический синтез сложного механизма Сложным механизмом условно будем называть механизм, в состав которого входят несколько структурных групп. Пример такого механизма показан на рис.3.12. Структурно он состоит из первичного механизма и двух последовательно присоединенных к нему структурных групп. 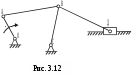 Как и в случае простых механизмов, метрический синтез сложного механизма осуществляется с использованием рассмотренных выше или иных критериев. При этом вначале сложный механизм разбивается на более простые механизмы в соответствии с формулой строения. В нашем случае это механизмы ОАВС и СВД. Метрический синтез сложного механизма выполняют в последовательности: синтез первого простого механизма; синтез второго простого механизма; и т.д. Для закрепления изложенного материала, рассмотрим последовательность операций по метрическому синтезу механизма качающегося конвейера из курсового проекта по ТММ. Предположим, что принципиальная схема механизма задана и изображена на рис.3.13. Решение:  Выделяем простые механизмы: ОАВС и СДЕ. Используем критерий положений коромысла СВ. Дано:  .Используем критерий положений ползуна Е. Дано:  .Критерий максимального угла давления в кинематической паре Е -  .Дано:  . Критерий отношения средних скоростей выходного звена Дано: крайние положения механизма, угол направление вращения ведущего звена. Вопросы для самоконтроля Какие механизмы в ТММ называют плоскими? Нарисуйте несколько принципиальных схем плоских механизмов. Покажите низшие и высшие кинематические пары, использованные в них. Укажите достоинства и недостатки низших и высших кинематических пар. Объясните смысл задачи структурного синтеза механизма. Что при этом задается, а что подлежит определению? Объясните смысл задачи метрического синтеза механизма. Что при этом задается, а что подлежит определению? Лекция 4 |
