Лекции. Лекции ТММ. Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика

• Название: Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика
• Анкор: Лекции
• Дата: 16.01.2023
• Размер: 5.61 Mb.
• Имя файла: Лекции ТММ.doc
• Тип: Лекции; #888798
• страница: 6 из 9

кинематический анализ плоских рычажных механизмов (аналитический метод)

1. 
   Определение положений механизма. ([1], §23, 24, 25; [2], §3.3)
   
2. 
   Определение скоростей точек и угловых скоростей звеньев механизма. ([1], §23, 24, 25; [2], §3.3)
   
3. 
   Определение ускорений точек и угловых ускорений звеньев механизма. ([1], §23, 24, 25; [2], §3.3)
   
4. 
   Кинематический анализ сложных механизмов. ([1], §26; [2], §3.3)
   

Кинематический анализ механизмов аналитическим методом выполняется с помощью ПК или другой вычислительной техники. Для этого составляется соответствующая программа вычислений, в которую входят формулы для определения положений звеньев и их кинематических характеристик. Если механизм имеет степень подвижности, равную 1, то все кинематические параметры должны определяться исходя из одной величины – обобщенной координаты (для механизмов с ведущим кривошипом, исходя из положения кривошипа).

В основу аналитического решения задачи положен метод замкнутых векторных контуров, предложенный В.А.Зиновьевым.¹

Покажем получение основных формул кинематического анализа на примере шарнирного четырехзвенника (Рис.5.1).

1. 
   Определение положений механизма.
   

Д 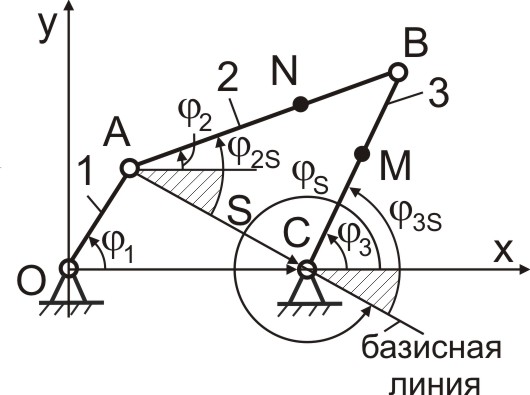ано:
ОА, АВ, ВС, ОС (Рис.5.1);

 ₁ – положение начального звена 1;

₁ – угловая скорость звена 1;

₁ –угловое ускорение звена 1.
Определить:
₂(₁), ₃(₁) - ?

Рис. 5.1.

Решение

1. 
   Выберем систему координат хоу с началом в точке О (Рис.5.1).
   

Рассмотрим векторный контур ОАС, в котором
(5.1)

Принимая , попытаемся определить зависимости и .
Для этого спроецируем (5.1) на оси х и у:
пр.х  (5.2)

пр.y  (5.3)
При этом и - неизвестные параметры.
Выполним преобразования, разделив (5.3) на (5.2):
(5.3) : (5.2)  , (5.4)

т.е. получили зависимость .
Продолжим преобразования с выражениями (5.3) и (5.2):
 (5.5)
т.е. получили зависимость .

2. 
   Рассмотрим векторный контур и определим и .
   

, (5.6) , (5.7)
В (5.6) и (5.7) известно все, кроме _2S и _3S, которые легко определить.
, (5.8)
т.е. получена зависимость .
, (5.9)
т.е. получена зависимость .

3. 
   Определим и .
   

; (5.10)

; (5.11)
Отсюда : ,т.е. имеем ; (5.12)
, т.е. (5.13)
Таким образом, в результате выполнения пп. 1÷3 определено и , т.е. положение звеньев, как функция, положения ведущего звена.

4. 
   При необходимости можно определить положение точек, принадлежащих звеньям 2 или 3 (например, координаты и , - см. рис.5.1). Покажем эту возможность.
   

Найдем проекции положения точек М и N на оси х и у:
(5.14)

(5.15)
(5.16)

(5.17)
Поскольку , то полученные выше формулы позволяют найти , , , , , .
Задача определения положений звеньев и точек звеньев в функции от угла поворота выполнена.

2. 
   Определение скоростей точек и угловых скоростей звеньев механизма.
   

Скорости точек и угловые скорости звеньев можно найти через соответствующие аналоги скоростей:
, (5.18)

где - аналог угловой скорости звена 2; (5.19)

, (5.20)

где - аналог угловой скорости звена 3; (5.21)

При этом и не зависят от ₁.
Таким образом, чтобы найти и , достаточно найти аналоги и .
Определим аналоги угловых скоростей, используя метод замкнутых векторных контуров:
Контур ОАВС (Рис.5.1)
(5.22)
Спроецируем (5.22) на оси х и у:
пр. х  (5.23)

пр. у  (5.24)
Возьмем производную по , учитывая, что и

(5.25)

(5.26)
Если выполнить  (5.25)  cos ₃ + (5.26)  sin ₃ , получим:
(5.27)

Отсюда:

, т.е. (5.28)
Если выполнить  (5.25)  cos ₂ + (5.26)  sin ₂ , аналогично получим:

(5.29)

Откуда:

, т.е. (5.30)
Если известны аналоги (5.28) и (5.30), легко определить ₂ и ₃ из (5.18) и (5.20).

Определим скорости точек
Начнем с простого – точка В и точка М.
; (5.31)

; (5.32)
(5.33)
Скорость точки N вычислим по проекциям:



; (5.34)


(5.35)
(5.36)
По аналогии с введенными ранее понятиями аналогов угловых скоростей можно ввести понятия аналогов скоростей точек А, В, М, N.

; (5.37)

; (5.38)

; (5.39)

(5.40)

2. 
   Определение ускорений точек и угловых ускорений звеньев механизма.
   

Для определения ускорений используют аналоги ускорений:
;
, (5.41)

где - аналог углового ускорения звена 2. (5.42)

Аналогично:

, (5.43)

где - аналог углового ускорения звена 3.

Таким образом, для определения ₂ и ₃ необходимо найти аналоги
Определим аналоги угловых ускорений (Рис. 5.1).

Продифференцируем уравнения (5.25) и (5.26) по ₁, учитывая, что ₂(₁), ₃(₁), .


= ; (5.44)


; (5.45)
Если выполнить  , получим:

; (5.46)
(5.47)
Если выполнить  , получим:

(5.48)
(5.49)
Зная аналоги скоростей и аналоги ускорений, по формулам (5.41) и (5.43) находят ₂ и ₃.

Ускорения точек, принадлежащих звеньям 1 и 3 (в нашем случае точки А, В, М ) находят по формуле:

, (5.50)

где - ускорение - той точки;

- расстояние - той точки от оси вращения;

и - угловое ускорение и угловая скорость -го звена, которому принадлежит -я точка.

В качестве примера, определим ускорение точки В:
Ускорение точки N , принадлежащей звену 2, находят по проекциям, дифференцируя еще раз выражения и .

2. 
   Кинематический анализ сложного механизма.
   

Д ано: ОА – ведущее звено;
ОА, АВ, ВС, ОС, BD (Рис.5.2);

 ₁ – положение ведущего звена;

₁ – угловая скорость ведущего

звена;

₁ –угловое ускорение ведущего

звена.

Определить: _i , V_k , _i , a_k , _i .

Рис. 5.2.
Кинематический анализ сложного механизма выполняется в последовательности, соответствующей написанию формулы строения механизма. В данном случае из формулы строения I(0,1)  II(2,3)  II(4,5) следует, что вначале необходимо определить кинематические характеристики ведущего звена 1. Затем рассматривают векторный контур ОАВС, определяя кинематические характеристики звеньев и точек двухповодковой группы II(2,3). После этого из векторного контура СВD определяют кинематические параметры следующей двухповодковой группы II(4,5).
В заключении следует подчеркнуть, что решение задачи кинематического анализа на ПК, хоть и обладает потенциально более высокими возможностями и точностью, все же само по себе не гарантирует правильного решения. В этой связи составленная компьютерная программа перед ее серьезным использованием должна быть опробована и отлажена на ряде тестовых задач, ответы на которые уже имеются.

Вопросы для самоконтроля

1. 
   В чем Вы видите преимущества аналитического метода кинематического расчета механизма в сравнении с графическим?
   
2. 
   Объясните смысл понятий «аналог угловой скорости», «аналог углового ускорения».
   
3. 
   Объясните смысл метода «замкнутых векторных контуров» при аналитическом решении задачи кинематического анализа.
   
4. 
   В какой последовательности выполняется кинематический анализ сложного рычажного механизма?
   

Лекция 6