Главная страница
Навигация по странице:

  • Правило 1

  • П равило 2

    		•

    Лекции. Лекции ТММ. Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика


    Скачать 5.61 Mb.
    НазваниеЛекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика
    АнкорЛекции
    Дата16.01.2023
    Размер5.61 Mb.
    Формат файлаdoc
    Имя файлаЛекции ТММ.doc
    ТипЛекции
    #888798
    страница5 из 9
    1   2   3   4   5   6   7   8   9
    кинематический анализ плоских рычажных механизмов (графический метод)



      1. Основная задача и цели кинематического анализа. Методы решения. ([1], §14, п.1; §15, п.1; [2], §3.2; [3], Глава 2, §4)

      2. Определение положений механизма. ([1], §17; [2], §3.2; [3], Глава 2, §4)

      3. Определение скоростей точек и угловых скоростей звеньев механизма. ([1], §18; [2], §3.2; [3], Глава 2, §4)

      4. Определение ускорений точек и угловых ускорений звеньев механизма. ([1], §18; [2], §3.2; [3], Глава 2, §4)

      5. Кинематический анализ сложных механизмов ([3], Глава 2, §4).



      1. Основная задача и цели кинематического анализа. Методы решения.


    Основная задача кинематики механизмов – изучение движения точек и звеньев механизма без учета сил, действующих на этот механизм.
    Кинематическое исследование механизма преследует три основных цели:


    1. Изучение положений механизма. Изучение перемещений точек и углов поворота звеньев ( ). Определение траекторий движения точек.

    • Результаты исследований по данному пункту используются при определении габаритных размеров механизма, определении формы и размеров внутрикорпусного пространства, определения скоростей, ускорений, решении задач динамического синтеза и анализа.

    1. Определение скоростей точек и угловых скоростей звеньев ( ).

    • Найденные линейные скорости могут быть использованы, в том числе, для определения мощностей сил и приведенной силы; угловые скорости – для определения нормальных ускорений точек, мощностей моментов сил и др. целей.

    1. Определение ускорений точек и угловых ускорений звеньев ( ).

    • Ускорения в задачах динамики позволяют выполнить силовой расчет механизма, т.е. расчет движущей силы и нагруженности кинетических пар по методу кинетостатики (с использованием принципа Даламбера). В кулачковых механизмах по ускорениям судят о динамических нагрузках, возникающих в процессе работы механизма.


    Методы кинематического анализа.


    1. Графический (преимущества - наглядность, прогнозируемость результатов; недостатки - низкая точность, трудоемкость).

    2. Аналитический (высокая точность, но отсутствие наглядности, необходимость дополнительной работы по составлению и отладке программы).

    Аналитическое решение удобно на хорошо отлаженных задачах, требующих исследования выходных параметров механизма при различных вариантах исходных данных или оптимизации этих исходных данных.
    Кинематическому исследованию механизма, как правило, предшествует структурный анализ, в ходе которого определяется степень подвижности механизма и его класс.

    Если механизм имеет степень подвижности, равную единице, то положения, скорости и ускорения точек и звеньев механизма - есть функции положения, скорости и ускорения его начального звена. За начальное звено, обычно, принимают входное звено механизма, а за обобщенную координату – функцию положения этого звена.

    Если механизм имеет второй класс, это значит, что он построен на основе простых диад. В этом случае положения точек и звеньев механизма, их скорости и ускорения определяются обычными методами кинематики.
    Последующие разделы кинематического анализа (см. пп.4.2 - 4.4) изложены в предположении, что механизм имеет степень подвижности, равную единице, и второй класс по классификации Л.В.Ассура.



      1. Определение положений механизма (построение планов положений).


    Построение планов положений является обязательным этапом при решении задачи кинематического анализа графическим методом. Только планы положений позволяют определить траектории отдельных точек механизма. Только с их помощью можно строить планы скоростей и планы ускорений, определять угловые скорости и угловые ускорения звеньев, выполнять динамические расчеты.

    Для лучшего усвоения материала вопрос о построении планов положений рассмотрим системно, выделив исходные данные, цель и порядок решения задачи.

    Постановка задачи:
    Дано:

    1. Кинематическая схема механизма (принципиальная схема, построенная в масштабе).

    2. Положение входного звена или несколько его возможных положений.


    Определить:

    1. Крайние положения механизма.

    2. Положение звеньев механизма при заданных положениях входного звена.


    Порядок решения задачи:


    1. Изображение принадлежащих стойке шарниров, направляющих и т.п.




    1. Определение крайних положений механизма.


    Крайним положением механизма считают такое положение, при котором хотя бы одно звено механизма занимает крайнее положение [4]. При этом под крайним положением звена понимают то его положение, из которого оно может двигаться только в одном направлении. Путь звена, пройденный от одного крайнего положения до другого и измеренный в линейных или угловых единицах измерения, называют ходом звена.

    Крайние положения механизмов, входным звеном которых является кривошип, находят по известным правилам:
    Правило 1: в кривошипно-коромысловом (Рис.4.1) и кривошипно-ползунном механизмах в крайних положениях кривошип ОА и шатун АВ находятся на одной прямой (ОА  СВ).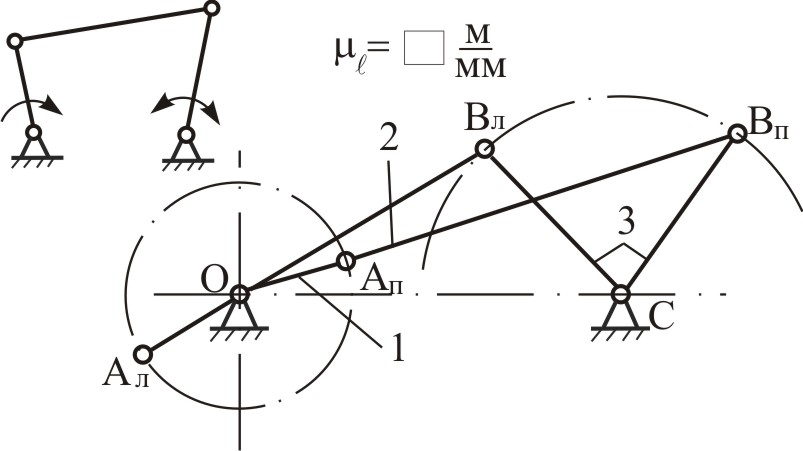




    Используя это правило, покажем алгоритм построений для механизма (Рис.4.1):


    • точки О и С ;

    • окружность r = ОА;

    • окружность R = СВ;

    • дуги ОВл = АВ - ОА;

    ОВп = АВ + ОА

    • точки Вл , Вп , Ал , Ап


    Рис.4.1
    П равило 2: в кривошипно-кулисном механизме (Рис.4.2) в крайних положениях кривошип ОА перпендикулярен кулисе СВ (ОА  СВ).
    Используя это правило, покажем алгоритм построений для механизма (Рис.4.2):


    • точки О и С;

    • окружность r = ОА;

    • касательные из точки С к окружности радиусом r = ОА  т. Ал , т. Ап;

    • ОАл , ОАп - положения кривошипа при крайних положениях кулисы




    1. Выбор «нулевого» (начального) положения (обычно одно из крайних положений, соответствующее началу рабочего хода) и направления движения кривошипа.




    1. Построение промежуточных положений механизма для заданных положений входного звена (кривошипа) методом засечек.

      1. Определение скоростей точек (построение планов скоростей) и угловых скоростей звеньев механизма


    Построение планов скоростей – важнейшая составляющая кинематического анализа.

    Часто на вопрос: « - Зачем строятся планы скоростей?» - студенты вразумительно ответить не могут. Как правило, приходится слышать что-то вроде: «- Для определения величин и направлений скоростей точек». Это понятно. А для чего нужны величины и направления скоростей? Для удовлетворения любопытства? Обычно ответа нет. Отсюда следует, что роль планов скоростей и их значение для задач динамического синтеза и анализа понимается поверхностно.

    Конечно, дело здесь не в любопытстве и не в стремлении нагрузить студента дополнительной малополезной работой. В задачах динамики механизмов кинематической характеристике «скорость» отводится особая роль. При помощи скоростей находят мощности сил сопротивлений и мощности движущих сил, осуществляют приведение сил, выполняют силовые расчеты, энергетические расчеты, расчеты КПД, строят планы ускорений и др. Другими словами, скорости нужны не сами по себе. Они используются, как промежуточный этап и необходимый инструмент решения более сложных задач ТММ.

    Зная это, вопрос определения скоростей следует изучать основательно. Рассмотрим алгоритм построения планов скоростей, начиная с постановки задачи.1
    Постановка задачи:

    Дано:


    1. План положения механизма (кинематическая схема механизма в заданном положении).

    2. Скорость (угловая скорость) входного звена.


    Определить:


    1. Скорости характерных точек механизма (концевые точки звеньев и точки соединения звеньев).2

    2. Скорости любых других точек механизма.

    3. Угловые скорости звеньев.


    Решение.
    Порядок решения задачи проиллюстрируем на примере 2-х простых и одного более сложного механизмов ( см. Примеры 1-3 ):


    • Пример 1 - кривошипно-коромысловый механизм;

    • Пример 2 - кривошипно-ползунный механизм;

    • Пример 3 - кривошипно-ползунный механизм с промежуточной кулисой.


    Построение планов скоростей для сложных механизмов является компиляцией операций, которые выполняются для этих простых.

    Пример 1.







    Рис. 4.3

    Рис. 4.4


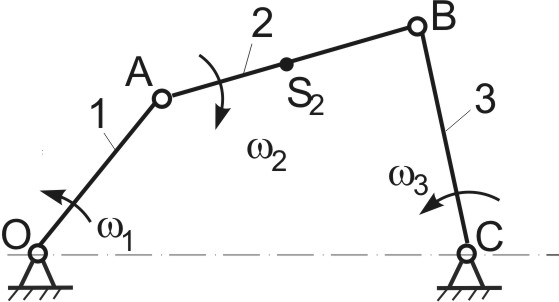
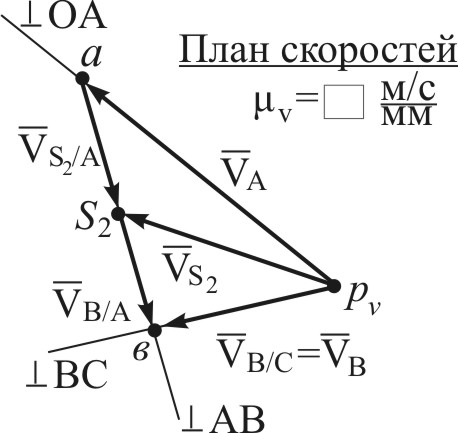
    Дано:

    кривошипно-коромысловый механизм (Рис.4.3) в заданном положении;

    звено 1 – входное; 1 – угловая скорость звена 1; AS2 = 0,5 · AB.
    Определить:

    скорости точек А, В, S2 графическим путем (построением плана скоростей).
    Решение
    Определение скоростей, как и любая другая задача кинематического анализа, выполняется поэтапно, в последовательности, предопределенной формулой строения механизма.

    В нашем случае формула строения имеет вид: I (0,1) → II (2,3).

    Из формулы следует порядок возможных действий:

    - определение и изображение на чертеже скоростей точек первичного механизма;

    - определение и изображение скоростей точек и угловых скоростей звеньев структурной группы II (2,3).

    Следуя этому порядку, первоначально изображают на чертеже скорости характерных точек механизма (концевых точек звеньев и точек подвижных соединений звеньев). Полученный «базовый» план скоростей используют для определения абсолютных значений скоростей самих характерных точек механизма и угловых скоростей звеньев. На втором этапе построений находят и изображают на плане скорости любых других точек.

    Реализуем данный алгоритм для построения плана и определения скоростей точек и звеньев нашего механизма.


    1. Определим и изобразим на плане (Рис.4.4) скорость точки А.


    Точка А является характерной точкой механизма. Она принадлежит звену 1, которое вращается вокруг неподвижного центра О с угловой скоростью .

    Поэтому:

    - величина скорости т. А: (4.1)

    - направление скорости т. А: в направлении .

    Для графических построений выберем масштабный коэффициент плана скоростей:

    (4.2)

    Из (4.2) следует, что скорость на плане будет изображена отрезком длиной . В поле чертежа выберем произвольную точку - полюс плана скоростей. Изобразим вектор = , отложив его от точки перпендикулярно ОА в направлении угловой скорости кривошипа.


    1. Определим и изобразим на чертеже скорость точки В.


    Точка В также является характерной точкой механизма. Это общая точка для звеньев 2 и 3. Для определения скорости точки В следует графически решить систему векторных уравнений: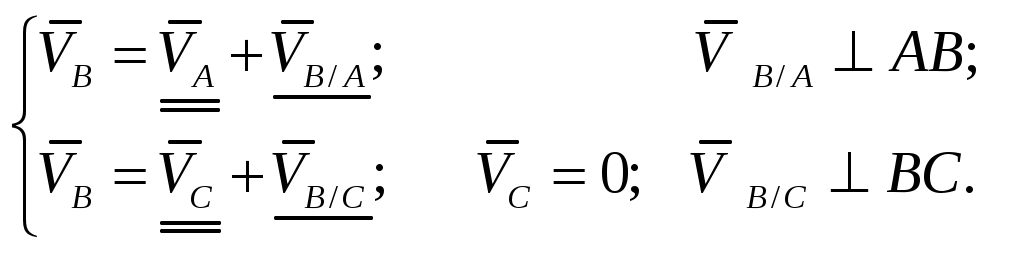
    (4.3)
    В системе (4.3) двумя чертами подчеркнуты векторы, величина и направление которых в данный момент являются известными. Одной чертой подчеркнуты векторы, у которых известно только их направление. Если известные векторы и отложить из одной точки (например, из полюса ) и дорисовать к ним направления и , то задачу по определению неизвестного вектора можно решить графически. Тогда точка будет началом, а точка «в» (полученная на пересечении направлений и ) - концом вектора = , удовлетворяющего одновременно обоим уравнениям системы.

    Таким образом, величины и направления и - также становятся определенными. С учетом , имеем = . Численное значение величины найдем из плана, измерив длину отрезка :


    Базовый план скоростей построен.

    Переходим к определению скоростей других точек. Такой точкой по условию задачи является точка - центр масс звена 2.


    1. Определим скорость точки .

    Скорость т. находим по аналогичной векторной формуле. В этом случае система уравнений не понадобится, т.к. вектор определен ранее, а величина и направление легко определяется (на основании известного ).

    (4.4)

    1. Определим угловые скорости звеньев 2 и 3:

    Угловые скорости и найдем по формулам:

    (4.5)

    Направления и изображаем на рис.4.3 в соответствии с направлениями и на плане скоростей.

    Пример 2.


    Рис.4.5
    Рис. 4.6


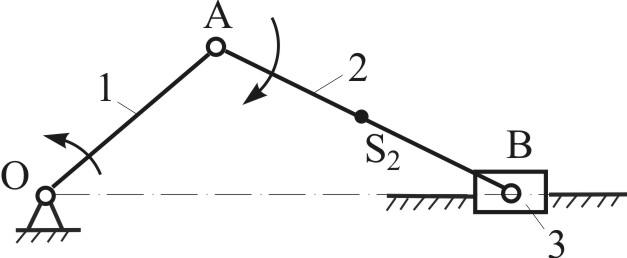
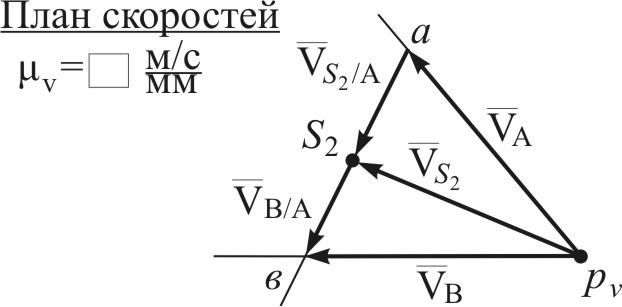
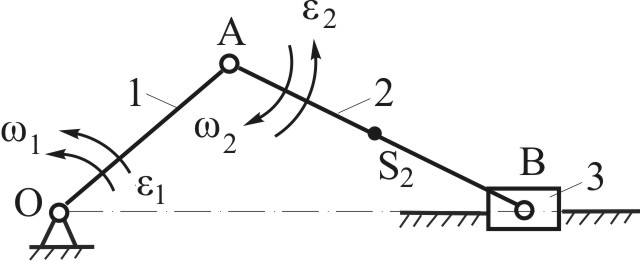
    Дано:

    кривошипно-ползунный механизм (Рис.4.5) в заданном положении;

    звено 1 – входное; 1 - угловая скорость звена 1; AS2 = 0,5 · AB.
    Определить:

    скорости точек А, В, S2 путем построения плана скоростей.
    Решение
    Последовательность и логика построений в данной задаче и в Примере 1 являются аналогичными. Поэтому, решение приводим в конспективном виде.


    1. ;

    2. ;

    3. ; ;

    4. ; ;



    Пример 3.






    Рис. 4.7
    Рис. 4.8


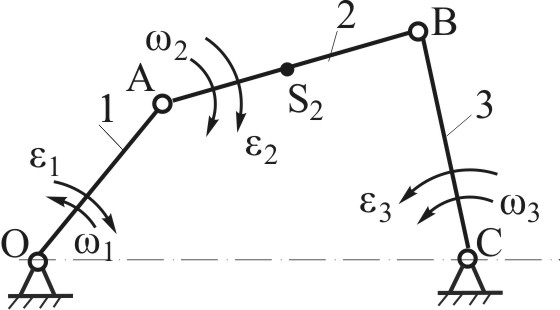
    Дано:

    кривошипно-ползунный механизм с промежуточной кулисой (Рис.4.7) в заданном положении; звено 1 – входное; 1 - угловая скорость звена 1;

    ВS4 = 0,5 · BD.
    Определить:

    скорости точек A, B, D, S4 путем построения плана скоростей.
    Решение.
    Ряд пунктов приведенного ниже алгоритма выполняются аналогично предыдущим примерам и не требуют пояснений. Затруднения могут возникнуть при определении скоростей точек структурной группы (2,3), звенья которой образуют между собой поступательную пару. Построение плана скоростей в этом случае имеет свои особенности, на которые следует обратить внимание (см. пп.2-3 алгоритма).
    При построении планов скоростей кулисных механизмов характерным является использование уравнений, связывающих скорости двух точек, совпадающих в данном положении, но принадлежащих разным звеньям поступательной пары. В нашем примере таким точками будут точки и (Рис.4.7). Точки и совпадают с центром вращательной пары, соединяющей звенья 1 и 2. Поэтому . Точка в данный момент совпадает по положению с точками и , но принадлежит звену 3.

    Рассматривая движение звена 2 как сложное, представим его в виде суммы двух движений: переносного вращательного со звеном 3 и относительного поступательного вдоль звена 3.
    Тогда, для точки звена 2 получим векторное уравнение:

    , (4.6)

    где - абсолютная скорость т. ;

    - переносная скорость т. , в данный момент совпадающая со скоростью т. звена 3;

    - скорость т. при относительном движении звена 2 по звену 3.
    Из (4.6) можно получить уравнение с неизвестным вектором в левой части:

    (4.7)
    Для графического решения уравнения (4.7) из полюса в масштабе откладываем известный вектор (Рис.4.8). Через точку (или совпадающую с ней точку ) конца векторов проводим прямую, направленную параллельно . На этой прямой будет находиться вектор . Одновременно, через полюс проводим прямую, перпендикулярную . На ней будет лежать вектор . Пересечение этих прямых даст точку , определяющую величины векторов и .

    Если скорость т. известна, то легко определить скорость т. , также принадлежащей звену 3, которое вращается вокруг т. (см. п.4 алгоритма).
    Построение плана скоростей для данной задачи можно представить в виде алгоритма действий, приведенного ниже.


    1. ; ; (Рис.4.8);

    2. ; ;

    3. ; ; ;

    4. ;

    5. ; ;

    6. , ;

    7. ; ; ; ; .




      1. Определение ускорений точек (построение планов ускорений) и угловых ускорений звеньев механизма


    Как и планы скоростей, планы ускорений, как правило, строят не ради самих ускорений, а с целью дальнейшего их использования.

    Одно из возможных направлений этого использования - силовой анализ механизма. Если силовой расчет выполняется по методу кинетостатики, ускорения необходимы для определения фиктивных сил инерции (сил инерции Даламбера). Таким образом, определение ускорений (как и определение скоростей) - не самоцель. Обычно, это промежуточный этап решения более сложной задачи.

    Рассмотрим построение планов ускорений на примерах 2-х простых механизмов.
    Постановка задачи

    Дано:

    1. План механизма в заданном положении.

    2. Угловая скорость и угловое ускорение ведущего звена.

    3. Угловые скорости всех других звеньев механизма.


    Определить:

    1. Ускорения характерных точек (точки соединения звеньев).

    2. Ускорения других точек.

    3. Угловые ускорения звеньев.


    Пример 1. – кривошипно-коромысловый механизм (Рис.4.9)



    Рис. 4.9

    Рис. 4.10


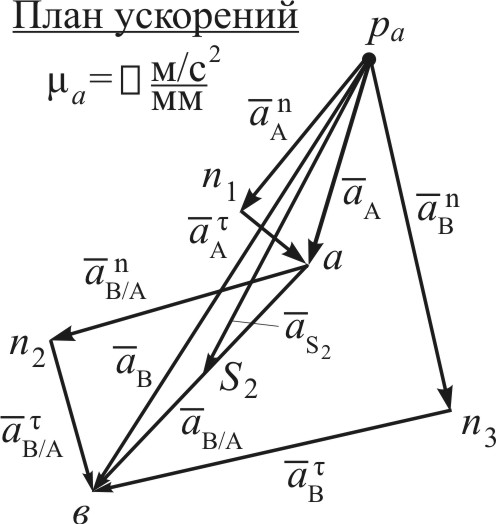
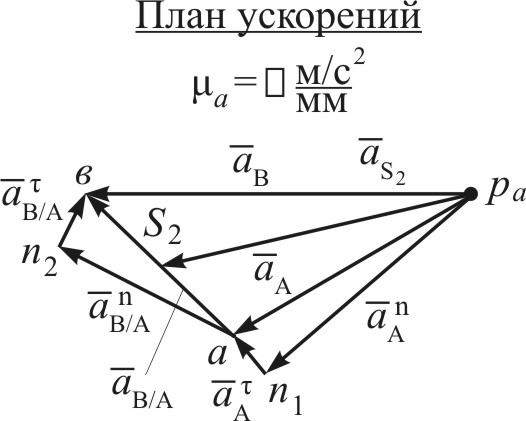
    Решение



    1. Определим ускорение точки А

    (4.8)

    (4.9)

    Направления: (Рис.4.10)


    1. Выберем масштабный коэффициент плана ускорений и построим вектор :

    (4.10)

    ; ; ;

    1. Определим ускорение точки 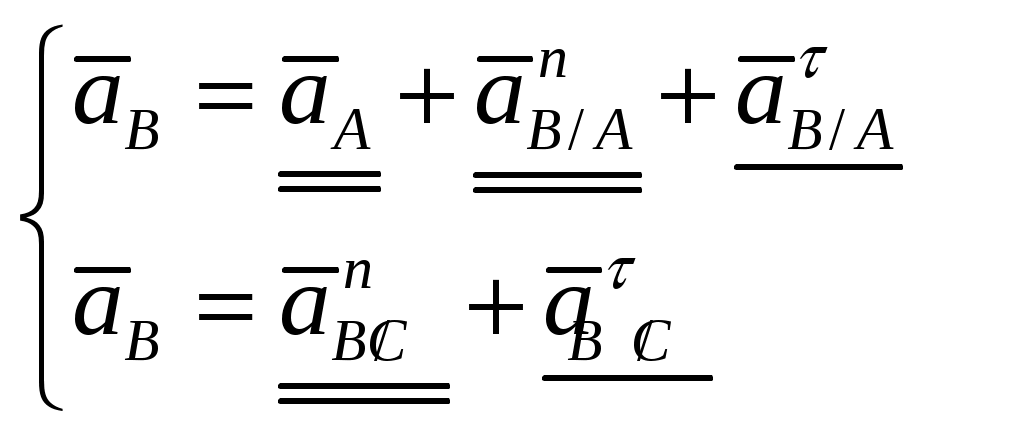(точка принадлежит 2-м звеньям)


    (4.11)
    ; ; (4.12)


    1. Определим значения абсолютных и относительных ускорений точек

    и т.д. (4.13)

    1. Определим угловые ускорения звеньев

    (4.14)

    Направления и показываем соответственно направлениям и .
    Пример 2. – кривошипно-ползунный механизм (Рис.4.11)


    Рис. 4.11
    Рис. 4.12


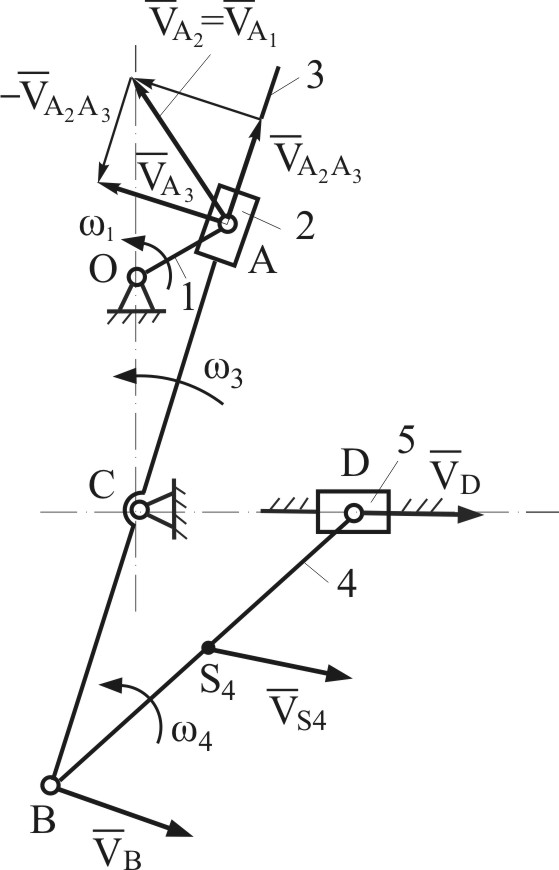
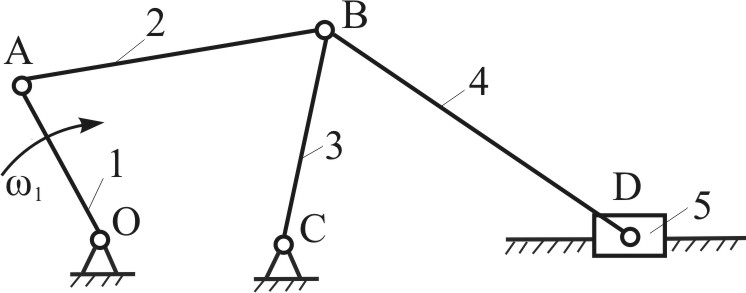
    Алгоритм построений (Рис.4.12)


    1. ;

    2. ; = … ;

    3. ; ;

    4. , .

      1. Кинематический анализ сложных механизмов


    Кинематический анализ сложных механизмов выполняется в последовательности, определяемой формулой строения механизма, т.е.:

    1. Анализ механизма I класса.

    2. Анализ группы Ассура, следующей за механизмом I класса.

    3. Анализ последующих групп Ассура.


    В качестве примера рассмотрим механизм, изображенный на рис.4.13.

    Формула строения этого механизма: I(0,1) II(2,3)  II(4,5)




    Рис. 4.13

    Решение.


    1. Определение кинематических характеристик звена 1: положение, угловая скорость, угловое ускорение (если не заданы) и кинематических характеристик точки А .



    1. Определение кинематических характеристик точек и звеньев группы Ассура II(2,3) – положение, .

    2. Определение кинематических характеристик точек и звеньев группы Ассура II(4,5) – положение, .


    Таким образом, задача по определению кинематических характеристик для механизма (рис.4.13) сводится к последовательному решению задач для кривошипно-коромыслового, а затем коромыслово-ползунного механизмов (которые рассмотрены ранее в примерах).
    З адание для самостоятельной работы и самоконтроля усвоения материала:
    Дано: На рис.4.14 показана кинематическая схема эллипсографа - прибора для построения правильных эллипсов. Геометрические размеры таковы, что .

    Требуется: Доказать, что точки, принадлежащие шатуну эллипсографа двигаются по эллиптическим траекториям. Задачу решить графическим методом. Результаты сравнить с данными аналитического решения.

    Аналитическое решение


    1. W = 3n-2p5-p4= 33–24 = 1




    (1 зв. + 2 к/пары – “лишние”, т.к. не влияют на

    движение механизма)


    1. Определим координаты произвольной точки М (Рис.4.15), а затем, исключив параметр , найдем уравнение траектории движения этой точки:




    (r + BM) = A1 = const

    (r - BM) = A2 = const
    (4.15)
    Уравнение (4.15) – уравнение эллипса.
    Замечание. В лекции не рассмотрено построение плана ускорений для кулисного механизма. Желающим разобраться в этом вопросе рекомендуем обратиться к учебнику [3], Глава 2, §4.
    Вопросы для самоконтроля


      1. Назовите задачу и цели кинематического исследования механизмов.

      2. Каким основным признаком руководствуются при построении крайних положений четырехзвенных кривошипно-коромыслового или кривошипно-ползунного механизмов?

      3. Какое положение занимает кривошип по отношению к кулисе в крайних положениях кривошипно-кулисного механизма?

      4. Объясните общий порядок построения планов скоростей и ускорений для рычажных механизмов II класса.

      5. Масштабные коэффициенты планов скоростей и ускорений. Какова их размерность? Как вычисляются значения масштабных коэффициентов?

      6. Нарисуйте звено АВ длиной . Покажите на рисунке заданные параметры ., указав их направления произвольно. Напишите векторные формулы для определения скорости и ускорения точки В. Определите и . путем схематических графических построений.

      7. Изучив разделы 4.3 и 4.4 лекции 4, постройте схематический план скоростей (показать только направления векторов) и схематический план ускорений для механизма, изображенного на рис.4.13.

    Лекция 5

    1   2   3   4   5   6   7   8   9

    написать администратору сайта