Лекции ОХТ для заочников. Лекция 1 Предмет и содержание курса охт
 Скачать 1.88 Mb.
|
Распределение времени пребывания в проточных реакторахГоворя о времени пребывания реагентов в реакторе, мы имеем в виду некоторую среднюю величину. Исключение составляет лишь модель РИВ, в которой все частицы пребывают в реакторе одинаковое время. Для РИС и реальных реакторов, описываемых диффузионными и ячеечной моделями, время пребывания отдельных частиц в реакторе может быть разным. Это время зависит от траектории, которую описывает каждая частица потока в своем движении от входа к выходу. Чем сложнее эта траектория, тем большим оказывается время пребывания. В свою очередь, траектория движения частицы зависит от гидродинамики потоков (неравномерности распределения скоростей и давлений, турбулентности, внутренних течений, вызванных градиентами концентраций, температур, поверхностного натяжения и др.). Таким образом, очевидно, что для РИС и реальных реакторов время пребывания является случайной величиной и может быть описано только с помощью вычислительного аппарата математической статистики. Непрерывная случайная величина может быть задана с помощью функций распределения случайной величины. Различают интегральную функцию распределения F(τ) и дифференциальную функцию распределения или плотность распределения f(τ). Интегральная функция распределения – это объемная доля потока, выходящего из реактора, которая находилась в нем в течении времени, меньшим, чем τ. Свойства этой функции: при τ2 > τ1 F(τ2) ≥ F(τ1) F(0) = 0 F(∞) = 1 Производная от этой функции  называется плотностью распределения. Среднее время пребывания частицы в реакторе при использовании функций распределения можно рассматривать как математическое ожидание непрерывной случайной величины.Экспериментально функции распределения времени пребывания могут быть найдены путем исследования так называемых кривых отклика. Суть этого метода состоит в следующем. На входе в реактор создается некоторое возмущение. Таким возмущением является введение в основной поток вещества (индикатора), отличающегося по какому-либо свойству: окраске, электропроводности, оптической плотности, кислотности, радиоактивности и т.д.). Индикатором может быть вещество, которое не изменяется и не поглощается в ходе эксперимента; концентрация его должна легко контролироваться. Возмущение на входе (входной сигнал) может быть ступенчатым или импульсным. 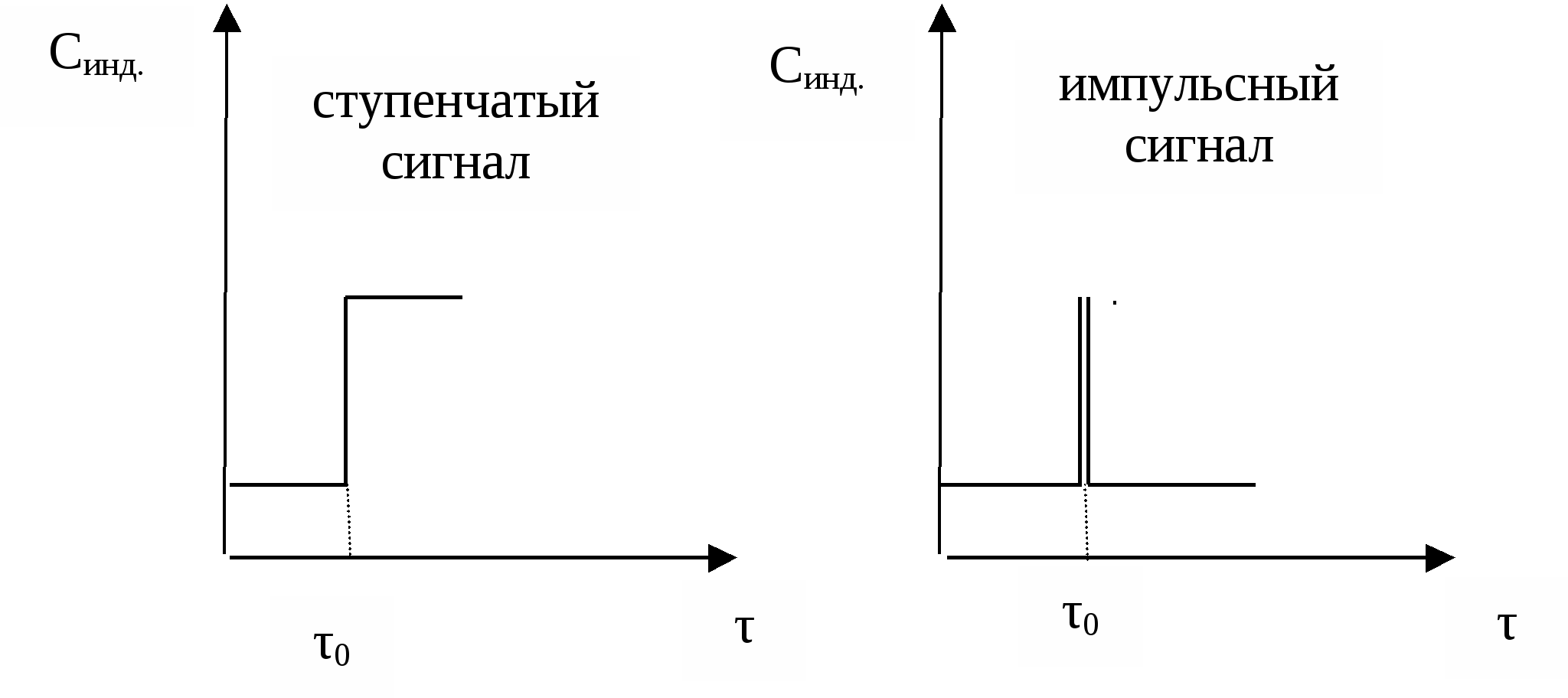 Для получения кривой отклика на входной сигнал (выходного сигнала) измеряют в разные моменты времени концентрацию индикатора в потоке, выходящим из реактора. Синд. = f(τ) Выходной сигнал при ступенчатом входном сигнале используют для определения интегральной функции распределения F(τ); дифференциальная функция распределения f(τ) соответствует кривой отклика на сигнал импульсной формы. 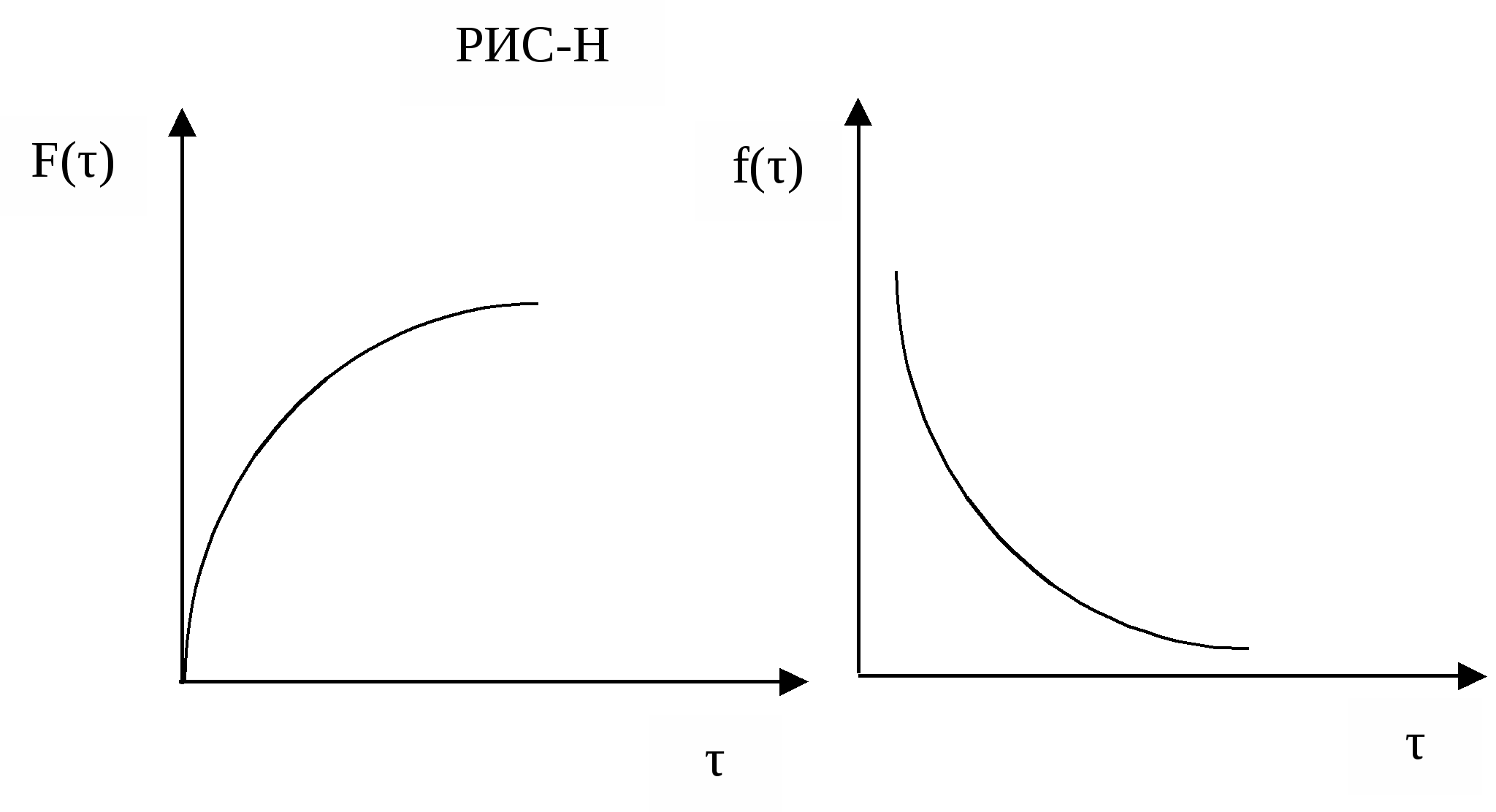 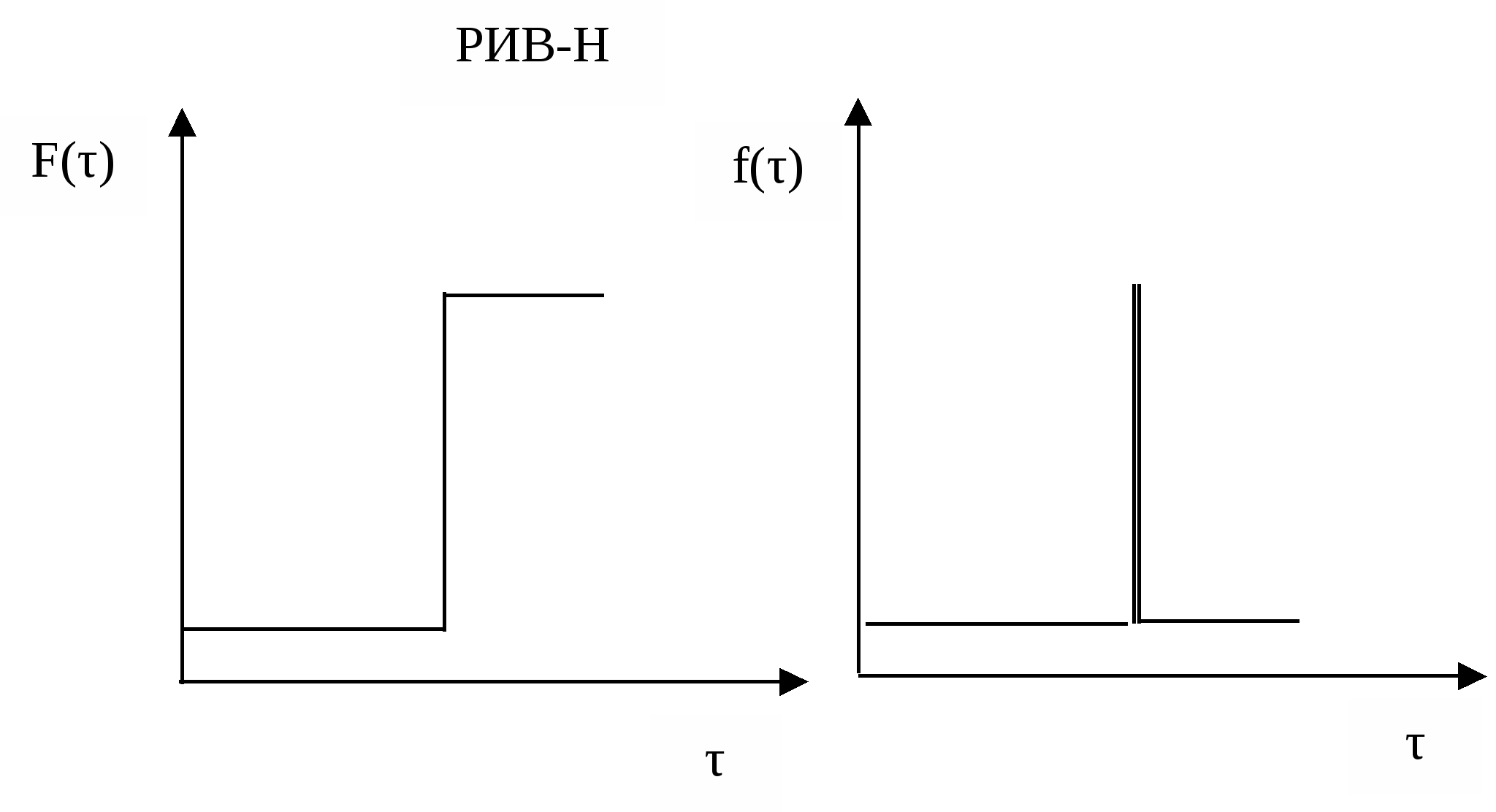 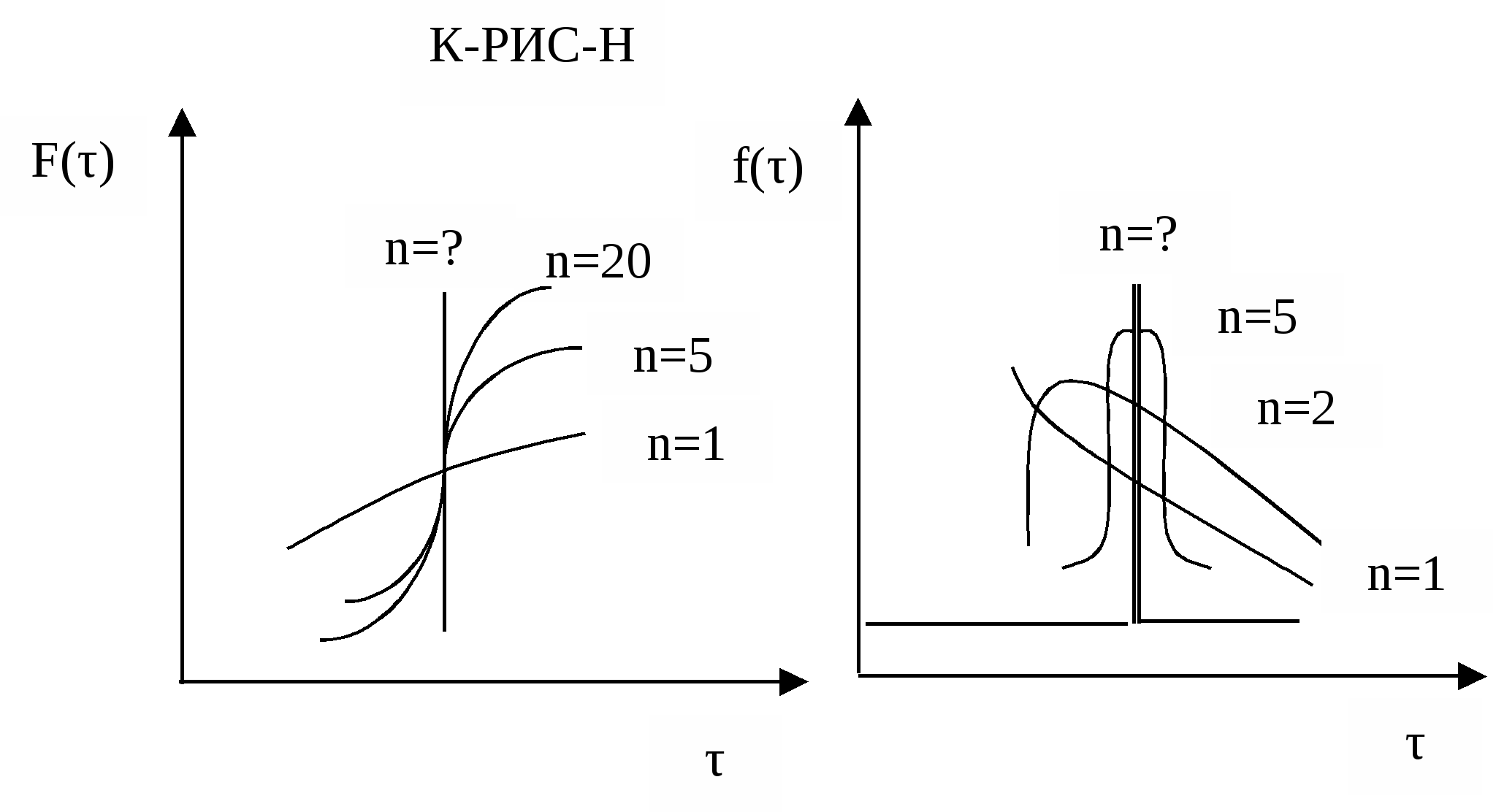 Сравним кривые отклика для идеального и реального реактора вытеснения. 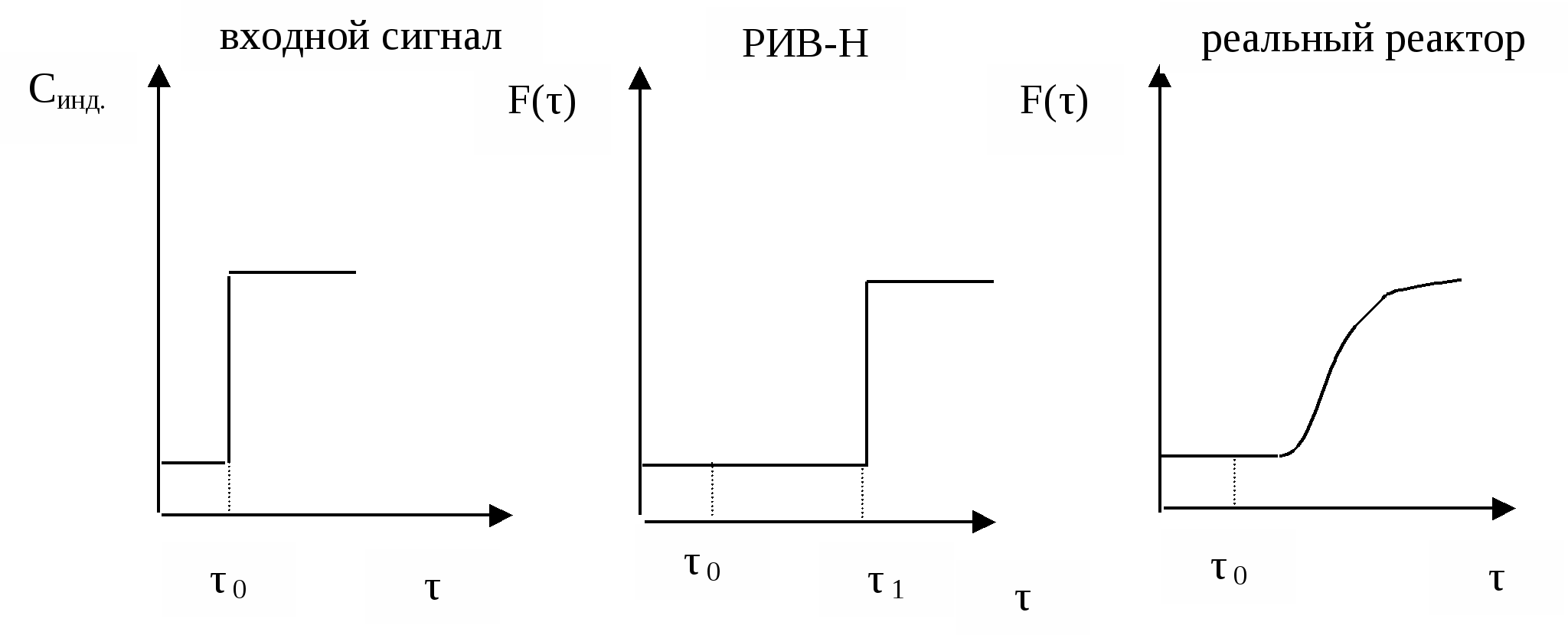 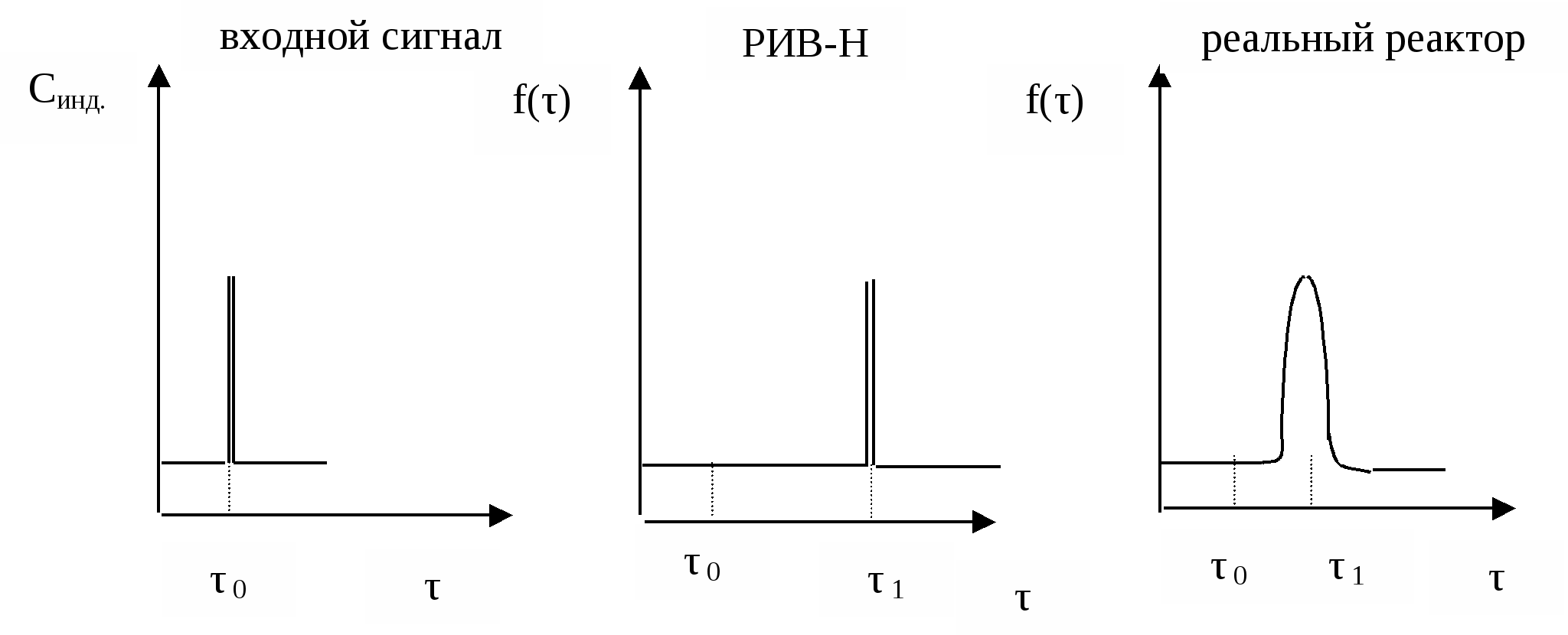 На основе функций распределения можно рассчитать среднее время пребывания частиц реагентов в проточном реакторе, определить тип модели. Учесть отклонение от этой модели и т.д. Лекция № 14 Теплоперенос в химических реакторах Температура оказывает существенное влияние на скорость химического процесса и другие показатели его эффективности. При проведении реакций разного типа требуется различный температурный режим. Под температурным режимом реактора понимают поддержание в нем необходимой и оптимальной для данного процесса температуры. В промышленной практике используют два типа температурного режима:
Выбор режима определяется, в основном, технологическим классом реакции.
Температура в реакторе может изменяться по двум причинам:
По тепловому режиму выделяют три модели реакторов: адиабатический, изотермический и политропический. Учет всех тепловых явлений осуществляется при составлении теплового баланса реактора, уравнение которого, наряду с уравнением материального баланса, является основой для расчета реакторов. Уравнение теплового баланса реактора В общем виде уравнение теплового баланса записывается Qприход = Qрасход, где Qприход – количество тепла, поступающего в реактор в единицу времени, Qрасход – количество тепла, расходуемого в реакторе в единицу времени. Тепло приходит в реактор с реагентами Qреаг. и выделяется (или поглощается) в результате химической реакции Qхим.р. Qприход = Qреаг. ± Qхим.р. Расход тепла происходит в результате уноса тепла с продуктами Qпрод., теплообмена с окружающей средой Qт/об.; часть тепла накапливается в реакторе Qнакоп.. Qрасход = Qпрод. ± Qт/об. + Qнакоп. Qреаг. ± Qхим.р.= Qпрод. ± Qт/об. + Qнакоп. Обозначим Qпрод.- Qреаг. = Qконв. – конвективный перенос тепла. Тогда после преобразований получим Qнакоп. = - Qконв. ± Qт/об. ± Qхим.р. - уравнение теплового баланса реактора в общем виде. Если температура неодинакова в разных точках объема реактора или во времени, используют дифференциальную форму уравнения теплового баланса, выведенную для некоторого элементарного объема dx dy dz. 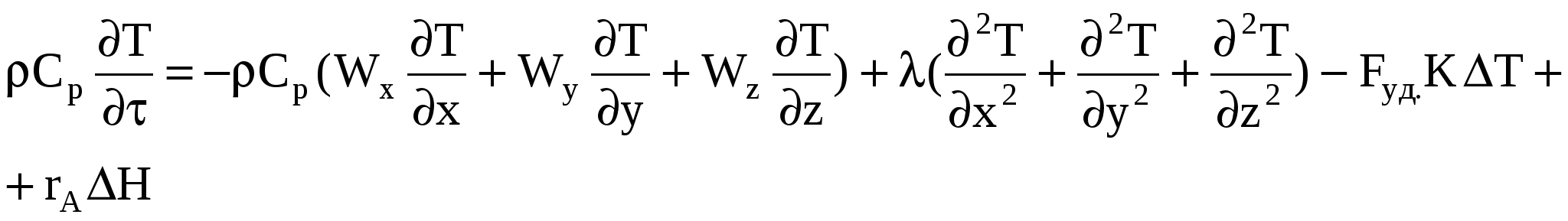 где ρ – плотность реакционной смеси; Ср – удельная теплоемкость реакционной смеси; x,y,z – пространственные координаты, Wx, Wy, Wz - составляющие скорости движения потока в направлении осей x,y,z; λ – коэффициент молекулярной и турбулентной теплопроводности реакционной смеси; Fуд. – удельная поверхность теплообмена; К – коэффициент теплопередачи; ∆Т = Т – Тт/нос. ( Т – температура реакционной смеси, Тт/нос. – температура теплоносителя); rA - скорость химической реакции; ∆Н – тепловой эффект реакции. Решение дифференциального уравнения связано с большими трудностями. Однако в каждом конкретном случае его можно упростить. Например, при стационарном режиме в проточных реакторах Qнакоп. = 0, для периодических реакторов отсутствует конвективный перенос тепла Qконв. = 0. Выведем уравнения теплового баланса для различных гидродинамических и тепловых моделей реакторов. 1.Политропический режим а)РИС-П В периодическом реакторе нет конвективного переноса тепла, то есть  Тогда уравнение теплового баланса приобретает вид  Проведем некоторые преобразования.  CA = CA0 (1-αA)  После подстановки получим  Умножив уравнение на dτ и разделив на СА0, получим  Обозначим  - мольная теплоемкость реакционной смеси. , где Vp –объем реактора, F–общая поверхность теплообмена.СА0 Vp = NA0 – мольный расход реагента А (количество кмоль реагента А, загруженного в реактор). Тогда  В результате проведенных преобразований получаем уравнение теплового баланса РИС-П в политропическом режиме в следующем виде  б) РИВ-Н Тепловые процессы в РИВ-Н описываются дифференциальной формой теплового баланса при условии, что в реакторе не происходит накопление тепла (стационарный режим), а конвективный перенос тепла происходит исключительно по длине реактора. 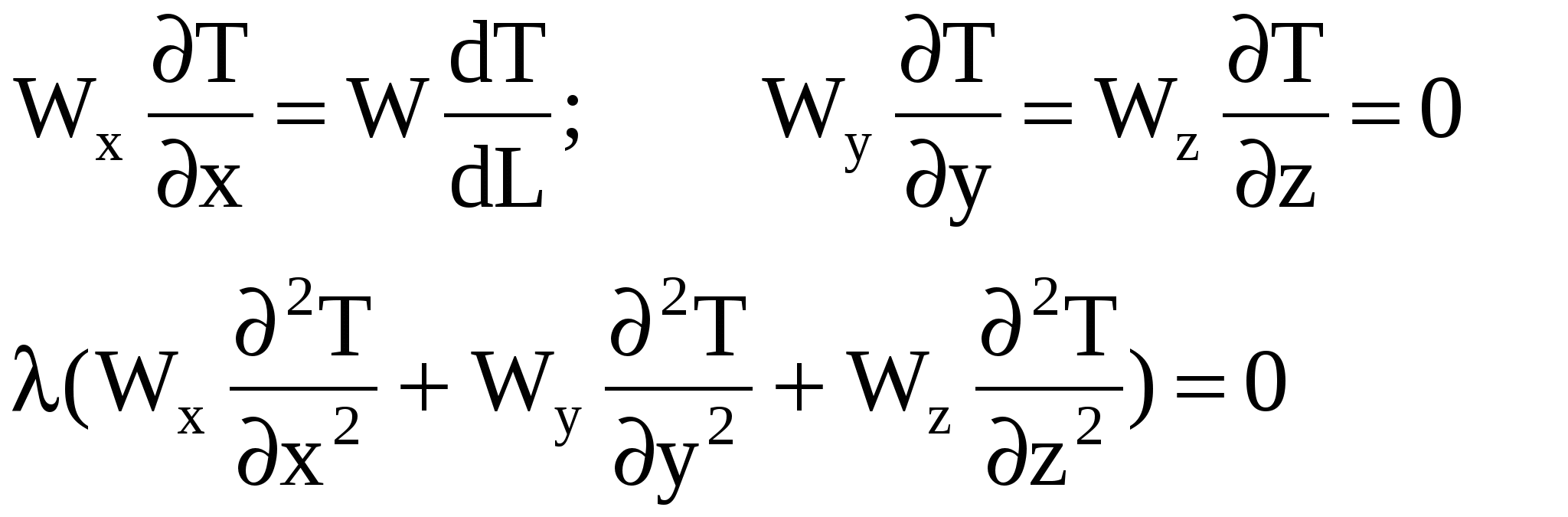 При таких условиях уравнение теплового баланса имеет вид   Ранее было выведено, что  . Тогда Разделим уравнение на СА0 и умножим на dτ.  , где  .Проведем некоторые преобразования:  ,где  - поверхность теплообмена, приходящаяся на 1 м длины реактора, dL – длина элемента реактора,  - мольный расход реагента (мольная скорость, моль/час).Итак, уравнение теплового баланса РИВ-Н в политропическом режиме имеет вид  в)РИС-Н Этот реактор работает в стационарном режиме, для него характерно отсутствие градиента параметров как во времени, так и по объему реактора. Поэтому уравнение теплового баланса, так же как и уравнение материального баланса, составляют сразу для всего реактора в целом. Qнакопл. = -Qконвек. – Qт/об. + Qхим.р. Qнакопл. = 0, Qхим.р = Qконвек. + Qт/об. Qхим.р = rA ΔH Vp =  , т.к. Vp = υоб.τ.Qконвек. = ρ Ср υоб. (Т – Т0), где Т0 – температура на входе в реактор. Qт/об. = F K ΔT. Тогда ρ Ср υоб. (Т – Т0) + F K ΔT = СА0 αА ΔH υоб.. Разделим уравнение на СА0 υоб. = ВА0. Получим уравнение теплового баланса РИС-Н в политропическом режиме  2. Адиабатический режим Qт/об. = 0 РИС-П Ср* dT = H d(A) РИВ-Н Ср* dT = H d(A) РИС-Н Ср* (T – Т0) = H A 3.Изотермический режим T = const, T = T0 РИВ-Н  РИС-Н   В адиабатическом режиме для РИС-Н Ср* (T – Т0) = H A. Отсюда Т – Т0 =  .Обозначим  - адиабатическая разность температур.Тогда Т = Т0 Тад.А Знак - соответствует эндотермической реакции, знак + - экзотермической реакции. Такую же зависимость можно вывести для РИВ-Н в адиабатическом режиме. Ср* dT = H d(A) 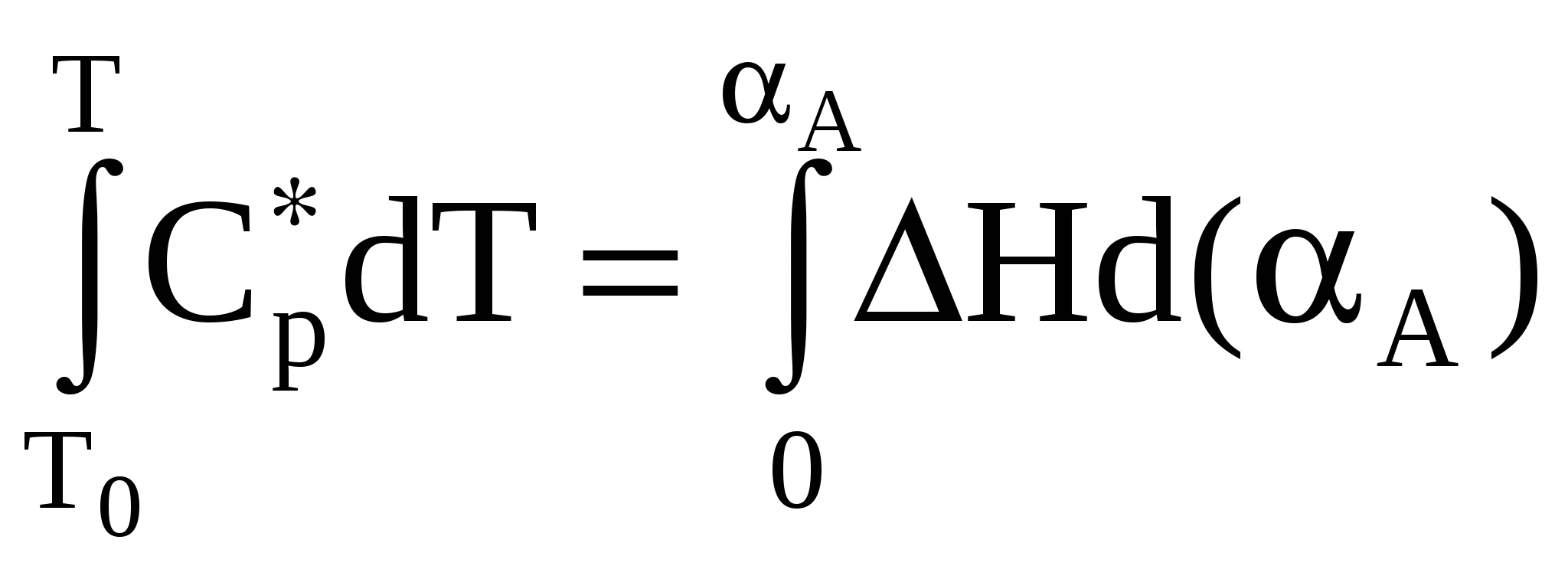 Пусть Ср* и H не зависят от температуры, тогда Ср* (T – Т0) = H A. Т = Т0 Тад.А. Это уравнение показывает, что между степенью превращения реагента и изменением температуры существует линейная зависимость. Поэтому в адиабатическом реакторе в любой момент времени (для определенной величины конверсии) можно рассчитать температуру реакционной смеси. |