|
|
Физика. Лекции. Лекция1 Предмет механики
Угловая скорость
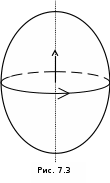 Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени.
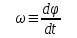 ,. (7.1) ,. (7.1)
Псевдовектор  направлен по оси вращения так же, как и псевдовектор направлен по оси вращения так же, как и псевдовектор  (рис. 7.3). (рис. 7.3).
Радиан – единица измерения угла – величина безразмерная (см. на рис. 3.2), поэтому из (7.1) следует, что угловая скорость измеряется в рад/с или в с-1.
Угловое ускорение
Угловым ускорением 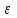 называется векторная величина, равная первой производной угловой скорости по времени или второй производной угла поворота по времени. называется векторная величина, равная первой производной угловой скорости по времени или второй производной угла поворота по времени.
 . (7.2) . (7.2)
Из (7.2) следует, что размерность углового ускорения  . Из определения (7.2) следует, что угловое ускорение является псевдовектором. . Из определения (7.2) следует, что угловое ускорение является псевдовектором.
В случае закрепленной оси вращения направление углового ускорения совпадает с направлением угловой скорости при ускоренном движении и противоположно при замедленном.
§ 4. Связь угловых и линейных кинематических величин
 . .
Формула (7.3) выражает связь между модулями линейной и угловой скорости: линейная скорость равна угловой, умноженной на радиус окружности, по которой движется материальная точка.
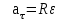 . .
 . .
§ 5. Работа при вращательном движении. Момент силы
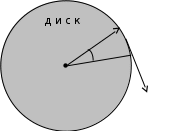
Рис. 8.1
На рис. 8.1 приведен самый простой пример вращения твердого тела при действии внешней силы. Тело представляет собою диск, который может вращаться вокруг неподвижной оси Z, проходящей через его центр перпендикулярно рисунку. Внешняя сила направлена по касательной к диску (такую силу можно создать с помощью нити, намотанной на диск).
.
Величина Мz называется моментом силы F относительно оси вращения Z.

§ 6. Кинетическая энергия при вращательном движении.
Момент инерции
Кинетическую энергию вращающегося тела можно найти как сумму кинетических энергий всех материальных точек, составляющих данное тело. Скорости этих точек 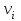 связаны с угловой скоростью и расстояниями от точек до оси вращения. Воспользовавшись этим, мы можем выразить кинетическую энергию вращающегося тела через его угловую скорость: связаны с угловой скоростью и расстояниями от точек до оси вращения. Воспользовавшись этим, мы можем выразить кинетическую энергию вращающегося тела через его угловую скорость:
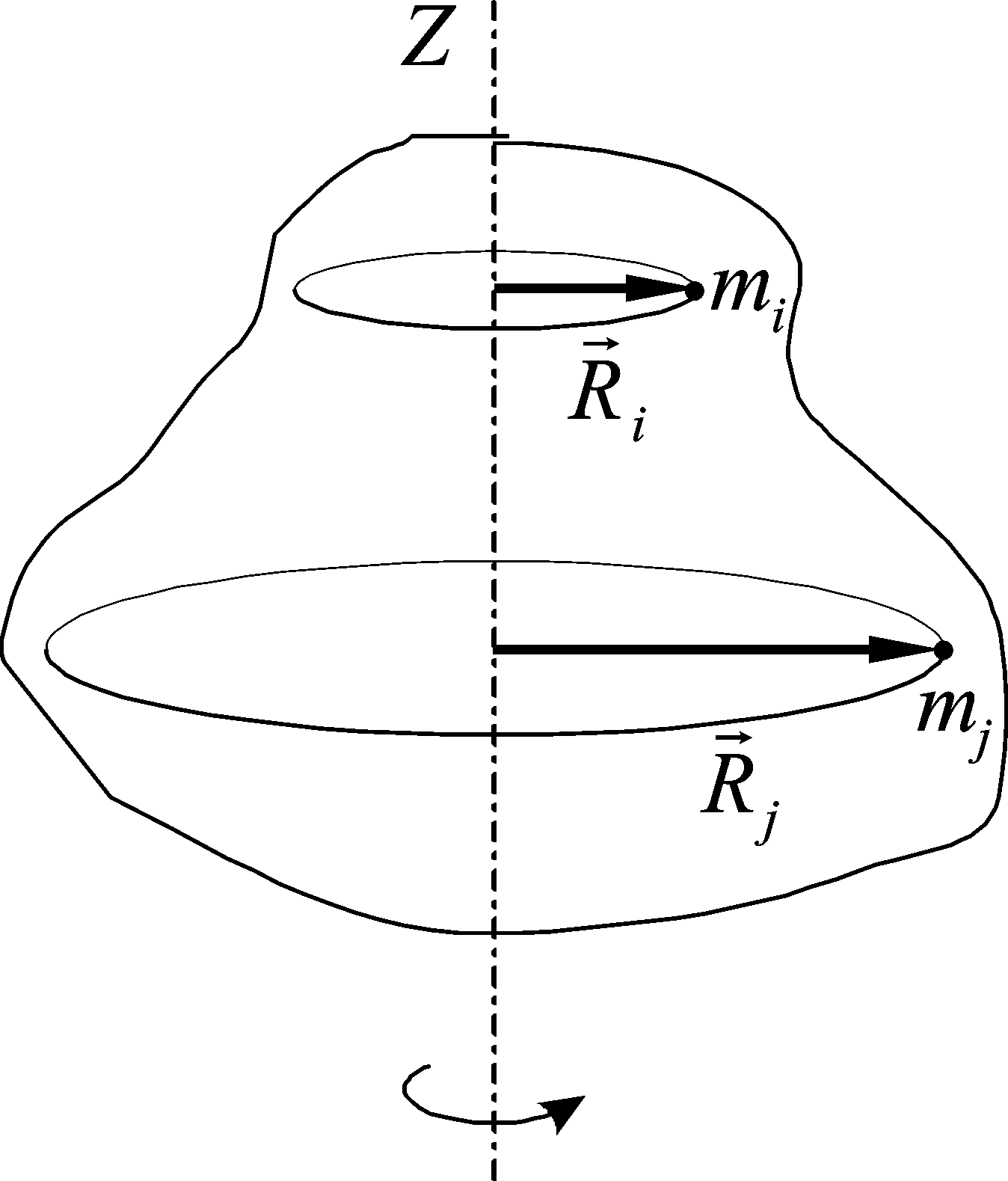  . .
Рис. 8.3
Введем новую величину 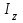 , являющуюся мерой инертности при вращательном движении: , являющуюся мерой инертности при вращательном движении:
 . (8.5) . (8.5)
Величина 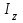 называется моментом инерции твердого тела, относительно оси Z. называется моментом инерции твердого тела, относительно оси Z.
Таким образом:
 . (8.6) . (8.6)
Величину, стоящую под знаком суммы в формуле (8.6) называют моментом инерции материальной точки относительно оси z:
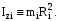 (8.7) (8.7)
Следовательно, момент инерции материальной точки равен произведению массы этой точки на квадрат ее расстояния до оси вращения.
Таким образом, момент инерции твердого тела равен сумме моментов инерции всех материальных точек, составляющих это тело:
 (8.8) (8.8)
Как видно из формулы (8.5), величина момента инерции материальной точки  может быть разной для материальных точек с одинаковыми массами может быть разной для материальных точек с одинаковыми массами  вследствие возможного различия расстояний вследствие возможного различия расстояний 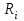 от этих точек до оси вращения. от этих точек до оси вращения.
Теорема Штейнера
Для симметричных тел вычисления по формуле (8.11) значительно упрощаются, если ось вращения проходит через центр масс тела. Обозначим момент инерции твердого тела относительно оси ОО, проходящей через центр масс, через  (рис. 8.4). Тогда для нахождения момента инерции относительно произвольной оси (рис. 8.4). Тогда для нахождения момента инерции относительно произвольной оси  , параллельной оси ОО и удаленной от нее на расстояние а, можно воспользоваться теоремой Штейнера, которую иллюстрирует рис. 8.2. , параллельной оси ОО и удаленной от нее на расстояние а, можно воспользоваться теоремой Штейнера, которую иллюстрирует рис. 8.2.
В соответствии с рис. 8.2, теорему Штейнера запишем следующей формулой:
 , (8.12) , (8.12)
где I0 – момент инерции относительно оси OО;
I – момент инерции относительно оси OО;
а – расстояние между осями.

Рис. 8.4
Ниже приведем моменты инерции I0 для некоторых тел.
Обруч  , где R – радиус обруча , где R – радиус обруча
Диск:  , где R – радиус диска. , где R – радиус диска.
Шар:  , где R – радиус шара. , где R – радиус шара.
Стержень:  , где l– длина стержня; m – масса рассматриваемых тел. , где l– длина стержня; m – масса рассматриваемых тел.
§ 1. Уравнение динамики вращательного движения
Основное уравнение динамики вращательного движения:
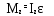 . (9.2) . (9.2)
§ 2. Момент импульса
Запишем основной закон динамики вращательного движения в форме (9.1), а затем занесем момент инерции  под знак производной по времени: под знак производной по времени:
 , или , или 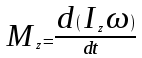 . (9.3) . (9.3)
Введем понятие момента импульса  абсолютно твердого тела относительно оси вращения Z следующим определением: абсолютно твердого тела относительно оси вращения Z следующим определением:
 . (9.4) . (9.4)
Следовательно
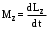 . (9.6) . (9.6)
Это еще одна форма уравнения динамики вращательного движения тела вокруг неподвижной оси.
Понятие момента импульса используется не только для описания вращения твердых тел, но и для более общего случая движения произвольной системы материальных точек. В этом случае моментом импульса системы материальных точек называется векторная сумма моментов импульса материальных точек, входящих в систему.
Момент импульса материальной точки относительно произвольной точки О пространства определяется как векторное произведение радиус-вектора материальной точки, проведенного из точки О, на вектор импульса этой материальной точки.
Опираясь на второй закон Ньютона, можно показать, что закон изменения со временем момента импульса системы имеет следующий вид:
 , (9.9) , (9.9)
здесь M – суммарный момент внешних сил.
При сделанных выше оговорках относительно осей вращения, закон изменения момента импульса применим и для описания вращения твердых тел.
§ 3. Закон сохранения момента импульса
Закон сохранения момента импульса, который формулируется так: момент импульса системы материальных точек остается постоянным, если суммарный момент внешних сил равен нулю.
ЛЕКЦИЯ № 4
Постулаты специальной теории относительности.
Преобразования Лоренца
Классическая механика, т.е. механика, в основе которой лежат законы Ньютона, правильно описывает движения тел при условии, что их скорости малы по сравнению со скоростью света в вакууме  . Эта ограниченность классической механики стала ясной в конце XIX века в связи с развитием электродинамики – раздела физики, изучающего свойства и взаимодействие движущихся электрических зарядов, изучение и распространение электромагнитных полей. В начале XX века трудами Г.А. Лоренца, А. Пуанкаре, А. Эйнштейна, М. Планка, Г. Минковского была создана механика, область применимости которой не ограничивалась только малыми скоростями – релятивистская механика (от латинского relativus – относительный). . Эта ограниченность классической механики стала ясной в конце XIX века в связи с развитием электродинамики – раздела физики, изучающего свойства и взаимодействие движущихся электрических зарядов, изучение и распространение электромагнитных полей. В начале XX века трудами Г.А. Лоренца, А. Пуанкаре, А. Эйнштейна, М. Планка, Г. Минковского была создана механика, область применимости которой не ограничивалась только малыми скоростями – релятивистская механика (от латинского relativus – относительный).
Как выяснилось, скорости движения любых материальных объектов не могут превышать скорости света в вакууме. Релятивистская механика правильно описывает движение тел при любых скоростях, в том числе и при скоростях, сравнимых со скоростью света. При малых скоростях, v << c, формулы релятивистской механики переходят в формулы механики Ньютона. Релятивистская механика основана на теории относительности, рассматривающей пространственно-временные закономерности для любых физических процессов. Наиболее общая теория пространства-времени называется общей теорией относительности (ОТО). Она создана в 1915 году А. Эйнштейном. Согласно ОТО, свойства пространства-времени в данной области определяются действующими в ней полями тяготения. Изучение ОТО лежит за рамками курса общей физики.
§ 1. Преобразования Галилея.
|
|
|
 Скачать 1.62 Mb.
Скачать 1.62 Mb. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени.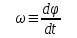 ,. (7.1)
,. (7.1) направлен по оси вращения так же, как и псевдовектор
направлен по оси вращения так же, как и псевдовектор  (рис. 7.3).
(рис. 7.3). 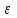 называется векторная величина, равная первой производной угловой скорости по времени или второй производной угла поворота по времени.
называется векторная величина, равная первой производной угловой скорости по времени или второй производной угла поворота по времени. . (7.2)
. (7.2) . Из определения (7.2) следует, что угловое ускорение является псевдовектором.
. Из определения (7.2) следует, что угловое ускорение является псевдовектором. .
.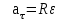 .
. .
.


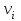 связаны с угловой скоростью и расстояниями от точек до оси вращения. Воспользовавшись этим, мы можем выразить кинетическую энергию вращающегося тела через его угловую скорость:
связаны с угловой скоростью и расстояниями от точек до оси вращения. Воспользовавшись этим, мы можем выразить кинетическую энергию вращающегося тела через его угловую скорость:
 .
.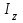 , являющуюся мерой инертности при вращательном движении:
, являющуюся мерой инертности при вращательном движении: . (8.5)
. (8.5) . (8.6)
. (8.6)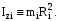 (8.7)
(8.7) (8.8)
(8.8) может быть разной для материальных точек с одинаковыми массами
может быть разной для материальных точек с одинаковыми массами  вследствие возможного различия расстояний
вследствие возможного различия расстояний 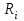 от этих точек до оси вращения.
от этих точек до оси вращения.  (рис. 8.4). Тогда для нахождения момента инерции относительно произвольной оси
(рис. 8.4). Тогда для нахождения момента инерции относительно произвольной оси  , параллельной оси ОО и удаленной от нее на расстояние а, можно воспользоваться теоремой Штейнера, которую иллюстрирует рис. 8.2.
, параллельной оси ОО и удаленной от нее на расстояние а, можно воспользоваться теоремой Штейнера, которую иллюстрирует рис. 8.2. , (8.12)
, (8.12)
 , где R – радиус обруча
, где R – радиус обруча , где R – радиус диска.
, где R – радиус диска.  , где R – радиус шара.
, где R – радиус шара.  , где l– длина стержня; m –
, где l– длина стержня; m – 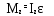 . (9.2)
. (9.2) под знак производной по времени:
под знак производной по времени: , или
, или 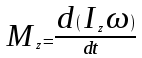 . (9.3)
. (9.3) абсолютно твердого тела относительно оси вращения Z следующим определением:
абсолютно твердого тела относительно оси вращения Z следующим определением: . (9.4)
. (9.4)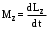 . (9.6)
. (9.6) , (9.9)
, (9.9) . Эта ограниченность классической механики стала ясной в конце XIX века в связи с развитием электродинамики – раздела физики, изучающего свойства и взаимодействие движущихся электрических зарядов, изучение и распространение электромагнитных полей. В начале XX века трудами Г.А. Лоренца, А. Пуанкаре, А. Эйнштейна, М. Планка, Г. Минковского была создана механика, область применимости которой не ограничивалась только малыми скоростями – релятивистская механика (от латинского relativus – относительный).
. Эта ограниченность классической механики стала ясной в конце XIX века в связи с развитием электродинамики – раздела физики, изучающего свойства и взаимодействие движущихся электрических зарядов, изучение и распространение электромагнитных полей. В начале XX века трудами Г.А. Лоренца, А. Пуанкаре, А. Эйнштейна, М. Планка, Г. Минковского была создана механика, область применимости которой не ограничивалась только малыми скоростями – релятивистская механика (от латинского relativus – относительный).