Физика. Лекции. Лекция1 Предмет механики
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
Принцип относительности ГалилеяПреобразования Галилея – это уравнения, связывающее координаты и время некоторого СОБЫТИЯ в двух инерциальных системах отсчета. СОБЫТИЕ определяется местом, где оно произошло (координаты x, y, z), и моментом времени t, когда произошло событие. Событие полностью определено, если заданы четыре числа: x, y, z, t – координаты события. Полученные четыре формулы и есть преобразования Галилея: 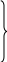 x = x' + Vt, x = x' + Vt,y = y', z = z', t = t'. § 2. Постулаты СТО. Преобразования Лоренца Специальная теория относительности (СТО), базируется на двух исходных утверждениях, постулатах: I. Принцип относительности, согласно которому никакими физическими опытами нельзя установить, покоится ли данная система отсчета, либо движется равномерно и прямолинейно. Другая формулировка: Все законы природы одинаково формулируются для всех инерциальных систем отсчета. II. Принцип постоянства скорости света:cкорость света в вакууме во всех инерциальных системах отсчета одинакова и не зависит ни от движения источника, ни от движения приемника света. Преобразования Лоренца – это уравнения, связывающие координаты и время некоторого события в двух инерциальных системах отсчета. В отличие от преобразований Галилея, преобразования Лоренца не должны противоречить постулатам СТО: необнаружимости абсолютного движения и постоянству скорости света. При скорости движения системы отсчета V << с преобразования Лоренца должны переходить в преобразования Галилея. Такие преобразования были найдены в 1904 году голландским физиком Г.А. Лоренцом и имеют следующий вид:
Здесь буквой для удобства записи обозначена следующая величина: 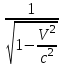 . (11.5) . (11.5)Релятивистская механика должна быть построена таким образом, чтобы уравнения движения не менялись при переходе из одной инерциальной системы отсчета в другую, т.е. были инвариантны относительно преобразований Лоренца. ЛЕКЦИЯ № 1 § 1. Исторический обзор. Закон сохранения заряда 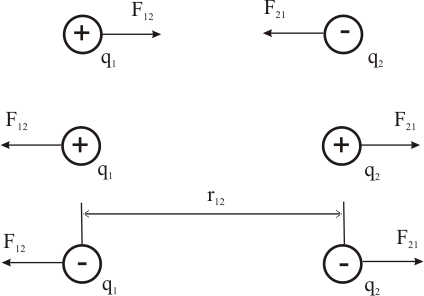 Заряды разных знаков притягиваются друг к другу, заряды одного знака отталкиваются.  Рис. 1.1 Рис. 1.1 Электрический заряд Величина элементарного заряда в системе СИ: е = 1,6021892 10-19 Кл. Любой заряд содержит целое число элементарных зарядов: 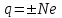 , ,Можно сформулировать закон сохранения заряда: суммарный заряд электрически изолированной системы не изменяется. § 2. Закон КулонаВзаимодействие точечных зарядов в воздухе экспериментально изучал в 80-е годы XVIII в. французский физик Шарль Кулон. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других заряженных тел. Точечный заряд – модельное понятие (см. ч. I, лекция 1). Кулон установил, что сила взаимодействия точечных зарядов пропорциональна величине взаимодействующих зарядов и обратно пропорциональна квадрату расстояния между ними, т.е.: 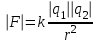 , (1.1) , (1.1)где 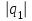 и и 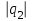 – модули величин взаимодействующих зарядов; – модули величин взаимодействующих зарядов; r – расстояние между ними; k – коэффициент пропорциональности, который следует определить из опыта. Сила – вектор, поэтому нужно определить не только модуль силы (формула (1.1)), но и ее направление. Направление вектора можно задать с помощью единичного вектора. Единичный вектор – это вектор, модуль которого равен единице. Система единиц измерения Опытным путем установлено, что заряды в 1 Кл на расстоянии 1 м в вакууме взаимодействуют с силой 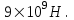 Подставляя значения заряда, расстояния и силы в формулу (1.1) для коэффициента k, получаем значение:  . (1.3) . (1.3)Принято для удобства вместо коэффициента k использовать выражение: 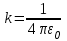 , ,где 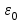 – электрическая постоянная, значение ее, как следует из (1.3), равно: – электрическая постоянная, значение ее, как следует из (1.3), равно: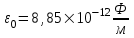 (фарад на метр), (1.3а) (фарад на метр), (1.3а)Фарада – единица электрической емкости (см. лекцию 5). Размерность 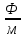 равна равна  . .§ 3. Электрическое поле Согласно современным представлениям, взаимодействие покоящихся электрических зарядов на расстоянии осуществляется через электрическое поле. Каждый электрический заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляет себя в том, что создает силу, действующую на каждый электрический заряд, помещенный в электрическое поле. Напряженность электрического поля 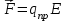 , (1.5) , (1.5)Где E – напряженность электрического поля точечного заряда в вакууме. В общем случае, для электрического поля, создаваемого произвольным распределением зарядов, напряженностью электрического поля называют, по определению, векторную величину, равную отношению силы, действующей на пробный заряд 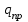 , к величине пробного заряда: , к величине пробного заряда:  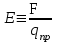 (1.7) (1.7)Единица напряженности в системе СИ имеет название вольт на метр (В/м). При такой напряженности на заряд 1 Кл действует сила в 1 Н. Графическое изображение электрических полей Чтобы получить наглядное представление об электрическом поле, его можно изобразить с помощью линий напряженности электрического поля (их называют также силовыми линиями). Линия напряженности – это линия, касательная к которой в каждой точке совпадает с направлением напряженности электрического поля в данной точке. Линии напряженности выходят из положительного заряда и уходят в бесконечность, либо заканчиваются на отрицательном заряде. В том месте, где модуль напряженности поля больше, линии проводят гуще, меньше – реже, так, что густота линий пропорциональна модулю напряженности. На рис. 1.5а, 1.5б показаны силовые линии для точечного положительного и отрицательного зарядов, на рис. 1.5г показана картина поля для 2-х равных по величине одноименных зарядов, на рис. 1.5в – для 2-х равных по величине разноименных зарядов.   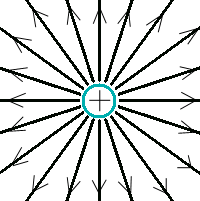 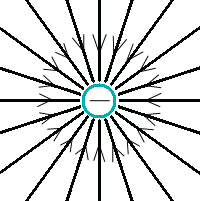 а) поле положительного заряда б) поле отрицательного заряда  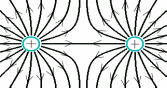 в) поле двух разноименных зарядов г) поле двух одноименных зарядов   § 4. Поток вектора напряженности электрического поля Допустим, что в каждой точке пространства определено значение напряженности электрического поля. Выберем в пространстве элемент площади 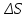 , площадка должна быть настолько малой, чтобы в пределах ее вектор можно было считать постоянным. Ориентация площадки определяется вектором единичной нормали к ней, единичная нормаль – это перпендикуляр к площадке. , площадка должна быть настолько малой, чтобы в пределах ее вектор можно было считать постоянным. Ориентация площадки определяется вектором единичной нормали к ней, единичная нормаль – это перпендикуляр к площадке.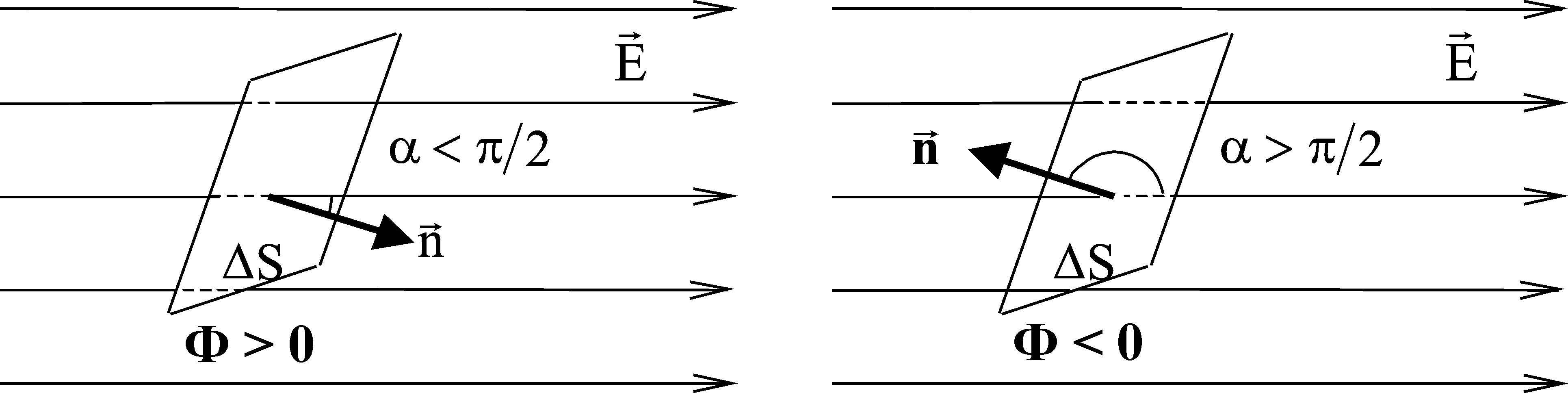   , (2.1) , (2.1)В пределе, когда площадь элемента выбирается все меньше, а число элементов N стремится к бесконечности, выражение для потока переходит в интеграл: 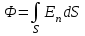 . (2.2) . (2.2)§ 5. Теорема Гаусса Можно сформулировать следующую теорему, известную как теорема Гаусса: поток вектора напряженности электрического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри поверхности, деленной на 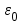 – электрическую постоянную: – электрическую постоянную: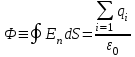 . (2.3) . (2.3)§ 6. Применение теоремы Гаусса для расчета электрических полей Поле бесконечной равномерно заряженной плоскости Если заряд распределен в тонком поверхностном слое заряженного тела, то его можно охарактеризовать поверхностной плотностью заряда. Поверхностная плотность заряда – это заряд, приходящийся на единицу площади поверхности: 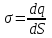 . .Единица измерения: 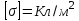 ; (2.4) ; (2.4)Напряженность электрического поля, создаваемого бесконечной заряженной плоскостью, по модулю равна:  . (2.5) . (2.5)Напомним, что направлен вектор 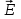 перпендикулярно заряженной плоскости. перпендикулярно заряженной плоскости.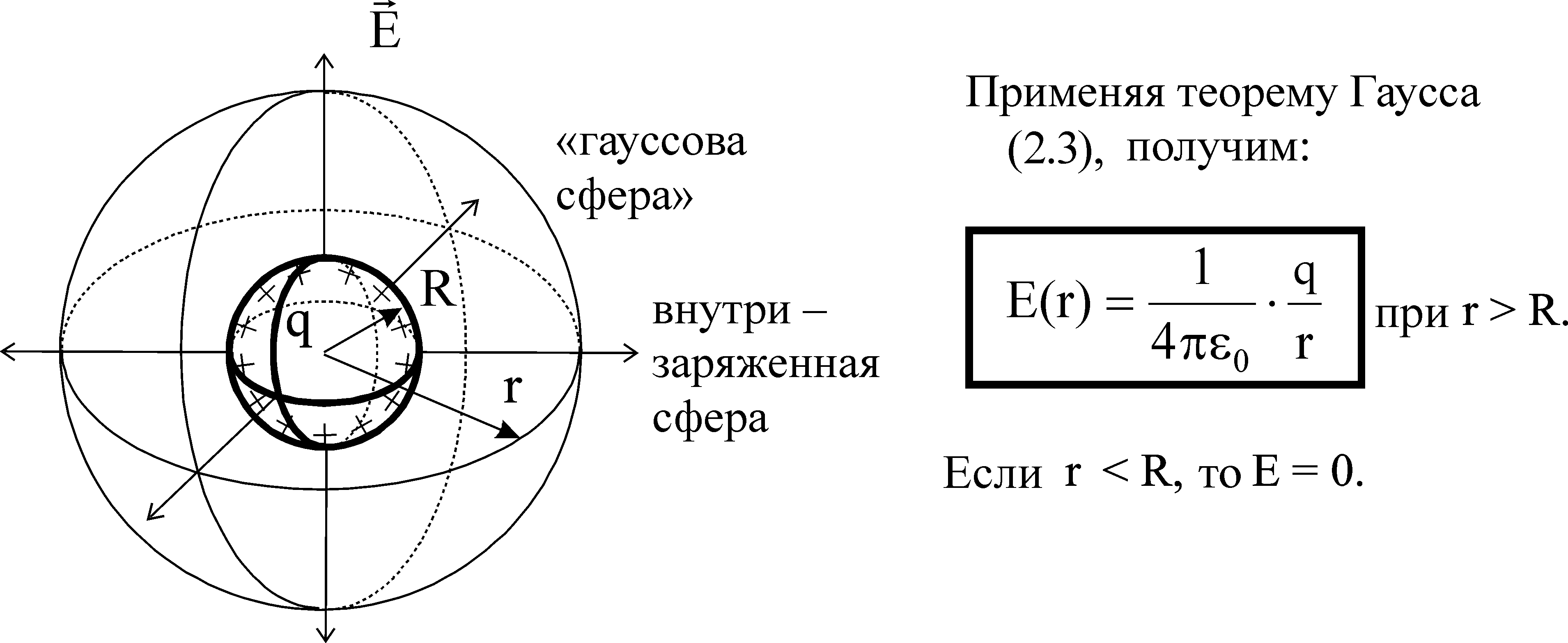 Рис. 2.5 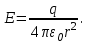 (2.7) (2.7)Таким образом, для точек вне или на сферической поверхности электрическое поле равномерно заряженной сферы такое же, как у точечного заряда, находящегося в центре сферы, величина которого равна суммарному заряду сферической поверхности. Внутри сферы поле равно нулю.  Объемную плотность заряда можно выразить через полный заряд шара: 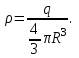 Окончательно для поля внутри шара получаем: 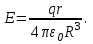 (2.9) (2.9)Напряженность электрического поля бесконечной равномерно заряженной нити Линейная плотность заряда определяется следующим образом: 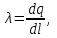 [] = Кл/м. [] = Кл/м. Выражение для напряженности поля можно получить, построив «гауссову поверхность» вокруг заряженной нити (см. рис. 2.7). Вывод предоставляется читателю, приводим окончательный результат: 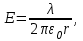 при r R. (2.10) при r R. (2.10)§ 1. Работа сил электростатического поля в случае двух точечных зарядов   . (3.1) . (3.1)§ 2. Потенциал  (3.2) (3.2)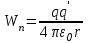 . (3.3) . (3.3)Из формулы (3.3) видно, что потенциальную энергию взаимодействия двух точечных зарядов можно представить как произведение величины второго заряда 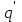 на функцию , зависящую от величины первого заряда q и расстояния до точки, в которой находится второй заряд: на функцию , зависящую от величины первого заряда q и расстояния до точки, в которой находится второй заряд:  где 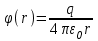 – потенциал электростатического поля точечного заряда (3.4) – потенциал электростатического поля точечного заряда (3.4)В общем случае электростатический потенциал поля, создаваемого произвольным распределением зарядов равен, по определению, отношению потенциальной энергии 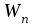 пробного заряда пробного заряда  в электростатическом поле к величине этого пробного заряда: в электростатическом поле к величине этого пробного заряда: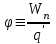 . (3.5) . (3.5)Единица потенциала в системе СИ – вольт (В): 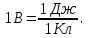 Следовательно, работу электростатического поля по перемещению электрического заряда можно выразить, используя (3.2) и (3.6), следующим образом: 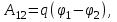 (3.7) (3.7)здесь  – потенциалы поля в точках, между которыми переместился заряд. – потенциалы поля в точках, между которыми переместился заряд.§ 3. Циркуляция вектора напряженности электрического поля Из формулы (3.7) следует, что при перемещении заряда в электрическом поле по замкнутой траектории работа, совершаемая силами поля, равна нулю. В Если траектория замкнута, то из (3.13) и (3.7) следует, что: 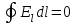 , (3.14) , (3.14)кружок у знака интеграла в (3.14) обозначает, что интеграл берется по замкнутому контуру. Интеграл вида (3.14) по замкнутому контуру называют циркуляцией вектора 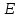 . Следовательно, циркуляция вектора . Следовательно, циркуляция вектора 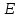 электростатического поля, вычисленная по любому замкнутому контуру, равна нулю. Это общее свойство всех полей консервативных сил (потенциальных полей). электростатического поля, вычисленная по любому замкнутому контуру, равна нулю. Это общее свойство всех полей консервативных сил (потенциальных полей).Эквипотенциальные поверхности, их связь с силовыми линиямиДля наглядного изображения электрического поля можно, наряду с линиями напряженности, силовыми линиями, использовать эквипотенциальные поверхности. Из самого названия следует, что эквипотенциальные (лат. аequus – равный) поверхности – это поверхности равного потенциала. Следовательно, уравнение эквипотенциальной поверхности имеет вид:  Форма эквипотенциальных поверхностей связана с формой силовых линий: эквипотенциальные поверхности расположены так, что в каждой точке пространства силовая линия и эквипотенциальная поверхность взаимно перпендикулярны. ЛЕКЦИЯ № 2 § 1. Проводники и диэлектрики Проводники – это вещества, в которых есть свободные электрические заряды. Концентрация свободных зарядов в металлических проводниках того же порядка, что и концентрация атомов. Эти заряды могут перемещаться в пределах проводника, если в нем создано электрическое поле. Диэлектрики – это вещества, в которых почти нет свободных электрических зарядов. Полупроводники по концентрации свободных зарядов занимают промежуточное положение между проводниками и диэлектриками. У них концентрация свободных зарядов очень сильно зависит от температуры. § 2. Заряженный проводник Если проводник зарядить, то свободные заряды в нем придут в движение и двигаться они будут до тех пор, пока напряженность электрического поля в проводнике не станет равной нулю, так как сила, действующая на заряд. Т.е. равны нулю все производные потенциала, следовательно, внутри заряженного проводника потенциал постоянен, т.е. объем проводника и его поверхность – эквипотенциальны. Согласно теореме Гаусса из этого следует, что объемная плотность заряда внутри проводника равна нулю. Весь заряд проводника распределен по его поверхности. Напряженность электрического поля вне проводника перпендикулярна его поверхности, так как она эквипотенциальна 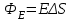 , ,на основании теоремы Гаусса: 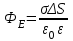 , ,следовательно, напряженность электрического поля вблизи поверхности проводника: 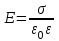 . (5.1) . (5.1)§ 3. Проводник во внешнем электрическом поле Если внести проводник в область, где существует электрическое поле, то в начальный момент времени поле в проводнике существует. Под действием силы, действующей на заряды в электрическом поле, свободные заряды придут в движение и будут перемещаться, пока напряженность электрического поля не станет равной нулю. В результате движения зарядов в противоположных концах проводника возникают поверхностные заряды противоположного знака, которые называют индуцированными зарядами (см. рис. 5.1а, 5.1б, 5.1в): Рис. 5.1а 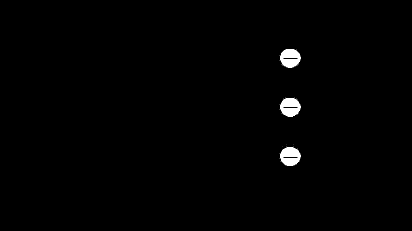 Электроны под действием силы F начинают двигаться против поля. Рис. 5.1б  Перераспределившиеся заряды создают поле Перераспределившиеся заряды создают поле 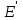 , направленное навстречу , направленное навстречу 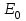 . Когда величина . Когда величина 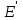 сравняется с сравняется с 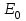 , тогда результирующее поле в проводнике: , тогда результирующее поле в проводнике: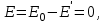 перераспределение  Рис. 5.1вэлектронов закончится.Поле индуцированных зарядов накладывается на стороннее поле и приводит к его изменению, в итоге: 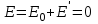 внутри проводника. Вне проводника напряженность электрического поля вблизи его поверхности перпендикулярна поверхности, так как поверхность проводника – эквипотенциальная. § 4. Электроемкость, конденсаторы Как мы установили, потенциал заряженного проводящего тела постоянен во всех точках тела. Потенциал пропорционален заряду. Справедливость этого утверждения для всех тел произвольной формы была проверена расчетами и экспериментом. Таким образом, можно утверждать, что: 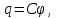 (5.2) (5.2)где q – заряд тела; – его потенциал. Коэффициент пропорциональности между потенциалом и зарядом называется электроемкостью или просто емкостью уединенного проводника: 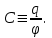 (5.3) (5.3)Единица измерения емкости – это емкость тела, у которого при заряде в 1 Кл потенциал равен 1 В. Единица измерения емкости имеет свое наименование – «фарад» 1 Ф = 1 Кл В. В технике широко используются специальные устройства, которые накапливают (конденсируют) заметные по величине заряды при относительно небольших потенциалах. Такие устройства называются конденсаторами. Заряды на обкладках конденсатора имеют одинаковую величину q и противоположны по знаку. Проводники, образующие конденсатор, называют обкладками. Основной характеристикой конденсатора является его емкость, которая определяется из соотношения: 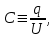 (5.4) (5.4)где  – разность потенциалов или напряжение между обкладками конденсатора; q – заряд конденсатора. – разность потенциалов или напряжение между обкладками конденсатора; q – заряд конденсатора.Емкость плоского конденсатора Наиболее распространенный тип конденсатора – это плоский конденсатор: две близко расположенные разноименно заряженные пластины, между которыми находится диэлектрик . 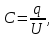 (5.4а) (5.4а)заряд  , где S – площадь пластины. , где S – площадь пластины.Напряжение U, согласно (3.20), равно:  где d – расстояние между обкладками, следовательно, емкость плоского конденсатора равна:  (5.5) (5.5)Из выражения (5.5) видно, что емкость конденсатора пропорциональна площади обкладок и относительной диэлектрической проницаемости диэлектрика и обратно пропорциональна расстоянию между обкладками. Емкость сферического конденсатора . Сферический конденсатор – это две концентрические проводящие сферы (рис. 5.3), разделенные диэлектриком. 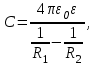 (5.6) (5.6)Емкость цилиндрического конденсатора равна:  (5.7) (5.7)здесь l – длина конденсатора;  – радиусы обкладок. – радиусы обкладок.Энергия и плотность энергии электрического поля Введем понятие плотности энергии электрического поля w в соответствии со следующим определением: 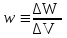 , (5.12) , (5.12)где W – энергия электрического поля, запасенная в объеме V.  С учетом (5.11) из (5.12) для плотности энергии электрического поля в вакууме получим: 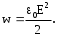 Если пространство, где создано электрическое поле напряженностью Е, заполнено диэлектриком, то в соответствии с выводом (4.7) из лекции 4, 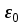 следует заменить на следует заменить на 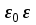 , тогда, для плотности энергии электрического поля в диэлектрике, имеем: , тогда, для плотности энергии электрического поля в диэлектрике, имеем: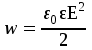 . (5.13) . (5.13)Если поле  неоднородно, то тогда, зная плотность энергии поля в каждой точке, можно следующим образом найти энергию поля, заключенную в любом объеме V: неоднородно, то тогда, зная плотность энергии поля в каждой точке, можно следующим образом найти энергию поля, заключенную в любом объеме V: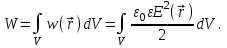 (5.14) (5.14)Энергия заряженного конденсатораЭнергию W заряженного конденсатора найдем, умножив w из (5.13) на объем конденсатора V = Sd. Выразив, в соответствии с (3.22), напряженность электрического поля Е через разность потенциалов (напряжение) U, получим:  С учетом формулы емкости плоского конденсатора (5.5) для энергии заряженного до напряжения U конденсатора емкостью С имеем следующее выражение: 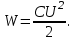 (5.15) (5.15)Формула (5.15) верна для конденсаторов любой формы, хотя получили мы ее для частного случая плоского конденсатора. ЛЕКЦИЯ № 3 § 1. Сила тока, плотность тока 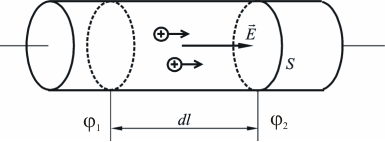 Рис. 6.1 Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. Если направленное движение происходит под действием электрического поля, ток называют током проводимости, если упорядоченное движение – это движение зарядов под действием механического перемещения макроскопического тела, то ток называется конвекционным. Количественной характеристикой электрического тока служит сила тока. Если через поперечное сечение проводника за время dt проходит заряд dq, то по определению сила тока: 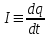 . (6.1) . (6.1)Сила тока – скалярная величина, определяемая электрическим зарядом, проходящим через поперечное сечение в единицу времени. За направление тока условно принимается направление перемещения положительныхзарядов. Единица силы тока – «ампер» (А); единицы силы тока и заряда связаны соотношением: 1 Кл = 1 А·с. (6.1а) Если сила тока и его направление не меняются во времени, то такой ток называют постоянным, если меняется, то ток называют переменным. Плотность тока Ток может протекать через проводник большого сечения, при этом величина заряда, переносимого через отдельные участки сечения, может меняться. Более того, может меняться и направление движения зарядов (см. рис. 6.2).  В связи с этим вводится понятие плотности тока. В связи с этим вводится понятие плотности тока. Выделим в проводнике площадку 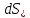 , перпендикулярную направлению движения зарядов в этой точке проводника. Пусть сила тока, протекающего через эту площадку равна , перпендикулярную направлению движения зарядов в этой точке проводника. Пусть сила тока, протекающего через эту площадку равна  . Плотность тока по определению равна: . Плотность тока по определению равна: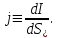 (6.2) (6.2)Плотность тока характеризуется не только своей величиной j, но и направлением движения зарядов. Плотность тока – это векторная физическая величина, модуль которой равен силе тока через единичную площадку, перпендикулярную направлению движения зарядов в данной точке проводника, а направление совпадает с направлением движения зарядов. : 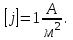 § 2. Закон Ома для однородного участка цепи На основании многочисленных экспериментальных данных немецкий физик Георг Ом установил, что ток, протекающий по проводнику, пропорционален разности потенциалов  – напряжению, приложенному к проводнику: – напряжению, приложенному к проводнику: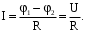 (6.5) (6.5)Формула (6.5) выражает закон Ома для однородного участка цепи. Коэффициент R – электрическое сопротивление проводника или просто сопротивление.  Сопротивление Сопротивление проводника зависит от размеров проводника, его формы, материала проводника. 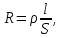 (6.6) (6.6) – удельное сопротивление проводника, коэффициент, характеризующий свойства материал, из которого сделан проводник. Удельное сопротивление – одна из основных электрических характеристик материала проводника, имеются справочные данные на все электротехнические материалы. Единица измерения удельного сопротивления в системе СИ – Омм. Это сопротивление куба с длиной ребра 1 м. § 3. Закон Ома в дифференциальной форме 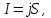 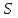 – поперечное сечение проводника, – поперечное сечение проводника, 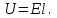 Подставляя эти соотношения в формулу закона Ома (6.5), получаем: 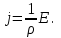 § 5. Электродвижущая сила Электродвижущей силой источника (ЭДС) называется отношение работы сторонних сил по перемещению заряда q к величине перемещенного заряда: 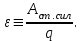 (6.11) (6.11)Ясно, что ЭДС измеряется в тех же единицах, что и потенциал (3.5) – в вольтах. Второй характеристикой источника тока является внутреннее сопротивление. Под действием сторонних сил свободные заряды участвуют в упорядоченном движении так же, как и под действием сил в электрическом поле, их движение можно охарактеризовать сопротивлением, как и движение зарядов под действием электрического поля. Это сопротивление называют внутренним. § 5. Работа электрического тока. Закон Джоуля-Ленца Если по проводнику течет ток силой I, то, в соответствии с (6.1), за время dt через сечение проводника пройдет заряд: 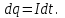 получаем формулы для количества тепла dQ и мощности P:  (7.3) (7.3) (7.4) (7.4)Формулу (7.3) называют законом Джоуля-Ленца. Количество тепла в системе СИ измеряют в джоулях, но часто используется и внесистемная единица – калория. Если измерять тепло в калориях, в формуле (7.3) появляется переводной коэффициент, равный значению 1 Дж в калориях – 0,24 (кал/Дж):  , (кал) (7.3а) , (кал) (7.3а)Этот закон определяет количество тепла, выделяющееся в единичном объеме проводника в единицу времени – удельную тепловую мощность тока w: 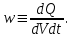 (7.5) (7.5)мощность, выделяемая в единице объема проводника, удельная тепловая мощность тока, равна: 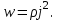 (7.7) (7.7)эквивалентные выражения закона Джоуля-Ленца в дифференциальной форме: 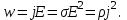 (7.8) (7.8)Для количества тепла dQ, выделяющегося в объеме dV за время dt, из (7.8) получаем: 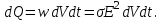 (7.9) (7.9)МАГНЕТИЗМ ЛЕКЦИЯ № 4 Магнитное поле. Вектор магнитной индукции. Закон Био-Савара-Лапласа § 1. Магнитное поле Движущийся заряд является источником магнитного поля; магнитное поле оказывает силовое воздействие на другой движущийся в нем заряд. В опытах Эрстеда при изменении направления тока стрелка отклонялась в противоположную сторону – значит магнитное поле характеризуется векторной величиной. Силовую характеристику магнитного поля В называют вектором магнитной индукции, хотя по аналогии с электрическим полем следовало бы назвать напряженностью магнитного поля. Но исторически сложилось так, что напряженностью называют вспомогательную характеристику магнитного поля. Аналогично в случае магнитного поля можно показать, что на рамку с током в магнитном поле действует механический момент сил.  Маленькая рамка с током по отношению к вектору магнитной индукции В выполняет такую же роль, как точечный заряд по отношению к вектору напряженности электрического поля Е: рамка с током позволяет определить среднюю величину и направление вектора магнитной индукции В в области пространства, сравнимой с размерами рамки. Если рамку с током к тому же сделать очень маленькой, то можно сказать, что с ее помощью можно определить величину и направление магнитного поля в каждой точке пространства. Маленькая рамка с током по отношению к вектору магнитной индукции В выполняет такую же роль, как точечный заряд по отношению к вектору напряженности электрического поля Е: рамка с током позволяет определить среднюю величину и направление вектора магнитной индукции В в области пространства, сравнимой с размерами рамки. Если рамку с током к тому же сделать очень маленькой, то можно сказать, что с ее помощью можно определить величину и направление магнитного поля в каждой точке пространства. Модуль вектора магнитной индукции пропорционален максимальному вращающему моменту:  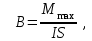 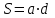 . . |


 ,
,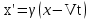 ,
,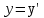 ,
,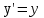 ,
,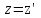 ,
, 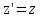 ,
,  ;
; .
.