Физика. Лекции. Лекция1 Предмет механики
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
|
ЛЕКЦИЯ№1 Предмет механики Механика изучает изменение с течением времени взаимного положения материальных тел в пространстве и происходящие при этом взаимодействия между ними. Классическая механика справедлива для любых тел, кроме элементарных частиц. Скорости движения тел должны быть малы по сравнению со скоростью света, с = 3 10 м/с. Релятивистская механика, или специальная теория относительности, справедлива при любых скоростях, в том числе, сравнимых со скоростью света. Согласно специальной теории относительности, скорости тел не могут превышать скорость света. Квантовая механика изучает движение элементарных частиц. Элементы квантовой механики будут рассмотрены в пятой части настоящего курса лекций. Структура классической механики, ее основная задача Классическая механика делится на кинематику, динамик и статику. Кинематика - раздел механики, изучающий движения тел в пространстве и времени без рассмотрения вызывающих это движение взаимодействий. Динамика изучает движение тел, учитывая взаимодействия между телами, которые обуславливают тот или иной характер движения. Статика изучает законы равновесия системы тел. Эти законы следуют из законов динамики. ЭЛЕМЕНТЫ КИНЕМАТИКИ §1. Простейшие физические модели. Материальная точка Материальная точка - это одна из простейших физических моделей. Абсолютно твердое тело Существуют такие задачи, в которых размерами тела нельзя пренебречь, но в то же время можно не учитывать изменение со временем размеров и формы тела. § 2. Положение материальной точки в пространстве. Тело отсчета - это тело, относительно которого определяют положение рассматриваемого нами тела или системы тел. Система отсчета Это система координат, связанная с телом отсчета и выбранный способ измерения времени (часы). Координаты точкиПервый способ задать положение материальной точки ‑ это задать ее координаты. Например, три числа xА, yА, zА (рис. 1.4) задают положение точки A в декартовой системе координат.   Рис. 1.4Второй способ задать положение точки – задать радиус-вектор. Радиус-вектор – это вектор, проведенный из начала координат (рис. 1.5) в какую-либо точку пространства. Если там находится материальная точка, то мы будем иметь радиус-вектор материальной точки.  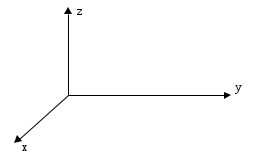 Рис. 1.5 Числа 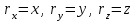 – компоненты радиус-вектора. Очевидно, они же являются координатами материальной точки: – компоненты радиус-вектора. Очевидно, они же являются координатами материальной точки: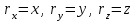 . (1.2) . (1.2)Модуль радиус-вектора – это его длина. 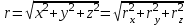 . (1.3) . (1.3)Траектория – это линия, описываемая материальной точкой при ее движении. Путь s – длина пройденного материальной точкой участка траектории. Перемещение – вектор, проведенный из начального положения материальной точки в ее конечное положение: Скорость. Вычисление пройденного пути. Ускорение §3 Скорость – это производная радиус-вектора по времени. 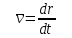 (2.1) (2.1)Как видно из этого определения, скорость – величина векторная, т.е. когда употребляют термин «скорость», имеют в виду вектор, который имеет две характеристики: направление и модуль. Скорость направлена по касательной к траектории. 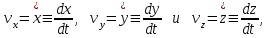 (2.2) (2.2)т.е. компоненты скорости в декартовых координатах равны производным соответствующих координат по времени. Модуль скорости – это производная пути по времени.  . .Для равномерного движения, т.е. для движения с постоянной по модулю скоростью:  , путь равен: , путь равен:  , (2.5) , (2.5)где s12 – весь путь (рис. 2.3);  t – весь отрезок времени;   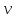 – const. – const.Рис. 2.3 Для произвольного движения (рис. 2.4), т.е. для движения с переменной скоростью разобьем весь путь на очень маленькие участки s:    . .Рис. 2.4 Значения модуля скорости 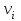 в течение отрезка времени в течение отрезка времени  приблизительно постоянны, если приблизительно постоянны, если  достаточно малы. достаточно малы.В пределе: 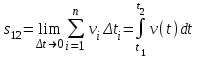 , (2.6) , (2.6)т.е. путь – это определенный интеграл от модуля скорости по времени. Так как модуль скорости – величина положительная, то путь всегда положителен и может только возрастать с течением времени. §5. Ускорение В общем случае скорость материальной точки может изменяться как по величине (т.е. по модулю), так и по направлению. Быстроту этого изменения характеризует векторная величина, которую называют термином «ускорение». Ускорение – это производная скорости по времени. 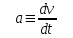 . (2.7) . (2.7)Ускорение – вторая производная радиус-вектора по времени. Производную по времени от какой-либо величины называют скоростью изменения этой величины. Ускорение – это скорость изменения скорости. 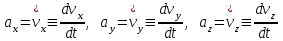 , (2.9) , (2.9)т.е. компоненты ускорения равны производным по времени от соответствующих компонент скорости. Используя формулы (2.8) и (1.1), получим, что:  , (2.9а) , (2.9а)т.е. компоненты ускорения равны вторым производным по времени от соответствующих координат материальной точки. §6. Нормальное и тангенциальное ускорение Пусть материальная точка движется по произвольной криволинейной траектории (рис. 3.1) с переменной по модулю скоростью. В этом случае за счет криволинейности траектории скорость будет изменяться по направлению, кроме того, у скорости изменяется ее модуль. Для характеристики такого движения полное ускорение удобно представить в виде суммы двух составляющих: нормального ускорения, направленного перпендикулярно скорости, и тангенциального ускорения, направленного вдоль вектора скорости. (3.1) нормальное ускорение, 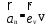 (3.2) (3.2)показывает быстроту изменения направления скорости. Второй член, тангенциальное ускорение, 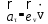 (3.3) (3.3)направлен вдоль скорости и показывает быстроту изменения ее модуля. Модуль тангенциального ускорения равен, как следует из (3.3): 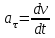 . (3.3а) . (3.3а)Нормальное ускорение направлено по нормали к скорости, его модуль равен: 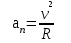 . (3.4а) . (3.4а)Модуль полного ускорения вычисляется по теореме Пифагора: 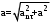 . .ЛЕКЦИЯ №2 Законы Ньютона Основы классической динамики составляют три закона, сформулированные И. Ньютоном в 1687 году. Это фундаментальные законы, они ниоткуда не выводятся и получены на основе осмысливания и обобщения многочисленных опытных данных. Законы Ньютона выполняются только в инерциальных системах отсчета. Инерциальные системы отсчета. Первый закон НьютонаИнерциальная система отсчета – это система отсчета, в которой тела, не подверженные воздействию других тел, движутся прямолинейно и равномерно или покоятся. Первый закон НьютонаВсякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Сила. Масса. ИмпульсСила  – векторная величина, характеризующая воздействие на данное тело других тел. – векторная величина, характеризующая воздействие на данное тело других тел.Величину силы можно определить опытным путем, используя прибор для измерения силы – динамометр. Сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Масса тела, m, – скалярная величина, являющаяся мерой инертности тела. Инертность – неподатливость действию силы, свойство тела сохранять величину и направление своей скорости, невозможность ее мгновенного изменения. Импульс материальной точки – это вектор, равный, в механике Ньютона, произведению массы материальной точки на ее скорость: Второй закон НьютонаСкорость изменения импульса (т.е. производная импульса по времени) равна действующей на материальную точку равнодействующей силе:  , (4.3) , (4.3)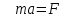 (4.4) (4.4)Третий закон Ньютона Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению. Пример – взаимодействие двух электрических зарядов, изображенных на рис. 4.2. Рис. 4.2 Обратим внимание, что силы, о которых говорится в третьем законе Ньютона, приложены к разным телам (рис. 4.2) и являются силами одной природы. Из третьего закона Ньютона следует, что для каждой силы можно указать тело, являющееся причиной этой силы. Если же указать такое тело – причину возникшей силы – не удается, то тогда причина «силы» – неинерциальность системы отсчета. Напомним, что законы Ньютона справедливы только в инерциальных системах отсчета. §2. Силы в природе Все изучаемое физикой многообразие взаимодействий тел сводится к четырем видам: гравитационному – описываемому законом всемирного тяготения; электромагнитному – взаимодействию заряженных тел и частиц; сильному (ядерному) – обеспечивающему связь частиц в атомном ядре; слабому – ответственному за многие процессы распада элементарных частиц. Сила тяжести и весИсааком Ньютоном был сформулирован фундаментальный закон всемирного тяготения: силы, с которыми две материальные точки притягиваются друг к другу, пропорциональны их массам и обратно пропорциональны квадрату расстояния между ними:  , (4.6) , (4.6)где F – сила; 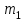 и и  – массы материальных точек; – массы материальных точек; r – расстояние между ними, G = 6,67 × 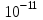 м м /кг с /кг с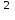 – гравитационная постоянная. – гравитационная постоянная.Сила тяжести равна: 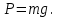 (4.7) (4.7)Вес тела – это сила, с которой тело действует на подвес или опору вследствие гравитационного притяжения к Земле. Вес тела зависит от характера его движения. Если подвес или опора покоятся относительно Земли, то вес и сила тяжести равны друг другу. Если же точка крепления подвеса или опора движется с ускорением, вес перестает быть равным силе тяжести. Силы упругостиУпругие силы возникают в деформированном теле. Они уравновешивают внешние силы, вызвавшие деформацию. Установленный экспериментально закон Гука утверждает, что при деформации тела величина деформации х пропорциональна величине деформирующей силы F. 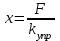 , ,где kупр – коэффициент упругости (жесткости) тела, зависящий от свойств материала, размеров и формы тела и вида деформации. Следовательно, по третьему закону Ньютона, Fупр = ‑F, и для силы упругости имеем: 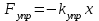 . (4.8) . (4.8)Следовательно, сила упругости направлена в сторону, противоположную абсолютной деформации х, и приложена к телам, вызывающим деформацию. Силы тренияСилы трения возникают при перемещении соприкасающихся тел или их частей друг относительно друга. Трение подразделяется на внешнее и внутреннее. Внутреннее трение в жидкостях и газах называется вязкостью. Внешнее трение возникает при относительном перемещении двух соприкасающихся твердых тел. Опытным путем установлено, что максимальная сила трения покоя не зависит от площади соприкасающихся тел и приблизительно пропорциональна модулю силы нормального давления, прижимающей трущиеся поверхности друг к другу: 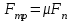 , (4.9) , (4.9)где μ– безразмерный множитель, называемый коэффициентом трения покоя. (он зависит от природы и состояния трущихся поверхностей); 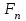 – сила нормального давления (она направлена перпендикулярно трущимся поверхностям). – сила нормального давления (она направлена перпендикулярно трущимся поверхностям).Закон сохранения импульса §4. Роль законов сохранения в механике. Определения необходимых терминов Механическая система ‑ это совокупность тел, выделенных нами для рассмотрения.
|


 Внутренние и внешние силы
Внутренние и внешние силы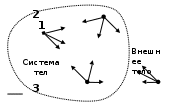 Внутренние силы – это силы, с которыми взаимодействуют тела системы между собой.
Внутренние силы – это силы, с которыми взаимодействуют тела системы между собой.
 . (5.1)
. (5.1)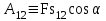 . (5.3)
. (5.3) . (5.4)
. (5.4)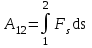
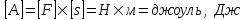 .
.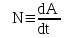 . (5.6)
. (5.6)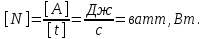
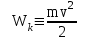 . (5.9)
. (5.9)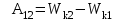 . (5.11)
. (5.11)


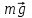
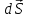
 Силы, не обладающие только что названным свойством, называют неконсервативными.
Силы, не обладающие только что названным свойством, называют неконсервативными.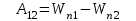 , (6.2)
, (6.2)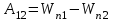
 из записанных выше выражений, получим:
из записанных выше выражений, получим: или
или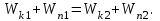 (6.7)
(6.7) (6.8)
(6.8) . (6.9)
. (6.9)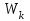 – кинетическая энергия системы;
– кинетическая энергия системы;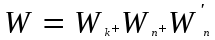 , (6.10)
, (6.10)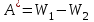 , (6.11)
, (6.11)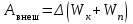 . 6.12)
. 6.12)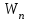 – потенциальная энергия во внешнем поле. Если Авнеш > 0, то
– потенциальная энергия во внешнем поле. Если Авнеш > 0, то