Физика. Лекции. Лекция1 Предмет механики
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
§ 5. Основное уравнение молекулярно-кинетическойтеории идеального газаосновное уравнение молекулярно-кинетической теории идеального газа: 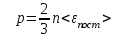 , (1.7) , (1.7)здесь 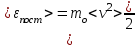 – средняя кинетическая энергия поступательного движения одной молекулы. – средняя кинетическая энергия поступательного движения одной молекулы.§ 6. Молекулярно-кинетический смысл температуры.Средняя энергия одной молекулы Запишем рядом два уравнения: уравнение состояния идеального газа в форме, полученной в § 4 и основное уравнение молекулярно-кинетической теории: 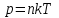 см. (1.5), см. (1.5),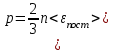 см. (1.7). см. (1.7).Приравнивая правые части, получим: 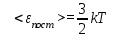 . (1.8) . (1.8)Таким образом молекулярно-кинетическая теория раскрывает физический смысл абсолютной температуры (молекулярно-кинетический смысл температуры): T – это величина, пропорциональная средней энергии поступательного движения одной (!) молекулы.  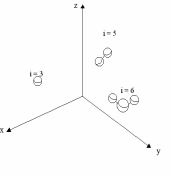 Рисунок 1 Число степеней свободы механической системы – это минимальное число независимых координат, которые полностью определяют пространственное положение рассматриваемой системы. В частности, можно говорить и о числе степеней свободы молекулы. Обозначается число степеней свободы буквой i (рис. 1.5). Для материальной точки это число равно трем, так как ее положение полностью определяется тремя координатами x, y, z. Материальная точка используется в качестве модели одноатомной молекулы идеального газа, таким образом, Рис. 1.5 для нее i = 3. ЛЕКЦИЯ № 2 В общем случае для описания движения микрочастиц необходимо применять законы квантовой механики. Статистическая физика, описывающая макросистемы, состоящие из микрочастиц, движение которых описывается законами квантовой механики, называется квантовой статистикой. Основы квантовой статистики будут даны в этих лекциях после изложения раздела «Квантовая физика». Одним из основных понятий статистики (как классической, так и квантовой) является вероятность. Вероятность wi того, что величина х имеет значение хi, называется пределом отношения числа Ni к полному числу измерений N при стремлении N к 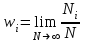 . . Распределение Больцмана Воспользовавшись соотношением p = nkT и независимостью температуры Т от z, можно получить: 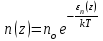 . . 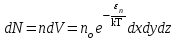 . .А вероятность нахождения в этом объеме будет 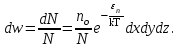 Это полученное Больцманом соотношение называется распределением Больцмана. § 1. Распределение Максвелла 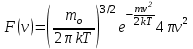 . (3.4) . (3.4)Полученную Д.К. Максвеллом функцию F(v) принято называть функцией распределения вероятностей, или функцией распределения Максвелла. Г 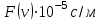 рафик функции распределения Максвелла приведен на рис. 3.2. рафик функции распределения Максвелла приведен на рис. 3.2.     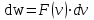 Рис.3.2 При v = 0 множитель v2 функции F(v) обращает ее в ноль. При v > 0 функция F(v) сначала растет за счет множителя v2, а затем при v быстро стремится к нулю за счет экспоненциального множителя. § 3. Наиболее вероятная, средняя и средняя квадратичная скорости молекул Наиболее вероятной скоростью молекул идеального газа, находящегося в термодинамическом равновесии, называют (что следует из физического смысла F(v)) скорость, при которой функция F(v) достигает максимального значения. 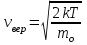 . (3.9) . (3.9) . (3.11) . (3.11)Средняя квадратичная скорость vср.кв. характеризует среднюю энергию поступательного движения молекулы. По определению: 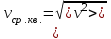 . (3.12) . (3.12)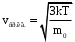 . (3.13) . (3.13)Отсюда средняя кинетическая энергия поступательного движения одной молекулы: 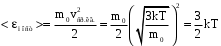 . . ЛЕКЦИЯ № 3 § 1. Основные понятия термодинамики Термодинамическая система – это совокупность макроскопических тел, которые могут взаимодействовать между собой и с другими телами (внешней средой) – обмениваться с ними энергией и веществом. В частности, термодинамическая система может состоять из одного макроскопического тела. В некоторых отношениях простейшим макроскопическим телом является идеальный газ, на примере которого мы будем иллюстрировать понятия и законы термодинамики. Состояние термодинамической системы характеризуют макроскопическими параметрами состояния: давлением, температурой, объемом, плотностью и т. д. Например, для заданной массы идеального газа параметрами состояния являются три величины: p, V, T. Равновесное состояние – это такое состояние системы, в которое она самопроизвольно переходит через достаточно большой промежуток времени (время релаксации) в условиях изоляции от окружающей среды. В равновесном состоянии параметры системы имеют определенные значения и не меняются со временем. Термодинамическим процессом называется всякое изменение во времени хотя бы одного из параметров состояния системы. Равновесным термодинамическим процессом называют процесс, состоящий из непрерывной последовательности равновесных состояний. Строго равновесным может быть только бесконечно медленный процесс. Равновесный процесс является обратимым, так как он может быть осуществлен в обратном направлении через те же промежуточные состояния и без каких-либо изменений в окружающих телах. Классическая термодинамика дает полное количественное описание только равновесных процессов. Термодинамика неравновесных процессов занимается изучением количественных закономерностей в неравновесных процессах для состояний, не сильно отличающихся от равновесных. § 2. Первое начало термодинамики Первое начало термодинамики – это закон сохранения энергии для систем, в которых существенную роль играют тепловые процессы. Важнейшей характеристикой такой системы является ее внутренняя энергия. Внутренняя энергия термодинамической системы U– это энергия физической системы, зависящая от ее внутреннего состояния. Внутренняя энергия включает в себя энергию хаотического (теплового) движения всех микрочастиц системы и энергию взаимодействия этих частиц между собой. Во внутреннюю энергию не входит кинетическая энергия движения системы как целого и ее потенциальная энергия во внешних полях. Внутренняя энергия – функция состояния системы, т. е. величина внутренней энергии не зависит от процесса перехода системы в данное состояние, а определяется значением параметров состояния. В идеальном газе молекулы не взаимодействуют между собой, поэтому его внутренняя энергия: 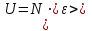 , (4.1) , (4.1)где N – число молекул в рассматриваемом количестве газа, которое, согласно (1.3), равно 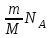 ; <> – средняя энергия одной молекулы, которая, согласно (1.9) равна ; <> – средняя энергия одной молекулы, которая, согласно (1.9) равна 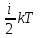 . .Отсюда внутренняя энергия идеального газа: 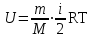 . . Теплота Q, сообщенная телу, есть не что иное, как количество энергии, сообщенное телу за счет обмена энергиями между молекулами контактирующих тел. В общем случае количество тепла, сообщенное термодинамической системе, идет на приращение внутренней энергии системы и на совершение работы над внешними телами, т. е.: 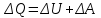 . (4.3) . (4.3)Это и есть первое начало термодинамики § 3. Теплоемкость идеального газа Теплоемкость тела – это отношение тепла, сообщенного телу, к изменению температуры Т, которое при этом произошло: 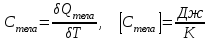 . (4.7) . (4.7)Удельная теплоемкость – это отношение теплоемкости тела к его массе, т. е.: 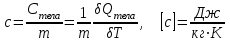 . (4.8) . (4.8)Молярная теплоемкость – это теплоемкость одного моля вещества, т. е.: 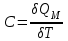 . (4.9) . (4.9)Здесь QМ – количество тепла, подведенное к одному молю вещества для нагревания его на Т. Так как масса одного моля равна М, из (4.8) можно получить связь между С и с: 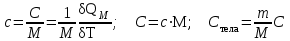 . (4.10) . (4.10)Определим молярную теплоемкость идеального газа при постоянном объеме. Согласно первому началу термодинамики: 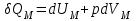 . .Определим молярную теплоемкость идеального газа при постоянном давлении: 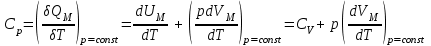 . .Отношение теплоемкостей 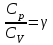 называют коэффициентом Пуассона. называют коэффициентом Пуассона. 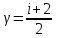 . . § 4. Изопроцессы Изопроцессами называются равновесные процессы, при которых один из параметров состояния (р, V или Т) остается постоянным. Изохорическим процессом называется процесс, когда V = const или, как это следует из уравнения состояния идеального газа (1.2): 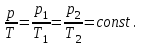 Фактически мы уже занимались исследованием изохорического процесса, определяя CV в предыдущем параграфе. Итак, для изохорического процесса выполняются следующие соотношения: 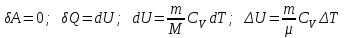 . (4.16) . (4.16)Изобарическим процессом называется процесс, в котором p = const или, как это следует из уравнения состояния идеального газа (1.2): 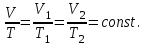 Диаграмма этого изопроцесса в координатах p, V изображена на рис. 4.4. Работа при изобарическом расширении: 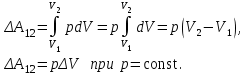 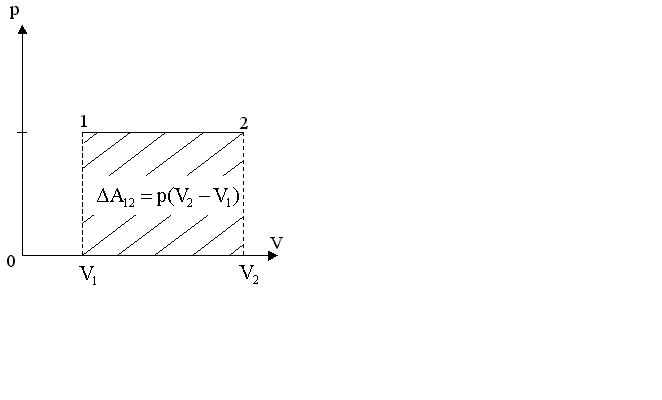 Из уравнения Клапейрона – Менделеева (1.2) при p = const следует: 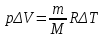 . .Отсюда и из (4.16): 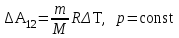 . .Исследованием изобарического процесса мы фактически занимались в предыдущем параграфе, где была определена теплоемкость при постоянном давлении. Из (4.10) и (4.7) следует: 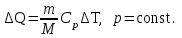 Приращение внутренней энергии здесь по-прежнему определяется формулой: 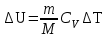 . .Изотермическим процессом называется процесс при T = const или, как это следует из уравнения состояния идеального газа: 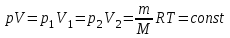 . (4.17) . (4.17)В координатах p, V диаграмма этого процесса – гипербола (рис. 4.5). Работа при изотермическом расширении: 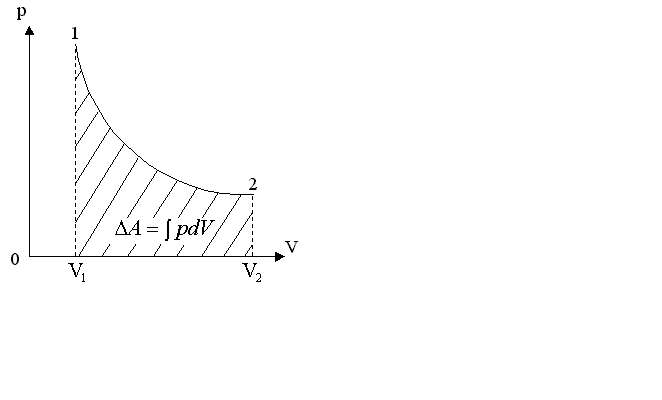 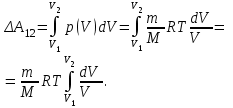 После интегрирования получим:  Рис. 4.5 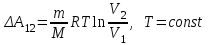 .(4.18) .(4.18) При T = const внутренняя энергия идеального газа (4.12) не изменяется, поэтому dU = 0. Отсюда и из первого начала термодинамики: 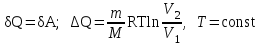 . .§ 5. Адиабатический процесс Адиабатическим называется процесс, идущий без теплообмена с окружающей средой. Исключить теплообмен можно либо за счет хорошей теплоизоляции, либо за счет очень короткого времени протекания процесса (быстропротекающий процесс). Выведем уравнение адиабаты. Для этого при Q = 0 из первого начала термодинамики (4.6), имеем: 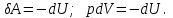 Откуда и из (4.12) получаем: 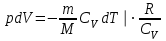 . .Продифференцировав уравнение Клапейрона – Меделеева (1.2), получим: 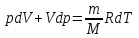 . .Сложим полученное выражение с предыдущим, умноженным на 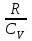 , , и получим: 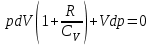 . (4.19) . (4.19)Поскольку 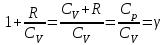 , ,уравнение (5.1) принимает вид: 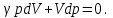 Или после деления на pV: 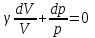 . .После интегрирования получаем: 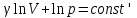 или после простейших преобразований: 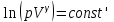 . .Если логарифм некоторой величины есть константа, то константой, но уже другой, является и сама эта величина: 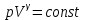 . (4.20) . (4.20)Выражение (4.20) и есть уравнение адиабаты в координатах р, V. Его называют также уравнением Пуассона, а отношение теплоемкостей 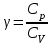 – коэффициентом Пуассона. – коэффициентом Пуассона. |
