Физика. Лекции. Лекция1 Предмет механики
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
E2
NA), заданное с помощью макроскопических величин, характеризующих все тело в целом. Такими величинами могут быть давление p, объем V, температура T, внутренняя энергия U. |
Задать микросостояние – это значит задать состояния всех частиц, из которых состоит макроскопическое тело.
В классической механике состояние материальной точки считается заданным, если задан ее радиус-вектор
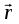 и вектор ее скорости
и вектор ее скорости  . Величины
. Величины 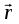 и
и  изменяются с течением времени непрерывно, поэтому в рамках классической механики нельзя ввести понятие «число состояний, в которых может находиться частица». Такая возможность появляется при описании микрочастиц на более глубоком, квантовом уровне, где величины, характеризующие состояние микрочастиц изменяются скачкообразно, дискретно.
изменяются с течением времени непрерывно, поэтому в рамках классической механики нельзя ввести понятие «число состояний, в которых может находиться частица». Такая возможность появляется при описании микрочастиц на более глубоком, квантовом уровне, где величины, характеризующие состояние микрочастиц изменяются скачкообразно, дискретно.Статистический вес (статвес) – это число различных микросостояний, соответствующих данному макросостоянию.
Мы будем обозначать статвес греческой буквой .
Равновесным называется такое макроскопическое состояние системы, которое не имеет тенденции к изменению с течением времени. Ясно, что равновесное макросостояние – это такое состояние, которое реализуется наибольшим числом микросостояний, т. е. статвес равновесного состояния максимален.
Неравновесные состояния – это состояния со статвесом меньшим, чем
у равновесного. В неравновесном состоянии система находится тем меньше, чем меньше его статвес.
Необратимым называется процесс, обратный которому маловероятен.
Если собрать все молекулы в одной половине сосуда и убрать перегородку, то газ распространится на весь сосуд. Вероятность того, что он вновь соберется в одной половине сосуда, как мы подсчитали в конце раздела предыдущего параграфа, изчезающе мала, можно считать, что такой процесс никогда не произойдет.
свойства энтропии определяются свойствами макросостояния:
1) энтропия изолированной системы возрастает при протекании необратимого процесса (так как при этом возрастает статвес макросостояния);
2) энтропия системы, находящейся в равновесном состоянии, максимальна (это свойство энтропии также связано со статвесом, который максимален
в равновесном состоянии).
Второе начало термодинамики утверждает, что энтропия изолированной системы не может убывать.
Второе начало термодинамики называется законом возрастания энтропии.
Энтропия и количество тепла, получаемое системой, связаны между собой.
Можно показать, что если система получает в обратимом процессе количество тепла Q при температуре T, то ее энтропия возрастает на величину
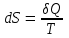 (для обратимого процесса). (5.3)
(для обратимого процесса). (5.3) Для необратимого процесса энтропия возрастает и за счет необратимости и, если система получает количество тепла Q при температуре T, то тогда
 (для необратимого процесса).
(для необратимого процесса).Связаны между собой также энтропия и беспорядок.
Упорядоченным называют состояние, осуществляемое малым числом способов, т. е. у упорядоченного состояния статвес (5.2) мал, значит, мала и энтропия (5.1).
Беспорядочное, или случайное, состояние – это состояние, которое может реализовываться большим числом способов.
Третье начало термодинамики
При абсолютном нуле все квантовые системы переходят в основное состояние. Если оно единственное, то его статвес равен единице и энтропия
S = k ln 1 = 0.
Значит, энтропия всякого тела стремится к нулю при стремлении к нулю абсолютной температуры, т. е.
 (5.4)
(5.4)Это утверждение называется третьим началом термодинамики, или теоремой Нернста.
§ 4. Энтропия идеального газа
Для обратимого процесса
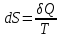 , см (5.3).
, см (5.3).Из первого начала термодинамики (4.6), примененного к идеальному газу (4.12), следует, что:
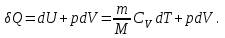
Объединяя эти равенства, получим:
 . (5.5)
. (5.5)Заменим
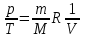 (см. (1.2), уравнение Клапейрона – Менделеева).
(см. (1.2), уравнение Клапейрона – Менделеева).Тогда
 .
.После интегрирования получим:
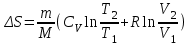 .
. Лекция 1
1. Немецкий физик Макс Планк в 1900 г. выдвинул гипотезу, согласно которой электромагнитная энергия излучается порциями, квантами энергии. Величина кванта энергии (см. (1.2):
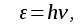
где h = 6,6261·10-34 Дж · с – постоянная Планка; – частота колебаний электромагнитной волны, излучаемой телом.
Эта гипотеза позволила Планку решить проблему излучения абсолютно черного тела. Проблема излучения абсолютно черного тела состояла в том, чтобы теоретически получить зависимость спектральной плотности энергетической светимости абсолютно черного тела от длины волны излучения и температуры излучающего тела.
2. Фотоэффект – это испускание электронов веществом под действием электромагнитного излучения.
3. Экспериментальные исследования фотоэффекта, проведенные в 1900 – 1904 гг., показали следующее:
1) энергия вылетевших из фотокатода электронов не зависит от интенсивности света;
2) эта энергия прямо пропорциональна частоте света, освещающего фотокатод.

4. Проблема фотоэффектасостояла в том, что теоретические предсказания, сделанные для фотоэффекта на основе электродинамики Максвелла, противоречили результатам опытов. Теория Максвелла предсказывала, что энергия, передаваемая световой волной электрону, должна быть пропорциональна интенсивности света. Кроме того, в классической электродинамике нет никаких объяснений прямой пропорциональности кинетической энергии электронов
 частоте света .
частоте света .5. Проблема фотоэффекта была разрешена в 1905 г. А. Эйнштейном, который предположил, что свет состоит из потока квантов (фотонов) с энергией (см. (3.2)):

6. Применив к процессу поглощения фотона закон сохранения энергии, Эйнштейн получил следующее уравнение для фотоэффекта (см. (3.3)):
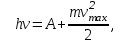
здесь А – работа выхода электрона из вещества; m – масса электрона;
vmax – его скорость в момент вылета из фотокатода.
7. Из уравнения Эйнштейна для фотоэффекта следует, что если энергия фотона h меньше работы выхода А, то фотоэффект невозможен. Граничная частота называется красной границей фотоэффекта и определяется равенством (см. (3.5)):



i

Лекция 2
1. Уравнение движения электрона в планетарной модели атома, записанное на основе второго закона Ньютона, позволяет атому иметь любой размер, опыт же показывает, что размеры атомов порядка 10-10 м. Это противоречие теории
и опыта получило название проблемы размера атома.
2. Проблема стабильности атомасостояла в том, что в планетарной модели атома электрон, двигаясь по окружности, должен, из-за наличия ускорения, непрерывно излучать энергию и через время

 , (5.1)
, (5.1)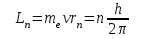 или
или 
 при переходе электрона из одного стационарного состояния в другое. Энергия кванта равна разности энергий стационарных состояний атома, между которыми происходит переход:
при переходе электрона из одного стационарного состояния в другое. Энергия кванта равна разности энергий стационарных состояний атома, между которыми происходит переход:
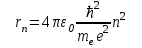
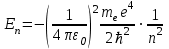 .
.
 ;
;



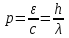 .
.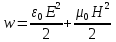
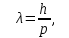
 ,
,
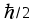 , т. е.
, т. е.